[논문리뷰] Scaling Rectified Flow Transformers for High-Resolution Image Synthesis (Stable Diffusion 3)

ICML 2024. [Paper] [Page]
Patrick Esser, Sumith Kulal, Andreas Blattmann, Rahim Entezari, Jonas Müller, Harry Saini, Yam Levi, Dominik Lorenz, Axel Sauer, Frederic Boesel, Dustin Podell, Tim Dockhorn, Zion English, Kyle Lacey, Alex Goodwin, Yannik Marek, Robin Rombach
Stability AI
5 Mar 2024

Introduction

최근 몇 년 동안 diffusion model은 인상적인 일반화 능력을 갖추고 텍스트 입력에서 고해상도 이미지와 동영상을 생성하는 사실상의 접근 방식이 되었다. 반복적인 특성과 관련된 계산 비용, inference 중 긴 샘플링 시간으로 인해 diffusion model의 보다 효율적인 학습 및 더 빠른 샘플링을 위한 연구가 증가했다.

데이터에서 noise로의 forward 경로를 지정하면 효율적인 학습이 가능하지만, 어떤 경로를 선택해야 할지에 대한 의문도 제기된다. 이러한 선택은 샘플링에 중요한 영향을 미칠 수 있다. 예를 들어, 데이터에서 모든 noise를 제거하지 못하는 forward process는 학습 분포와 테스트 분포의 불일치를 초래하고 아티팩트를 생성할 수 있다. 중요한 점은 forward process의 선택이 학습된 backward process와 샘플링 효율성에도 영향을 미친다는 것이다. 곡선 경로는 프로세스를 시뮬레이션하기 위해 많은 step이 필요한 반면, 직선 경로는 하나의 step으로 시뮬레이션할 수 있으며 오차가 누적될 가능성이 적다. 각 step은 신경망 평가에 해당하므로 샘플링 속도에 직접적인 영향을 미친다.

본 논문은 forward 경로로 데이터와 noise를 직선으로 연결하는 Rectified Flow를 선택하였다. 이 rectified flow는 더 나은 이론적 속성을 가지고 있지만 아직 명확하게 확립되지 않았다. 지금까지 소규모 실험에서 몇 가지 장점이 경험적으로 입증되었지만 이는 대부분 클래스 조건부 모델에 국한되었다. 본 논문에서는 noise를 예측하는 diffusion model과 유사하게 rectified flow 모델에서 noise scale의 가중치를 재조정하였다. 대규모 연구를 통해 새로운 공식을 기존 diffusion model과 비교하고 그 이점을 보여주었다.

저자들은 고정된 텍스트 표현을 cross-attention을 통해 모델에 직접 공급하는 text-to-image 합성에 널리 사용되는 접근 방식이 이상적이지 않다는 것을 보여주고, 이미지와 텍스트 토큰 모두에 대한 학습 가능한 스트림을 통합하는 새로운 아키텍처를 제시하여 두 토큰 간의 양방향 정보 흐름을 가능하게 한다. 저자들은 이것을 개선된 rectified flow 공식과 결합하여 확장성을 조사하였으며, 예측 가능한 확장 추세가 있음을 보여주었다.

Simulation-Free Training of Flows

저자들은 noise 분포 $p_1$의 샘플 $x_1$과 데이터 분포 $p_0$의 샘플 $x_0$ 사이의 매핑을 상미분 방정식(ODE)에 따라 정의하는 생성 모델을 고려하였다.

\[\begin{equation} dy_t = v_\Theta (y_t, t) dt \end{equation}\]

그러나 이 식을 ODE solver로 풀면 특히 대규모 네트워크 아키텍처를 사용하는 경우 계산 비용이 많이 든다. 더 효율적인 대안은 $p_0$와 $p_1$ 사이의 확률 경로를 생성하는 벡터장 $u_t$를 직접 회귀시키는 것이다. 이러한 $u_t$를 구성하기 위해 $p_0$와 $p_1 = \mathcal{N}(0,I)$ 사이의 확률 경로 $p_t$에 해당하는 forward process를 다음과 같이 정의한다.

\[\begin{equation} z_t = a_t x_0 + b_t \epsilon \quad \textrm{where} \; \epsilon \sim \mathcal{N} (0,I) \end{equation}\]

$a_0 = 1$, $b_0 = 0$, $a_1 = 0$, $b_1 = 1$인 경우, marginal

\[\begin{equation} p_t (z_t) = \mathbb{E}_{\epsilon \sim \mathcal{N}(0,I)} p_t (z_t \vert \epsilon) \end{equation}\]

은 데이터 분포와 noise 분포 모두에서 일치한다.

$z_t$, $x_0$, $\epsilon$ 사이의 관계를 표현하기 위해 $\psi_t$와 $u_t$를 다음과 같이 도입한다.

\[\begin{aligned} \psi_t (\cdot \vert \epsilon) &= x_0 \mapsto a_t x_0 + b_t \epsilon \\ u_t (z_t \vert \epsilon) &= \psi_t^\prime (\psi_t^{-1} (z \vert \epsilon) \vert \epsilon) \end{aligned}\]

$z_t$는 초기값이 $z_0 = x_0$인 ODE $z_t^\prime = u_t (z_t \vert \epsilon)$에 대한 해이므로 $u_t(\cdot \vert \epsilon)$는 $p_t (\cdot \vert \epsilon)$을 생성한다. 주목할 점은 조건부 벡터장 $u_t(\cdot \vert \epsilon)$을 사용하여 marginal 확률 경로 $p_t$를 생성하는 marginal 벡터장 $u_t$를 구성할 수 있다는 것이다.

\[\begin{equation} u_t (z) = \mathbb{E}_{\epsilon \sim \mathcal{N}(0,I)} u_t (z \vert \epsilon) \frac{p_t (z \vert \epsilon)}{p_t (z)} \end{equation}\]

위 식의 marginalization으로 인해 Flow Matching 목적 함수

\[\begin{equation} \mathcal{L}_\textrm{FM} = \mathbb{E}_{t, p_t (z)} \| v_\Theta (z, t) - u_t (z) \|_2^2 \end{equation}\]

를 사용하여 $u_t$를 직접 회귀시키는 것은 어려운 반면, 조건부 벡터장 $u_t(z \vert \epsilon)$을 사용하는 Conditional Flow Matching

\[\begin{equation} \mathcal{L}_\textrm{CFM} = \mathbb{E}_{t, p_t (z \vert \epsilon), p_t (z)} \| v_\Theta (z, t) - u_t (z \vert \epsilon) \|_2^2 \end{equation}\]

은 동등하면서도 다루기 쉬운 목적 함수를 제공한다.

Loss를 명시적인 형태로 변환하기 위해

\[\begin{aligned} \psi_t^\prime (x_0 \vert \epsilon) &= a_t^\prime x_0 + b_t^\prime \epsilon \\ \psi_t^{-1} (z \vert \epsilon) &= \frac{z - b_t \epsilon}{a_t} \end{aligned}\]

를 \(u_t (z \vert \epsilon) = \psi_t^\prime (\psi_t^{-1} (z \vert \epsilon) \vert \epsilon)\)에 대입한다.

\[\begin{equation} z_t^\prime = u_t (z_t \vert \epsilon) = \frac{a_t^\prime}{a_t} z_t - \epsilon b_t \left( \frac{a_t^\prime}{a_t} - \frac{b_t^\prime}{b_t} \right) \end{equation}\]

Signal-to-noise ratio (SNR) \(\lambda_t := \log \frac{a_t^2}{b_t^2}\)을 고려하자. \(\lambda_t^\prime - 2 (\frac{a_t^\prime}{a_t} - \frac{b_t^\prime}{b_t})\)을 위 식에 대입한다.

\[\begin{equation} u_t (z_t \vert \epsilon) = \frac{a_t^\prime}{a_t} z_t - \frac{b_t}{2} \lambda_t^\prime \epsilon \end{equation}\]

그런 다음, \(\mathcal{L}_\textrm{CFM}\)을 noise 예측 목적 함수로 reparameterize하기 위해 위 식을 사용한다.

\[\begin{aligned} \mathcal{L}_\textrm{CFM} &= \mathbb{E}_{t, p_t (z \vert \epsilon), p_t (z)} \| v_\Theta (z, t) - \frac{a_t^\prime}{a_t} z + \frac{b_t}{2} \lambda_t^\prime \epsilon \|_2^2 \\ &= \mathbb{E}_{t, p_t (z \vert \epsilon), p_t (z)} \left(-\frac{b_t}{2} \lambda_t^\prime \right)^2 \| \epsilon_\Theta (z, t) - \epsilon \|_2^2 \end{aligned}\]

여기서 \(\epsilon_\Theta = \frac{-2}{\lambda_t^\prime b_t} (v_\Theta - \frac{a_t^\prime}{a_t} z)\)이다.

위 loss의 최적값은 시간에 의존하는 가중치를 도입할 때 변경되지 않는다. 따라서 최적화 경로에 영향을 줄 수 있는 다양한 가중치를 loss function에 도입할 수 있다.

\[\begin{equation} \mathcal{L}_w (x_0) = -\frac{1}{2} \mathbb{E}_{t \sim \mathcal{U}(t), \epsilon \sim \mathcal{N}(0,I)} [w_t \lambda_t^\prime \| \epsilon_\Theta (z_t, t) - \epsilon \|^2] \\ \textrm{where} \; w_t = -\frac{1}{2} \lambda_t^\prime b_t^2 \end{equation}\]

Flow Trajectories

저자들은 위의 식에 대한 다양한 변형을 고려하였다.

Rectified Flow

Rectified Flow (RF)는 데이터 분포와 정규 분포 사이의 직선 경로로 forward process를 정의한다.

\[\begin{equation} z_t = (1 - t) x_0 + t \epsilon \end{equation}\]

\(\mathcal{L}_\textrm{CFM}\)을 사용하며, 이는 $w_t = \frac{t}{1-t}$에 해당한다. 네트워크 출력은 $v_\Theta$이다.

EDM

EDM은 다음과 같은 형태의 forward process를 사용한다.

\[\begin{equation} z_t = x_0 + b_t \epsilon, \quad \textrm{where} \; b_t = \exp F_\mathcal{N}^{-1} (t \vert P_m, P_s^2) \end{equation}\]

\(F_\mathcal{N}^{-1}\)은 평균이 $P_m$이고 분산이 $P_s^2$인 정규 분포의 quantile function이다. SNR \(\lambda_t\)의 분포는 다음과 같다.

\[\begin{equation} \lambda_t \sim \mathcal{N} (-2P_m, (2P_s)^2), \quad t \sim \mathcal{U}(0, 1) \end{equation}\]

네트워크는 $\textbf{F}$-prediction을 통해 parameterize되고 loss는 \(\mathcal{L}_{w_t^\textrm{EDM}}\)로 쓸 수 있다.

\[\begin{equation} w_t^\textrm{EDM} = \mathcal{N}(\lambda_t \vert -2 P_m, (2P_s)^2) (e^{-\lambda_t} + 0.5^2) \end{equation}\]

Cosine

Improved DDPM은 다음과 같은 형태의 forward process를 제안했다.

\[\begin{equation} z_t = \cos (\frac{\pi}{2}t) x_0 + \sin (\frac{\pi}{2}t)\epsilon \end{equation}\]

이는 $\epsilon$-prediction loss와 결합하면 가중치는 \(w_t = \textrm{sech}(\frac{\lambda_t}{2})\)이며, $v$-prediction loss와 결합하면 가중치는 \(w_t = \exp(\frac{\lambda_t}{2})\)이다.

(LDM-)Linear

LDM은 DDPM schedule을 수정하여 사용한다. 둘 다 variance preserving schedule, 즉 \(b_t = \sqrt{1 - a_t^2}\)이고, diffusion 계수 \(\beta_t\)에 따라 $a_t$를 다음과 같이 정의한다.

\[\begin{equation} a_t = \left( \prod_{s=0}^t (1 - \beta_s) \right)^{1/2} \end{equation}\]

주어진 경계 값 \(\beta_0\)와 \(\beta_{T-1}\)에 대해, DDPM은

\[\begin{equation} \beta_t = \beta_0 + \frac{t}{T-1}(\beta_{T-1} - \beta_0) \end{equation}\]

를 사용하고, LDM은

\[\begin{equation} \beta_t = \left( \sqrt{\beta_0} + \frac{t}{T-1} (\sqrt{\beta_{T-1}} - \sqrt{\beta_0}) \right)^2 \end{equation}\]

을 사용한다.

1. Tailored SNR Samplers for RF models

RF loss는 $[0, 1]$의 모든 timestep에서 속도 $v_\Theta$를 균일하게 학습시킨다. 그러나 직관적으로 예측해야 하는 속도 $\epsilon − x_0$는 $[0, 1]$의 중간에 있는 $t$에 대해 더 어렵다. $t = 0$의 경우 최적 예측은 $p_1$의 평균이고 $t = 1$의 경우 최적 예측은 $p_0$의 평균이기 때문이다.

일반적으로 $t$에 대한 분포를 uniform distribution $\mathcal{U}(t)$에서 density가 $\pi(t)$인 분포로 변경하는 것은 \(\mathcal{L}_{w_t^\pi}\)와 동일하다.

\[\begin{equation} w_t^\pi = \frac{t}{1-t} \pi (t) \end{equation}\]

따라서 중간 timestep을 더 자주 샘플링하여 더 많은 가중치를 부여하는 것을 목표로 한다.

Logit-Normal Sampling

중간 timestep에 더 많은 가중치를 두는 분포에 대한 한 가지 옵션은 logit-normal distribution이다.

\[\begin{equation} \pi_\textrm{ln} (t; m, s) = \frac{1}{s \sqrt{2 \pi}} \frac{1}{t(1-t)} \exp \left( - \frac{(\log\frac{t}{1-t} - m)^2}{2s^2} \right) \end{equation}\]

$m$은 location 파라미터이고 $s$는 scale 파라미터이다. Location 파라미터가 음수면 timestep이 데이터 $p_0$로 편향되고, 양수면 noise $p_1$으로 편향된다. Scale 파라미터는 분포의 폭을 제어한다.

실제로는 정규 분포 $u \sim \mathcal{N}(u; m, s)$에서 확률 변수 $u$를 샘플링하고 표준 logistic function에 매핑한다.

Mode Sampling with Heavy Tails

Logit-normal density는 항상 끝점 0과 1에서 값이 0이 된다. 이것이 성능에 부정적인 영향을 미치는지를 확인하기 위해, 저자들은 $[0, 1]$에 대해 엄격하게 양의 density를 갖는 timestep 샘플링 분포도 사용하였다. Scale 파라미터가 $s$인 경우, 다음과 같이 정의된다.

\[\begin{equation} \pi_\textrm{mode}(t; s) = \left\vert \frac{d}{dt} f_\textrm{mode}^{-1} (t) \right\vert \\ \textrm{where} \; f_\textrm{mode} (u; s) = 1 - u - s \cdot \left( \cos^2 (\frac{\pi}{2} u) - 1 + u \right) \end{equation}\]

Scale 파라미터 $s$는 샘플링 중에 중간점($s>0$) 또는 끝점($s<0$)이 선호되는 정도를 제어한다. 또한 $s = 0$이면, $\pi_\textrm{mode}(t; s=0) = \mathcal{U}(t)$이다.

CosMap

마지막으로, 저자들은 RF에서 cosine schedule도 고려하였다. 특히, log-snr이 cosine schedule의 log-snr과 일치하는 매핑 $f : u \mapsto f(u) = t$을 찾는다.

\[\begin{equation} 2 \log \frac{\cos (\frac{\pi}{2}u)}{\sin (\frac{\pi}{2}u)} = 2 \log \frac{1 - f(u)}{f(u)} \end{equation}\]

$f$에 대해 풀면 $u \sim \mathcal{U}(u)$에 대해 다음을 얻는다.

\[\begin{equation} t = f(u) = 1 - \frac{1}{\tan (\frac{\pi}{2}u) + 1} \end{equation}\]

따라서 density는 다음과 같다.

\[\begin{equation} \pi_\textrm{CosMap} (t) = \left\vert \frac{d}{dt} f^{-1} (t) \right\vert = \frac{2}{\pi - 2 \pi t + 2 \pi t^2} \end{equation}\]

Text-to-Image Architecture

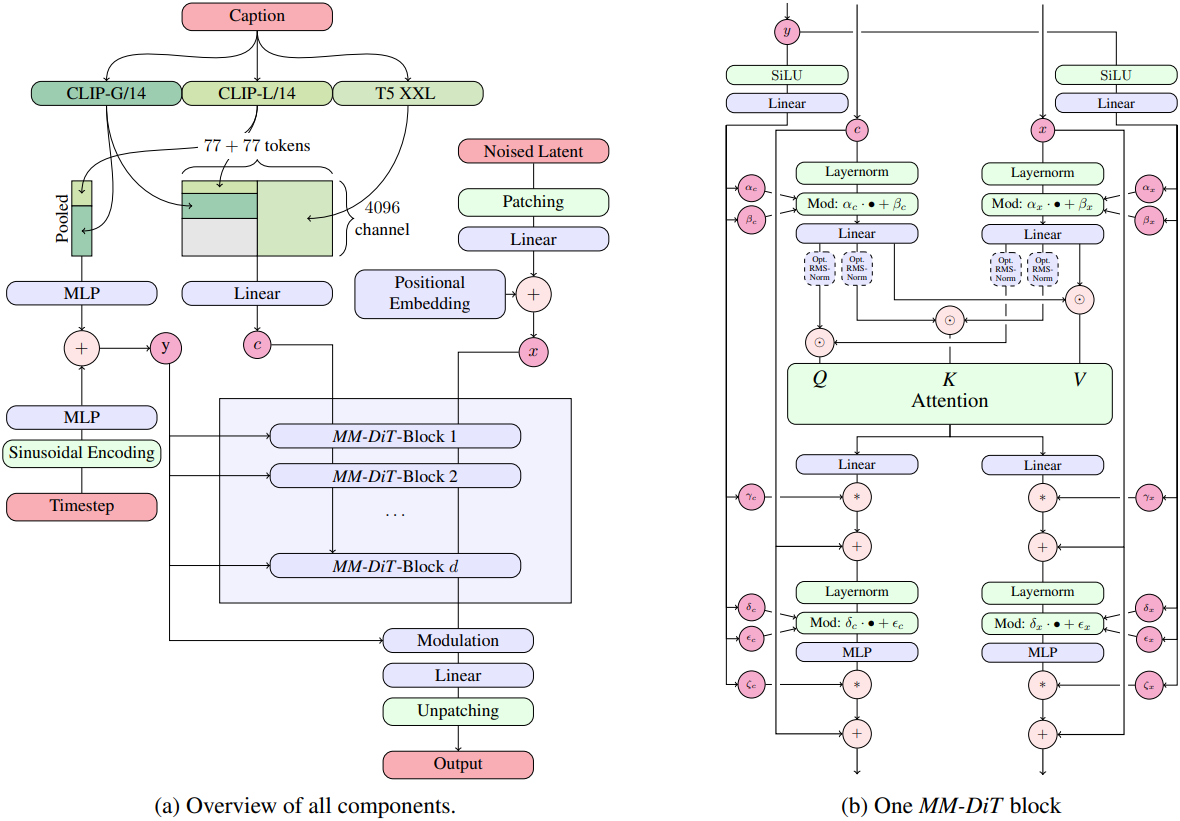
텍스트를 조건으로 이미지를 샘플링 하기 위해, 모델은 텍스트와 이미지라는 두 가지 모달리티를 모두 고려해야 한다. 일반적인 설정은 LDM을 따라 사전 학습된 오토인코더의 latent space에서 text-to-image 모델을 학습시킨다. 텍스트 컨디셔닝 $c$는 사전 학습된 텍스트 모델을 사용하여 인코딩된다.

Multimodal Diffusion Backbone

아키텍처는 DiT를 기반으로 한다. DiT는 클래스 조건부 이미지 생성만을 고려하고 변조 메커니즘을 사용하여 diffusion process의 timestep과 클래스 레이블을 컨디셔닝한다. 이와 마찬가지로 timestep $t$와 \(c_\textrm{vec}\)의 임베딩을 modulation 메커니즘의 입력으로 사용한다. 그러나 pooling된 텍스트 표현은 텍스트 입력에 대한 대략적인 정보만 유지하므로 네트워크는 시퀀스 표현 \(c_\textrm{ctxt}\)의 정보도 필요로 한다.

텍스트와 이미지 입력의 임베딩으로 구성된 시퀀스를 구성한다. 구체적으로, 위치 인코딩을 추가하고 latent 픽셀 표현 $x \in \mathbb{R}^{h \times w \times c}$의 2$\times$2 패치를 길이가 $\frac{hw}{4}$인 패치 인코딩 시퀀스로 flatten한다. 이 패치 인코딩과 텍스트 인코딩 \(c_\textrm{ctxt}\)를 공통 차원에 임베딩한 후, 두 시퀀스를 concat한다. 그런 다음 DiT를 따르고 modulated attention과 MLP의 시퀀스를 적용한다.

텍스트와 이미지 임베딩은 개념적으로 상당히 다르기 때문에 두 모달리티에 대해 각각 별도의 가중치를 사용한다. 이는 각 모달리티에 대해 두 개의 독립적인 transformer를 갖는 것과 동일하지만, attention 연산을 위해 두 모달리티의 시퀀스를 결합하여 두 표현이 각자의 공간에서 작동하면서도 다른 표현을 고려할 수 있도록 한다.

저자들은 스케일링 실험을 위해 모델의 깊이 $d$, 즉 attention block의 수에 따라 모델의 크기를 조절하였다. 이를 위해 hidden size를 $64d$로 설정하고 attention head의 수를 $d$로 설정하였다.

Experiments

1. Improving Rectified Flows

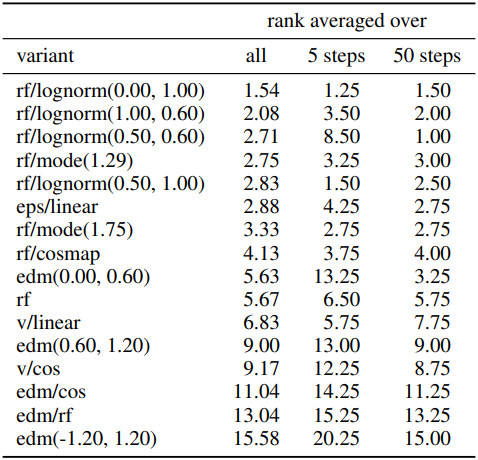
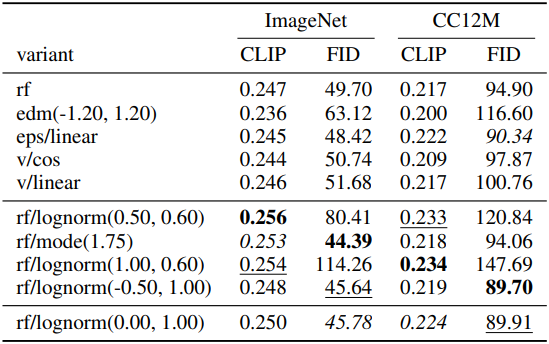
저자들은 61개의 서로 다른 구성을 가진 모델을 학습시켰다. 다음은 학습된 모델들에 대한 (왼쪽) 평균 순위와 (오른쪽) metric을 비교한 표이다.

다음은 샘플링 step 수에 대한 FID를 비교한 그래프이다.

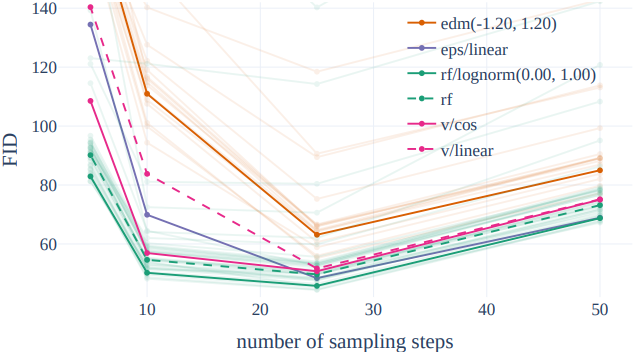
2. Improving Modality Specific Representations

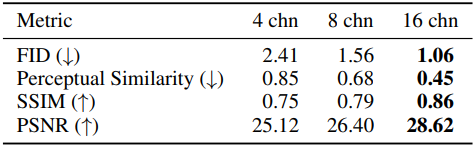
다음은 오토인코더의 채널 수에 대한 ablation 결과이다.

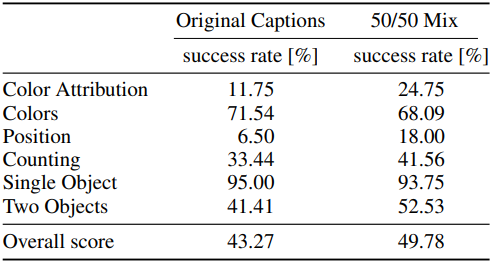
다음은 원래 캡션을 사용하였을 때와 원래 캡션과 CogVLM으로 생성된 캡션을 반반 섞어서 사용하였을 때의 결과이다.

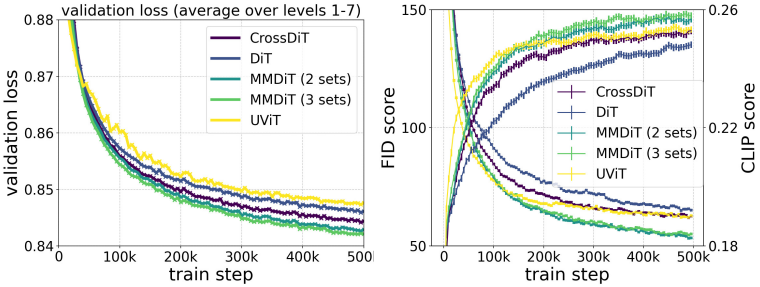
다음은 모델 backbone에 대한 ablation 결과이다. (MM-DiT가 본 논문에서 제안된 아키텍처)

3. Training at Scale

QK 정규화

저자들은 모든 모델을 256$\times$256 크기의 저해상도 이미지에서 사전 학습시킨 다음, 혼합된 종횡비를 가진 더 높은 해상도에서 모델을 fine-tuning하였다. 고해상도로 이동하면 mixed precision 학습이 불안정해지고 loss가 발산할 수 있다. 이는 full precision 학습으로 전환하면 해결할 수 있지만 mixed precision 학습에 비해 성능이 약 2배 떨어진다.

ViT-22B 논문에서는 attention 엔트로피가 통제 불가능하게 증가하기 때문에 대형 ViT의 학습이 발산한다는 것을 관찰했으며, 이를 방지하기 위해 attention 연산 전에 query와 key를 정규화할 것을 제안하였다. 저자들은 이 접근 방식을 따르고 MMDiT 아키텍처의 두 스트림 모두에서 학습 가능한 RMSNorm을 모델에 사용한다.

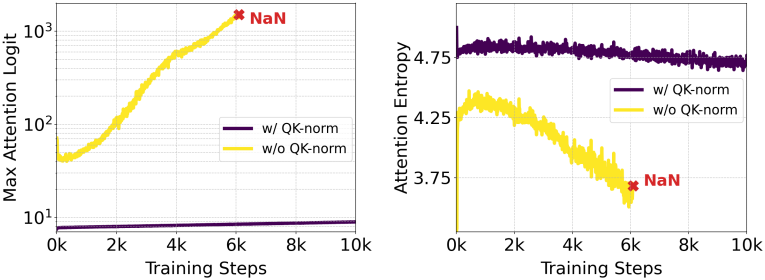
위 그림에서 볼 수 있듯이, 추가적인 정규화는 attention logit 성장의 불안정성을 방지하며, bf16 mixed precision에서 효율적인 학습을 가능하게 한다. 이 기술은 사전 학습 중에 정규화를 사용하지 않은 모델에도 적용할 수 있다. 모델은 추가 정규화 레이어에 빠르게 적응하고 보다 안정적으로 학습한다.

다양한 종횡비를 위한 위치 임베딩

저자들은 고정된 256$\times$256 해상도에서 학습한 후, 해상도를 높이고 유연한 종횡비로 inference를 가능하게 하는 것을 목표로 하였다. 2차원 위치 임베딩을 사용하므로 해상도에 따라 이를 조정해야 한다. 여러 종횡비 설정에서 임베딩을 직접 보간하면 측면 길이가 올바르게 반영되지 않는다. 대신 확장되고 보간된 위치 그리드를 조합하여 사용하고, 이후 주파수를 임베딩한다.

$S^2$개의 픽셀을 가진 타겟 해상도에 대해, bucketed sampling을 사용하여 각 batch가 균일한 크기 $H \times W \approx S^2$의 이미지로 구성되도록 한다. 최대 및 최소 학습 종횡비의 경우, 너비의 최대값 \(W_\textrm{max}\)와 높이의 최대값 \(H_\textrm{max}\)를 설정한다. Patching 후의 latent space에서의 크기에 따라 \(h_\textrm{max} = H_\textrm{max}/16\), \(w_\textrm{max} = W_\textrm{max}/16\), \(s = S/16\)로 둔다. 이 값들을 바탕으로 세로 위치 격자를 다음과 같이 구성한다.

\[\begin{equation} \left(\left( p - \frac{h_\textrm{max} - s}{2} \right) \cdot \frac{256}{S} \right)_{p=0}^{h_\textrm{max}-1} \end{equation}\]

그리고 가로 위치에 대해서도 동일한 방식으로 격자를 구성한다. 이후, 생성된 2D 위치 격자에서 중앙을 crop한 다음, 임베딩을 수행한다.

해상도에 따른 timestep schedule shifting

직관적으로, 해상도가 높을수록 픽셀이 더 많으므로 신호를 파괴하기 위해 더 많은 noise가 필요하다. $n = H \cdot W$개의 픽셀을 가진 해상도에서, 모든 픽셀의 값이 $c \in \mathbb{R}$인 상수 이미지를 고려하자.

\[\begin{equation} z_t = (1 − t) c \unicode{x1D7D9} + t \epsilon \end{equation}\]

$z_t$는 확률 변수 $Y = (1 − t)c + t\eta$에 대한 $n$개의 관측치를 제공한다. $\eta \sim \mathcal{N}(0,1)$이므로 $\mathbb{E}(Y) = (1 − t)c$이고 $\sigma(Y) = t$이다.

따라서 $c = \frac{1}{1-t} \mathbb{E}(Y)$를 통해 $c$를 복구할 수 있다. $Y$의 표준 오차는 $\frac{t}{\sqrt{n}}$이기 때문에, $c$와 샘플 추정치 $\hat{c} = \frac{1}{1-t} \sum_{i=1}^n z_{t,i}$ 간의 오차는 $\sigma(t, n) = \frac{t}{1-t} \sqrt{\frac{1}{n}}$의 표준 편차를 갖는다. 따라서 이미 이미지 $z_0$가 픽셀 전체에서 일정하다는 것을 알고 있다면 $\sigma(t, n)$은 $z_0$에 대한 불확실성의 정도를 나타낸다. 예를 들어, 너비와 높이를 두 배로 하면 불확실성이 절반으로 줄어든다.

이제 해상도 $n$의 timestep $t_n$을 해상도 $m$의 timestep $t_m$에 매핑하여, 즉 $\sigma (t_n, n) = \sigma (t_m, m)$을 풀어 동일한 불확실성 수준을 얻을 수 있다.

\[\begin{equation} t_m = \frac{\sqrt{\frac{m}{n}} t_n}{1 + (\sqrt{\frac{m}{n}} - 1) t_n} \end{equation}\]

다음은 timestep schedule shifting 결과이다.

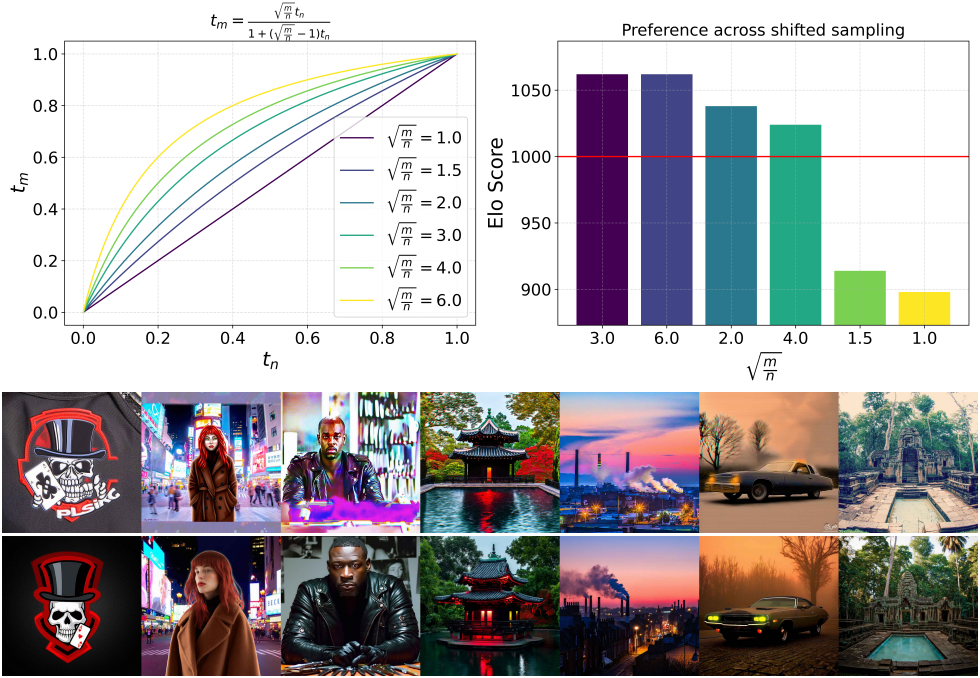
다음은 SOTA 이미지 생성 모델들과의 인간 선호도 평가 결과이다.

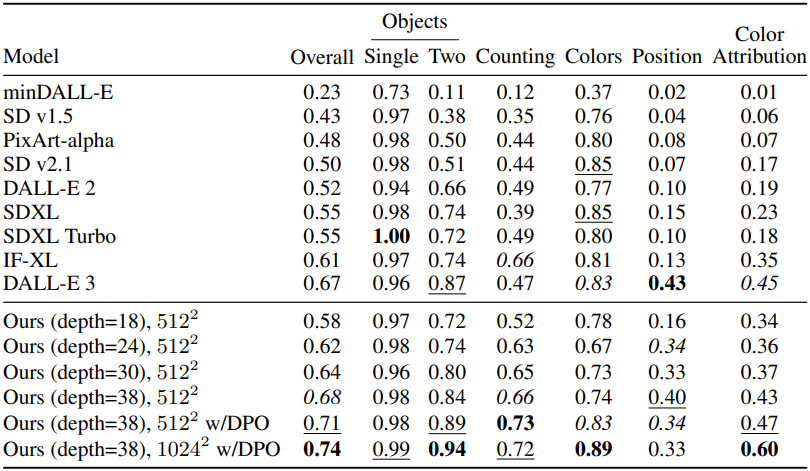
다음은 기존 방법들과의 GenEval 비교 결과이다.

다음은 모델 크기에 따른 샘플링 효율성을 비교한 표이다.

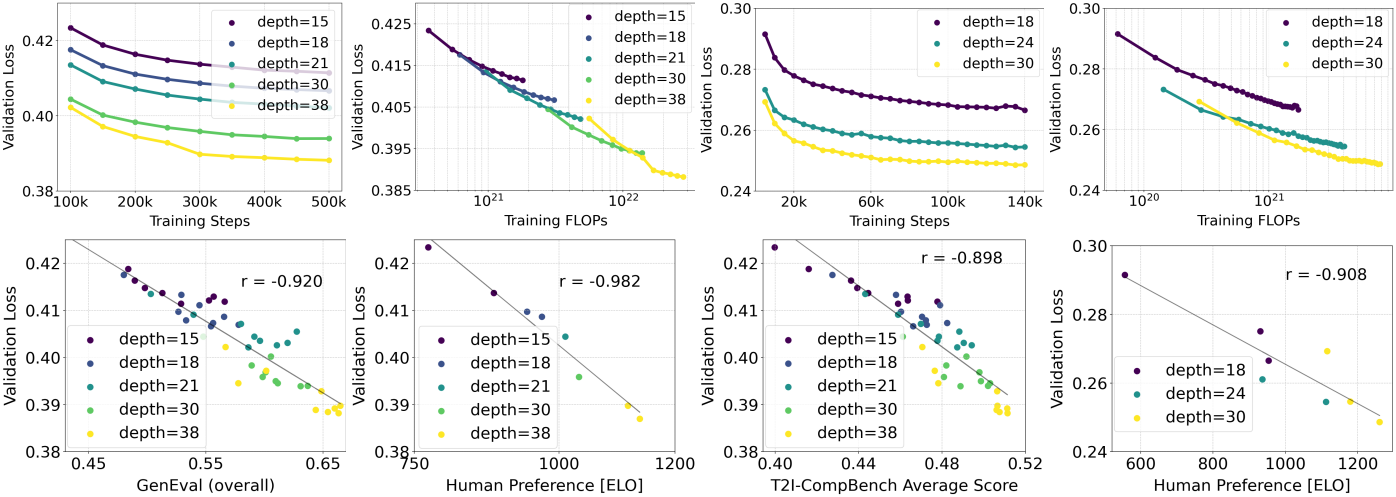
다음은 스케일링의 정량적 효과를 비교한 그래프들이다.

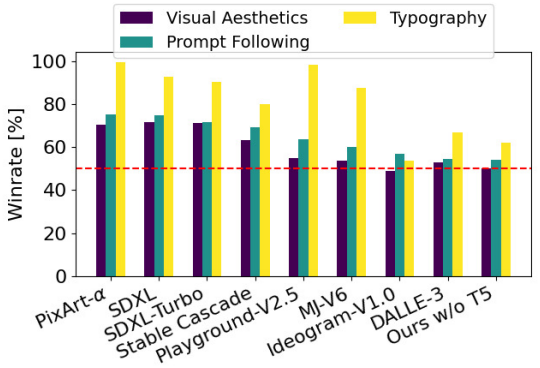
다음은 T5 유무에 따른 결과를 비교한 것이다. T5를 제거해도 미적 품질 평가에는 영향이 없고 (승률 50%), 프롬프트 준수에도 영향이 미미한 반면 (승률 46%), 텍스트 생성 능력에 대한 기여도는 더 크다 (승률 38%).