[논문리뷰] Star-Shaped Denoising Diffusion Probabilistic Models (SS-DDPM)

NeurIPS 2023. [Paper] [Github]
Andrey Okhotin, Dmitry Molchanov, Vladimir Arkhipkin, Grigory Bartosh, Aibek Alanov, Dmitry Vetrov
HSE University | Sber AI | AMLab | AIRI
10 Feb 2023

(DDPM과 SS-DDPM의 forward process 비교)

Introduction

Diffusion model의 주요 규칙은 forward process에서 정보를 파괴하고 이를 reverse process에서 복구하는 것이다. DDPM과 같은 기존 diffusion model에서는 Gaussian noise를 주입하여 정보를 파괴하며, 이미지와 같은 일부 데이터 타입에는 합리적이다. 하지만, 매니폴드나 닫힌 부피에 분포된 데이터나 다른 feature를 가지는 데이터에 Gaussian noise를 주입하는 것은 부자연스러울 수 있으며 데이터 구조를 파괴한다. 이런 데이터의 경우 데이터 구조를 유지하는 non-Gaussian noise를 사용해야 한다.

불행히도 기존 diffusion model의 noise 분포를 교체하는 방법은 분명하지 않다. 문제는 Markov noising process를 정의하는 분포와 주변 분포 사이의 연결을 유지해야 한다는 것이다. 다른 연구들에서 델타 함수나 감마 분포와 같은 다른 분포에 대하여 연구하였지만 각각의 경우에 대한 특별한 방법을 제공했을 뿐이다.

본 논문에서는 Gaussian DDPM을 noise 분포의 exponential family로 일반화하는 새로운 접근 방식인 Star-Shaped Denoising Diffusion Probabilistic Models (SS-DDPM)을 제안한다. SS-DDPM에서는 각 diffusion step에서 주변 분포를 정의한다. 저자들은 SS-DDPM의 유도 과정을 보이고, 효율적인 샘플링 및 학습 알고리즘을 디자인하고, DDPM과의 동등성을 보인다.

Theory

1. DDPMs

Gaussian DDPM은 forward process $q^\textrm{DDPM} (x_{0:T})$와 대응되는 reverse process $p_\theta^\textrm{DDPM} (x_{0:T})$로 정의된다. Forward process는 다음과 같은 Markov chain으로 정의된다.

\[\begin{equation} q^\textrm{DDPM} (x_{0:T}) = q(x_0) \prod_{t=1}^T q^\textrm{DDPM} (x_t \vert x_{t-1}) \\ q^\textrm{DDPM} (x_t \vert x_{t-1}) = \mathcal{N} (x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) \end{equation}\]

여기서 $q(x_0)$은 데이터 분포이다. 파라미터 $\beta_t$는 사전에 선택되고 고정되며, diffusion process의 noise schedule을 정의한다. Noise schedule은 $x_T$가 더 이상 $x_0$에 의존하지 않고 표준 가우시안 분포를 따르도록 선택된다.

\[\begin{equation} q^\textrm{DDPM} (x_T) = \mathcal{N} (x_T; 0, I) \end{equation}\]

Reverse process는 비슷한 구조를 따르며 모델의 생성 부분을 구성한다.

\[\begin{equation} p_\theta^\textrm{DDPM} (x_{0:T}) = q^\textrm{DDPM} (x_T) \prod_{t=1}^T p_\theta^\textrm{DDPM} (x_{t-1} \vert x_t) \\ p_\theta^\textrm{DDPM} (x_{t-1} \vert x_t) = \mathcal{N} (x_{t-1}; \mu_\theta (x_t, t), \Sigma_\theta (x_t, t)) \end{equation}\]

DDPM의 forward process는 일반적으로 고정되며 reverse process에 모든 파라미터가 포함된다. 이 파라미터들은 학습 데이터의 likelihood에 대한 variational lower bound (VLB)를 최대화하도록 학습된다.

\[\begin{aligned} \mathcal{L}^\textrm{DDPM} (\theta) &= \mathbb{E}_{q^\textrm{DDPM}} \bigg[ \log p_\theta^\textrm{DDPM} (x_0 \vert x_1) \\ &- \sum_{t=2}^T D_{KL} (q^\textrm{DDPM} (x_{t-1} \vert x_t, x_0) \| p_\theta^\textrm{DDPM} (x_{t-1} \vert x_t)) \bigg] \end{aligned}\]

2. Limitation of DDPMs

예를 들어 단위 구에 분산된 데이터에 대한 생성 모델을 구성하는 task를 맡았다고 가정하자. 기존의 DDPM을 활용하는 것을 고려하고 싶을 수도 있지만 이러한 모델은 데이터를 유클리드 공간의 점으로 취급하므로 noisy한 개체가 더 이상 단위 구에 있지 않는다. 결과적으로 생성 모델은 주어진 문제의 디테일에서 이미 알려진 것, 즉 실제 데이터가 단위 구에 분산되어 있다는 것을 배우기 위해 자원의 상당 부분을 소비할 것이다.

보다 효율적인 방법은 noisy한 개체가 같은 구에 남아 있도록 noise를 주입하는 것이다. 그러면 모델은 매니폴드를 학습하는 데 제한된 리소스를 낭비하지 않고 디자인상 그 위에 놓이는 객체를 생성한다. 이러한 noise를 생성하는 한 가지 가능한 방법은 von Mises–Fisher 분포를 사용하는 것이다. DDPM을 구성하기 위해서는 diffusion의 두 인접 step인 $x_{t-1}$과 $x_t$ 사이의 transition을 정의해야 한다. 예를 들어 von Mises–Fisher 분포 $q(x_t \vert x_{t-1})$에서 $x_{t−1}$의 모드와 큰 concentration parameter $\kappa$를 사용하여 샘플링할 수 있다.

그러나 주변 분포의 명시적 형식 $q(x_t \vert x_0)$도 필요하므로 문제가 발생한다. 이는 $q(x_{t-1} \vert x_t, x_0)$의 계산에 필요하다. 이러한 주변 분포 자체가 conjugate prior이기 때문에 가우시안 또는 감마 noise에 대해 계산될 수 있으며 불연속 데이터의 경우 카테고리형 분포에 대해 계산될 수 있다. 그러나 일반적으로 DDPM을 구성하는 데 중요한 요구 사항인 명시적 형식의 transition 분포와 주변 분포를 모두 알 수 없다. 이와 같이 기존의 DDPM 프레임워크는 현재 Gaussian, Gamma 또는 categorical 이외의 noise 주입을 처리할 수 없다. 이 한계를 극복하기 위해 transition 분포 $q(x_t \vert x_{t-1})$의 명시적 정의를 피하고 대신 주변 분포 $q(x_t \vert x_0)$에서 시작하여 diffusion model을 구축하는 방식을 변경해야 한다.

3. Star-Shaped DDPMs

앞서 언급했듯이 DDPM model을 다른 분포로 확장하는 것은 매우 어렵다. 특히, $q(x_t \vert x_{t-1})$를 정의해야 $q(x_t \vert x_0)$를 명시적 형식으로 계산할 수 있으며, 사후 확률 분포 $q(x_{t-1} \vert x_t, x_0)$도 계산해야 한다.

이러한 어려움에 비추어 본 논문은 정의와 손실 함수의 유도에서 $q(x_t \vert x_0)$에만 의존하는 모델을 구성할 것을 제안한다.

Non-Markovian forward process $q^\textrm{SS} (x_{0:T})$를 가지는 star-shaped diffusion을 다음과 같은 구조로 정의한다.

\[\begin{equation} q^\textrm{SS} (x_{0:T}) = q(x_0) \prod_{t=1}^T q^\textrm{SS} (x_t \vert x_0) \end{equation}\]

DDPM과 달리 모든 $x_t$는 Markov chain을 구성하는 대신 주어진 $x_0$에 조건부로 독립적이다. Forward process의 이러한 구조를 통해 다른 noise 분포를 활용할 수 있다.

4. Defining the reverse model

DDPM에서는 reverse model이 Markovian 구조이며, 효율적인 순차적 생성 알고리즘이 가능하다.

\[\begin{equation} q^\textrm{DDPM} (x_{0:T}) = q^\textrm{DDPM} (x_T) \prod_{t=1}^T q^\textrm{DDPM} (x_{t-1} \vert x_t) \end{equation}\]

Star-shaped diffusion의 경우 Markovian 가정이 깨진다.

\[\begin{equation} q^\textrm{SS} (x_{0:T}) = q^\textrm{SS} (x_T) \prod_{t=1}^T q^\textrm{SS} (x_{t-1} \vert x_{t:T}) \end{equation}\]

결과적으로 실제 reverse process를 $x_{t:T}$로 컨디셔닝된 모델로 근사하여야 한다.

\[\begin{equation} p_\theta^\textrm{SS} (x_{0:T}) = p_\theta^\textrm{SS} (x_T) \prod_{t=1}^T p_\theta^\textrm{SS} (x_{t-1} \vert x_{t:T}) \end{equation}\]

$x_t$만을 사용하는 대신 $x_{t:T}$를 사용하는 것이 star-shaped model에서 $x_{t-1}$을 예측하는 데 중요하다.

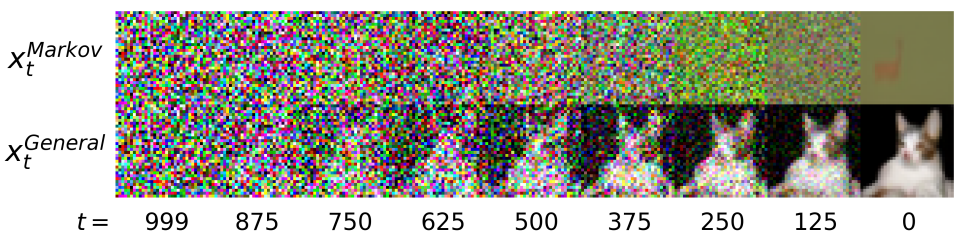
Markov model을 사용하여 실제 reverse process를 근사화하려고 시도하면 VLB에 줄일 수 없는 상당한 간격을 도입한다. 더 결정적으로, 이러한 샘플링 절차는 위 그림에서 볼 수 있는 것처럼 현실적인 샘플을 생성하지 못한다. 직관적으로 DDPM에서 $x_{t+1}$에 포함된 $x_0$에 대한 정보는 $x_t$에 포함된 $x_0$에 대한 정보에 중첩된다. 그래서 $x_t$를 알면 $x_{t+1}$을 버릴 수 있다. 그러나 star-shaped diffusion에서는 모든 변수가 $x_0$에 대한 독립적인 정보를 포함하므로 예측할 때 모두 고려해야 한다.

VLB는 다음과 같다.

\[\begin{aligned} \mathcal{L}^\textrm{SS} (\theta) &= \mathbb{E}_{q^\textrm{SS}} \bigg[ \log p_\theta (x_0 \vert x_{1:T}) \\ &- \sum_{t=2}^T D_{KL} (q^\textrm{SS} (x_{t-1} \vert x_0) \| p_\theta^\textrm{SS} (x_{t-1} \vert x_{t:T})) \bigg] \end{aligned}\]

이 VLB를 사용하면 모델을 정의하고 학습하는 데 $q{x_{t-1} \vert x_0}$만 필요하며, 넓은 범위의 noising 분포를 사용할 수 있게 된다. 예측 모델 $p_\theta (x_{t-1} \vert x_{t:T})$를 전체 $x_{t:T}$로 컨디셔닝하는 것이 실용적이지 못하기 때문에 저자들은 reverse process를 구현하는 보다 효율적인 방법을 제안한다.

5. Efficient tail conditioning

전체 $x_{t:T}$를 사용하는 대신 변수 \(G_t = \mathcal{G}_t (x_{t:T})\)를 정의하여 $x_0$에서 $x_{t:T}$까지의 전체 정보를 추출한다. 즉, 다음과 같은 등식이 유지되기를 바란다.

\[\begin{equation} q^\textrm{SS} (x_{t-1} \vert x_{t:T}) = q^\textrm{SS} (x_{t-1} \vert G_t) \end{equation}\]

$G_t$를 정의하는 방법 중 하나는 모든 변수 $x_{t:T}$를 하나의 벡터로 concat하는 것이다. 하지만, 이는 차원이 계속 증가하므로 실용적이지 않다.

$G_t$는 $x_{t:T}$에 대한 sufficient statistics의 역할을 한다. Pitman–Koopman–Darmois (PKD) 정리에 따르면 상수 차원을 가진 sufficient statistics는 exponential family만으로 표현할 수 있다고 한다.

PKD에 영감을 받아 본 논문은 분포들의 exponential family를 사용한다. Star-shaped diffusion의 경우 샘플들이 독립적으로 분포되지 않으므로 PKD를 바로 적용할 수 없다. 하지만 sufficient tail statistic $G_t$를 exponential family의 특정 부분집합으로 정의할 수 있으며, 이를 exponential family with linear parameterization이라고 부른다.

---

Theorem 1.

\[\begin{equation} q^\textrm{SS} (x_t \vert x_0) = h_t (x_t) \exp \{ \eta_t (x_0)^\top \mathcal{T} (x_t) - \Omega_t (x_0) \} \\ \eta_t (x_0) = A_t f (x_0) + b_t \\ G_t = \mathcal{G}_t (x_{t:T}) = \sum_{s=t}^T A_s^\top \mathcal{T} (x_s) \end{equation}\]

이 주어지면 다음이 성립한다.

\[\begin{equation} q^\textrm{SS} (x_{t-1} \vert x_{t:T}) = q^\textrm{SS} (x_{t-1} \vert G_t) \end{equation}\]

---

대부분의 경우 Theorem 1의 전제는 관련된 분포의 family(군)보다는 분포의 parameterization를 제한한다. Exponential family의 광범위한 분포에 대한 선형 parameterization를 쉽게 생각해낼 수 있다. 예를 들어 베타 분포 $q(x_t \vert x_0) = \textrm{Beta} (x_t; \alpha_t, \beta_t)$에 대해 $x_0$를 분포의 모드로 사용하고 새로운 concentration parameter $\nu_t$를 도입하여 선형 parameterization을 얻을 수 있다.

\[\begin{equation} \alpha_t = 1 + \nu_t x_0 \\ \beta_t = 1 + \nu_t (1 - x_0) \end{equation}\]

PKD와 마찬가지로 이 트릭은 exponential family의 부분집합에만 가능하다. 일반적으로 $G_t$의 차원은 $x_{t:T}$의 크기에 따라 증가한다. 이 경우에도 여전히 SS-DDPM을 적용할 수 있지만, $G_t$를 구성하는 것은 더 조심스러운 고려가 필요하다.

6. Final model definition

VLB를 최대화하기 위해 reverse process의 각 step은 실제 reverse 분포를 근사해야 한다.

\[\begin{aligned} p_\theta^\textrm{SS} (x_{t-1} \vert x_{t:T}) & \approx q^\textrm{SS} (x_{t-1} \vert x_{t:T}) \\ & = \int q^\textrm{SS} (x_{t-1} \vert x_0) q^\textrm{SS} (x_0 \vert x_{t:T}) dx_0 \end{aligned}\]

DDPM과 비슷하게, 모델 \(x_\theta (\mathcal{G}_t (x_{t:T}), t)\)의 예측을 중심으로 델타 함수를 사용하여 $q^\textrm{SS} (x_0 \vert x_{t:T})$를 근사하도록 선택한다. 그 결과 SS-DDPM의 reverse process에 대한 다음과 같은 정의를 할 수 있다.

\[\begin{equation} p_\theta^\textrm{SS} (x_{t-1} \vert x_{t:T}) = q^\textrm{SS} (x_{t-1} \vert x_0) |_{x_0 = x_\theta (\mathcal{G})_t (x_{t:T}, t)} \end{equation}\]

DDPM과 같이 분포 $p_\theta^\textrm{SS} (x_0 \vert x_{1:T})$는 분산이 작은 분포 $p^\textrm{SS} (x_0 \vert x_1)$으로 고정될 수 있다.

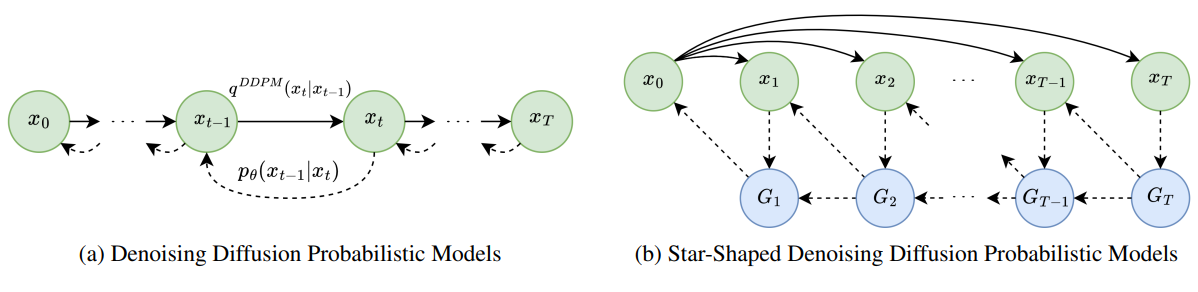
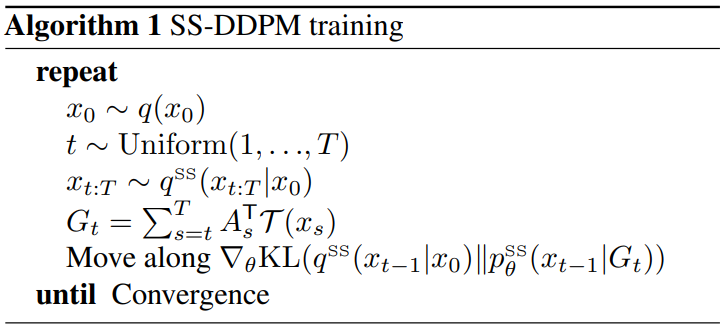
앞서 설명한 forward process와 VLB 목적 함수로 SS-DDPM model의 일반적인 정의가 가능하다. 모델 구조는 위 그림과 같다. 학습 및 샘플링 알고리즘은 Algorithm 1과 2와 같다.

   

결과 모델은 DDPM과 유사하다. 낮은 분산의 분포 ($t = 1$)에서 시작하여 $x_0$와 $x_t$ 사이의 공유된 정보가 없을 때($t = T$)까지 점진적으로 $q^\textrm{SS} (x_t \vert x_0)$의 엔트로피를 증가시킨다.

7. Connection to DDPMs

$G_t$는 $x_t$의 star-shaped process에 대해 dual process로 볼 수 있는 diffusion과 유사한 Markov process를 형성한다. 놀랍게도, Gaussian SS-DDPM에서 이 dual process는 Gaussian DDPM 그 자체이다.

---

Theorem 2.

$\bar{\alpha}_t^\textrm{DDPM}$이 DDPM model의 noising schedule을

\[\begin{equation} \beta_t = \frac{\bar{\alpha}_{t-1}^\textrm{DDPM} - \bar{\alpha}_t^\textrm{DDPM}}{\bar{\alpha}_{t-1}^\textrm{DDPM}} \end{equation}\]

로 정의한다고 하자. 그리고 $q^\textrm{SS}(x_{0:T})$가 다음과 같은 noising schedule과 tail statistics를 가진 Gaussian SS-DDPM forward process라고 하자.

\[\begin{equation} q^\textrm{SS} (x_t \vert x_0) = \mathcal{N} (x_t; \sqrt{\vphantom{1} \bar{\alpha}_t^\textrm{SS}} x_0, 1 - \bar{\alpha}_t^\textrm{SS}) \\ \mathcal{G}_t (x_{t:T}) = \frac{1 - \bar{\alpha}_t^\textrm{DDPM}}{\sqrt{\vphantom{1} \bar{\alpha}_t^\textrm{DDPM}}} \sum_{s=t}^T \frac{\sqrt{\vphantom{1} \bar{\alpha}_s^\textrm{DDPM}} x_s}{1 - \bar{\alpha}_s^\textrm{SS}} \\ \frac{\bar{\alpha}_t^\textrm{SS}}{1 - \bar{\alpha}_t^\textrm{SS}} = \frac{\bar{\alpha}_t^\textrm{DDPM}}{1 - \bar{\alpha}_t^\textrm{DDPM}} - \frac{\bar{\alpha}_{t+1}^\textrm{DDPM}}{1 - \bar{\alpha}_{t+1}^\textrm{DDPM}} \end{equation}\]

그러면 $G_t$는 $\bar{\alpha}_t^\textrm{DDPM}$에 의해 정의되는 Gaussian DDPM noising process

\[\begin{equation} q^\textrm{DDPM}(x_{0:T})|_{x_{1:T} = G_{1:T}} \end{equation}\]

를 따르며, 대응되는 reverse process와 VLB 목적 함수도 Gaussian DDPM과 같다.

---

Gaussian SS-DDPM이 Gaussian DDPM과 같기 때문에 SS-DDPM은 DDPM model을 직접 일반화한다고 볼 수 있다. 일반적인 경우, $G_t$를 위한 Markov diffusion process의 명시적 설명에 문제가 있으며 $x_t$를 위한 star-shaped model을 직접 사용하는 것이 더 쉽다.

Practical considerations

모델이 적절하게 정의되었다면 star-shaped diffusion의 효율성을 위한 몇가지 실용적인 고려가 필요하다.

Choosing the right schedule

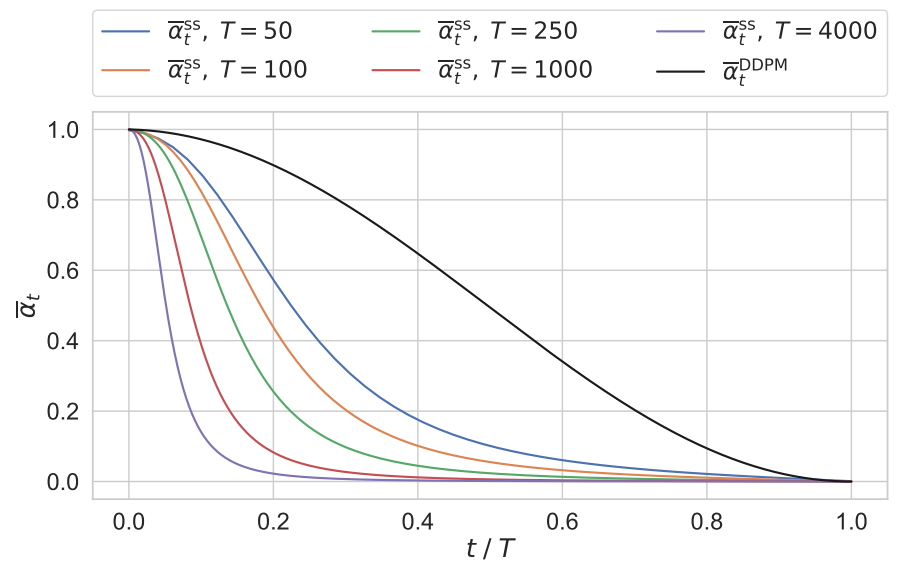
SS-DDPM model을 위한 알맞은 noising schedule을 선택하는 것이 중요하다. 이는 diffusion step $T$의 수에 따라 크게 달라지며 다양한 noising schedule이 주어지면 다르게 동작한다. 이는 동일한 cosine schedule을 가진 DDPM과 동등한 Gaussian SS-DDPM에 대한 noising schedule을 보여주는 위 그림에 설명되어 있다.

변수 $G_t$는 DDPM과 유사한 프로세스를 따르기 때문에 이미 잘 작동하는 것으로 알려진 DDPM noising schedule을 어떻게든 재사용하는 것이 좋다. 가우시안 분포의 경우 수치적으로

\[\begin{equation} I(x_0; G_t) = I(x_0; x_t^\textrm{DDPM}) \end{equation}\]

을 동일시하여 DDPM noising schedule을 해당 SS-DDPM noising schedule으로 변환할 수 있다. 일반적으로 모든 timestep $t$에 대해 DDPM 모델에 대한 상호 정보 $I(x_0; x_t^\textrm{DDPM})$와 거의 동일한 레벨의 상호 정보 $I(x_0; G_t) $를 갖는 schedule을 찾는다. 저자들은 Kraskov 및 DSIVI estimator를 사용하여 상호 정보를 추정하고 noising schedule과 일치하도록 look-up table을 구축한다. Beta SS-DDPM에 대한 schedule을 다음 그림에 설명되어 있다.

Implementing the sampler

샘플링 중에 Algorithm 2에 설명된 대로 overhead 없이 $G_t$를 증가시킬 수 있다. 그러나 학습 중에는 손실 함수를 추정하기 위해 각 개체에 대한 tail statistics를 샘플링해야 한다. 이를 위해 forward process $q^\textrm{SS}(x_{t:T} \vert x_0)$에서 $x_{t:T}$를 샘플링한 다음 $G_t$를 계산해야 한다. 실제로 이것은 눈에 띄는 overhead를 추가하지 않으며 필요한 경우 학습 프로세스와 병렬로 계산할 수 있다.

Reducing the number of steps

DDPM에서는 일부 timestamp를 건너뛰면 더 효율적으로 샘플링할 수 있다. 이는 Step 수를 변경하면 noising schedule을 변경해야 하고 결과적으로 모델을 재학습해야 하기 때문에 SS-DDPM에는 작동하지 않는다.

그러나 여전히 유사한 트릭을 사용하여 함수 평가 횟수를 줄일 수 있다. 일부 timestamp $x_{t_1+1:t_2−1}$을 건너뛰는 대신 현재 예측 $x_\theta(G_{t_2}, t_2)$를 사용하여 forward process에서 추출한 다음 이 샘플을 사용하여 $G_{t_1}$을 얻을 수 있다. Gaussian SS-DDPM의 경우 이는 해당 DDPM에서 이러한 timestamp를 건너뛰는 것과 같다. 일반적으로 다른 reverse process를 사용하여 reverse process를 근사한다.

\[\begin{aligned} p_\theta^\textrm{SS} (x_{t_1 : t_2} \vert G_{t_2}) &= \prod_{t = t_1}^{t_2} q^\textrm{SS} (x_t \vert x_0) |_{x_0 = x_\theta (G_t, t)} \\ & \approx \prod_{t = t_1}^{t_2} q^\textrm{SS} (x_t \vert x_0) |_{x_0 = x_\theta (G_{t_2}, t_2)} \end{aligned}\]

실제로 저자들은 SS-DDPM과 DDPM에 대한 함수 평가 횟수에 대한 유사한 의존성을 관찰했다고 한다.

Time-dependent tail normalization

Theorem 1에서 정의된 것처럼, tail statistics는 서로 다른 timestamp에서 매우 다른 스케일을 가질 수 있다. Tail statistics를 신경망에서 사용하기에 적합하게 만들려면 적절한 정규화가 중요하다.

Tail statistics를 계수의 합으로 정규화하는 것은 충분하지 않다. 대신에, 학습 데이터셋에서 tail statistics의 시간에 의존하는 평균과 분산을 모은 다음 표준 정규 분포로 정규화할 수 있다.

적절한 정규화는 tail statistics의 시각화에도 중요하다. Tail statistic의 평균과 분산을 학습 데이터 $\mathcal{T}(x_0)$의 sufficient statistics와 일치시킨 후 정규화된 $G_t$를 $\tilde{G}_t$를 $\mathcal{T}^{-1} (\tilde{G}_t)$를 사용하여 데이터 도메인에 매핑할 수 있으며, 데이터 도메인에서 시각화하면 된다.

Architectural choices

모델의 학습을 쉽게 만들기 위해 신경망과 손실 함수에 몇가지 수정이 필요하다.

신경망 $x_\theta (G_t, t)$는 $G_t$를 입력으로 받아 $x_0$의 추정치를 출력으로 생성한다. SS-DDPM에서 데이터 $x_0$를 어떤 매니폴드에 있을 수 있다. 따라서 신경망의 출력을 해당 매니폴드에 매핑해야 한다. 저자들은 이를 각 케이스별로 진행하였다.

VLB의 서로 다른 항은 굉장히 스케일이 다를 수 있다. 이런 이유로 DDPM에서는 VLB 대신 $L_\textrm{simple}$을 손실 함수로 사용한다. SS-DDPM도 비슷한 관점에서 재가중된 VLB를 사용한다.

Experiments

1. Geodesic data

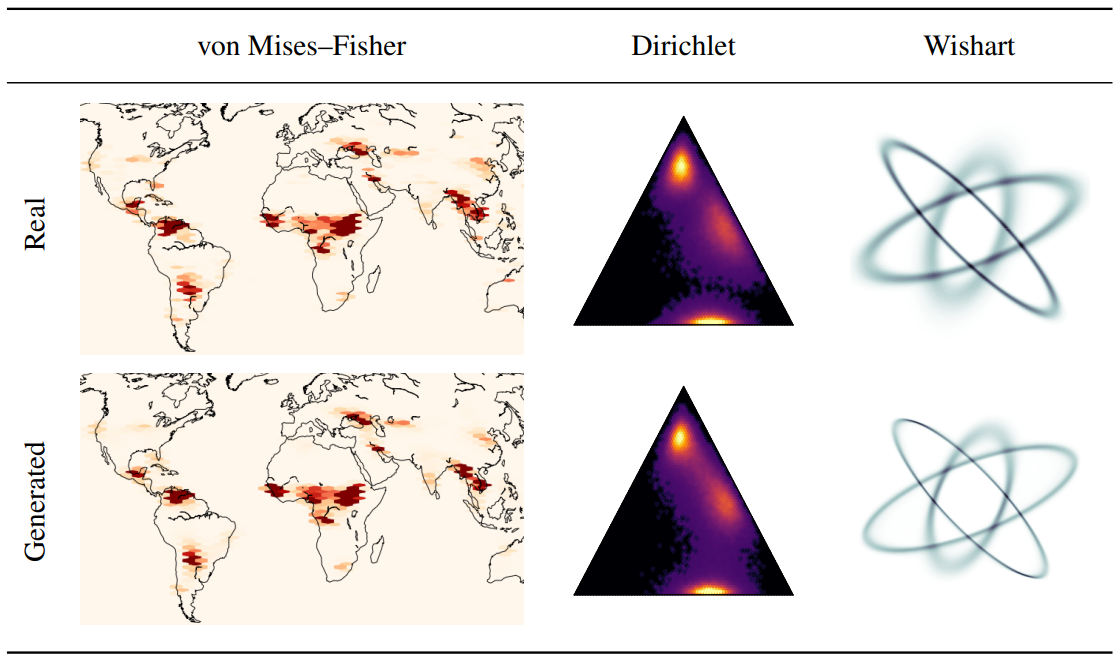
저자들은 3차원 von Mises-Fisher 분포를 사용하여 지표면 화재의 측지선 데이터셋인 EOSDIS에 SS-DDPM을 적용하였다. 손실 함수는 다음과 같다.

\[\begin{equation} \sum_{t=1}^T (1 - x_0^\top x_\theta (G_t, t)) \end{equation}\]

예측값을 단위 구에 매핑하기 위해 MLP의 3차원 출력을 정규화한다.

실험 결과는 위의 표에서 확인할 수 있다.

2. Synthetic data

저자들은 3차원 확률 simplex에서 객체를 생성하는 합성 문제에 대해 Dirichlet SS-DDPM을 평가하였다. 학습 데이터로 파라미터가 다른 3개의 Dirichlet 분포를 혼합하여 사용하였다. 예측을 도메인에 매핑하기 위해 MLP 위에 Softmax 함수를 배치했으며, VLB를 수정 없이 최적화하였다.

저자들은 $2 \times 2$ 크기의 positive definite matrix를 생성하는 합성 문제에서 Wishart SS-DDPM을 평가하였다. 서로 다른 파라미터가 있는 3개의 Wishart 분포를 혼합하여 학습 데이터로 사용하였다. Symmetric positive definite matrices $V$의 경우 MLP는 Cholesky 분해 $V_\theta = L_\theta L_\theta^\top$에서 lower triangular factor $L_\theta$를 예측한다. Wishart 분포에서 샘플링의 안정성과 손실 함수 추정을 위해 예측된 $V_\theta$에 스칼라 행렬 $10^{−4} I$를 추가한다. Wishart SS-DDPM에서는 $L_{simple}$의 아날로그를 손실 함수로 사용한다. 학습 안정성을 개선하기 위해 timestamp $t$에 해당하는 각 KL 항을 사용된 noising schedule의 사실상 concentration parameter인 $n_t$로 나눈다. Dirichlet 케이스와 유사한 MLP를 학습하고 학습 불안정성을 완화하기 위해 exponential learning rate scheduler를 추가로 사용한다.

두 경우의 실험 결과는 모두 위의 표에서 확인할 수 있다.

3. Images

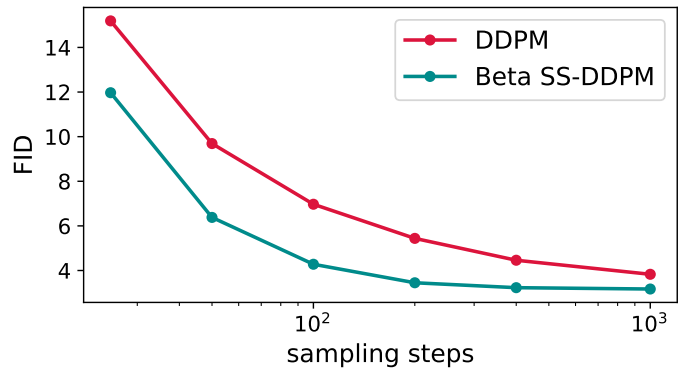
마지막으로 저자들은 CIFAR-10에서 Beta SS-DDPM을 평가하였다. 학습 데이터가 일반적으로 $[0, 1]$로 제약되기 때문에 Beta diffusion을 이미지에 적용할 수 있다. NCSN++의 신경망과 학습 전략을 사용했다. NCSN++ 위에 sigmoid 함수를 추가하여 예측값을 데이터 도메인으로 매핑하였다.

실험 결과는 아래 그래프와 같다.