[논문리뷰] Image Super-Resolution via Iterative Refinement (SR3)
arXiv 2021. [Paper]
Chitwan Saharia, Jonathan Ho, William Chan, Tim Salimans, David J. Fleet, Mohammad Norouzi
Google Research, Brain Team
30 Jun 2021

Introduction
Super-resolution은 입력된 저해상도 이미지와 일치하는 고해상도 이미지를 생성하는 프로세스이다. Colorization, inpainting, de-blurring과 함께 광범위한 image-to-image translation task에 속한다. 이러한 많은 inverse problem과 마찬가지로 super-resolution은 여러 출력 이미지가 하나의 입력 이미지와 일치할 수 있고, 주어진 입력에 대한 출력 이미지의 조건부 분포가 일반적으로 간단한 parametric 분포이다. 따라서 feedforward convolutional network를 사용하는 단순 회귀 기반 방법은 낮은 배율에서 super-resolution에 사용할 수 있지만 높은 배율에는 디테일이 부족한 경우가 많다.
심층 생성 모델은 이미지의 복잡한 경험적 분포를 학습하는 데 성공했다. Autoregressive model, VAE, Normalizing Flow (NF), GAN은 설득력 있는 이미지 생성 결과를 보여주었고 super-resolution과 같은 조건부 task에 적용되었다. 그러나 이러한 접근 방식에는 종종 다양한 제한 사항이 있다. 예를 들어, autoregressive model은 고해상도 이미지 생성에 엄청나게 비싸고, NF와 VAE는 종종 좋지 못한 샘플 품질을 보이며, GAN은 최적화 불안정성과 mode collapse를 피하기 위해 신중하게 설계된 정규화 및 최적화 트릭이 필요하다.
본 논문은 조건부 이미지 생성에 대한 새로운 접근 방식인 Super-Resolution via Repeated Refinement (SR3)를 제안한다. 이는 DDPM과 denoising socre matching에서 영감을 얻었다. SR3는 Langevin 역학과 유사한 일련의 refinement step을 통해 표준 정규 분포를 경험적 데이터 분포로 변환하는 방법을 학습하여 작동한다. 핵심은 출력에서 다양한 레벨의 noise를 반복적으로 제거하기 위해 denoising 목적 함수로 학습된 U-Net 아키텍처이다. U-Net 아키텍처에 대한 간단하고 효과적인 수정을 제안하여 DDPM을 조건부 이미지 생성에 적용한다. GAN과 달리 잘 정의된 loss function을 최소화한다. Autoregressive model과 달리 SR3는 출력 해상도에 관계없이 일정한 수의 inference step을 사용한다.
SR3는 다양한 배율과 입력 해상도에서 잘 작동한다. SR3 모델은 예를 들어 64$\times$64에서 256$\times$256으로, 그 다음에는 1024$\times$1024로 cascade할 수도 있다. Cascading model을 사용하면 배율이 높은 단일 대형 모델이 아닌 몇 개의 작은 모델을 독립적으로 학습시킬 수 있다. 고해상도 이미지를 직접 생성하려면 동일한 품질에 대해 더 많은 refinement step이 필요하기 때문에 cascading model이 보다 효율적인 inference를 가능하게 한다. 또한 저자들은 조건부 생성 모델을 SR3 모델과 연결하여 unconditional한 고충실도 이미지를 생성할 수 있음을 발견했다. 특정 도메인에 초점을 맞춘 기존 연구들과 달리 SR3는 얼굴과 자연스러운 이미지 모두에 효과적임을 보여준다.
PSNR과 SSIM과 같은 자동화된 이미지 품질 점수는 입력 해상도가 낮고 배율이 큰 경우 인간의 선호도를 잘 반영하지 못한다. 합성 디테일이 레퍼런스 디테일과 완벽하게 일치하지 않기 때문에 이러한 품질 점수는 종종 머리카락 질감과 같은 합성 고주파 디테일에 불이익을 준다. 저자들은 SR3의 품질을 비교하기 위해 사람의 평가에 의지한다. 인간 피험자에게 저해상도 입력을 보여주고 모델 출력과 ground-truth 이미지 중에서 선택해야 하는 2-alternative forced-choice(2AFC)를 채택한다. 이를 기반으로 이미지 품질과 저해상도 입력으로 모델 출력의 일관성을 모두 캡처하는 fool rate 점수를 계산한다. SR3는 SOTA GAN 방법과 강력한 회귀 baseline보다 훨씬 더 높은 fool rate를 달성하였다.
Conditional Denoising Diffusion Model
모르는 조건부 분포 $p(y \vert x)$에서 추출한 샘플을 나타내는 \(D = \{x_i , y_i\}_{i=1}^N\)로 표시된 입력-출력 이미지 쌍의 데이터셋이 제공된다. 이는 많은 타겟 이미지가 하나의 소스 이미지와 일치할 수 있는 일대다 매핑이다. 소스 이미지 $x$를 타겟 이미지 $y \in \mathbb{R}^d$에 매핑하는 확률적 반복 정제 프로세스를 통해 $p(y \vert x)$에 대한 parametric 근사를 학습하는 데 관심이 있다. 저자들은 조건부 이미지 생성에 대한 DDPM 모델을 적용하여 이 문제에 접근한다.
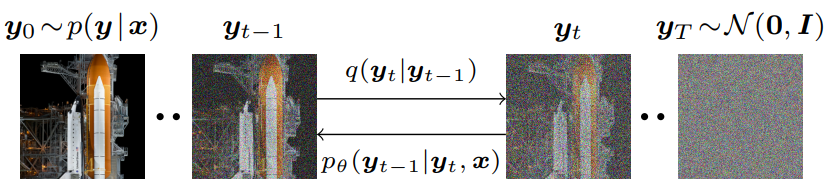
조건부 DDPM 모델은 $T$개의 refinement step에서 타겟 이미지 $y_0$을 생성한다. 모델은 순수한 noise 이미지 $y_T \sim \mathcal{N} (0, I)$에서 시작하여 $y_0 \sim p(y \vert x)$를 만족하는 학습된 조건부 transition 분포 $p_\theta (y_{t-1})$에 따라 $(y_{T -1}, y_{T -2}, \cdots, y_0)$을 통해 이미지를 반복적으로 정제한다 (위 그림 참고).
Inference chain에서 중간 이미지의 분포는 $q(y_t \vert y_{t−1})$로 표시되는 고정 Markov chain을 통해 신호에 Gaussian noise를 점진적으로 추가하는 forward diffusion process로 정의된다. 모델의 목적 함수는 $x$로 컨디셔닝된 reverse Markov chain을 통해 noise에서 신호를 반복적으로 복구하여 Gaussian diffusion process를 reverse시키는 것이다. 원본 이미지와 noisy한 타겟 이미지를 입력으로 사용하고 noise를 추정하는 denoising model $f_\theta$를 사용하여 reverse chain을 학습한다.
1. Gaussian Diffusion Process
먼저 $T$번의 iteration에 걸쳐 고해상도 이미지 $y_0$에 점진적으로 Gaussian noise를 추가하는 forward Markovian diffusion process $q$를 정의한다.
\[\begin{equation} q(y_{1:T} \vert y_0) = \prod_{t=1}^T q (y_t \vert y_{t-1}) \\ q(y_t \vert y_{t-1}) = \mathcal{N}(y_t \vert \sqrt{\alpha_t} y_{t-1}, (1-\alpha_t) I) \end{equation}\]여기서 스칼라 매개변수 $\alpha_{1:T}$는 $0 < \alpha_t < 1$인 hyper-parameter이며 각 iteration에서 추가되는 noise의 분산을 결정한다. $y_{t-1}$은 $\sqrt{\alpha_t}$만큼 감쇠되어 random variable의 분산이 $t \rightarrow \infty$로 제한된다. 예를 들어 $y_{t−1}$의 분산이 1이면 $y_t$의 분산도 1이다.
중요한 것은 중간 step을 다음과 같이 주어진 $y_0$에 대하여 $y_t$의 분포를 특성화할 수 있다는 것이다.
\[\begin{equation} q (y_t \vert y_0) = \mathcal{N} (y_t \vert \sqrt{\gamma_t} y_0 , (1-\gamma_t)I) \\ \gamma_t = \prod_{i=1}^t \alpha_i \end{equation}\]추가로 대수적 조작을 가하여 제곱을 완성하면 주어진 $(y_0, y_t)$에 대한 $y_{t-1}$의 사후 확률 분포를 다음과 같이 유도할 수 있다.
\[\begin{equation} q (y_{t-1} \vert y_0, y_t) = \mathcal{N} (y_{t-1} \vert \mu, \sigma^2 I) \\ \mu = \frac{\sqrt{\gamma_{t-1}} (1 - \alpha_t)}{1 - \gamma_t} y_0 + \frac{\sqrt{\alpha_t} (1 - \gamma_{t-1})}{1 - \gamma_t} y_t \\ \sigma^2 = \frac{(1 - \gamma_{t-1})(1-\alpha_t)}{1 - \gamma_t} \end{equation}\]2. Optimizing the Denoising Model
Diffusion process를 reverse하기 위해 소스 이미지 $x$의 형태로 추가 정보를 활용하고 이 소스 이미지 $x$와 noisy한 타겟 이미지 $\tilde{y}$를 입력으로 사용하는 denoising model $f_\theta$를 최적화한다.
\[\begin{equation} \tilde{y} = \sqrt{\gamma} y_0 + \sqrt{1 - \gamma} \epsilon, \quad \epsilon \sim \mathcal{N}(0, I) \end{equation}\]원본 이미지 $x$와 noisy한 타겟 이미지 $\tilde{y}$ 외에도 $f_\theta (x, \tilde{y} \gamma)$는 $\gamma$에 대한 충분한 통계를 입력으로 사용하고 noise 벡터 $\epsilon$을 예측하도록 학습된다. $f_\theta$가 스칼라 $\gamma$에 대한 컨디셔닝을 통해 noise level을 인식하도록 한다. $f_\theta$의 학습을 위해 제안된 목적 함수는 다음과 같다.
\[\begin{equation} \mathbb{E}_{(x, y)} \mathbb{E}_{\epsilon, \gamma} \bigg\| f_\theta (x, \tilde{y}, \gamma) - \epsilon \bigg\|_p^p \end{equation}\]$f_\theta$의 출력을 $\epsilon$로 회귀하는 대신 $f_\theta$의 출력을 $y_0$로 회귀할 수도 있다. $\gamma$와 $\tilde{y}$가 주어졌을 때 $\epsilon$과 $y_0$의 값은 결정론적으로 서로 도출될 수 있지만 회귀 타겟을 변경하면 loss function의 스케일에 영향을 미친다.
3. Inference via Iterative Refinement
Inference는 Gaussian noise $y_T$에서 시작하여 forward diffusion process의 반대 방향으로 진행되는 reverse Markovian process로 정의된다.
\[\begin{aligned} p_\theta (y_{0:T} \vert x) &= p(y_T) \prod_{t=1}^T p_\theta (y_{t-1} \vert y_t, x) \\ p(y_T) &= \mathcal{N} (y_T \vert 0, I) \\ p_\theta (y_{t-1} \vert y_t, x) &= \mathcal{N}(y_{t-1} \vert \mu_\theta (x, y_t, \gamma_t), \sigma_t^2 I) \end{aligned}\]학습된 $p_\theta (y_{t−1} \vert y_t, x)$로 inference process를 정의한다. Forward process step의 noise 분산이 가능한 한 작게 설정되면 최적의 reverse process $p(y_{t−1} \vert y_t, x)$는 대략 가우시안이 된다. 따라서 inference process에서 Gaussian conditionals를 선택하면 실제 reverse process에 합당한 적합성을 제공할 수 있다. 한편, $1−\gamma_T$는 $y_T$가 prior $p(y_T) = \mathcal{N}(y_T \vert 0, I)$에 따라 대략적으로 분포되도록 충분히 커야 샘플링 프로세스가 순수한 Gaussian noise에서 시작할 수 있다.
$f_\theta$가 주어진 $\tilde{y}$에 대하여 $\epsilon$을 추정하도록 학습되기 때문에 주어진 $y_t$에 대하여 다음과 같이 $y_0$를 근사할 수 있다.
\[\begin{equation} \hat{y}_0 = \frac{1}{\sqrt{\gamma_t}} (y_t - \sqrt{1 - \gamma_t} f_\theta (x, y_t, \gamma_t)) \end{equation}\]\(\hat{y}_0\)를 $q(y_{t-1} \vert y_0, y_t)$에 대입하여 $p_\theta (y_{t-1} \vert y_t, x)$의 평균을 parameterize할 수 있다.
\[\begin{equation} \mu_\theta (x, y_t, \gamma_t) = \frac{1}{\sqrt{\alpha_t}} \bigg( y_t - \frac{1 - \alpha_t}{\sqrt{1 - \gamma_t}} f_\theta (x, y_t, \gamma_t) \bigg) \end{equation}\]$p_\theta (y_{t-1} \vert y_t, x)$의 분산을 $(1-\alpha_t)$으로 설정한다.
이 parameterization에 따라 모델에서 각 iteration은 다음과 같은 형식을 취한다.
\[\begin{equation} y_{t-1} \leftarrow \frac{1}{\sqrt{\alpha_t}} \bigg( y_t - \frac{1 - \alpha_t}{\sqrt{1 - \gamma_t}} f_\theta (x, y_t, \gamma_t) \bigg) + \sqrt{1 - \alpha_t} \epsilon_t \end{equation}\]이는 데이터 로그 밀도의 기울기 추정치를 제공하는 $f_\theta$를 사용하는 Langevin 역학의 한 step과 유사하다.
4. SR3 Model Architecture and Noise Schedule
SR3 아키텍처는 DDPM에 있는 U-Net과 유사하며 수정된 사항이 있다. 원래 DDPM의 residual block을 BigGAN의 residual block으로 교체하고 skip connection을 $\sqrt{1/2}$ 로 re-scale한다. 또한 residual block의 수와 다른 해상도에서 채널 multiplier를 늘린다. 입력 $x$로 모델을 컨디셔닝하기 위해 bicubic interpolation을 사용하여 저해상도 이미지를 타겟 해상도로 upsampling한다. 결과는 채널 차원을 따라 $y_t$와 concat된다. 저자들은 FiLM 사용과 같은 보다 정교한 컨디셔닝 방법을 실험했지만 간단한 concatenation이 유사한 생성 품질을 생성한다는 것을 발견했다.
학습 noise schedule의 경우
\[\begin{equation} p(\gamma) = \sum_{t=1}^T \frac{1}{T} U(\gamma_{t-1}, \gamma_t) \end{equation}\]을 사용한다. 구체적으로 학습 중에 먼저 timestep \(t \sim \{0, \cdots, T\}\)를 균등하게 샘플링하고 $\gamma \sim U(\gamma_{t-1}, \gamma_t)$를 샘플링한다. 모든 실험에서 $T = 2000$으로 설정한다.
Diffusion model의 이전 연구들에는 inference 중에 1~2천 개의 diffusion step이 필요하므로 큰 해상도 task의 경우 생성 속도가 느려진다. 보다 효율적인 inference를 가능하게 하기 위해 WaveGrad의 테크닉을 사용한다. 본 논문의 모델은 $\gamma$로 바로 컨디셔닝되며, diffusion step의 수와 inference 중 noise schedule을 유연하게 선택할 수 있다. 이것은 음성 합성에 잘 작동하는 것으로 입증되었지만 이미지에 대해서는 탐색되지 않았다. 저자들은 효율적인 inference를 위해 $T = 100$로 설정하고 inference noise schedule에 대한 hyper-parameter를 탐색하였다. PSNR이 이미지 품질과 잘 관련되지 않기 때문에 FID를 사용하여 최상의 noise schedule을 선택했다.
Experiments
- 데이터셋: FFHQ, CelebA-HQ, ImageNet 1K
- Training Details
- batch size 256
- 1M training step
- Adam optimizer
- Learning rate = $10^{-4}$ (10k step linear warmup)
1. Qualitative Results
Natural Images
다음은 ImageNet에서 학습한 SR3 model(64$\times$64 $\rightarrow$ 256$\times$256)을 ImageNet 테스트 이미지에서 평가한 것이다.

Face Images
다음은 FFHQ에서 학습한 SR3 model(64$\times$64 $\rightarrow$ 512$\times$512)을 학습 셋에 포함되지 않는 이미지에서 평가한 것이다.

2. Benchmark Comparison
Automated metrics
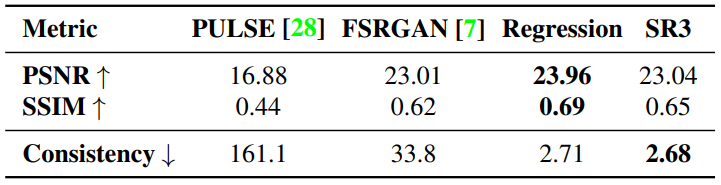
다음은 16$\times$16 $\rightarrow$ 128$\times$128 얼굴 super-resolution에 대한 PSNR과 SSIM을 평가한 것이다.
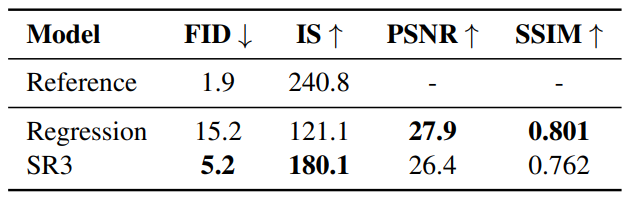
다음은 SR3와 Regression baseline을 ImageNet validation set으로 성능을 평가한 것이다.
다음은 ImageNet Validation set의 이미지 1,000개에서 4$\times$ 자연 이미지 super-resolution에 대한 classification 정확도를 비교한 것이다.

Human Evaluation (2AFC)
다음은 얼굴 super-resolution의 fool rates를 평가한 것이다.
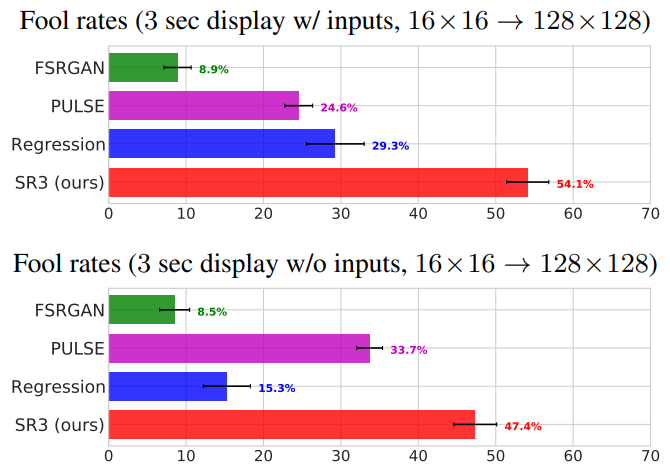
다음은 ImageNet super-resolution의 fool rates를 평가한 것이다.

3.Quantitative Results
다음은 16$\times$16 $\rightarrow$ 128$\times$128 얼굴 super-resolution task에 대한 다양한 방법을 비교한 것이다.

4. Cascaded High-Resolution Image Synthesis
다음은 unconditional 64$\times$64 diffusion model로 샘플링한 뒤 4$\times$ SR3 model 2개를 통과시켜 1024$\times$1024 얼굴 이미지를 생성한 것이다.

다음은 클래스 조건부 64$\times$64 diffusion model로 샘플링한 뒤 4$\times$ SR3 model을 통과시켜 256$\times$256 ImageNet 이미지를 생성한 것이다.

다음은 클래스 조건부 256$\times$256 ImageNet에 대한 FID 점수이다.

Ablation Studies
다음은 클래스 조건부 256$\times$256 ImageNet을 위한 SR model에 대한 ablation study 결과이다.
