[논문리뷰] Spherical Voronoi: Directional Appearance as a Differentiable Partition of the Sphere

arXiv 2025. [Paper] [Page]
Francesco Di Sario, Daniel Rebain, Dor Verbin, Marco Grangetto, Andrea Tagliasacchi
University of Torino | Simon Fraser University | University of British Columbia | University of Toronto | Google DeepMind
16 Dec 2025

Introduction

현재 SOTA novel view synthesis 방법들은 세밀한 텍스처와 복잡한 기하학적 디테일을 효과적으로 포착하는 데는 성공했지만, 광택 표면에 내재된 복잡하고 시점에 따라 달라지는 외형을 재현하는 데는 어려움을 겪는다. 따라서 추가적인 개선을 위해서는 radiance field의 방향 성분을 모델링하는 방식에 근본적인 변화가 필요하다.

Gaussian Splatting과 같이 렌더링 속도에 중점을 둔 접근 방식들은 Spherical Harmonics (SH)를 사용하여 view-dependent한 외형을 표현한다. SH는 계산 비용이 매우 저렴하여 효율적인 추론이 가능하며, 입력으로 제공되는 뷰 방향이 제한적일 경우 최적화가 더 용이하다. 그럼에도 불구하고, 주어진 주파수를 표현하는 데 필요한 계수의 수는 주파수 개수의 제곱에 비례하여 증가하므로, 반사광과 같은 날카로운 view-dependent한 효과를 정확하게 표현하기 어렵다.

반사를 렌더링하는 일반적인 접근 방식은 environment map으로 표현된 원거리 광원을 사용하거나, ray-tracing을 사용하여 근거리 광원이나 상호반사를 고려한다. 그러나 방출되는 radiance가 표면 normal에 크게 의존하기 때문에 추정된 geometry의 잠재적 오차에 매우 민감하여 최적화 문제를 야기한다. 이러한 최적화 어려움으로 인해 반사광이 없는 경우 반사를 명시적으로 모델링하지 않는 방법보다 성능이 떨어지는 경우가 많다.

본 논문에서는 구면을 셀로 적응적으로 분해하는 학습을 수행하는 Spherical Voronoi (SV)를 제안하였다. 이 근사 함수는 반사광과 같은 고주파 효과를 복원하는 동시에 sparse한 학습 환경에서도 안정적인 최적화를 지원한다. 또한, SV 표현은 SH나 spherical Gaussians (SG)와 같은 기존 방식보다 실제 데이터에서 파라미터 예산과 재구성 정확도 사이의 더 나은 trade-off를 제공한다.

Method

1. Background

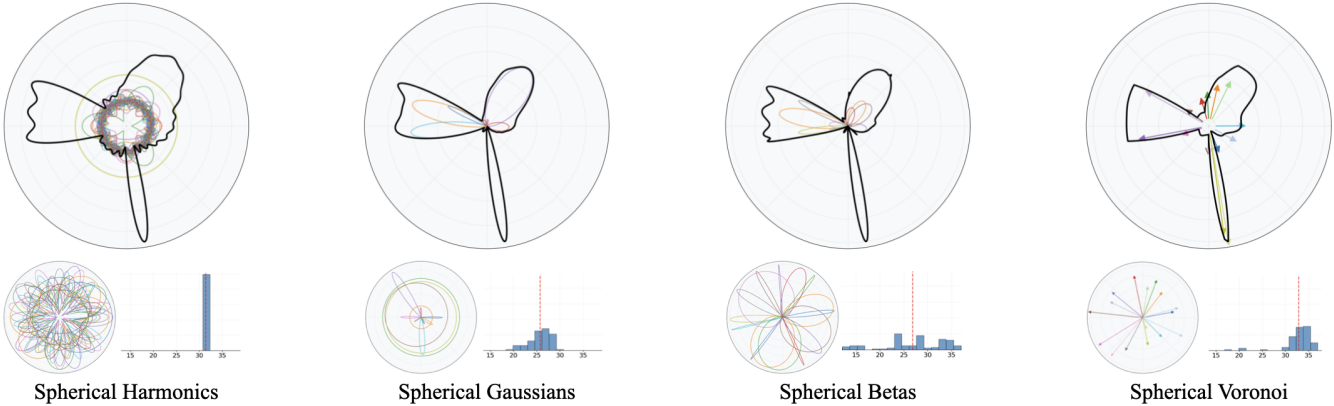
구면에서 정의된 함수 \(f: \mathbb{S}^2 \rightarrow \mathbb{R}^C\)는 다양한 spherical basis들을 사용하여 표현할 수 있다.

Spherical Harmonics (SH)

널리 사용되는 방법 중 하나는 Spherical Harmonics 전개이다.

\[\begin{equation} f_\textrm{SH} (\omega; c) = \sum_{l=0}^L \sum_{m=-l}^l c_{lm} Y_l^m (\omega) \end{equation}\]

$c_{lm} \in \mathbb{R}^C$은 최적화 가능한 계수이고, $Y_l^m$은 SH basis function이다. SH 최적화는 수치적으로 안정적이다. SH basis function은 orthonormal basis를 형성하며 글로벌하게 지원된다. 그러나 날카로운 로컬 고주파 신호를 포착하려면 많은 수의 basis function(큰 $L$)이 필요하며, 이는 파라미터 개수 증가와 함수의 불연속성을 표현할 때 Gibbs artifact의 발생이라는 두 가지 문제를 야기한다.

Spherical Gaussians (SG)

로컬 신호를 더 잘 모델링하기 위해 Spherical Gaussian들의 선형 결합을 사용할 수 있다.

\[\begin{equation} f_\textrm{SG} (\omega; \tau, s, c) = \sum_{k=1}^K c_k \exp (\tau_k (s_k \cdot \omega - 1)) \end{equation}\]

각 lobe는 평균 방향 $s_k$, concentration \(\tau_k\), amplitude $c_k$로 정의된다. SG는 함수를 부드럽고 회전 대칭적인 lobe들의 조합으로 설명한다. 그러나 SG lobe들의 조합은 초기화에 민감하고 최적화 과정에서 불안정한 경우가 많다. 이는 lobe의 정렬이 잘못되었을 때 약한 gradient를 초래하고, \(\tau_k\)가 클 경우 잘못된 업데이트를 유발한다.

Spherical Betas (SB)

Spherical Betas는 다음과 같이 정의되는 비대칭적인 bounded support lobe를 가능하게 함으로써 SG를 확장하였다.

\[\begin{equation} f_\textrm{SB} (\omega; \alpha, \beta, s) = \sum_{k=1}^K (1 + s_k \cdot \omega)^{\alpha_k - 1} (1 - s_k \cdot \omega)^{\beta_k - 1} \end{equation}\]

$s_k$는 principal direction이고, \(\alpha_k, \beta_k > 0\)는 모양을 제어한다. SB는 SG보다 유연하며, 왜곡되고 급격한 방향 변화를 모델링할 수 있다. 그러나 이러한 유연성 때문에 실제 최적화는 더 어렵다. SB의 기여도는 로컬하며, \(\alpha_k\)나 \(\beta_k\)의 극단적인 값은 매우 급격하고 평평한 영역을 생성하여 잘못된 gradient를 유발하고, SG보다 초기화에 훨씬 더 민감하다.

2. Spherical Voronoi (SV)

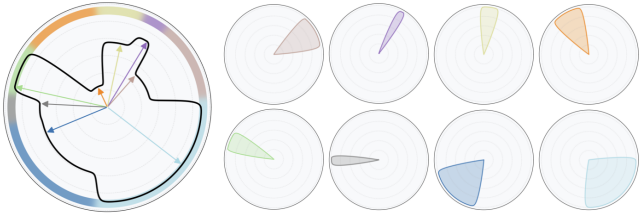
이러한 한계들을 극복하기 위해, 본 논문은 Spherical Voronoi (SV) 표현을 도입하였다. SV는 directional site $s_1, \ldots, s_K \in \mathbb{R}^2$와 관련 함수 값 $c_1, \ldots, c_K \in \mathbb{R}^C$의 집합으로 구성된다. 방향 $\omega$에서의 함수 평가는 각 site 값의 가중합으로 얻어진다.

\[\begin{equation} f_\textrm{SV} (\omega; \tau, s, c) = \sum_{k=1}^K w_k (\omega; \tau_k) c_k \\ \textrm{where} \quad w_k (\omega; \tau_k) = \frac{\exp (\tau_k s_k \cdot \omega)}{\sum_{k^\prime = 1}^K \exp (\tau_k s_{k^\prime} \cdot \omega)} \end{equation}\]

Temperature 파라미터 \(\tau_k > 0\)는 선명도를 제어한다. 작은 \(\tau_k\)는 부드러운 색상 전환을 생성하는 반면, 큰 \(\tau_k\)는 Voronoi tessellation에 가깝다. 모든 \(\tau_k\)가 동일한 값을 가질 때, 이 공식은 표준 soft Spherical Voronoi 모델에 해당하지만, 각 위치에 서로 다른 temperature를 할당하면 로컬하게 적응하는 선명도를 갖는 변형으로 자연스럽게 확장된다. \(\tau_k\)를 조정함으로써 모델은 부드러운 신호와 날카로운 신호를 모두 효과적으로 표현할 수 있다.

Softmax function은 ​​모든 위치에 대해 잘 정의된 gradient를 보장하고, temperature를 통해 표현의 선명도를 조정할 수 있으며, 결과적으로 생성되는 분할은 SG나 SB와 같은 표현에서 나타나는 겹치는 커널 간의 경쟁을 방지하는 깨끗하고 겹치지 않는 구면의 분해를 유도한다.

3. View-direction parameterization

고전적인 radiance field 학습을 위해, 저자들은 view-dependent한 표현을 SV로 대체하였다. 뷰 방향 $\omega$가 주어지면, primitive와 관련된 radiance는 \(f_\textrm{SV}\)로 평가되며, 함수의 공역은 RGB 색상이다. 3DGS의 경우, 이는 각 Gaussian에 추가 파라미터 \(\{\tau_k\}\), \(\{s_k\}\), \(\{c_k\}\)가 부여됨을 의미하며, 모든 파라미터는 학습 가능하고 공동으로 최적화된다.

4. Reflection-based Parameterization

Ref-NeRF는 광택 표면에서 뷰 방향을 이용하여 방출되는 radiance를 계산할 때 sparse한 측정값으로부터 복잡한 함수를 학습해야 한다는 점을 보여주었다. 그 대신 표면의 normal 벡터 $n$을 함께 학습하고, 반사된 뷰 방향을 따라 측정된 radiance \(\omega_r = 2 (\omega \cdot n) n − \omega\)라는 더 간단한 함수를 사용하여 추론하는 방법을 제안했다.

SV 함수는 표현력이 풍부하며, 특히 날카로운 조명 영역을 표현하는 데 매우 적합하다. 따라서 SV 함수는 부드러운 view-dependent한 효과 $f(\omega)$를 표현하는 데 적합할 뿐만 아니라 미세한 반사광 \(f(\omega_r)\)을 학습하는 데에도 적합하다.

Learnable light probes

\(f(\omega_r)\)에만 의존하는 것은 원거리 조명을 가정하는 것인데, 이는 실제 상황에서는 잘못된 모델이다. 특히 광택 있는 물체가 다른 물체나 광원 근처에 있을 때, 외형이 방향뿐 아니라 위치에도 영향을 받기 때문에 문제가 된다. 이를 위해 Ref-NeRF는 NeRF를 반사 방향과 위치 모두로 컨디셔닝했다. 그러나 Gaussian splat과 같은 명시적 표현으로 3D 장면을 표현할 경우, 이러한 방식을 구현하기가 훨씬 어려워진다.

이러한 한계를 극복하기 위해, 저자들은 장면 전체에 배치된 학습 가능한 light probe 세트를 도입하였다. 각 probe는 로컬한 reflection field를 인코딩하며, 들어오는 radiance의 간결한 표현을 저장하므로, 렌더링 시스템은 주변 probe의 기여도를 interpolation하여 공간적으로 변화하는 조명을 근사할 수 있다.

Deferred Rendering with Voronoi Light Probes

저자들은 3DGS-DR을 따라 geometry와 조명을 분리하는 deferred rendering 전략을 채택하였다. 2DGS backbone을 기반으로 프레임워크를 구축하고, 각 Gaussian에 두 개의 추가적인 학습 가능한 material 파라미터, 즉 roughness 값 $r \in [0, 1]$과 diffuse color $d \in \mathbb{R}^3$를 추가하였다.

Geometry pass에서 모든 2D Gaussian은 한 번 rasterization되어 각 이미지 좌표에 대한 buffer를 생성하며, 이 buffer에는 보이는 표면의 3D 위치 $P$, normal $N$, roughness $R$, diffuse color $D$가 저장된다. 주어진 픽셀의 최종 색상은 다음과 같이 계산된다.

\[\begin{equation} C = D + C_\textrm{spec} \end{equation}\]

\(C_\textrm{spec}\)은 반사광 성분을 인코딩한다. 반사광 색상은 근거리 조명과 원거리 조명 사이의 혼합으로 모델링된다.

\[\begin{equation} C_\textrm{spec} = \alpha C_n + (1 - \alpha) C_f \end{equation}\]

원거리 항 $C_f$는 원거리 조명을 나타내며 반사 방향 \(\omega_r = 2(\omega \cdot N)N − \omega\)에서 평가되는 학습 가능한 cubemap으로 구현된다.

근거리 항 $C_n$은 학습 가능한 Voronoi light probe들을 사용하여 공간적으로 변화하는 반사를 포착한다. 각 probe $i$는 위치 $p_i \in \mathbb{R}^3$, 혼합 가중치 \(\alpha_i \in [0, 1]\), 그리고 SV 함수의 파라미터(\(\tau_i\), $s_i$, $c_i$)로 parameterize된다. 모든 파라미터는 학습 중에 최적화된다. 표면 위의 점 $P$에 대해, 해당 점의 $k$개의 가장 가까운 probe를 쿼리하고, inverse-distance weight을 계산한다.

\[\begin{equation} \tilde{w}_i = \frac{\| P - p_i \|^{-1}}{\sum_{j \in \mathcal{N}} \| P - p_j \|^{-1}} \textrm{where} \quad \mathcal{N} = \textrm{kNN}(P) \end{equation}\]

근거리 색상 및 혼합 계수는 다음과 같이 계산된다.

\[\begin{equation} C_n = \sum_{i \in \mathcal{N}} \tilde{w}_i f_\textrm{SV}^i (\omega_r; \tau), \quad \alpha = \sum_{i \in \mathcal{N}} \tilde{w}_i \alpha_i \end{equation}\]

여기서 roughness $R$은 temperature $\tau$를 조절하며, 이 temperature는 SV 분포의 선명도를 제어한다.

\[\begin{equation} \tau = (1 - R) \tau_\textrm{max} + R \tau_\textrm{min} \end{equation}\]

(\(\tau_\textrm{max}\)와 \(\tau_\textrm{min}\)은 고정된 hyperparameter)

Roughness가 낮은 영역은 $\tau$ 값이 높아져 더 선명한 반사를 생성하고, roughness가 높을수록 반사 폭이 넓어진다. 이 반사 기반 공식에서 $\tau$는 직접 학습되는 것이 아니라 roughness $R$로부터 도출된다.

Experiments

1. View Direction Parameterization

2. Reflection-based Parameterization

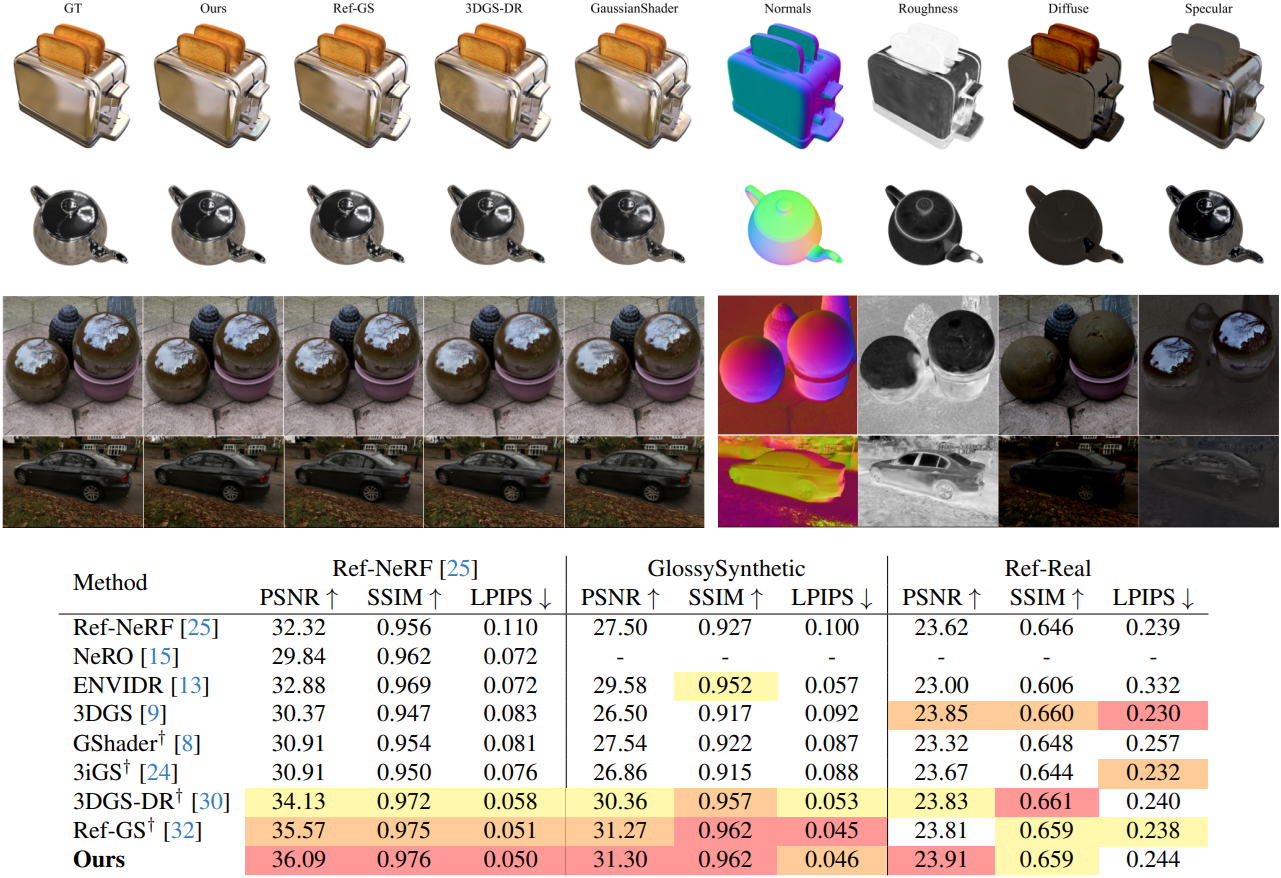
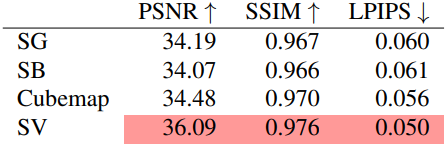
3. Ablations

4. Train and Inference Time