[논문리뷰] No Pose at All: Self-Supervised Pose-Free 3D Gaussian Splatting from Sparse Views

ICCV 2025 (Highlight). [Paper] [Page] [Github]
Ranran Huang, Krystian Mikolajczyk
Imperial College London
2 Aug 2025

Introduction

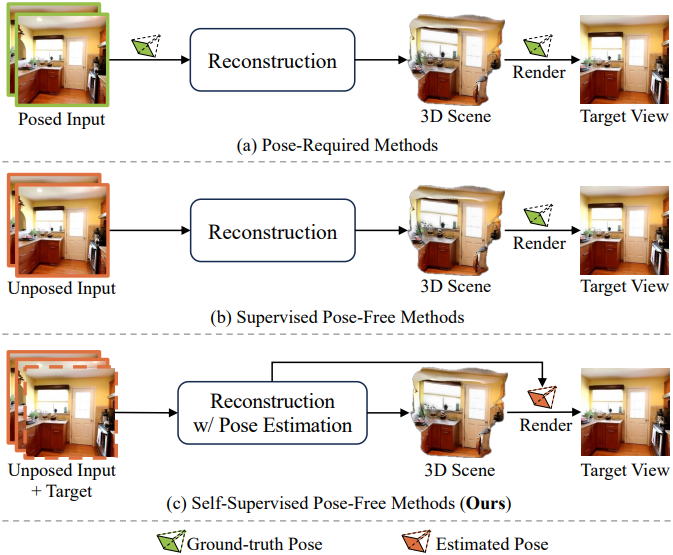
기존의 pose-free 방법은 포즈가 없는 이미지로부터 3D 장면을 재구성하며, inference 단계에서 알려진 입력 시점 포즈를 필요로 하지 않지만, 새로운 시점에서의 실제 포즈를 기반으로 렌더링 loss를 사용하여 학습한다. 따라서 이러한 접근법은 supervised pose-free 기법으로 분류한다. 결과적으로, 이러한 방법들의 학습은 알려진 카메라 포즈를 가진 데이터셋에 국한되어, 포즈 주석이 없는 대규모 실제 데이터로의 확장성이 제한된다.

이는 3D 장면 학습 중 새로운 뷰의 GT 포즈가 정말로 필수적인지에 대한 질문을 제기한다. 한 가지 해결책은 모델에서 추정된 포즈를 사용하여 3D 장면을 최적화하는 것인데, 이는 self-supervised pose-free 패러다임이라고 한다. 그러나 이 방법은 렌더링 loss가 3D geometry와 카메라 포즈 학습을 본질적으로 결합하기 때문에 포즈 오치가 재구성 품질을 저하시키고, 이는 포즈 추정을 더욱 어렵게 만든다. 이러한 상호 의존성은 잠재적으로 불안정한 학습 또는 심지어 발산으로 이어질 수 있는 피드백 루프를 생성한다. 최근의 self-supervised pose-free 접근법은 장면 재구성과 포즈 추정에 별도의 모듈을 사용하여 두 task에서 일관된 feature 표현을 학습하는 것을 저해하고 기하학적 정렬을 저해하기 때문에 이 문제를 완화하는 데 어려움을 겪는다. 결과적으로 이러한 방법들은 ​​포즈가 필요한 방법이나 supervised pose-free 방법에 비해 여전히 크게 뒤떨어져 있다.

본 논문은 이를 해결하기 위해, sparse view들로부터 3DGS를 위한 self-supervised pose-free 접근법인 SPFSplat을 소개한다. 이 접근법에서는 학습 과정에서 주어진 타겟 이미지를 기반으로 새로운 시점의 포즈를 추정한다. SPFSplat은 feature 추출을 위해 공유 백본을 사용하며, 3D Gaussian과 카메라 포즈를 예측하는 전용 head를 갖추고 있다. 이 통합 아키텍처는 계산 효율성을 향상시킬 뿐만 아니라 장면 재구성 및 포즈 추정을 위한 공동 feature 학습을 용이하게 하여 기하학적 일관성을 개선하고 불안정한 피드백 루프를 완화한다.

이는 3D geometry가 정확한 카메라 정렬의 이점을 활용하고, 포즈 예측이 상호 강화의 한 형태로 글로벌 장면 컨텍스트를 활용할 수 있도록 함으로써 달성된다. 또한, 레퍼런스 시점을 기준으로 3D Gaussian을 직접 예측하여 포즈 오차가 장면의 geometry에 미치는 영향을 줄였다. 또한 예측된 Gaussian을 해당 이미지 픽셀에 명시적으로 맞춰 렌더링 loss를 보완하고, 더 강력한 기하학적 제약을 적용하여 학습 안정성을 향상시켰다.

Method

1. Problem Formulation

본 논문에서는 포즈가 없는 $N$개의 입력 이미지 \(\{\textbf{I}^v\}_{v=1}^N\)로부터 3D Gaussian을 재구성하는 동시에 카메라 포즈를 추정하는 feed-forward 네트워크를 학습하는 것을 목표로 한다. 학습 과정에서, 타겟 시점 $t$에서 추정된 포즈로부터 사실적인 이미지 \(\hat{\textbf{I}}^t\)를 합성하여 3D Gaussian을 최적화함으로써, 실제 포즈가 필요 없게 된다.

3D Gaussian Reconstruction

Splatt3R와 NoPoSplat을 따라, 첫 번째 입력 시점 $\textbf{I}^1$이 글로벌 레퍼런스 좌표계로 사용되는 3D 공간에서 3D Gaussian을 예측한다.

\[\begin{equation} f_\theta = \{ \textbf{I}^v \}_{v=1}^N \mapsto \{ \boldsymbol{\mathcal{G}}^{v \rightarrow 1} \}_{v = 1, \ldots, N} \\ \textrm{where} \quad \boldsymbol{\mathcal{G}}^{v \rightarrow 1} = \{ (\boldsymbol{\mu}_j^{v \rightarrow 1}, \textbf{r}_j^{v \rightarrow 1}, \textbf{c}_j^{v \rightarrow 1}, \alpha_j^{v \rightarrow 1}, \textbf{s}_j^{v \rightarrow 1}) \}_{j = 1, \ldots, H \times W} \end{equation}\]

(\(\boldsymbol{\mathcal{G}}^{v \rightarrow 1}\)는 $\textbf{I}^1$의 좌표계로 표현된 $\textbf{I}^v$의 픽셀 정렬된 Gaussian, \(\boldsymbol{\mu} \in \mathbb{R}^3\)는 center, $\textbf{r} \in \mathbb{R}^4$는 rotation quaternion, $\textbf{s} \in \mathbb{R}^3$는 scale, $\alpha \in \mathbb{R}$는 opacity, $\textbf{c} \in \mathbb{R}^k$는 spherical harmonics (SH))

Pose Estimation

시점 $\textbf{I}^v$에서 레퍼런스 시점 $\textbf{I}^1$로의 상대적 변환을 추정하기 위해 포즈 네트워크 \(f_\phi\)를 도입하였다.

\[\begin{equation} \textbf{P}^{v \rightarrow 1} = [\textbf{R}^{v \rightarrow 1} \vert \textbf{T}^{v \rightarrow 1}] = f_\phi (\textbf{I}^v, \textbf{I}^1) \end{equation}\]

($\textbf{R}^{v \rightarrow 1} \in \mathbb{R}^{3 \times 3}$은 rotation 행렬, $\textbf{T}^{v \rightarrow 1} \in \mathbb{R}^{3 \times 1}$는 translation 벡터)

Novel View Synthesis

학습 과정에서, 타겟 시점에서 이미지 합성을 위한 실제 포즈에 대한 의존성을 제거하기 위해, $\textbf{I}^t$에서 $\textbf{I}^1$로의 상대적 포즈를 추정한다. 추정된 변환을 사용하여 새로운 시점에서 이미지를 렌더링한다.

\[\begin{equation} \hat{\textbf{I}}^t = \mathcal{R}(\textbf{P}^{t-1}, \{ \boldsymbol{\mathcal{G}}^{v \rightarrow 1} \}_{v = 1, \ldots, N}) \end{equation}\]

Intrinsic 파라미터는 카메라 센서 메타데이터에서 사용 가능하다고 가정한다.

2. Architecture

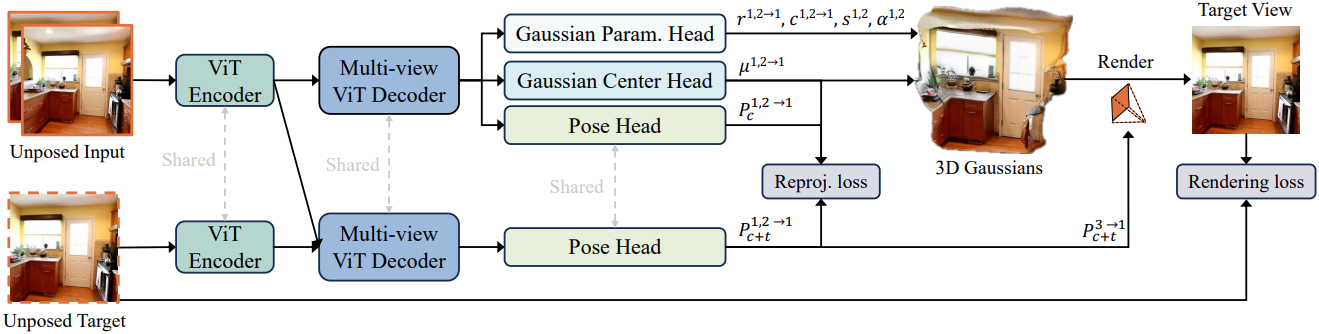
아키텍처는 인코더, 디코더, 포즈 head, Gaussian 예측 head로 구성된다. 인코더와 디코더는 모두 ViT 아키텍처를 기반으로 한다.

Encoder and Decoder

각 입력 시점에 대해 RGB 이미지는 먼저 patchify되고 일련의 이미지 토큰으로 flatten된다. 그런 다음, 스케일 모호성을 완화하기 위해 linear layer를 사용하여 intrinsic 파라미터를 추가 토큰으로 인코딩한 다음, 이 토큰을 공간 차원을 따라 이미지 토큰과 concat한다. 이 연산은 선택 사항이며, intrinsic 파라미터를 backbone에 삽입하지 않고도 기존 접근 방식을 능가한다.

각 시점의 토큰은 먼저 가중치가 공유된 ViT 인코더에 의해 개별적으로 처리된다. 그런 다음, cross-attention을 갖춘 ViT 디코더가 멀티뷰 정보를 집계한다. 디코더는 모든 입력 시점에 걸쳐 토큰 표현을 공동으로 추론하며, 각 시점은 다른 모든 시점에 attention되어 시점 사이의 정보 교환을 촉진하여 공간적 관계와 글로벌한 3D geometry를 포착한다. 이 접근 방식은 메모리나 계산 비용을 크게 증가시키지 않고도 추가 입력 시점을 효율적으로 통합할 수 있도록 지원한다.

Gaussian Prediction Heads

Splatt3R와 NoPoSplat을 따라, 두 개의 DPT 기반 head를 사용하여 Gaussian 파라미터를 추론한다. 첫 번째 head는 컨텍스트 뷰에서 디코더 토큰을 처리하고 각 픽셀의 3D 좌표를 예측하여 Gaussian 중심을 정의한다. 두 번째 head는 각 Gaussian에 대한 rotation, scale, 불투명도, SH 계수를 추정한다. 원본 입력 이미지를 예측 head에 입력하여 고해상도 skip connection들을 통합하고, 세밀한 공간적 디테일을 보존한다.

Pose Head

포즈 head는 한 번의 feed-forward step으로 입력 뷰에 대한 포즈를 예측할 수 있도록 하며, Gaussian의 self-supervised learning에 필수적이다. Gaussian head와 동일한 디코더를 기반으로 구축되어 기하학적 지식 공유와 Gaussian과 포즈 간의 더 나은 정렬을 촉진한다.

포즈 head 내에서 인코더와 디코더의 토큰 표현은 concat, unpatchify, global average pooling을 통해 처리되어 각 뷰에 대한 컴팩트한 geometry 임베딩을 생성한다. 이 임베딩은 가벼운 3-layer MLP에 공급되고, 이 MLP는 카메라 포즈를 10차원 표현으로 직접 출력한다.

포즈는 각 뷰에 대한 translation과 rotation으로 분해된다. Translation은 4개의 homogeneous coordinate를 사용하여 표현되고, rotation은 6D 형식으로 인코딩되어 두 개의 정규화되지 않은 좌표 축을 캡처한다. 이러한 축은 정규화되고 외적 연산을 통해 결합되어 전체 rotation 행렬을 구성한다. 레퍼런스 뷰에 대한 상대적 포즈를 계산하기 위해 10D 포즈 표현은 homogeneous transformation matrix $\textbf{P}^{v \rightarrow 1} \in \mathbb{R}^{4 \times 4}$로 변환된다. 첫 번째 입력 뷰에 $[\textbf{U} \vert \textbf{0}]$를 할당하여 카메라 포즈를 정규화한다 ($\textbf{U}$는 단위 행렬, $\textbf{0}$은 영벡터).

학습 과정에서, GT 포즈 없이 타겟 뷰에서 이미지 합성을 가능하게 하기 위해, 컨텍스트 뷰와 타겟 뷰를 모두 포함하는 context-with-target branch를 추가로 도입한다. 이러한 뷰의 인코더 토큰은 멀티뷰 ViT 디코더에 의해 공동으로 집계된 후, 포즈 head를 통해 타겟 포즈가 예측된다.

중요한 점은 정보 유출을 방지하기 위해 Gaussian 재구성과 타겟 포즈 예측이 분리된다는 것이다. Gaussian 표현은 컨텍스트 뷰에서만 예측되는 반면, 타겟 포즈 추정은 컨텍스트 뷰와 타겟 뷰 모두의 정보를 활용하여 글로벌 geometry를 더욱 포괄적으로 이해한다. 이러한 디자인은 타겟 뷰의 정보가 3D Gaussian 표현에 영향을 미치지 않도록 하여 새로운 뷰에 대한 일반화를 향상시킨다.

3. Loss Function

Image Rendering Loss

본 모델은 실제 RGB 이미지를 사용하여 학습된다. 학습 loss는 L2 loss와 LPIPS loss의 가중 합이다.

\[\begin{equation} \mathcal{L}_\textrm{render} = \| \textbf{I}^t - \hat{\textbf{I}}^t \|_2 + \gamma \textrm{LPIPS}(\textbf{I}^t, \hat{\textbf{I}}^t) \end{equation}\]

($\textbf{I}^t$는 GT 이미지, $\hat{\textbf{I}}^t$는 렌더링된 이미지)

Reprojection Loss

기존 접근법은 입력 viewing ray를 따라 Gaussian 위치를 제한함으로써 픽셀 정렬된 Gaussian 예측을 강화한다. 반면, canonical space 기반 방법들은 Gaussian 중심을 가이드하기 위해 GT 카메라 포즈에 의존한다. 두 전략 모두 각 픽셀과 해당 3D 포인트 간의 정렬을 보장한다. 그러나 본 모델은 알려진 카메라 포즈 없이 canonical space에서 3D Gaussian 중심을 학습하기 때문에, 네트워크에는 픽셀 정렬된 Gaussian 표현을 강화하기 위한 명시적인 기하학적 제약 조건이 없다.

단순한 해결책은 컨텍스트 뷰에서 이미지를 합성하고 실제 이미지와 비교하여 loss를 계산하는 것이다. 그러나 이는 overfitting으로 인해 학습이 불안정해진다. 네트워크가 첫 번째 컨텍스트 뷰의 렌더링 품질 향상을 우선시하는데, 3D Gaussian 공간이 카메라 좌표로 정의되어 렌더링이 학습 가능한 포즈와 독립적으로 이루어지기 때문이다. 이 뷰의 Gaussian은 이미 충분한 장면 정보를 포착하고 있기 때문에, 모델은 다른 컨텍스트 뷰의 Gaussian 중심을 이동시키고 카메라 포즈를 조정하여 다른 뷰의 기여를 억제하고, 궁극적으로 학습 붕괴를 초래한다.

이 문제를 해결하기 위해, pixel-wise reprojection loss를 사용하여 3D 포인트와 카메라 포즈를 공동으로 최적화한다. 이미지 기반 loss와 달리, reprojection loss는 명시적인 기하학적 제약 조건을 적용하여 컨텍스트 뷰에 대한 overfitting을 줄인다.

구체적으로, 컨텍스트 뷰 $v$에 있는 각 픽셀 \(\textbf{p}_j^v\)에 대해, 첫 번째 카메라 좌표계에서 추정된 뷰 $v$의 포즈를 사용하여 3D Gaussian 중심 \(\boldsymbol{\mu}_j^{v \rightarrow 1}\)를 2D 픽셀 좌표로 projection시키고 pixel-wise reprojection error를 최소화한다. 학습 과정에서 context-only branch와 context-with-target branch 모두에서 컨텍스트 포즈를 얻을 수 있으므로, 두 가지 모두에 reprojection loss를 적용하여 일관성을 강화한다.

\[\begin{equation} \mathcal{L}_\textrm{reproj} = \sum_{v=1}^N \sum_{j=1}^{H \times W} \| \textbf{p}_j^v - \pi (\textbf{K}^v, \textbf{P}^{v \rightarrow 1}, \boldsymbol{\mu}_j^{v \rightarrow 1}) \| \\ \textrm{where} \quad \textbf{P}^{v \rightarrow 1} \in \{ \textbf{P}_c^{v \rightarrow 1}, \textbf{P}_{c+t}^{v \rightarrow 1} \} \end{equation}\]

($\pi$는 projection 함수, $\textbf{K}^v$는 시점 $v$의 intrinsic, \(\textbf{P}_c^{v \rightarrow 1}\)는 context-only branch에서 추정된 상대적 포즈, \(\textbf{P}_{c+t}^{v \rightarrow 1}\)는 context-with-target branch에서 추정된 상대적 포즈)

Reprojection loss를 활용함으로써, 실제 카메라 포즈 없이도 픽셀 정렬된 3D Gaussian 이미지의 안정적인 학습과 효율적인 최적화를 가능하게 한다.

Experiments

• 데이터셋: RealEstate10K (RE10K), ACID
• 구현 디테일
  • GPU: A100 1개
  • 인코더: ViT-Large
  • 디코더: ViT-Base
  • 초기화
    • 인코더, 디코더, Gaussian 중심 head: MASt3R 가중치
    • 포즈 head: identity rotation matrix를 근사하도록
    • 나머지는 랜덤 초기화
  • 가중치
    • LPIPS: 0.05
    • reprojection: 0.001
  • 해상도: 256$\times$256

1. Results

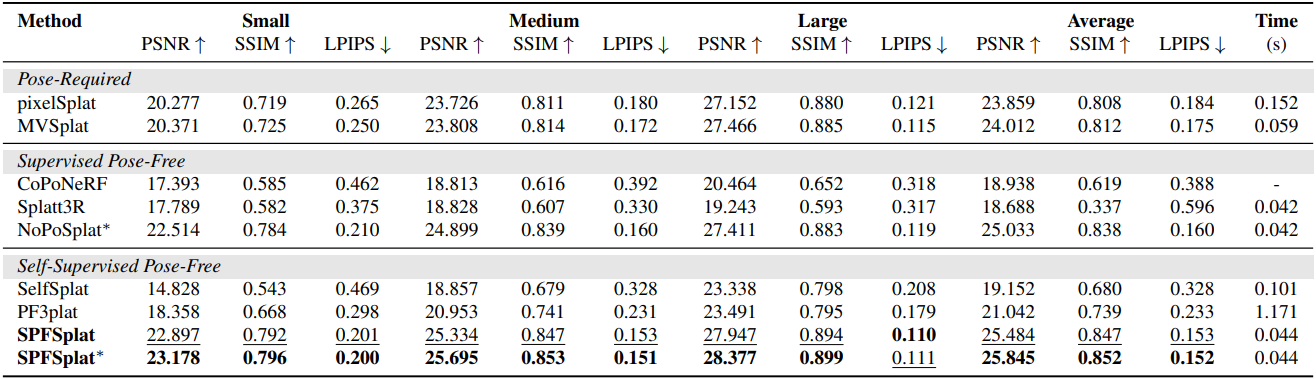
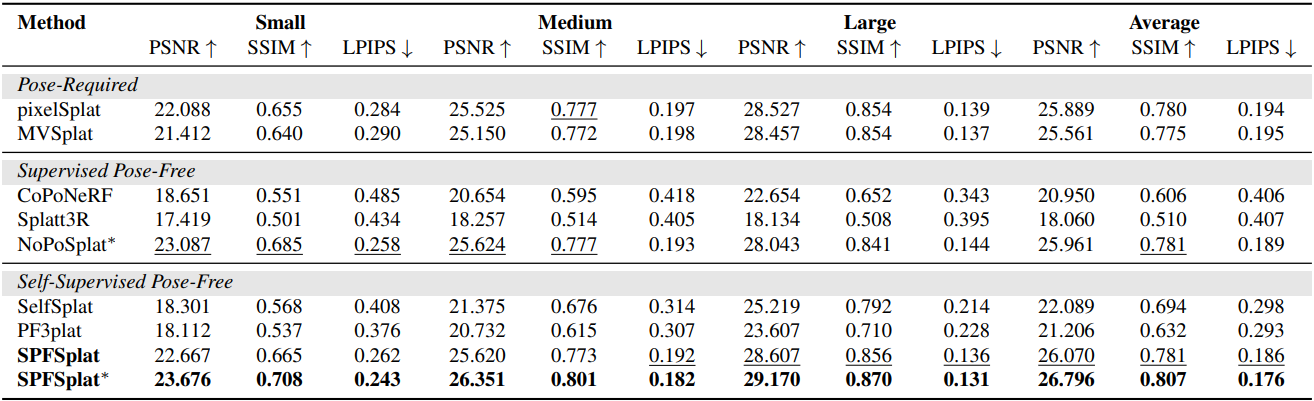
다음은 RE10K에서의 novel view synthesis 성능을 비교한 결과이다.

다음은 ACID에서의 novel view synthesis 성능을 비교한 결과이다.

다음은 RE10K와 ACID에서의 정성적 비교 결과이다.

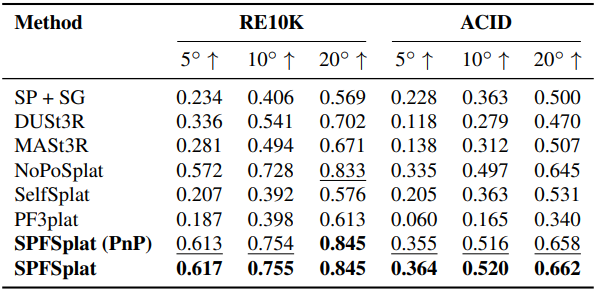
다음은 포즈 추정 성능을 비교한 결과이다.

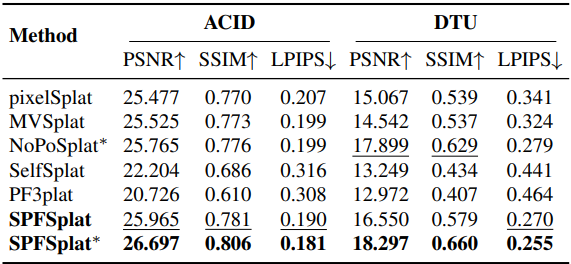
다음은 데이터셋 사이의 일반화 성능을 비교한 결과이다.

(위: RE10K → ACID / 아래: RE10K → DTU)

다음은 3D Gaussian과 렌더링 결과를 비교한 예시들이다.

2. Ablation Analysis

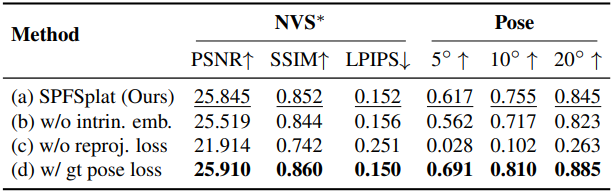
다음은 구성 요소에 대한 ablation 결과이다. (RE10K)

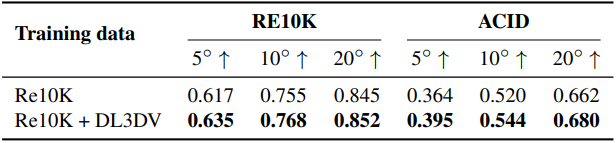
다음은 학습 데이터 크기에 대한 ablation 결과이다.

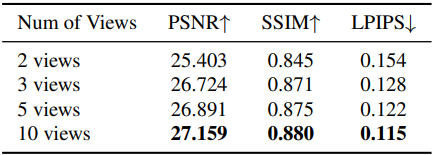
다음은 입력 뷰 수에 따른 성능을 비교한 결과이다.