[논문리뷰] Spec-Gaussian: Anisotropic View-Dependent Appearance for 3D Gaussian Splatting
NeurIPS 2024. [Paper] [Page] [Github]
Ziyi Yang, Xinyu Gao, Yangtian Sun, Yihua Huang, Xiaoyang Lyu, Wen Zhou, Shaohui Jiao, Xiaojuan Qi, Xiaogang Jin
Zhejiang University | The University of Hong Kong | ByteDance Inc.
24 Feb 2024

Introduction
AR/VR, 3D 콘텐츠 제작, 예술 작품 제작과 같은 다양한 응용 분야에서는 이미지 컬렉션의 고품질 재구성과 사실적인 렌더링이 매우 중요하다. 고전적인 방법은 메쉬나 점과 같은 기본 표현을 사용하고 최신 GPU에 최적화된 rasterization 파이프라인을 활용하여 실시간으로 렌더링한다. 대조적으로, NeRF는 implicit한 표현을 활용하여 연속적인 장면 표현을 제공하고 볼륨 렌더링을 사용하여 렌더링 결과를 생성한다. 이 접근 방식을 사용하면 장면 디테일을 강화하고 장면 형상을 보다 효과적으로 재구성할 수 있다.
최근에는 3D Gaussian Splatting(3D-GS)이 SOTA 품질과 실시간 속도를 제공하는 선도적인 기술로 등장했다. 이 방법은 3D 장면의 모양과 형상을 동시에 캡처하는 3D Gaussian의 집합을 최적화하여 디테일을 보존하고 고품질 결과를 생성하는 연속적인 표현을 제공한다. 또한 3D Gaussian을 위한 CUDA 맞춤형 미분 가능한 rasterization 파이프라인을 통해 고해상도에서도 실시간 렌더링이 가능하다.
탁월한 성능에도 불구하고 3D-GS는 장면 내의 specular(정반사) 성분을 모델링하는 데 어려움을 겪는다. 이 문제는 주로 이러한 시나리오에 필요한 고주파수 정보를 캡처하는 차수가 낮은 spherical harmonics(SH)의 제한된 능력에서 비롯된다. 결과적으로 이는 3D-GS가 specular 성분이 있는 장면을 모델링하는 데 어려움을 겪는다.
본 논문은 이 문제를 해결하기 위해 비등방성(anisotropic)과 specular 성분 모델링을 위한 anisotropic spherical Gaussian (ASG), 가속 및 저장공간 감소를 위한 앵커 기반 geometry-aware 3D Gaussian, floater를 제거하고 학습 효율성을 향상시키는 효과적인 학습 메커니즘을 결합한 Spec-Gaussian이라는 새로운 접근 방식을 도입한다. 구체적으로 이 방법은 세 가지 주요 디자인을 통합한다.
- 각 3D Gaussian의 모양을 모델링하기 위해 SH 대신 ASG appearance field를 활용하는 새로운 3D Gaussian 표현: 차수가 낮은 ASG는 차수가 낮은 SH가 할 수 없는 고주파수 정보를 효과적으로 모델링할 수 있다. 이 새로운 디자인을 통해 3D-GS는 정적 장면에서 비등방성과 specular 성분을 보다 효과적으로 모델링할 수 있다.
- 하위 Gaussian의 위치와 표현을 제어하기 위해 sparse한 앵커 포인트를 사용하는 하이브리드 접근 방식: 이 전략을 사용하면 계층적이고 형상을 인식하는 포인트 기반 장면 표현이 가능하며 앵커 Gaussian만 저장하면 되므로 저장공간 요구량이 크게 줄어들고 형상이 향상된다.
- Floater를 제거하고 학습 효율성을 높이도록 3D-GS에 맞게 특별히 맞춤화된 coarse-to-fine 학습 방식. 이 전략은 초기 단계에서 저해상도 렌더링을 최적화하여 3D Gaussian 수를 늘릴 필요를 방지하고 학습 프로세스를 정규화하여 floater로 이어지는 불필요한 기하학적 구조의 생성을 방지함으로써 학습 시간을 효과적으로 단축한다.
Spec-Gaussian은 이러한 디자인들을 결합함으로써 Gaussian의 효율성을 유지하면서 specular highlight와 비등방성에 대한 고품질 결과를 렌더링할 수 있다. 또한 Spec-Gaussian은 3D-GS에 specular highlight를 모델링할 수 있는 능력을 부여할 뿐만 아니라 일반적인 벤치마크에서 SOTA 결과를 달성하였다.
Method
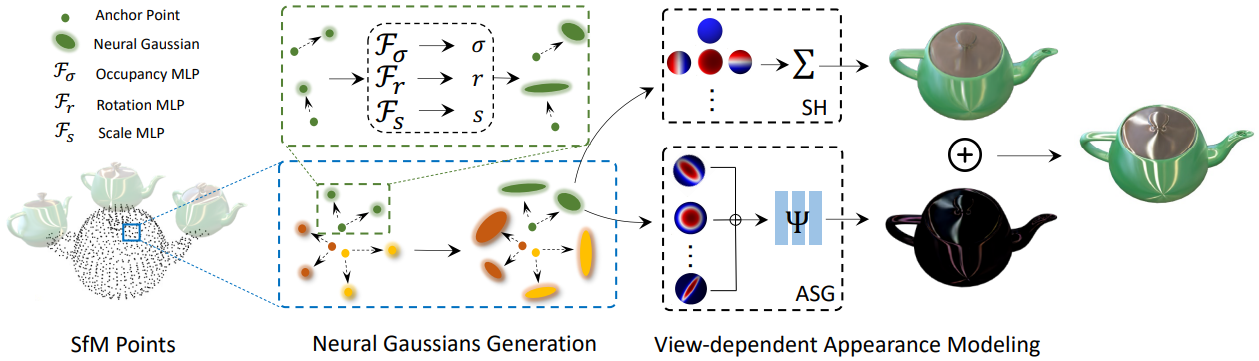
본 논문의 방법의 개요는 위 그림에 설명되어 있다. 모델에 대한 입력은 SfM에서 얻은 sparse한 포인트 클라우드와 포즈를 아는 정적 장면의 이미지 집합이다. 본 논문의 방법의 핵심은 3D Gaussian의 모양을 모델링할 때 SH를 대체하기 위해 ASG appearance field를 사용하는 것이다. 저자들은 ASG에 의해 도입된 저장공간 및 렌더링 속도의 압력을 줄이기 위해 sparse한 앵커 Gaussian을 사용하는 하이브리드 Gaussian 모델을 설계하였다. 마지막으로, 실제 장면에서 floater를 줄이기 위한 간단하면서도 효과적인 coarse-to-fine 학습 전략을 도입하였다.
1. Preliminaries
Anisotropic Spherical Gaussian
Anisotropic spherical Gaussian (ASG)는 조명과 shading을 효율적으로 근사화하기 위해 기존 렌더링 파이프라인 내에서 설계되었다. Spherical Gaussian (SG)와 달리 ASG는 상대적으로 적은 수로 비등방성 장면을 효과적으로 표현하는 것으로 입증되었다. SG의 기본 특성을 유지하는 것 외에도 ASG는 rotational invariance를 가지며 전체 주파수 신호를 나타낼 수 있다. ASG 함수는 다음과 같이 정의된다.
\[\begin{equation} \textrm{ASG} (\nu \; \vert \; [\mathbf{x}, \mathbf{y}, \mathbf{z}], [\lambda, \mu], \xi) = \xi \cdot \textrm{S} (\nu; \mathbf{z}) \cdot \exp (-\lambda (\nu \cdot \mathbf{x})^2 - \mu (\nu \cdot \mathbf{y})^2) \\ \textrm{where} \quad \mathbf{S}(\nu; \mathbf{z}) = \max (\nu \cdot \mathbf{z}, 0) \end{equation}\]여기서 $\nu$는 함수 입력으로 사용되는 단위 방향이며, $\mathbf{x}$, $\mathbf{y}$, $\mathbf{z}$는 각각 tangent, bi-tangent, lobe axis에 해당하고 서로 직교한다. $\lambda \in \mathbb{R}$과 $\mu \in \mathbb{R}$은 $\mathbf{x}$축과 $\mathbf{y}$축에 대한 sharpness 파라미터이며 $\lambda, \mu > 0$을 만족한다. $\xi \in \mathbb{R}^2$은 lobe amplitude이다.
복잡한 비등방성이 있는 장면 모델링에서 ASG의 강력한 능력에 영감을 받아 ASG를 Gaussian Splatting에 통합하여 클래식 모델의 힘과 새로운 렌더링 파이프라인을 결합하여 더 높은 품질을 제공한다. $N$개 ASG에 대하여 orthonormal axes $\mathbf{x}$, $\mathbf{y}$, $\mathbf{z}$를 미리 정의하여 반구에 균일하게 분포되도록 초기화한다. 학습 중에 나머지 ASG 파라미터인 $\lambda$, $\mu$, $\xi$를 학습할 수 있도록 한다. 뷰에 따른 반사 정보를 모델링하기 위해 ASG를 쿼리하기 위한 입력으로 반사 방향 $\omega_r$을 사용한다. 각 3D Gaussian에 대해 $N = 32$개의 ASG를 사용한다.
2. Anisotropic View-Dependent Appearance
ASG Appearance Field for 3D Gaussians
SH가 뷰에 따른 장면 모델링을 가능하게 했지만, 차수가 낮은 SH의 저주파수로 인해 specular highlight와 비등방성 효과와 같은 복잡한 광학 현상이 있는 장면을 모델링하기가 어렵다. 따라서 SH를 사용하는 대신 ASG appearance field를 사용하여 각 3D Gaussian의 모양을 모델링한다. 그러나 ASG를 도입하면 각 3D Gaussian의 feature 크기가 증가하여 모델의 저장공간 오버헤드가 증가한다. 이 문제를 해결하기 위해 $N$개의 ASG에 대한 파라미터를 예측하기 위해 소형의 학습 가능한 MLP $\Theta$를 사용하며, 각 Gaussian은 MLP에 대한 입력으로 추가적인 로컬 feature $\mathbf{f} \in \mathbb{R}^{24}$만 전달한다.
\[\begin{equation} \Theta (\mathbf{f}) \; \rightarrow \; \{ \lambda, \mu, \xi \}_N \end{equation}\]고주파수 정보와 저주파수 정보를 더 잘 구별하고 ASG가 고주파수 반사 디테일을 피팅하는 데 도움을 주기 위해 색상 $c$를 diffuse 성분과 specular 성분으로 분해한다.
\[\begin{equation} c = c_d + c_s \end{equation}\]여기서 $c_d$는 SH의 처음 세 차수를 사용하여 모델링된 diffuse color이고, $c_s$는 ASG를 통해 계산된 specular color이다. 외형 모델링에 대한 이러한 포괄적인 접근 방식을 ASG appearance field라고 부른다.
ASG는 이론적으로 비등방성을 모델링하는 SH의 능력을 향상시키지만 ASG를 직접 사용하여 각 3D Gaussian의 specular color를 정확하게 모델링하는 데 여전히 부족하다. 따라서 색상을 직접 표현하는 데 ASG를 사용하는 대신 ASG를 사용하여 각 3D Gaussian의 latent feature를 모델링한다. 비등방성 정보를 포함하는 이 latent feature는 최종 specular color를 결정하기 위해 feature decoupling MLP $\Psi$에 공급된다.
\[\begin{aligned} & \Psi (\kappa, \gamma (\mathbf{d}), \langle n, -\mathbf{d} \rangle) \; \rightarrow \; c_s \\ & \kappa = \bigoplus_{i=1}^N \textrm{ASG} (\omega_r \; \vert \; [\mathbf{x}, \mathbf{y}, \mathbf{z}], [\lambda_i, \mu_i], \xi_i) \end{aligned}\]여기서 $\kappa$는 ASG에서 파생된 latent feature, $\oplus$는 concatenation 연산, $\gamma$는 위치 인코딩, $\mathbf{d}$는 카메라에서 각 3D Gaussian을 가리키는 단위 뷰 방향, $n$은 각 3D Gaussian의 normal, $\omega_r$은 단위 반사 방향이다. 이 전략은 복잡한 광학 현상이 있는 장면을 모델링하는 3D-GS의 능력을 크게 향상시키며, 일반적인 ASG나 MLP는 이 접근 방식만큼 효과적으로 비등방성 외형 모델링을 할 수 없다.
Normal Estimation
3D-GS는 연속적인 표면을 형성하지 않고 특정 범위 내의 로컬한 공간을 나타내는 개별 엔터티의 컬렉션으로 구성되므로 3D Gaussian의 normal을 직접 추정하는 것은 어려운 일이다. Normal을 계산하려면 일반적으로 연속적인 표면이 필요하며 3D-GS의 각 엔터티의 비등방성 외형은 normal 결정을 더욱 복잡하게 만든다. GaussianShader를 따라 각 Gaussian의 가장 짧은 축을 normal로 사용한다. 이 접근 방식은 3D Gaussian이 최적화 프로세스 중에 점진적으로 평탄화되는 경향이 있어 가장 짧은 축이 normal에 대한 합리적인 근사치 역할을 할 수 있다는 관찰을 기반으로 한다.
반사 방향 $\omega_r$은 뷰 방향과 로컬 normal 벡터 $n$을 사용하여 다음과 같이 구할 수 있다.
\[\begin{equation} \omega_r = 2 (\omega_o \cdot n) \cdot n - \omega_o \end{equation}\]여기서 $\omega_o = -\mathbf{d}$는 world space의 각 3D Gaussian에서 카메라를 가리키는 단위 뷰 방향이다. 반사 방향 $\omega_r$을 사용하여 ASG를 쿼리함으로써 비등방성 정보가 포함된 latent feature를 더 효과적으로 보간할 수 있다. 실험 결과에 따르면 이러한 normal 추정은 실제 세계와 일치하는 물리적으로 정확한 normal을 생성할 수 없지만 ASG가 고주파수 정보를 피팅하는 데 도움이 되도록 상대적으로 정확한 반사 방향을 생성하는 것만으로도 충분하다.
3. Anchor-Based Gaussian Splatting
Neural Gaussian Derivation with ASG Appearance Field
ASG appearance field는 반사 및 비등방성 feature들을 모델링하는 3D-GS의 능력을 크게 향상시키지만, 각 Gaussian과 관련된 추가 로컬 feature로 인해 SH를 사용하는 것에 비해 추가 저장 및 계산 오버헤드가 발생한다. 경계가 있는 장면에서는 100FPS 이상의 실시간 렌더링이 여전히 가능하지만, 실제 경계가 없는 장면에서 ASG로 인해 저장공간 오버헤드가 크게 증가하고 렌더링 속도가 감소하는 것은 용납할 수 없다. 저자들은 Scaffold-GS에서 영감을 받아 앵커 기반 Gaussian splatting을 사용하여 저장공간 오버헤드와 렌더링에 필요한 3D Gaussian 수를 줄여 렌더링 속도를 높였다.
각 앵커 Gaussian은 위치 좌표 \(\mathbf{P}_v \in \mathbb{R}^3\), 로컬 feature \(\mathbf{f}_v \in \mathbb{R}^{32}\), displacement factor $\eta_v \in \mathbb{R}^3$과 k개의 학습 가능한 offset \(\mathbf{O}_v \in \mathbb{R}^{k \times 3}\)을 전달한다. COLMAP에서 얻은 sparse한 포인트 클라우드를 사용하여 각 앵커 3D Gaussian을 초기화하고 neural Gaussian 생성을 가이드하는 복셀 중심 역할을 하도록 한다. 앵커 Gaussian의 위치 \(\mathbf{P}_v\)는 다음과 같이 초기화된다.
\[\begin{equation} \mathbf{P}_v = \bigg\{ \bigg\lfloor \frac{\mathbf{P}}{\epsilon} + 0.5 \bigg\rfloor \bigg\} \cdot \epsilon \end{equation}\]여기서 $\mathbf{P}$는 포인트 클라우드의 위치, $\epsilon$은 복셀 크기, \(\{\cdot\}\)는 중복된 앵커를 제거하는 연산이다.
그런 다음 앵커 Gaussian을 사용하여 3D-GS와 동일한 속성을 갖는 neural Gaussian 생성을 가이드한다. View frustum 내에 보이는 각 앵커 Gaussian에 대해 $k$개의 neural Gaussian을 생성하고 해당 속성을 예측한다. Neural Gaussian의 위치 $\mathbf{x}$는 다음과 같다.
\[\begin{equation} \{\mathbf{x}_0, \ldots, \mathbf{x}_{k-1}\} = \mathbf{P}_v + \{\mathbf{O}_0, \ldots, \mathbf{O}_{k-1}\} \cdot \eta_v \end{equation}\]불투명도 $\sigma$는 작은 MLP를 통해 계산된다.
\[\begin{equation} \{\sigma_0, \ldots, \sigma_{k-1}\} = \mathcal{F}_\sigma (\mathbf{f}_v, \delta_{cv}, \mathbf{d}_{cv}) \end{equation}\]여기서 \(\delta_{cv}\)는 앵커 Gaussian과 카메라 사이의 거리를 나타내고, \(\mathbf{d}_{cv}\)는 카메라에서 앵커 Gaussian을 가리키는 단위 방향을 나타낸다. 각 neural Gaussian의 rotation $r$과 scaling $s$는 각각 작은 MLP \(\mathcal{F}_r\)과 \(\mathcal{F}_s\)를 사용하여 유사하게 얻는다.
ASG로 모델링한 비등방성은 공간에서 연속적이므로 저차원 공간으로 압축할 수 있다. 앵커 Gaussian 덕분에 앵커 feature \(\mathbf{f}_v\)를 직접 사용하여 $N$개의 ASG를 압축하여 저장공간의 압력을 더욱 줄일 수 있다. Neural Gaussian의 위치를 인식하는 ASG를 만들기 위해 단위 뷰 방향을 도입한다. 결과적으로 ASG 파라미터 예측은 다음과 같이 수정된다.
\[\begin{equation} \Theta (\mathbf{f}_v, \mathbf{d}_{cn}) \; \rightarrow \; \{\lambda, \mu, \xi\}_N \end{equation}\]여기서 \(\mathbf{d}_{cn}\)은 카메라에서 각 neural Gaussian까지의 단위 뷰 방향을 나타낸다. 추가적으로 diffuse 성분의 smoothness를 보장하고 수렴의 어려움을 줄이기 위해 MLP $\Psi$를 통해 직접 예측된 neural Gaussian의 diffuse 부분을 \(c_d = \phi (\mathbf{f}_v)\)으로 설정한다.
Adaptive Control of Anchor Gaussians
3D-GS가 중복된 엔터티를 제거하면서 장면 디테일을 표현할 수 있도록 neural Gaussian의 기울기와 불투명도를 기반으로 앵커 Gaussian 수를 적응적으로 조정한다. Scaffold-GS를 따라 각 앵커 Gaussian에 대해 100 iteration마다 생성된 $k$개의 neural Gaussian의 평균 기울기 \(\nabla_v\)를 계산한다. \(\nabla_v > \tau_g\)인 앵커 Gaussian은 densify된다. Scaffold-GS를 따라 공간을 다중 해상도 복셀로 quantize하여 새로운 앵커 Gaussian을 다양한 세분성으로 추가할 수 있도록 한다.
\[\begin{equation} \epsilon^{(l)} = \epsilon \cdot \beta / 4^l, \quad \tau_g^{(l)} = \tau_g \cdot 2^l \end{equation}\]여기서 $l$은 새로운 앵커 Gaussian의 수준을 나타내고, $\epsilon^{(l)}$은 새로 성장한 앵커 Gaussian의 $l$번째 수준에서의 복셀 크기, $\beta$는 성장 factor이다. 저자들은 Scaffold-GS와 달리 앵커의 과도한 densification으로 인한 overfitting을 줄이기 위해 계층적 선택을 도입했다. \(\nabla_v > \textrm{Quantile} (\nabla_v, 2^{-(l+1)})\)인 앵커 Gaussian만 $l$번째 레벨의 해당 복셀 중심에서 densify된다.
불필요한 앵커를 제거하기 위해 100 iteration마다 연관된 neural Gaussian의 불투명도 값을 누적한다 ($\bar{\sigma}$). 앵커 Gaussian이 만족스러운 수준의 불투명도를 갖는 neural Gaussian을 생성하지 못하면 ($\bar{\sigma} < \tau_o$) 앵커를 제거한다.
4. Coarse-to-fine Training

많은 실제 시나리오에서 3D-GS가 학습 데이터에 overfitting되는 경향이 있어 새로운 시점에서 이미지를 렌더링할 때 수많은 floater가 출현한다. 실제 데이터셋의 일반적인 문제는 카메라 포즈 추정의 부정확성이며, 특히 대규모 장면에서 두드러진다. Scaffold-GS는 3D-GS를 고정하여 형상에 sparse한 복셀 제약 조건을 적용하여 계층적 3D-GS 표현을 생성한다. 이러한 계층적 접근 방식은 복잡한 형상을 모델링하는 3D-GS의 능력을 향상시키지만 overfitting 문제를 해결하지 못하고 많은 경우 장면 배경의 floater 존재를 악화시킨다.
실제 장면에서 floater의 발생을 완화하기 위해 coarse-to-fine 학습 메커니즘을 사용한다. 저자들은 3D-GS가 overfitting되는 경향은 더 넓은 글로벌한 정보를 고려하기보다는 특정 픽셀과 이웃에 대한 각 3D Gaussian의 기여도에 지나치게 집중하기 때문에 발생한다고 믿는다. 따라서 3D-GS를 저해상도에서 고해상도로 점진적으로 학습시킨다.
\[\begin{equation} r(i) = \min(\lfloor r_s + (r_e - r_s) \cdot i / \tau \rceil, r_e) \end{equation}\]여기서 $r(i)$는 $i$번째 학습 iteration에서의 이미지 해상도, $r_s$는 시작 이미지 해상도, $r_e$는 종료 이미지 해상도(렌더링하려는 전체 해상도), $\tau$는 경험적으로 20,000으로 설정된 threshold iteration이다.
이러한 접근 방식을 통해 3D-GS는 학습 초기 단계에서 이미지로부터 글로벌 정보를 학습할 수 있으므로 학습 이미지의 로컬 영역에 대한 overfitting을 줄이고 새로운 뷰 렌더링에서 상당한 수의 floater를 제거할 수 있다. 또한 초기 단계의 낮은 해상도 학습으로 인해 이 메커니즘은 학습 시간을 약 20% 단축시킨다.
5. Losses
3D-GS의 color loss 외에도 정규화 loss를 통합하여 neural Gaussian이 작게 유지되고 최소한으로 겹치도록 장려한다. 결과적으로 모든 학습 가능한 파라미터와 MLP에 대한 총 loss function은 다음과 같다.
\[\begin{equation} \mathcal{L} = (1 - \lambda_\textrm{D-SSIM}) \mathcal{L}_1 + \lambda_\textrm{D-SSIM} \mathcal{L}_\textrm{D-SSIM} + \lambda_\textrm{reg} \mathcal{L}_\textrm{reg} \\ \mathcal{L}_\textrm{reg} = \frac{1}{N_n} \sum_{i=1}^{N_n} \textrm{Prod} (s_i) \end{equation}\]여기서 $N_n$은 Gaussian의 수이고 $\textrm{Prod}(\cdot)$는 각 neural Gaussian의 scale $s_i$의 곱을 계산한다. \(\lambda_\textrm{D-SSIM} = 0.2\)이고 \(\lambda_\textrm{reg} = 0.01\)이다.
Experiments
- 구현 디테일
- feature decoupling MLP $\Psi$: 3 layer, 64 hidden unit, 위치 인코딩 차수 = 2
- densification threshold $\tau_g = 0.0002$
- pruning threshold $\tau_o = 0.005$
- 각 앵커의 neural Gaussian의 수 $k = 10$
- 경계가 있는 장면의 경우 voxel size $\epsilon = 0.001$, growth factor $\beta = 4$
- Mip-NeRF 360 장면의 경우 voxel size $\epsilon = 0.001$, growth factor $\beta = 16$
- 시작 해상도 $r_s$는 원본 이미지를 8배 다운샘플링한 해상도
- 불투명도가 0보다 큰 neural Gaussian만 ASG appearance field와 rasterization 파이프라인을 통과시킴
- GPU: Tesla V100 (FPS는 NVIDIA RTX 3090에서 측정)
1. Results and Comparisons
Synthetic Bounded Scenes
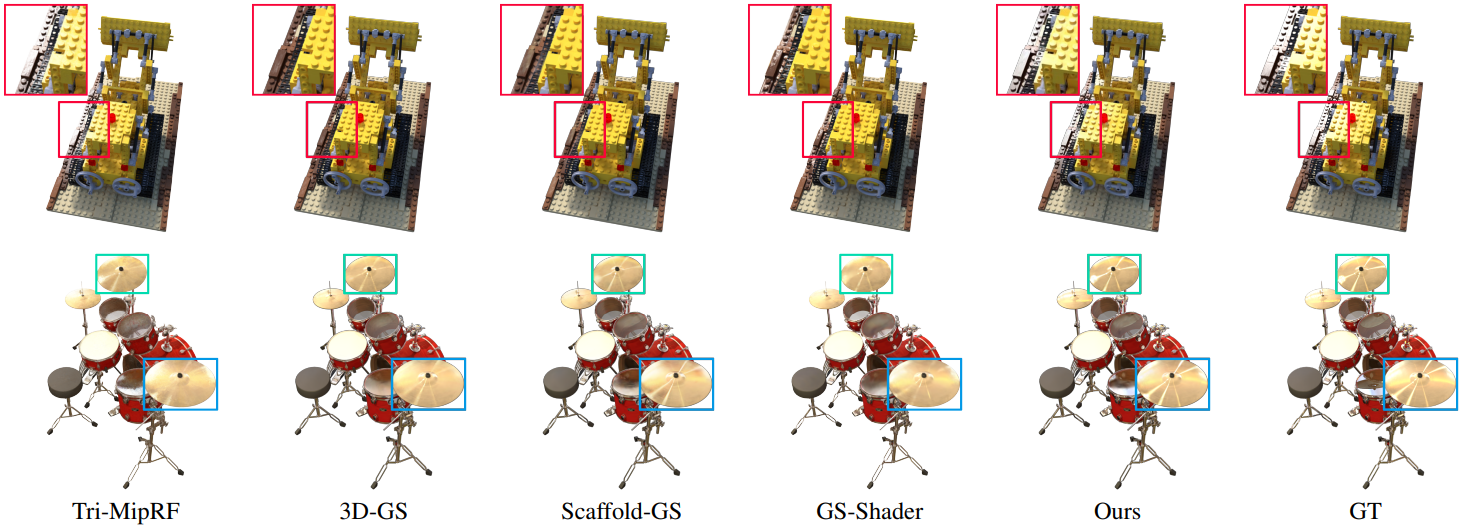
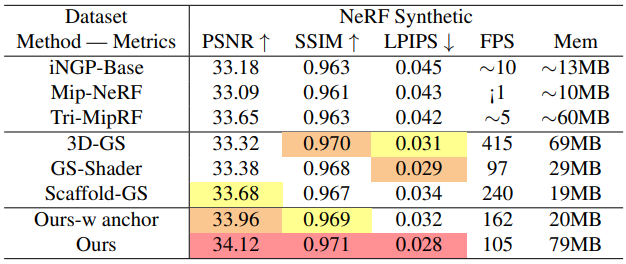
다음은 NeRF 데이터셋에 대한 결과를 비교한 것이다.
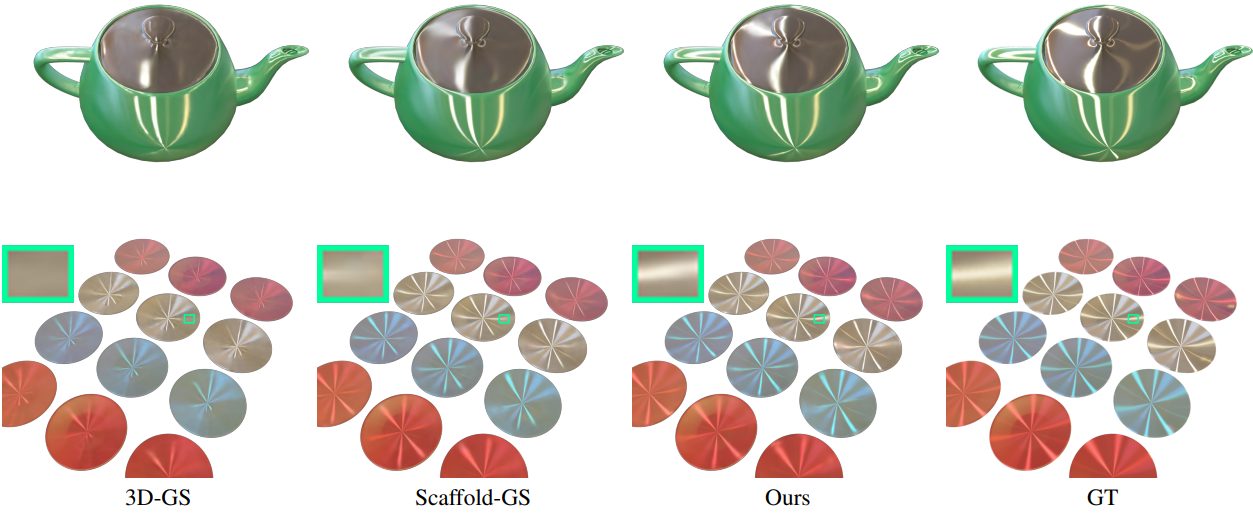
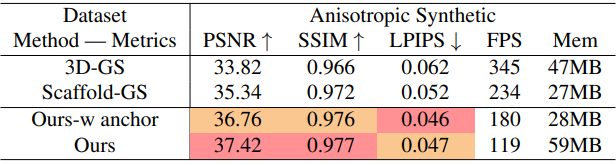
다음은 anisotropic 데이터셋에 대한 결과를 비교한 것이다.
다음은 NSVF 데이터셋에 대한 결과를 비교한 것이다.


Real-world Unbounded Scenes
다음은 현실 데이터셋에 대한 결과를 비교한 표이다.

다음은 Mip-NeRF 360 데이터셋에 대한 결과를 비교한 것이다.

2. Ablation Study
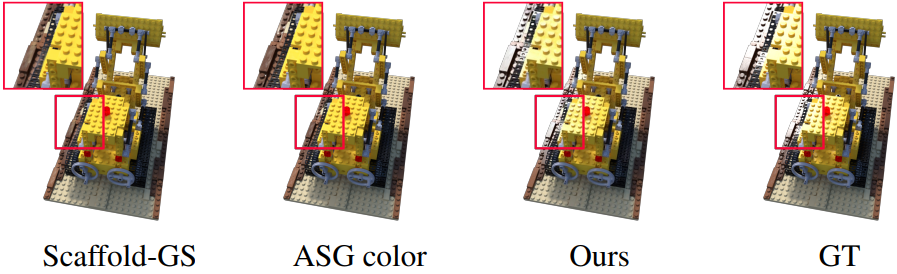
다음은 ASG feature decoupling MLP에 대한 ablation 결과이다.
다음은 coarse-to-fine 학습 메커니즘에 대한 ablation 결과이다.
