[논문리뷰] SparseGS: Real-Time 360° Sparse View Synthesis using Gaussian Splatting
3DV 2025. [Paper] [Page]
Haolin Xiong, Sairisheek Muttukuru, Rishi Upadhyay, Pradyumna Chari, Achuta Kadambi
University of California, Los Angeles
30 Nov 2023

Introduction
3D Gaussian Splatting은 NeRF의 아이디어를 기반으로 구축되었지만 NeRF의 암시적 신경망을 3D Gaussian을 기반으로 한 명시적 표현으로 대체하였다. 이러한 Gaussian은 포인트 기반 splatting을 사용하여 렌더링된다. 이를 통해 렌더링 속도는 빨라지지만 세밀한 하이퍼파라미터 튜닝이 필요하다. NeRF와 3D Gaussian Splatting은 모두 ovel view synthesis를 잘 수행하지만, 다양한 조명 조건, 날씨에 따른 제약 등과 같은 이유로 인해 대규모 학습 뷰 세트가 필요한 경향이 있다. 이에 따라 few-shot novel view synthesis 기법에 대한 관심이 높아지고 있다.
Few-shot 뷰 합성 문제는 2D 이미지에서 3D 구조를 학습할 때 내재된 모호성이 크게 악화되기 때문에 특히 어렵다. 뷰 수가 적으면 장면의 많은 영역이 거의 또는 전혀 적용되지 않는다. 따라서 2D 학습 뷰를 올바르게 표현할 수 있는 잘못된 3D 표현이 많이 있을 수 있지만 floater나 background collapse와 같은 아티팩트로 인해 새로운 뷰를 렌더링할 때 결과가 좋지 않을 수 있다. 이전 연구들에서는 뷰 또는 렌더링된 깊이 맵 간의 변화를 정규화하는 제약 조건을 도입하여 이 문제를 해결했다. 이 분야의 가장 최근의 이전 연구는 NeRF를 기반으로 구축되었으므로 결과적으로 긴 학습 시간과 신경망의 고유한 블랙박스 특성으로 인해 제한된다. 투명성이 부족하면 당면한 문제에 대한 직접적인 접근을 방해하는 상당한 제약이 발생한다. 대신, 세심하게 설계된 loss function과 제약 조건을 사용하여 이러한 문제에 간접적으로 접근한다.
본 연구에서는 3D Gaussian Splatting 위에 구축된 few-shot novel view synthesis 기술을 구축하였다. 기본 표현의 명시적 특성을 통해 direct floater pruning이라는 새로운 핵심 연산을 도입할 수 있다. 이 연산을 통해 렌더링된 이미지에서 floater나 background collapse로 인해 문제가 있는 부분을 식별하고 3D 표현을 직접 편집하여 이러한 아티팩트를 제거할 수 있다. 결과적으로 이 연산이 적용되는 시기와 학습 중 장면 표현을 기반으로 이 연산이 얼마나 선택적으로 적용되는지에 대해 더 큰 제어권을 갖게 된다. 또한 저자들은 이 새로운 연산자 외에도 이미지 생성 diffusion model의 최근 발전을 활용하여 학습 뷰에서 커버리지가 거의 없는 영역에 supervision을 제공하고 깊이 제약 조건을 적용하였다.
Methods
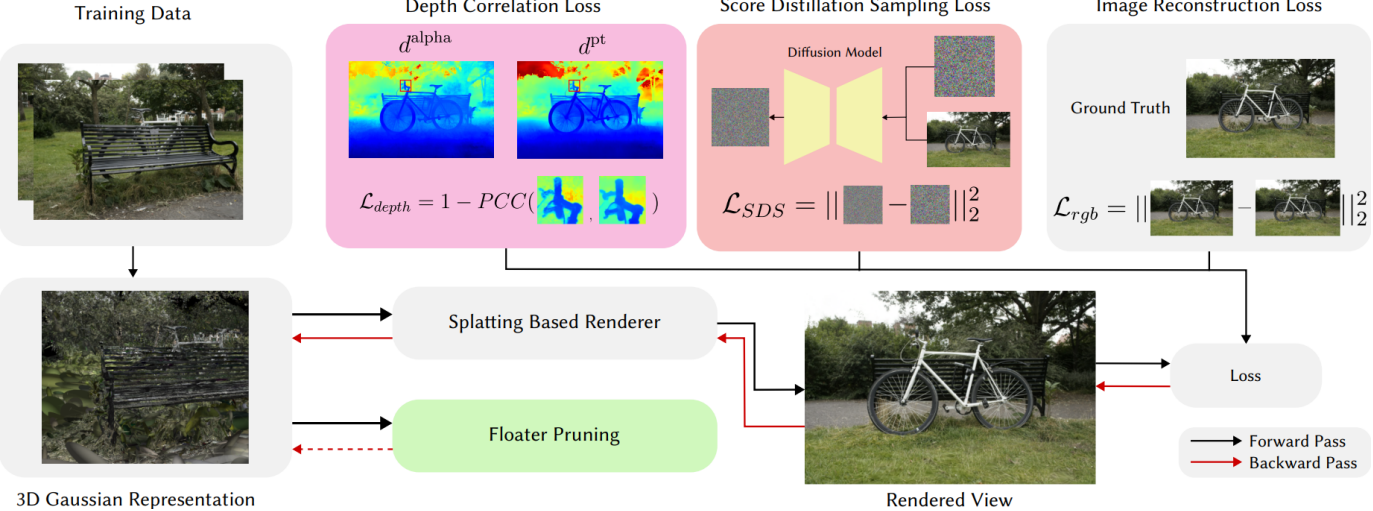
본 논문의 방법은 새로운 뷰에 대한 뷰 일관성과 깊이 정확도를 향상시키기 위해 설계된 세 가지 주요 구성 요소로 구성된다.
- depth correlation loss
- diffusion loss
- floater pruning operation
Rendering Depth from 3D Gaussians
저자들이 도입한 많은 구성 요소는 3D Gaussian 표현에서 렌더링된 깊이 맵에 의존한다. 이를 계산하기 위해 alpha-blending과 mode-selection이라는 두 가지 기술을 사용한다. Alpha-blending은 컬러 이미지 렌더링에 사용된 것과 동일한 절차에 따라 깊이 맵을 렌더링한다. 픽셀 $x, y$에서의 alpha-blended depth $d_{x,y}^\textrm{alpha}$는 다음과 같이 계산할 수 있다.
\[\begin{equation} d_{x,y}^\textrm{alpha} = \sum_i^N T_i \alpha_i d_i \end{equation}\]여기서 $T_i$는 누적 투과율이고 $\alpha_i$는 알파 합성 가중치이다. Mode-selection에서 $w_i = T_i \alpha_i$가 가장 큰 기여를 하는 Gaussian의 깊이는 해당 픽셀의 깊이를 나타낸다. Mode-selected depth는 다음과 같이 쓸 수 있다.
\[\begin{equation} d_{x,y}^\textrm{mode} = d_{\arg \max_i (w_i)} \end{equation}\]직관적으로 mode-selected depth는 불투명도가 높은 첫 번째 Gaussian을 선택하는 것으로 생각할 수 있는 반면, alpha-blended depth는 카메라의 가상 광선을 따라 거의 모든 Gaussian을 고려한다. 나중에 pruning 연산자를 구축하기 위해 의존하게 될 주요 통찰력은 $d^\textrm{mode}$와 $d^\textrm{alpha}$가 가장 이상적인 설정에 있어야 함에도 불구하고 항상 동일하지는 않다는 것이다. 이에 대한 그림이 아래에 나와 있다.
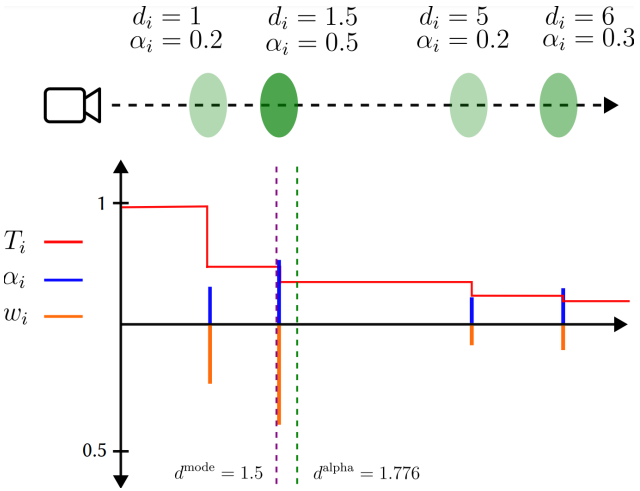
여기에는 광선을 따라 다양한 깊이와 다양한 불투명도를 갖는 4개의 Gaussian이 있다. 처음에 $T$는 1에서 시작한다. 참고로 $w_i = T_i \alpha_i$, $T_i = T_{i−1} (1 − \alpha_{i−1})$, $T_0 = 1$이다. $w_i$의 최대값은 두 번째 Gaussian에서 $w_i = 0.4$이므로 $d^\textrm{mode} = 1.5$이다. 그러나 모든 $w_i$ 값을 계산하고 깊이의 가중 합을 취하면 $d^\textrm{alpha} = 1.776$이다.
Alpha-blended depth는 불투명도가 낮은 Gaussian이 양쪽으로 끌어당기기 때문에 mode-select된 깊이보다 약간 뒤에 있다. 이로 인해 실제 깊이가 무엇인지 모호해진다. 저자들은 이 모호함을 한 포인트에서 3DGS의 불확실성을 측정하는 것으로 해석하고 이를 나중에 소개할 pruning 연산자에게 알리는 데 사용한다.
저자들은 추가로 사전 학습된 깊이 추정 모델로 학습 뷰에서 psuedo-ground truth depth map $d^\textrm{pt}$를 계산하였다. 저자들은 Monodepth를 사용하였지만 어떠한 사전 학습된 깊이 추정 모델도 사용할 수 있다.
Patch-based Depth Correlation Loss
Alpha-blended depth와 mode-selected depth는 COLMAP에 기반하지만 깊이 추정 모델은 상대적인 깊이를 예측하므로 평균 제곱 오차(MSE)와 같은 loss를 직접 적용하는 것은 잘 작동하지 않는다. 한 가지 옵션은 scale과 shift 파라미터를 추정하고 이를 사용하여 메트릭 공간에서 두 깊이 맵을 정렬하는 것이다. 그러나 깊이 맵 간의 변환은 모든 포인트에서 일정하다고 보장되지 않는다. 즉, naive한 정렬로 인해 원치 않는 추가 왜곡이 발생할 수 있다.
대신, 저자들은 이미지 패치 전반에 걸쳐 Pearson correlation을 활용하여 깊이 맵 간의 유사한 메트릭을 계산할 것을 제안하였다. 이는 이전 연구들에서 제안된 depth ranking loss들과 유사하지만 iteration마다 선택된 두 포인트를 비교하는 대신 전체 패치를 비교한다. 즉, 이미지의 더 큰 부분에 한 번에 영향을 미칠 수 있고 더 많은 로컬 구조를 학습할 수 있다. Pearson correlation은 정규화된 cross correlation과 동일하므로 두 깊이 맵의 동일한 위치에 있는 패치가 깊이 값의 범위에 관계없이 높은 cross correlation 값을 갖도록 유도된다.
각 iteration에서 $N$개의 겹치지 않는 패치를 무작위로 샘플링하여 depth correlation loss를 다음과 같이 계산한다.
\[\begin{equation} \mathcal{L}_\textrm{depth} = \frac{1}{N} \sum_i^N 1 - \textrm{PCC} (p_i^\textrm{alpha}, p_i^\textrm{pt}) \\ \textrm{PCC} (X, Y) = \frac{\mathbb{E}[XY] - \mathbb{E}[X] \mathbb{E}[Y]}{\sqrt{\mathbb{E}[Y^2]-\mathbb{E}[Y]^2}\sqrt{\mathbb{E}[X^2] - \mathbb{E}[X]^2}} \end{equation}\]여기서 $p_i^\textrm{alpha} \in \mathbb{R}^{S^2}$는 $d^\textrm{alpha}$의 $i$번째 패치이고 $p_i^\textrm{pt} \in \mathbb{R}^{S^2}$는 $d^\textrm{pt}$의 $i$번째 패치이며 패치 크기 $S$는 hyperparameter이다. 직관적으로 이 loss는 일관되지 않은 scale 및 shift 문제를 피하면서 Gaussian 표현의 alpha-blending 깊이 맵을 Monodepth의 깊이 맵과 정렬한다.
Score Distillation Sampling Loss
Few-shot 설정에서는 입력 학습 데이터가 sparse하므로 장면을 완전히 다루지 못할 가능성이 높다. 따라서 저자들은 이미지 생성 모델의 최근 발전에 영감을 받아 사전 학습된 생성 diffusion model을 사용하여 Dreamfusion에서 소개된 Score Distillation Sampling (SDS)를 통해 3D Gaussian 표현을 가이드할 것을 제안하였다. 이를 통해 학습 뷰에서 제대로 적용되지 않은 지역에 대한 그럴듯한 세부 정보를 “환각(hallucinate)”하고 보다 완전한 3D 표현을 생성할 수 있다. 구현은 camera-to-world 좌표계 내에서 새로운 카메라 포즈를 생성하는 것으로 시작된다. 구체적으로, 각 카메라의 up-vector는 다음과 같이 추출된다.
\[\begin{equation} Y = \begin{bmatrix} R_{11} \\ R_{21} \\ R_{31} \end{bmatrix} \end{equation}\]여기서 $R$은 회전 행렬을 나타낸다. 그런 다음 모든 카메라에 걸쳐 정규화된 평균 up-vector를 계산하여 장면 중심의 추정값으로 사용한다. 그런 다음 Rodrigues’ rotation formula를 사용하여 이 추정된 중심 축을 중심으로 현재 뷰의 카메라 중심을 다양한 각도로 회전하여 새로운 뷰를 만든다.
\[\begin{equation} \bar{Y} = \frac{1}{N} \sum_i Y_i \\ \bar{Y} = \frac{\bar{Y}}{\| \bar{Y} \|} \\ P^\prime = P \cos \theta + (P \times \bar{Y}) \sin \theta + \bar{Y} (\bar{Y} \cdot P) (1 - \cos \theta) \end{equation}\]여기서 $P$는 원래 카메라 포즈이고 $\bar{Y}$는 장면 중심에서 추정된 up-axis이다. $\theta$는 미리 설정된 간격 중에서 무작위로 선택된다. 이어서, 새로운 포즈의 렌더링된 이미지에 랜덤 noise가 추가하고 diffusion model을 사용하여 원본 이미지를 예측한다. Diffusion model은 대규모 데이터셋에 대해 학습되고 일반적인 이미지 prior들을 포함하므로 누락된 디테일을 그럴듯한 픽셀 값으로 보간할 수 있다. 실제로 모델에게 이미지 자체보다는 이미지에 추가된 noise를 예측하도록 요청하고, 추가된 noise와 예측된 noise 간의 차이는 3D Gaussian 표현을 위한 guidance 역할을 한다. Guidance loss는 다음과 같다.
\[\begin{equation} \hat{I} = \mathcal{N} (\sqrt{\hat{\alpha}} I^\prime, (1 - \hat{\alpha}) \mathbf{I}) \\ \mathcal{L}_\textrm{SDS} = \nabla_G \mathbb{E} [(\epsilon_\phi (\hat{I}_p; \tilde{I}_p) - \epsilon) \frac{\partial \hat{I}_p}{\partial G}] \end{equation}\]여기서 $G$는 Gaussian 표현의 파라미터, $\hat{\alpha}$는 1에서 분산 schedule을 뺀 누적 곱, $\epsilon$은 SDS에 의해 추가된 noise, $\epsilon_\phi(\cdot)$는 Stable Diffusion에 의해 예측된 noise, \(\hat{I}_p\)는 카메라에 렌더링된 이미지, $p$는 noise가 추가된 포즈, \(\tilde{I}_p\)는 Stable Diffusion에 의해 noise가 제거된 이미지이다.
직관적으로 SDS loss는 먼저 이미지에 추가된 실제 noise와 diffusion model이 추정하는 noise 사이의 오차를 찾은 다음 Gaussian 모델의 파라미터(ex. mean, scaling, rotation, opacity)와 관련하여 이 오차의 기울기를 취한다.
Floater Removal
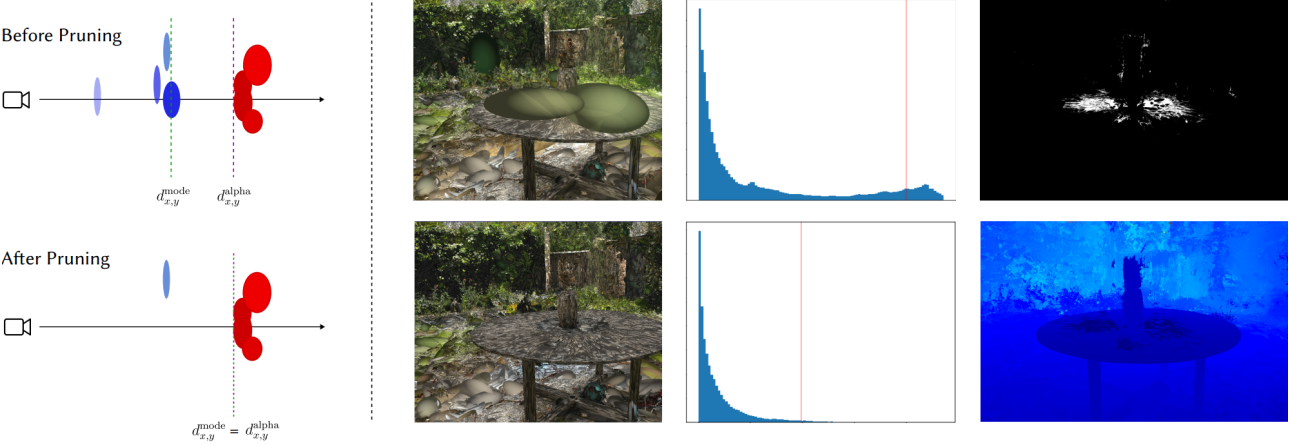
모델이 depth correlation loss로 학습되었지만 alpha-blended depth만 최적화하는 것만으로는 floater 문제를 해결할 수 없다. Floater를 제거하기 위해 저자들은 3D Gaussian의 명시적인 표현을 활용하여 floater를 제거하고 모델이 학습 뷰의 해당 영역을 올바르게 다시 학습하도록 장려하는 새로운 연산자를 제안하였다. Floater는 종종 카메라 평면 가까이에 위치하는 상대적으로 불투명도가 높은 Gaussian으로 나타난다. 결과적으로 장면의 alpha-blended depth를 렌더링할 때 눈에 띄게 나타나지는 않지만 평균화되기 때문에 mode-selected 깊이에서는 눈에 띄게 나타난다. 이 차이를 활용하여 각 학습 뷰에 대한 floater mask $F$를 생성한다. 이미지 공간에서 이 마스크를 식별한 후 mode gaussian까지의 모든 Gaussian을 선택하고 pruning한다.
구체적으로, 단일 학습 뷰 $i$에 대해 다음과 같이 $F$를 계산한다. 먼저 mode-selected depth와 alpha-blended depth 간의 상대적인 차이인 $\Delta_i$를 계산한다. $\Delta_i$의 분포를 시각화할 때, 저자들은 floater가 많은 이미지가 bi-modal histogram을 가지고 있음을 발견했다. Floater는 실제 깊이에서 멀리 떨어져 있는 경향이 있는 반면, floater가 없는 이미지는 더 uni-modal인 경향이 있기 때문이다. 이를 활용하여 분포에 대해 uni-modality의 척도인 dip test를 수행한다. 그런 다음 floater 수는 일반적으로 장면 전반에 걸친 메트릭이므로 장면의 모든 학습 뷰에서 uni-modality 점수의 평균을 구하고 평균을 사용하여 상대적인 차이에 대한 cut-off threshold를 선택한다. Dip 통계에서 threshold으로의 변환 프로세스는 파라미터 $a$, $b$가 있는 지수 곡선을 사용하여 수행된다. 저자들은 다양한 데이터셋과 실제 캡처의 다양한 장면에 대해 $\Delta_i$와 $F_i$를 수동으로 검사하여 이러한 파라미터를 추정하였다. 이 프로세스는 floater pruning이 적응 가능하도록 세심하게 설계되었다. 어떤 경우에는 3D 장면의 품질이 이미 꽤 높아서 floater가 많지 않은 경우도 있다. 이러한 상황에서 정리할 픽셀 비율에 대해 미리 정의된 임계값을 설정하면 장면에서 디테일을 강제로 삭제하게 된다. 마찬가지로 일부 장면은 3D 구조 또는 학습 이미지의 분포로 인해 학습하기가 특히 어렵다. 이러한 경우 pruning을 통해 평소보다 더 많은 floater를 제거해야 한다. 평균 dip score $\bar{D}$는 장면에 얼마나 많은 floater가 포함되어 있는지에 대한 척도를 제공하고 이에 대응하여 기술을 조정할 수 있도록 해준다. 프로세스는 다음과 같이 쓸 수 있다.
\[\begin{equation} \Delta_i = \frac{d_i^\textrm{mode} - d_i^\textrm{alpha}}{d_i^\textrm{alpha}} \\ \bar{D} = \frac{1}{N} \sum_i D (\Delta_i) \\ \tau = \textrm{percentile} (\Delta_i, ae^{b \bar{D}}) \\ F_i = \unicode{x1D7D9}[\Delta_i > \tau] \end{equation}\]전체 pruning 프로세스는 Algorithm 1과 같다.

Full Loss
모두 결합하면 전체 loss는 다음과 같다.
\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{rgb} (\hat{I}, I) + \lambda_\textrm{depth} \mathcal{L}_\textrm{depth} (d^\textrm{\alpha}, d^\textrm{pt}) + \lambda_\textrm{SDS} \mathcal{L}_\textrm{SDS} (\hat{I}^\prime) \end{equation}\]여기서 $\hat{I}$는 렌더링된 이미지이고, $I$는 실제 이미지이며, \(\hat{I}^\prime\)는 학습 뷰가 아닌 임의의 새로운 뷰에서 렌더링된 이미지이다. \(\mathcal{L}_\textrm{rgb}\)는 3D Gaussian Splatting을 학습시키는 데 사용되는 것과 동일한 loss이다.
Results
- 구현 디테일
- iteration: 30,000
- depth correlation loss: 패치 크기는 128px, 각 iteration에서 전체 패치 중 50%만 사용
- diffusion loss: 마지막 10,000 iteration에 20% 확률로 적용
- floater pruning: 20,000번째 및 25,000번째 iteration에 적용 ($a = 97$, $b = -8$)
- \(\lambda_\textrm{depth} = 0.1\), \(\lambda_\textrm{SDS} = 5 \times 10^{-4}\)
Mip-NeRF 360 Dataset
다음은 Mip-NeRF 360 데이터셋에서 few-shot novel view synthesis에 대해 이전 SOTA들과 비교한 결과이다.

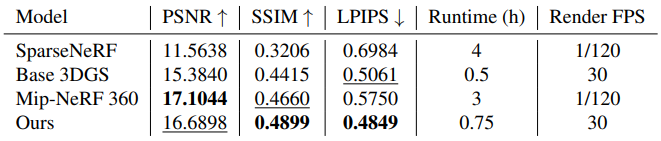
다음은 1/4 해상도에 대한 비교 결과이다.


Ablation Studies
다음은 ablation study 결과이다. (Mip-NeRF 360 - garden)


Limitations
본 논문의 방법은 3D Gaussian Splatting을 기반으로 구축되었기 때문에 COLMAP에서 제공하는 초기 포인트 클라우드에 크게 의존한다. 이 포인트 클라우드가 부정확하거나 디테일이 부족한 경우 모델이 적절하게 보상하는 데 어려움을 겪을 수 있으며 특히 장면 중심에서 멀리 떨어진 영역에서 under-reconstruction으로 이어질 수 있다. 이러한 제한은 초기 학습 뷰의 커버리지가 부족하기 때문에 sparse view 설정에서 특히 두드러진다. 결과적으로 입력 포인트 클라우드는 상대적으로 작으며 테스트된 많은 장면이 총 20개 미만의 포인트로 초기화되었다.