[논문리뷰] SparseFlex: High-Resolution and Arbitrary-Topology 3D Shape Modeling

ICCV 2025 Oral. [Paper] [Page] [Github]
Xianglong He, Zi-Xin Zou, Chia-Hao Chen, Yuan-Chen Guo, Ding Liang, Chun Yuan, Wanli Ouyang, Yan-Pei Cao, Yangguang Li
Tsinghua University | VAST | The Chinese University of Hong Kong
27 Mar 2025

Introduction

렌더링 기반 학습은 3D 표현 및 3D 생성 모델 학습을 위한 강력하고 미분 가능한 해결책을 제공한다. 생성된 메쉬의 렌더링된 이미지를 실제 데이터와 직접 비교함으로써, 렌더링 loss는 초기의 철저한 전처리 단계가 필요 없게 되고 세부적인 디테일도 더 잘 보존된다. 그러나 dense한 implicit field와 함께 사용할 경우, 렌더링 학습은 고해상도에서 매우 높은 메모리 사용량을 요구하여 달성 가능한 충실도를 심각하게 제한한다.

본 논문에서는 이러한 한계를 해결하고 렌더링 학습을 활용하여 고해상도의 미분 가능한 메쉬 재구성 및 생성을 가능하게 하는 새로운 sparse voxel 구조 isosurface 표현 방식인 SparseFlex를 소개한다. SparseFlex는 Flexicubes를 기반으로 구축되어 정확하고 미분 가능한 isosurface 추출을 제공한다. 핵심 설계는 기존의 dense grid 대신 sparse voxel 구조를 사용하는 것이다. 이러한 sparsity는 두 가지 이유에서 매우 중요하다.

1. 메모리 사용량을 크게 줄여 고해상도 모델링을 가능하게 한다.
2. 열린 경계 근처의 voxel을 효과적으로 잘라내어 열린 표면을 표현할 수 있다.

SparseFlex의 능력을 최대한 활용하기 위해, frustum-aware sectional voxel training을 제안하였다. 이 접근법은 각 학습 iteration에서 카메라의 viewing frustum 내에 있는 SparseFlex voxel의 하위 집합만 활성화한다. 또한, frustum의 파라미터를 제어하는 ​​적응형 전략을 도입하여 메모리 사용량을 더욱 최적화한다. 이를 통해 연산 및 메모리 오버헤드를 크게 줄일 수 있을 뿐만 아니라, 카메라의 적절한 위치 조정을 통해 렌더링 loss만으로 메쉬 내부를 재구성할 수 있게 되었다.

저자들은 SparseFlex와 frustum-aware training을 기반으로 완전한 3D shape 모델링 파이프라인을 제시하였다. TRELLIS에서 영감을 얻었지만 주요 수정 사항이 있는 VAE 아키텍처를 사용한다. 첫째, 고충실도 geometry에 중점을 두기 때문에 VAE에 포인트 클라우드를 입력으로 사용하여 표면을 직접적이고 상세하게 표현한다. 또한, 디코더 내에 self-pruning upsampling 모듈을 도입하여 sparse voxel 구조를 더욱 세분화하는데, 이는 특히 열린 표면을 표현하는 데 유용하다. 그런 다음, 학습된 latent space에서 rectified flow transformer를 학습시켜 고품질의 이미지를 조건으로 3D shape을 생성한다.

본 논문의 방법은 최소한의 디테일 저하로 SOTA 재구성 정확도와 고품질의 단일 이미지 기반 3D shape 생성을 보여주었다.

Method

1. SparseFlex Representation

SparseFlex의 핵심 설계는 sparse voxel 구조를 도입하여 고해상도 형상 표현을 가능하게 하는 동시에 메모리 사용량을 대폭 줄이는 것이다. SparseFlex는 dense grid 대신, 표면 근처에 집중된 훨씬 적은 voxel 집합 $\mathcal{V}$를 사용하여 형상을 표현한다. 이러한 sparsity는 두 가지 이유에서 매우 중요하다.

1. Dense grid보다 훨씬 높은 해상도를 얻을 수 있다.
2. 빈 영역의 voxel을 생략함으로써 열린 표면을 자연스럽게 표현할 수 있다.

구체적으로, SparseFlex는 $N_v$개의 voxel들의 집합 \(\mathcal{V} = \{v_i = (x_i, y_i, z-i)\}\)로 정의되며, $v_i$는 $i$번째 voxel 중심의 3D 좌표를 나타낸다. 각 voxel은 interpolation 가중치

\[\begin{equation} \{\alpha_i \in \mathbb{R}_{>0}^8, \beta_i \in \mathbb{R}_{>0}^{12} \, \vert \, 0 \le i < N_v\} \end{equation}\]

와 연관된다. 이러한 voxel과 연관된 corner grid의 수를 $N_c$라 하면, 각 corner grid는 SDF 값 \(\{s_j \vert 0 \le j < N_c\}\)와 변형 벡터 \(\{\delta_j \vert 0 \le j < N_c\}\)와 연관된다. Sparsity로 인해 $N_v \ll N_r^3$이고 $N_c \ll N_g^3$이며 ($N_r$은 dense voxel의 해상도, $N_g$는 SDF grid의 해상도), Flexicubes 표현과 비교하여 메모리 사용량이 상당히 감소한다. 이러한 sparse voxel에는 Dual Marching Cubes (DMC)만 적용하여 표면을 추출한다. SparseFlex 표현 $\mathcal{S}$는 다음과 같이 정의된다.

\[\begin{equation} \mathcal{S} = (\mathcal{V}, \mathcal{F}_c, \mathcal{F}_v), \quad \mathcal{F}_c = \{s_j, \delta_j\}, \quad \mathcal{F}_v = \{\alpha_i, \beta_i\} \end{equation}\]

($\mathcal{V}$는 voxel 중심, \(\mathcal{F}_c\)는 SDF 값과 corner grid의 변형, \(\mathcal{F}_v\)는 각 voxel의 interpolation 가중치)

SparseFlex는 미분 가능하기 때문에 렌더링 loss를 활용한 end-to-end 최적화가 가능하다. 이를 통해 빈틈없는 메쉬 전처리가 필요 없어 세부적인 디테일을 보존할 수 있다. 또한, SDF의 연속적이고 변형 가능한 특성과 결합된 sparse voxel 구조는 고품질의 열린 표면 메쉬의 정확하고 효율적인 표현을 가능하게 한다. 이러한 sparsity는 효율적인 frustum-aware training의 기반을 마련한다.

2. SparseFlex VAE for Shape Modeling

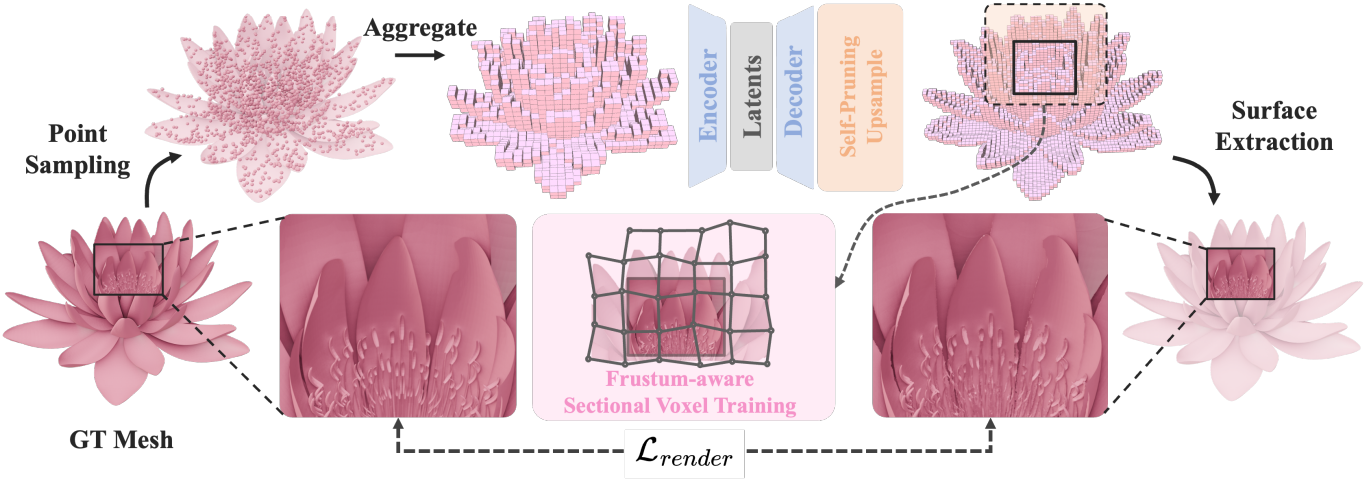
3D shape의 압축적이고 분산된 latent space를 학습시키기 위해, SparseFlex 표현을 활용하는 VAE를 사용한다. VAE는 입력 공간과 저차원 latent space 간의 확률적 매핑을 학습하여 형상의 재구성과 생성을 모두 가능하게 한다. 본 논문의 아키텍처는 TRELLIS에서 영감을 얻었지만, SparseFlex의 장점을 활용하기 위해 주요 부분을 수정했다.

Encoder

인코더에 대한 입력은 3D 메쉬 표면에서 균일하게 샘플링된 포인트 클라우드 \(\mathcal{P} = \{p_i \in \mathbb{R}^3\}_{i=1}^{N_p}\)이며, 해당 normal \(\mathcal{N} = \{n_i \in \mathbb{R}^3\}_{i=1}^{N_p}\)와 함께 제공된다. 먼저 포인트 클라우드를 voxelize하여 SparseFlex 표현 $\mathcal{S}$의 sparse voxel 구조 $\mathcal{V}$를 얻는다.

그런 다음, 얕은 PointNet을 사용하여 각 voxel 내의 로컬한 geometry feature를 집계한다. 구체적으로, 각 voxel $v_i \in \mathcal{V}$에 대해 해당 voxel 내에 포함된 포인트에 로컬 max-pooling 연산을 적용하여 feature 벡터 $f_i$를 생성한다. 이러한 voxel feature \(\mathcal{F} = \{f_i\}\)는 sparse voxel 구조 $\mathcal{V}$와 함께 sparse transformer backbone으로 입력된다. 이 backbone은 TRELLIS와 유사한 shifted window attention을 활용하지만 $\mathcal{F}$와 $\mathcal{V}$에서 직접 작동하도록 조정되었다. Transformer는 인코딩된 3D shape을 나타내는 latent code $z \in \mathbb{R}^{d_z}$를 출력한다.

Decoder

디코더는 latent code $z$를 입력으로 받아 SparseFlex 인스턴스의 파라미터 \(\mathcal{S} = (\mathcal{V}, \mathcal{F}_c, \mathcal{F}_v)\)를 예측한다. 최종 linear layer로 끝나는 일련의 transformer layer를 사용하여 각 corner grid의 SDF 값 $s_j$와 변형 \(\delta_j\)를 예측하고, 각 voxel의 interpolation 가중치 \(\alpha_i\)와 \(\beta_i\)도 예측한다.

Upsampling Modules

저자들은 고해상도 재구성을 달성하기 위해, 디코더 내에 두 개의 convolution 기반의 self-pruning 업샘플링 모듈을 transformer 다음에 통합했다. 이 모듈들은 SparseFlex 표현의 해상도를 점진적으로 높인다. 각 업샘플링 모듈은 기존 voxel을 더 작은 voxel로 세분화하여 해상도를 4배 높이며, 각 모듈은 예측된 occupancy 값을 기반으로 중복 voxel을 제거한다. 세분화 후 voxel에 입력 포인트 클라우드 $\mathcal{P}$의 포인트가 포함되어 있으면 점유된 것으로 간주된다. 이 프로세스는 SparseFlex 표현의 sparsity를 유지하는 데 필수적이며, 빈 영역에서 불필요한 voxel을 제거하므로 열린 표면을 정확하게 표현하는 데 특히 유용하다.

3. Training SparseFlex VAE

렌더링 loss를 활용하여 SparseFlex VAE를 end-to-end로 학습시키고, SparseFlex 표현의 미분 가능성과 frustum-aware sectional voxel training이라는 새로운 학습 전략을 활용한다. 이 전략은 학습 중 메모리 소비를 획기적으로 줄여 기존 방식으로는 불가능했던 고해상도(최대 $1024^3$)를 구현할 수 있게 해준다.

Frustum-aware Sectional Voxel Training

SparseFlex의 sparse voxel 구조에도 불구하고, 고해상도에서 전체 표현을 직접 렌더링하는 것은 계산적으로 비쌀 수 있다. 또한, 표준 렌더링 loss는 일반적으로 보이는 표면에만 초점을 맞추고 형상의 내부는 무시한다. 게다가, 메쉬에서 렌더링 loss에 의존하는 최근 방법들은 일반적으로 전체 메쉬를 추출해야 하는데, 이는 dense한 표현이 부분 추출을 쉽게 허용하지 않기 때문이다. 이와 대조적으로, 본 논문에서 제안하는 sparse 표현은 자연스럽게 부분 추출을 가능하게 한다.

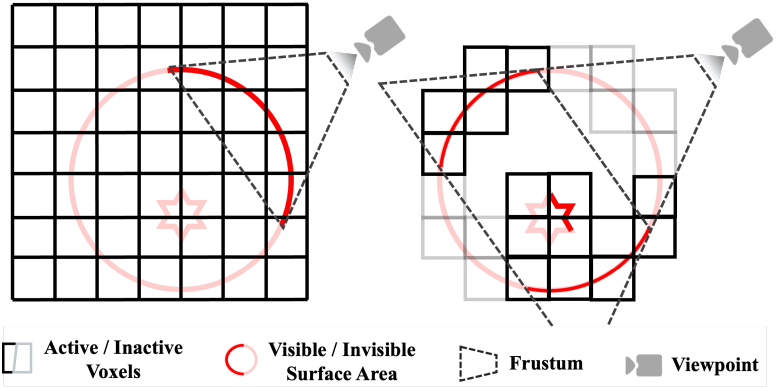
이러한 문제를 해결하기 위해, 본 논문에서는 frustum-aware sectional voxel training을 도입하였다. 구체적으로, 각 학습 iteration 동안 카메라의 viewing frustum 내에 있는 voxel만 활성화한다. Voxel을 활성화한다는 것은 isosurface 추출 및 렌더링 프로세스에 voxel을 포함하는 것을 의미한다. “Sectional”은 한 번에 3D 공간의 일부만 처리하여 메모리 사용량을 크게 줄인다는 것을 의미한다.

카메라의 extrinsic $\pi$, intrinsic $K$, viewing frustum의 clipping 평면 $n$(near)과 $f$(far)가 주어지면, Model-View-Projection (MVP) 행렬 $\textbf{MVP}$를 계산한다. 그런 다음, boolean 연산자를 사용하여 각 voxel $v_i$의 중심이 MVP 행렬로 정의된 viewing frustum 내에 있는지 확인한다. 활성화된 voxel 집합 \(\mathcal{V}_\textrm{active}\)는 다음과 같이 정의된다.

\[\begin{equation} \mathcal{V}_\textrm{active} = \{v_i \vert I (v_i \in \textrm{Frustum} (\textbf{MVP})) = 1, v_i \in \mathcal{V} \} \end{equation}\]

($I(\cdot)$는 indicator function)

Adaptive Frustum and Interior Reconstruction

SparseFlex에서 활성화된 voxel의 비율을 제어하는 visibility ratio $\alpha$ ($0 < \alpha \le 1$)를 도입한다. 약 $\alpha N_v$개의 voxel이 frustum 내에 있도록 clipping 평면 $n$과 $f$를 적응적으로 조정한다. 먼저 $n$과 $f$를 설정하고, 원하는 비율에 도달할 때까지 활성화된 voxel의 개수에 따라 평면을 반복적으로 조정한다.

이 적응형 frustum은 렌더링 loss만으로 메쉬 내부를 재구성하는 새로운 능력을 제공한다. 가상 카메라를 물체 내부에 배치하거나 $n$을 조정하여 메쉬와 교차하도록 하면 내부 구조를 렌더링하고 학습시킬 수 있다. 또한, 카메라를 줌인하면 메쉬 표면을 더욱 세부적으로 렌더링할 수 있어 고해상도 학습에 더욱 적합하다. 이는 내부 디테일을 포착할 수 없는 watertight한 표현에 의존하는 방식에 비해 상당한 이점이다.

Loss Function

다음과 같은 loss function을 사용하여 end-to-end 방식으로 VAE를 학습시킨다.

\[\begin{equation} \mathcal{L} = \lambda_1 \mathcal{L}_\textrm{render} + \lambda_2 \mathcal{L}_\textrm{prune} + \lambda_3 \mathcal{L}_\textrm{KL} + \lambda_4 \mathcal{L}_\textrm{flex} \end{equation}\]

\(\mathcal{L}_\textrm{render}\)는 렌더링 loss이다. 미분 가능한 렌더링에서 일반적으로 사용되는 loss들을 조합하여 사용한다.

\[\begin{equation} \mathcal{L}_\textrm{render} = \lambda_d \mathcal{L}_d + \lambda_n \mathcal{L}_n + \lambda_m \mathcal{L}_m + \lambda_{ss} \mathcal{L}_{ss} + \lambda_\textrm{lp} \mathcal{L}_\textrm{lp} \end{equation}\]

(\(\mathcal{L}_d\), \(\mathcal{L}_n\), \(\mathcal{L}_m\)은 각각 depth map, normal map, mask map에 대한 L1 loss, \(\mathcal{L}_{ss}\)와 \(\mathcal{L}_{lp}\)는 normal map에만 적용한 SSIM loss와 LPIPS loss)

\(\mathcal{L}_\textrm{prune}\)은 binary cross-entroypy (BCE) loss로 구현된 구조에 대한 loss로, sparse voxel의 구성을 학습시킨다.

\[\begin{equation} \mathcal{L}_\textrm{prune} = \textrm{BCE} (V, \hat{V}) \end{equation}\]

($V$는 입력 포인트 클라우드에서 얻은 voxel의 GT occupancy, $\hat{V}$는 예측된 occupancy)

\(\mathcal{L}_\textrm{KL}\)은 학습된 latent 분포와 표준 normal prior 사이의 KL divergence로, latent space를 정규화한다. \(\mathcal{L}_\textrm{flex}\)는 Flexicubes에서 부드러운 SDF 값을 유도하기 위해 사용한 정규화 항이다.

4. Image-to-3D Generation with Rectified Flow

저자들은 학습된 SparseFlex VAE를 기반으로, TRELLIS와 유사하게 고품질의 이미지로 컨디셔닝된 3D 형상 생성을 위한 파이프라인을 개발하였다. 본 접근 방식은 structure flow model과 structured latent flow model의 두 가지 주요 구성 요소로 구성된다.

Structure Flow Model

먼저, 별도의 간단한 3D convolutional structure VAE를 사용하여 3D shape을 나타내는 dense voxel을 저해상도(1/4 스케일) 공간으로 압축한다. 이후, DINOv2를 사용하여 이미지 조건에 대한 feature를 추출하고 cross-attention을 통해 transformer 모델에 주입한다. 이후, 이 저해상도 공간 내에서 rectified flow 모델을 학습시킨다.

Inference 시에는 입력 이미지가 주어지면 학습된 structure flow model은 이에 대응하는 저해상도 3D 공간을 생성하고, 이 공간은 structure VAE에 의해 디코딩되어 생성된 3D shape의 sparse voxel 구조를 생성한다.

Structured Latent Flow Model

제안된 SparseFlex VAE를 기반으로, 3D shape의 포인트 클라우드와 이에 대응하는 voxelize된 sparse voxel 구조가 구조화된 latent space에 인코딩된다. 이후, DINOv2를 통해 얻은 이미지 feature가 cross-attention을 통해 sparse transformer 모델에 주입되고, 이 구조화된 latent space 내에서 rectified flow 모델이 학습된다.

Inference 시에는 입력 이미지가 주어지면, 먼저 structure flow model과 해당 structure VAE를 사용하여 sparse voxel 구조를 생성한다. 그런 다음, sparse voxel 구조와 입력 이미지를 structured latent flow model에 제공하여 해당 latent 표현을 생성한다. 마지막으로, SparseFlex VAE는 이 latent 표현을 디코딩하여 최종 3D shape을 생성한다.

Experiments

• 데이터: Objaverse와 Objaverse-XL을 필터링하여 얻은 약 40만 개의 3D 메쉬
• 구현 디테일
  • SparseFlex VAE는 해상도를 점진적으로 키워가며 학습 (256, 512, 1024)
  • GPU: A100 64개
  • optimizer: AdamW (learning rate = $10^{-4}$, weight decay = 0.01)
  • batch size: VAE 학습 시 64, flow model 학습 시 256
  • inference
    • classifier-free guidance: 3.5
    • 샘플링 step: 50

1. VAE Reconstruction Evaluation

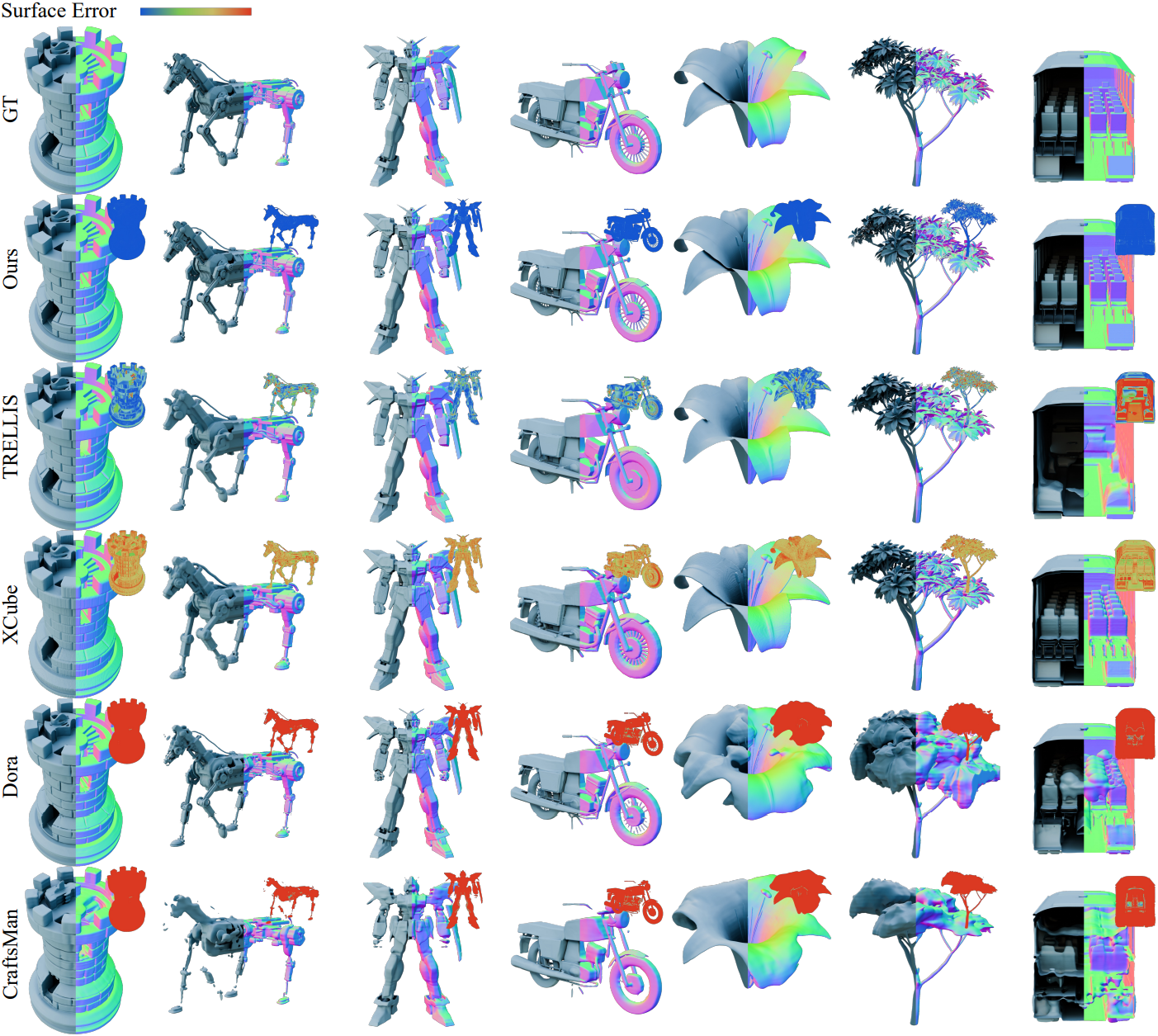
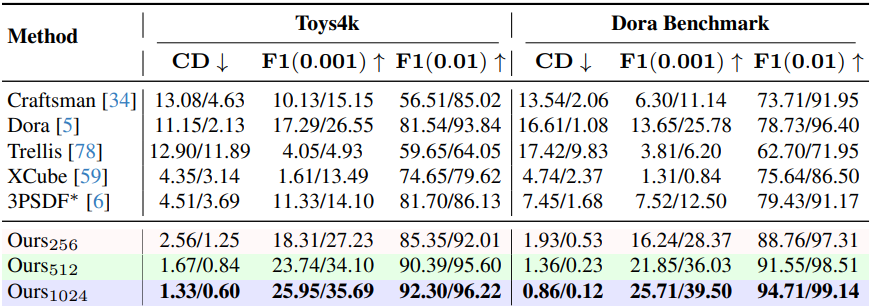
다음은 VAE 재구성 품질을 비교한 결과이다.

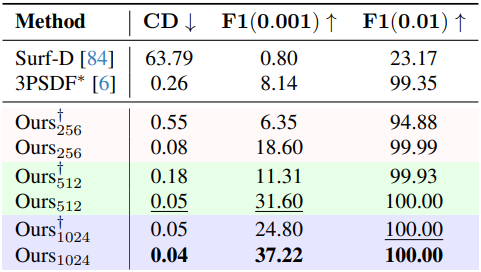
다음은 열린 표면 데이터셋인 Deepfashion3D에서 재구성 품질을 비교한 결과이다. ($\vphantom{1}^\dagger$는 self-pruning 업샘플링 모듈을 사용하지 않은 모델)

2. Image to 3D Genration

다음은 image-to-3D 생성 품질을 비교한 결과이다.

3. Ablation Studies

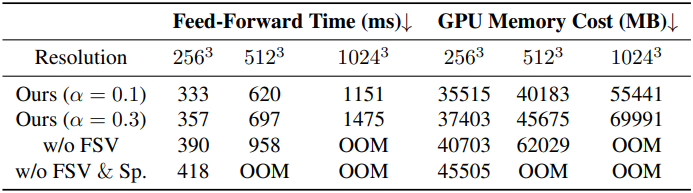
다음은 inference 시간과 GPU 메모리 비용을 비교한 결과이다.

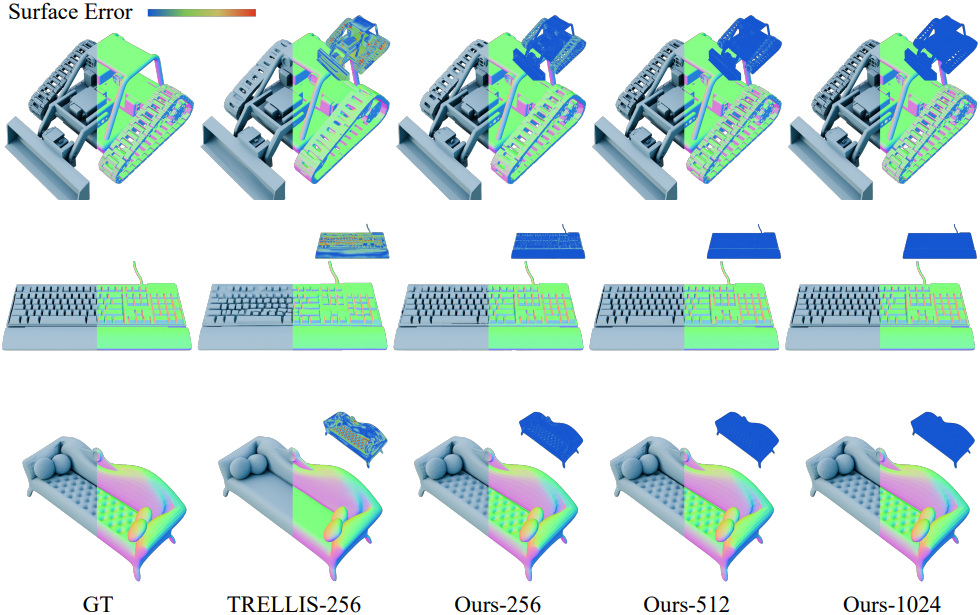
다음은 해상도에 따른 VAE 재구성 결과를 비교한 것이다.