[논문리뷰] Sparse DETR: Efficient End-to-End Object Detection with Learnable Sparsity
ICLR 2022. [Paper] [Github]
Byungseok Roh, JaeWoong Shin, Wuhyun Shin, Saehoon Kim
KakaoBrain | Lunit
29 Nov 2021
Introduction
다양한 object detection 방법이 제안되었으나 휴리스틱 방식으로 ground truth와 positive matching을 수행하는 기존 알고리즘은 거의 중복된 예측에 대한 NMS (non-maximum suppression) 후처리가 필요하다. 최근 세트 기반 목적 함수를 통해 NMS 후처리의 필요성을 제거하여 완전하게 end-to-end detector인 DETR이 소개되었다. 목적 함수는 분류 및 회귀 비용을 모두 고려하고 매우 경쟁력 있는 성능을 달성하는 Hungarian 알고리즘을 사용하여 설계되었다. 그러나 DETR은 작은 물체의 감지를 개선하기 위해 object detection에 일반적으로 사용되는 feature pyramid network와 같은 멀티스케일 feature를 사용할 수 없다. 주된 이유는 Transformer 아키텍처를 추가하여 메모리 사용과 계산량을 증가시켰기 때문이다. 결과적으로 작은 물체를 감지하는 능력이 상대적으로 떨어진다.
이 문제를 해결하기 위해 Deformable DETR 논문에서 deformable convolution에서 영감을 받은 deformable-attention이 제안되었고, attention 모듈의 key sparsification(희소화)를 통해 2차 복잡도를 선형 복잡도로 줄였다. Deformable DETR은 DETR의 느린 수렴과 높은 복잡도 문제를 해결하여 인코더가 멀티스케일 feature를 입력으로 사용할 수 있게 하였으며 작은 물체 감지 성능을 크게 향상시켰다. 그러나 멀티스케일 feature를 인코더 입력으로 사용하면 처리해야 할 토큰 수가 약 20배 증가한다. 결국 동일한 토큰 길이에 대한 효율적인 계산에도 불구하고 전체 복잡도가 다시 증가하여 모델 inference가 DETR보다 느려졌다.
일반적으로 자연 이미지는 관심 대상과 무관한 큰 배경 영역을 포함하는 경우가 많으며, 이에 따라 end-to-end detector에서는 배경에 해당하는 토큰도 상당 부분을 차지한다. 또한 각 지역 feature의 중요도는 동일하지 않으며, 이는 2-stage detector가 전경에만 집중하여 성공적으로 작업을 수행함을 통해 입증된다. 이는 detection task에서 줄일 수 있는 상당한 지역적 중복성이 존재하며 두드러지는 영역에 초점을 맞춘 효율적인 detector를 고안하는 것이 필요하고 자연스러운 방향임을 시사한다. 저자들은 예비 실험에서 다음을 관찰하였다.
- COCO validation 데이터셋에서 완전히 수렴된 Deformable DETR 모델을 inference하는 동안 디코더가 참조하는 인코더 토큰은 전체의 약 45%만 차지한다.
- 완전히 학습된 다른 detector에서 디코더가 선호하는 인코더 토큰만 업데이트하면서 새로운 detector를 재학습하면 성능 손실이 거의 발생하지 않는다 (0.1 AP 저하).
저자들은 이 관찰에서 영감을 받아 인코더 토큰을 sparsify하기 위해 학습 가능한 디코더 attention map predictor를 제안하였다. 기존 방법에서 인코더는 모든 토큰, 즉 해당 위치 임베딩과 결합된 backbone feature를 판별 없이 입력으로 사용한다. 한편, 본 논문의 접근 방식은 디코더에서 나중에 참조할 인코더 토큰을 구별하고 self-attention에서 해당 토큰만 고려한다. 따라서 이것은 계산에 관련된 인코더 토큰의 수를 크게 줄이고 총 계산 비용을 줄일 수 있다. 또한 계산 오버헤드를 최소화하면서 감지 성능을 향상시키기 위해 선택된 인코더 토큰에 대한 인코더 보조 loss를 제안한다. 제안된 보조 loss는 성능을 향상시킬 뿐만 아니라 더 많은 수의 인코더 레이어를 학습시킬 수 있다.
Approach
1. Preliminary
DETR
DETR은 backbone 네트워크에서 transformer 인코더로 flatten된 공간 feature map $x_\textrm{feat} \in \mathbb{R}^{N \times D}$를 가져온다. 여기서 $N$은 토큰, 즉 feature의 수를 나타내고 $D$는 토큰 차원을 나타낸다. 인코더는 여러 self-attention 모듈을 통해 $x_\textrm{feat}$를 반복적으로 업데이트한다. 그런 다음 transformer 디코더는 정제된 인코더 토큰 (즉, 인코더 출력)과 $M$개의 학습 가능한 object query \(\{q_i\}_{i=1 \cdots M}\)을 입력으로 사용하고 각 object query $q_i$에 대해 클래스 score $c \in [0, 1]^C$와 boundary box $b \in [0, 1]^4$의 튜플 \(\{\hat{y}_i\} = \{(c_i, b_i)\}\)를 예측한다. 여기서 $C$는 클래스 수이다. Backbone 네트워크를 포함한 모든 구성 요소는 ground truth \(\{y_i\}\)와 예측 \(\{\hat{y}_i\}\) 사이의 이분 매칭(bipartite matching)을 수행하여 공동으로 학습된다.
Deformable DETR
Deformable DETR은 DETR의 주요 계산 bottleneck인 attention 모듈을 deformable attention 모듈로 대체한다. 이는 계산 비용을 크게 줄이고 수렴을 향상시킨다. Query 세트 $\Omega_q$와 key 세트 $\Omega_k$의 크기가 같다고 가정하자.
\[\begin{equation} \vert \Omega_q \vert = \vert \Omega_k \vert = N \end{equation}\]기존의 attention은 모든 쌍 \(\{(q, k): q \in \Omega_q, k \in \Omega_k\}\)에 대한 attention 가중치 $A_{qk}$를 계산하여 $N$에 대한 2차 복잡도를 생성한다. Deformable attention은 각 query에 대한 관련 key만 고려하여 이 2차 복잡도를 선형 복잡도로 줄인다. 특히, deformable attention은 모든 query와 작은 key 세트에 대한 attention 가중치 $A_{qk}$를 계산한다.
\[\begin{equation} \{(q, k): q \in \Sigma_q, k \in \Sigma_{qk}\} \\ \textrm{where} \quad \Sigma_{qk} \subset \Sigma_k, \quad \vert \Sigma_{qk} \vert = K \ll N \end{equation}\]이 key sparsification로 인해 Deformable DETR은 backbone 네트워크의 멀티스케일 feature를 사용할 수 있어 작은 물체의 감지 성능을 크게 향상시켰다. 역설적이게도 멀티스케일 feature를 사용하면 transformer 인코더의 토큰 수가 DETR에 비해 약 20배 증가하여 인코더가 Deformable DETR의 계산 bottleneck이 된다. 이는 인코더의 토큰 수를 적극적으로 줄이기 위해 sparsification 방법을 개발하도록 동기를 부여한다.
2. Encoder Token Sparsification
인코더 모듈이 소수의 인코더 토큰을 선택적으로 정제하는 토큰 sparsification 체계를 도입한다. 이 인코더 토큰 부분집합은 특정 기준을 사용하여 backbone feature map $x_\textrm{feat}$에서 가져온다. 이 과정에서 업데이트되지 않는 feature의 경우 $x_\textrm{feat}$ 값이 변경되지 않고 인코더 레이어를 통과한다.
$x_\textrm{feat}$에서 각 토큰의 saliency를 측정하는 스코어링 네트워크 $g : \mathbb{R}^d \rightarrow \mathbb{R}$이 있다고 가정하자. 그런 다음 주어진 유지 비율 $\rho$에 대하여 score가 높은 상위 $\rho$% 토큰인 $ρ$-salient region $\Omega_s^\rho$를 정의한다.
\[\begin{equation} S = \vert \Omega_s^\rho \vert = \rho \cdot \vert \Omega_q \vert \ll \vert \Omega_q \vert = N \end{equation}\]그러면 $i$번째 인코더 레이어는 다음과 같이 feature $x_{i−1}$을 업데이트한다.
\[\begin{equation} x_i^j = \begin{cases} x_{i-1}^j & \quad j \notin \Omega_s^\rho \\ \textrm{LN} (\textrm{FFN} (z_i^j) + z_i^j) & \quad j \in \Omega_s^\rho \end{cases} \\ \textrm{where} \quad z_i^j = \textrm{LN}(\textrm{DefAttn} (x_{i-1}^j, x_{i-1}) + x_{i-1}^j) \end{equation}\]여기서 $\textrm{DefAttn}$은 deformable attention, $\textrm{LN}$은 layer normalization, $\textrm{FFN}$은 피드포워드 네트워크를 나타낸다. 선택되지 않은 토큰의 경우에도 값은 여전히 인코더 레이어를 통해 전달되므로 선택한 토큰을 업데이트할 때 key로 참조할 수 있다. 이는 선택되지 않은 토큰이 계산 비용을 최소화하면서 자체 가치를 잃지 않고 선택한 토큰에 정보를 전달할 수 있음을 의미한다. 여기서 $\Omega_s^\rho$로 토큰을 정제하기 위해 deformable attention을 사용하지만, 제안된 인코더 토큰 sparsification은 인코더가 어떤 attention 방법을 사용하든 관계없이 적용 가능하다.
Complexity of Attention Modules in Encoder

Deformable DETR은 key sparsification을 통해 attention 복잡도를 줄이고 위 그림과 같이 query sparsification을 통해 attention 복잡도를 더 줄인다. Deformable attention에는 선형 복잡도 $O(NK)$가 필요하다. 여기서 $K \ll N$는 각 query의 key 수이다. 반면 sparse attention에는 $O(SK)$만 필요하다. 여기서 $S \ll N$은 salient encoder query의 수이다.
3. Finding Salient Encoder Tokens
Backbone feature $x_\textrm{feat}$에서 $\Omega_s^\rho$를 찾기 위해 transformer 디코더에서 cross attention map을 사용하여 saliency를 결정한다. 별도의 detection head에서 얻은 objectness score를 기반으로 간단하면서도 효과적인 방법을 사용할 수 있다. 하지만 이 간단한 접근 방식의 한계는 고급 방식을 개발하도록 동기를 부여하였다.
Objectness Score
Transformer 인코더에서 backbone feature의 어떤 항목을 추가로 업데이트해야 하는지 결정하기 위해 인코더의 각 입력 토큰 $x_\textrm{feat}$마다 objectness를 측정하는 것은 매우 자연스러운 일이다. 사전 학습된 backbone network의 feature map이 개체의 saliency를 찾을 수 있다는 것은 널리 알려져 있으며, 이것이 Region Proposal Network (RPN)이 많은 object detector에 성공적으로 채택된 이유이다. 이 관찰에서 영감을 얻어 backbone feature map에 추가 detection head와 Hungarian loss를 도입한다. 여기서 새로 추가된 head의 구조는 디코더의 최종 detection head 중 하나와 동일하다. 그런 다음 가장 높은 클래스 score를 가진 상위 $\rho$% 인코더 토큰을 $\Omega_s^\rho$로 선택할 수 있다. 이 접근 방식은 인코더 토큰을 sparsify하는 데 효과적이지만 별도의 detection head에서 선택한 인코더 토큰이 디코더에 대해 명시적으로 고려되지 않기 때문에 transformer 디코더에 최선이 아니다.
Decoder Cross-Attention Map
더 명확한 방식으로 디코더와 관련성이 높은 인코더 토큰의 부분집합을 선택하는 또 다른 접근 방식을 고려한다. 학습이 계속됨에 따라 디코더가 개체를 감지하는 데 유리한 인코더 출력 토큰의 부분집합에 점진적으로 주의를 기울이기 때문에 transformer 디코더의 cross attention map이 saliency를 측정하는 데 사용될 수 있다. 이것에 동기를 부여하여 디코더 cross attention map에 의해 정의된 saliency의 ground-truth를 예측하는 스코어링 네트워크를 도입하고 이를 사용하여 어떤 인코더 토큰을 즉석에서 추가로 정제해야 하는지 결정한다. 아래 그림은 스코어링 네트워크를 학습하는 방법을 요약한 것이다.
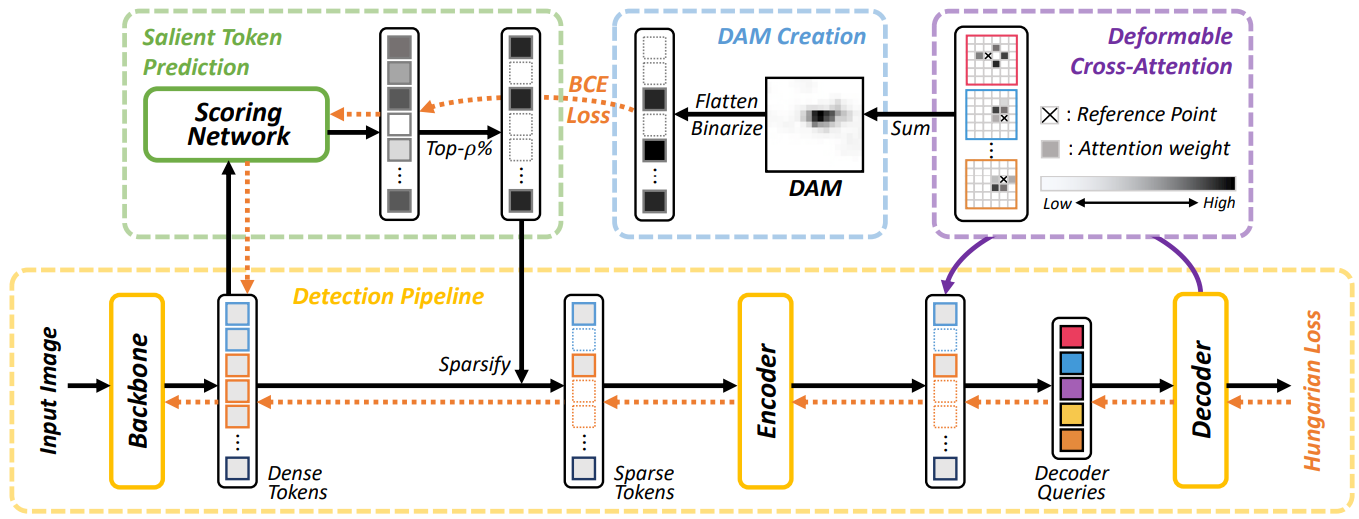
인코더의 각 입력 토큰 $x_\textrm{feat}$의 saliency를 결정하려면 모든 object query와 인코더 출력 간의 디코더 cross attention을 집계해야 한다. 이 과정은 backbone의 feature map과 동일한 크기의 단일 map인 Decoder crossAttention Map (DAM)을 생성한다. 일반 attention의 경우 모든 디코더 레이어의 attention map을 합산하여 DAM을 쉽게 얻을 수 있다. Deformable attention의 경우 각 인코더 토큰에 대해 attention 오프셋이 인코더 출력 토큰을 향하는 디코더 object query의 attention 가중치를 누적하여 해당 DAM 값을 얻을 수 있다.
스코어링 네트워크를 학습시키기 위해 인코더 토큰의 상위 $\rho$% (attention 가중치 기준)만 유지되도록 DAM을 이진화(binarize)한다. 이는 디코더가 각 인코더 토큰을 얼마나 많이 참조할지 정확하게 예측하는 것이 목표가 아니라 디코더가 가장 많이 참조하는 인코더 토큰의 작은 부분 집합을 찾는 것이기 목표기 때문이다. 이 이진화된 DAM은 각 인코더 토큰이 가장 많이 참조되는 상위 $rho$% 인코더 토큰에 포함되는지 여부를 나타내는 one-hot 타겟을 의미한다. 그런 다음 4-layer 스코어링 네트워크 $g$로 주어진 인코더 토큰이 가장 많이 참조되는 상위 $rho$% 토큰에 포함될 가능성을 예측하고 이진화된 DAM과 예측 사이의 BCE (Binary Cross Entropy) loss를 최소화하여 네트워크를 학습시킨다.
\[\begin{equation} \mathcal{L}_\textrm{dam} = - \frac{1}{N} \sum_{i=1}^N \textrm{BCE} (g (x_\textrm{feat})_i, \textrm{DAM}_i^\textrm{bin}) \end{equation}\]여기서 \(\textrm{DAM}_i^\textrm{bin}\)는 $i$번째 인코더 토큰의 이진화된 DAM 값을 의미한다.
학습 초기 단계의 DAM이 정확하지 않기 때문에 디코더의 결과를 기반으로 인코더 토큰을 잘라내는 것은 최종 성능을 저하시키거나 수렴을 저해한다. 그러나 최적화가 학습 초기 단계에서도 매우 안정적이며 objectness score 기반 방법에 비해 더 나은 성능을 달성한다.
4. Additional Components
두 가지 추가 구성 요소를 도입한다.
- 인코더 토큰의 보조 loss
- Top-$k$ 디코더 쿼리 선택
두 구성 요소는 최종 성능을 개선하고 최적화를 안정화하는 데 크게 도움이 된다. 이러한 구성 요소를 포함하는 Sparse DETR의 전체 아키텍처는 아래 그림에 나와 있다.
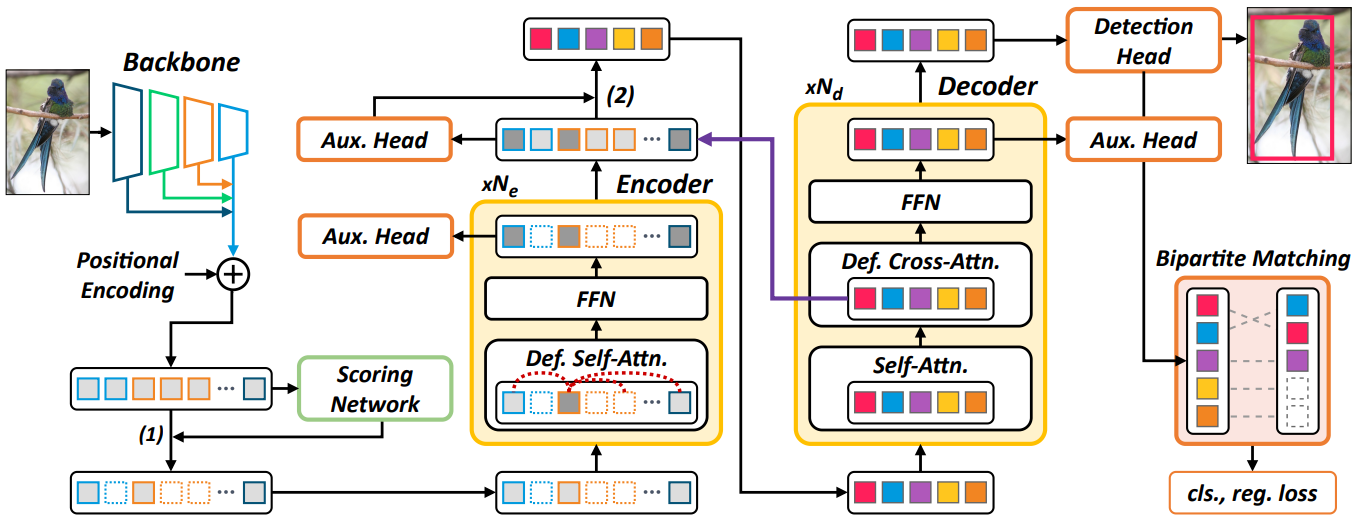
Encoder Auxiliary Loss
DETR 변형에서 보조 detection head는 디코더 레이어에 연결되지만 인코더 레이어에는 연결되지 않는다. 디코더 토큰 (약 300개)에 비해 상당히 많은 수의 인코더 토큰 (약 18,000개)으로 인해 인코더 보조 head는 계산 비용을 크게 증가시킨다. 그러나 Sparse DETR에서는 인코더 토큰의 일부만 인코더에 의해 정제되며 sprasify된 인코더 토큰에 대해서만 보조 head를 추가하는 것은 큰 부담이 되지 않는다.
선택한 토큰에 Hungarian loss와 함께 보조 detection head를 적용하면 기울기 소실 (vanishing gradient) 문제를 완화하여 더 깊은 인코더의 수렴을 안정화하고 감지 성능을 향상시킨다. 중간 레이어에 Hungarian loss를 적용하면 인코더의 혼란스러운 feature를 구별하는 데 도움이 되며 최종 head의 감지 성능에 기여한다.
Top-$k$ Decoder Queries
DETR과 Deformable DETR에서 decoder query는 학습 가능한 object query로만 제공되거나 인코더 뒤의 다른 head를 통해 예측된 기준점과 함께 제공된다. Efficient DETR에서 디코더는 RoI Pooling과 유사하게 인코더 출력의 일부를 입력으로 사용한다. 여기서 인코더 출력 $x_\textrm{enc}$에는 보조 detection head가 부착되어 있으며 head는 각 인코더 출력의 objectness score를 계산한다. Score를 기반으로 top-$k$ 인코더 출력은 objectness score 기반 인코더 토큰 sparsification과 유사하게 decoder query로 전달된다. 이것은 학습 가능한 object detection 또는 2-stage 방식을 기반으로 하는 방법보다 성능이 우수하므로 최종 아키텍처에 이 top-$k$ decoder query 선택을 포함한다.
Experiments
- 구현 디테일
- ResNet-50과 Swin Transformer를 사전 학습된 backbone으로 사용
- 각각 끝에 보조 head를 가진 인코더 레이어 6개와 디코더 레이어 6개를 쌓음
- Batch size: 16
- Epochs: 50
- Learning rate: 초기에 0.0002, 40 epochs마다 1/10
- 나머지 hyperparameter는 Deformable DETR과 동일
1. Comparison with Object Detection Baselines
다음은 COCO 2017 val set에서의 감지 성능을 비교한 표이다.
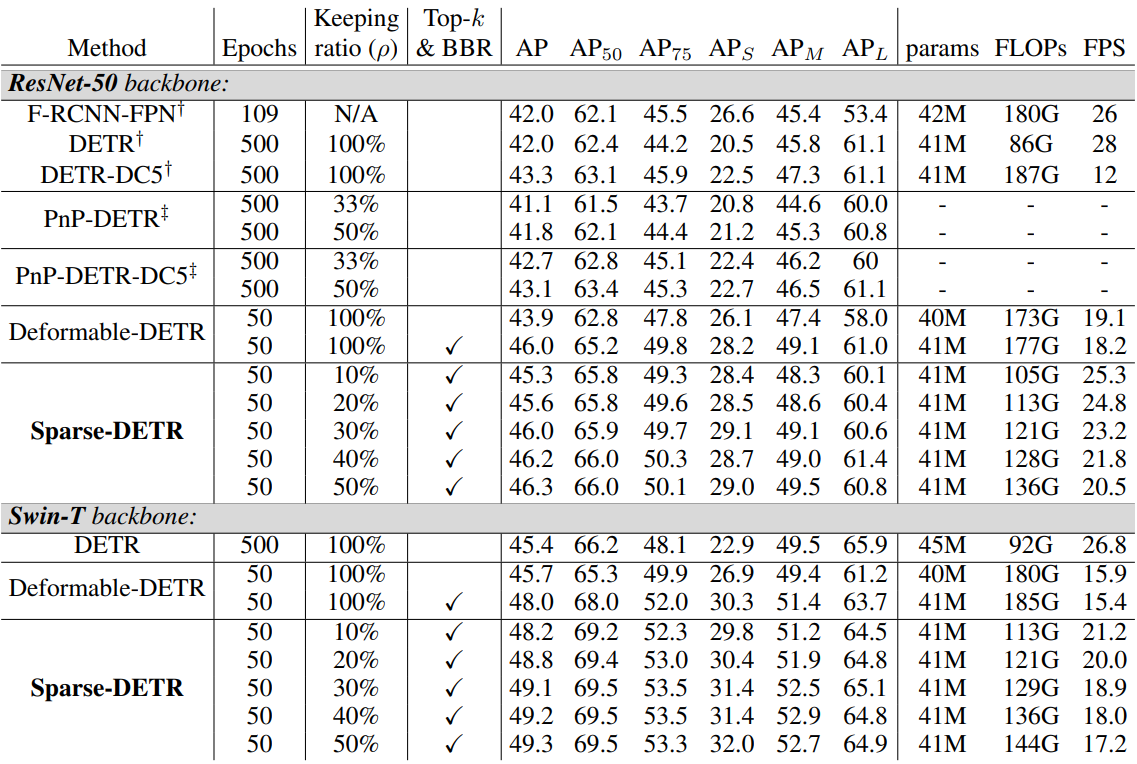
2. Comparison between Token Selection Criteria
다음은 토큰 선택 방법에 따른 성능을 나타낸 그래프이다. OS는 Objectness Score를 뜻한다.
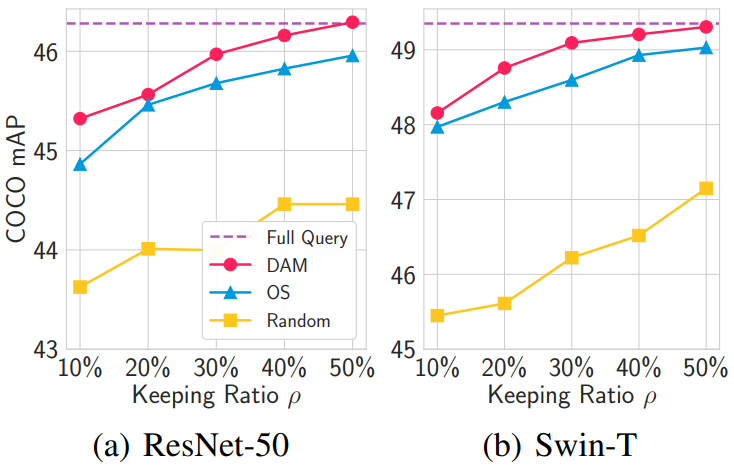
저자들은 DAM 기반 모델이 다른 모델보다 우수한 이유를 분석하기 위해 디코더가 참조하는 인코더 토큰과 인코더가 정제한 토큰 간의 중첩을 측정하였다. 메트릭으로 스칼라 상관계수 $Corr$을 다음과 같이 계산한다.
여기서 $\Omega_D$는 디코더가 참조하는 인코더 토큰 집합이고 $\textrm{DAM}_x$는 토큰 $x$에 해당하는 DAM 값이다. 이 $Corr$ 지표는 디코더가 참조하는 토큰 중 인코더가 연마한 토큰의 비율을 나타낸다.
다음은 DAM 기반 모델과 OS 기반 모델의 $Corr$ 지표를 비교한 그래프이다.

3. Effectiveness of the Encoder Auxiliary Loss
다음은 인코더 레이어 수에 대한 ablation study 결과이다.
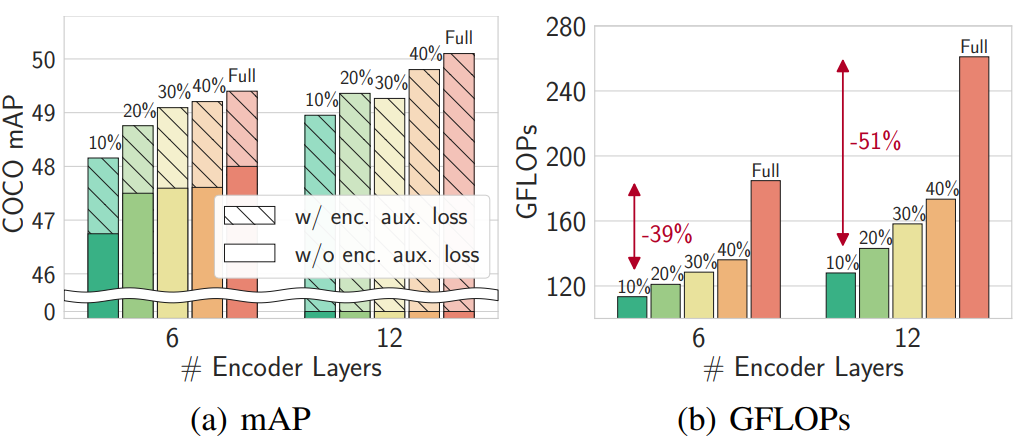
인코더 보조 loss는 감지 성능을 향상시킬 뿐만 아니라 인코더 레이어가 12개로 두 배가 됨에 따라 감지 성능을 지속적으로 향상시킨다. 더 많은 인코더 레이어를 쌓을수록 디코더 cross attention을 통해 전파되는 기울기가 사라지므로 보조 loss의 중간 기울기가 필요하다.
4. Dynamic Sparsification for Inference Stage
실제 애플리케이션의 다양한 하드웨어 조건에서 모델을 배포하려면 필요한 성능-계산 trade-off에 따라 다양한 규모로 모델을 재학습해야 하는 경우가 많다. 저자들은 고정된 sparsity로 학습된 모델이 inference 시 동적 sparsity에 잘 적응할 수 있는지 평가하여 Sparse DETR이 이러한 번거로움을 피할 수 있는지 확인하였다. 아래 그림은 DAM 기반 방법으로 Swin-T backbone과 30% 인코더 토큰을 사용하여 모델을 학습시켰을 때 inference 동안 다양한 $\rho$ 하에서의 성능을 보여준다.
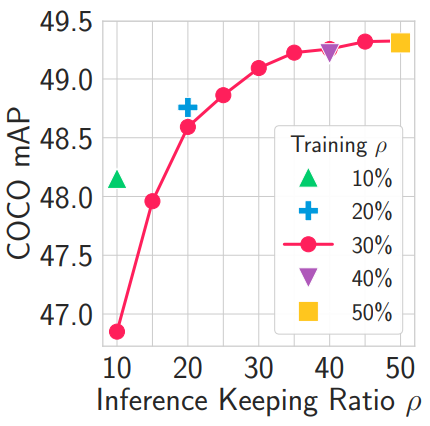
Inference 시 $\rho$가 작을 경우 동적 sparsification의 성능이 다소 떨어지지만 단일 모델만 사용한다는 점에서 다양한 $\rho$에서 전반적인 성능은 만족스럽다.