[논문리뷰] Spacetime Gaussian Feature Splatting for Real-Time Dynamic View Synthesis
CVPR 2024. [Paper] [Page] [Github]
Zhan Li, Zhang Chen, Zhong Li, Yi Xu
OPPO US Research Center | Portland State University
28 Dec 2023

Introduction
정적 장면에서의 성공에도 불구하고 NeRF나 3D Gaussian Splatting (3DGS)를 동적 장면에 직접 적용하는 것은 모델 크기 및 학습 시간의 오버헤드로 인해 어렵다. SOTA 동적 뷰 합성 방법은 단일 모델에서 여러 프레임이 표현되는 접근 방식을 채택하였다.
NeRFPlayer와 HyperReel은 정적인 공간적 표현과 시간적 feature의 공유 및 보간을 결합하여 모델의 압축성을 향상시켰다. 이 전략은 동영상의 인접 프레임이 일반적으로 높은 유사성을 나타내는 특성을 활용한다. 비슷한 맥락에서 MixVoxels는 시간에 따라 변하는 latent를 사용하고 이를 내적으로 공간적 feature와 연결하였다. K-Planes과 HexPlane은 간결한 표현을 위해 4D 시공간 영역을 여러 2D 평면으로 분해하였다. 이러한 방법의 한 가지 한계점은 그리드와 같은 표현이 장면 구조의 역학에 완전히 적응할 수 없어 섬세한 디테일의 모델링을 방해한다는 것이다. 동시에 품질 저하 없이 실시간 고해상도 렌더링을 생성하는 데 어려움을 겪고 있다.
본 논문에서는 동적 뷰 합성을 위한 새로운 표현을 제시하였다. 본 논문의 접근 방식은 사실적인 품질, 실시간 고해상도 렌더링, 컴팩트한 모델 크기를 동시에 달성하였다. 핵심은 3D Gaussian을 4D 시공간 영역으로 확장하는 Spacetime Gaussian (STG)이다. 다항식으로 parameterize된 모션 및 회전과 함께 시간에 따른 불투명도를 3D Gaussian에 장착한다. 결과적으로 STG는 장면의 정적, 동적, 일시적 콘텐츠를 충실하게 모델링할 수 있다.
저자들은 모델의 컴팩트함을 강화하고 시간에 따라 변하는 외형을 고려하기 위해 splatted feature rendering을 제안하였다. 구체적으로 각 Spacetime Gaussian에 대해 spherical harmonics (SH) 계수를 저장하는 대신 base color, 뷰 관련 정보, 시간 관련 정보를 인코딩하는 feature를 저장한다. 이러한 feature는 미분 가능한 스플래팅을 통해 이미지 공간으로 rasterize되고 작은 MLP 네트워크를 거쳐 최종 색상을 생성한다. SH에 비해 크기는 작지만 강력한 표현력을 발휘한다.
또한 복잡한 장면의 렌더링 품질을 향상시키기 위해 Gaussian의 guided sampling을 도입하였다. Initialization 시 Gaussian으로 드물게 덮힌 먼 영역은 렌더링 결과가 흐릿해지는 경향이 있다. 이 문제를 해결하기 위해 학습 오차와 대략적인 깊이를 바탕으로 4D 장면에서 새로운 Gaussian을 샘플링한다.
Method
1. Spacetime Gaussians
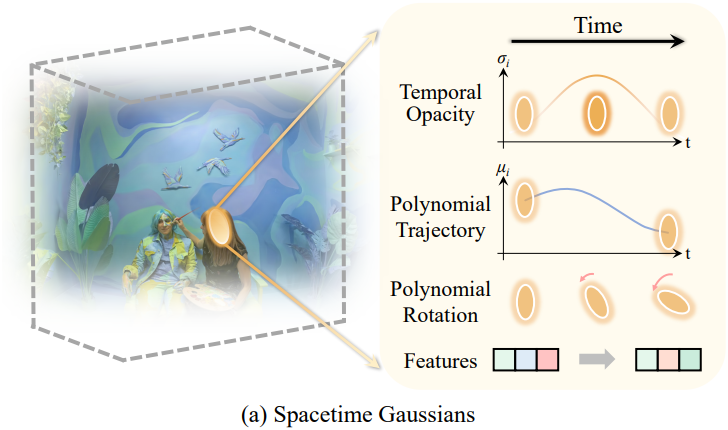
본 논문은 4D 동역학을 표현하기 위해 3D Gaussian과 시간 성분을 결합하여 나타나고 사라지는 콘텐츠와 모션/변형을 모델링하는 Spacetime Gaussians (STG)를 제안하였다. 구체적으로, 시간적 불투명도를 인코딩하기 위해 temporal radial basis function를 도입하였다. 이는 나타나거나 사라지는 장면 콘텐츠를 효과적으로 모델링할 수 있다. 한편, 시간을 조건으로 하는 3D Gaussian의 위치와 회전에 대한 파라메트릭 함수를 활용하여 장면의 모션과 변형을 모델링한다. 시공간 지점 $(\textbf{x}, t)$에서의 STG의 불투명도는 다음과 같다.
여기서 $\sigma_i (t)$는 시간적 불투명도이고, $\mu_i (t)$와 $\Sigma_i (t)$는 시간에 의존하는 위치 및 공분산이다. $i$는 $i$번째 STG를 뜻한다.
Temporal Radial Basis Function. 시간 $t$에서 STG의 시간 불투명도를 나타내기 위해 temporal radial basis function을 사용한다. 시간적 불투명도 $\sigma_i (t)$에 대해 1D Gaussian을 사용한다.
\[\begin{equation} \sigma_i (t) = \sigma_i^s \exp (-s_i^\tau \vert t - \mu_i^\tau \vert^2) \end{equation}\]여기서 temporal center $\mu_i^\tau$는 STG가 가장 잘 보이는 타임스탬프를 나타내고, temporal scaling factor $s_i^\tau$는 유효한 지속 기간을 결정한다. STG 전반에 걸쳐 공간적 불투명도 변화를 허용하기 위해 시간에 독립적인 공간적 불투명도 $\sigma_i^s$를 포함한다.
Polynomial Motion Trajectory. 각 STG에 대해 다항 함수를 사용하여 모션을 모델링한다.
\[\begin{equation} \mu_i (t) = \sum_{k=0}^{n_p} b_{i,k} (t - \mu_i^\tau)^k \end{equation}\]다항식 계수 $b_{i,k} \in \mathbb{R}$은 학습 중에 최적화된다.
Polynomial Rotation. 모션 궤적과 유사하게 rotation matrix $R_i$의 쿼터니언을 표현하기 위해 다항 함수를 사용한다.
\[\begin{equation} q_i (t) = \sum_{k=0}^{n_q} c_{i,k} (t - \mu_i^\tau)^k \end{equation}\]Scaling matrix $S_i$는 시간에 독립적으로 둔다.
2. Splatted Feature Rendering
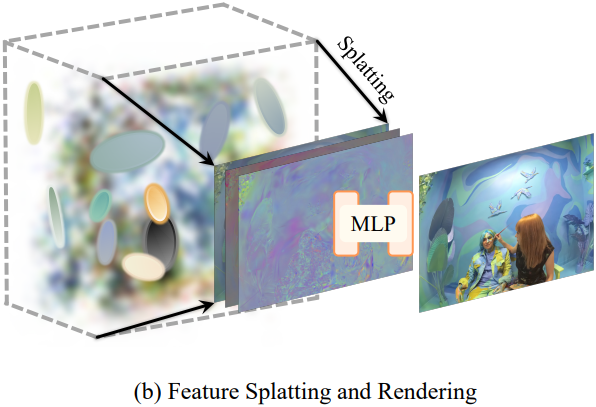
뷰와 시간에 따른 radiance를 정확하고 간결하게 인코딩하기 위해 각 STG에 spherical harmonics (SH) 계수 대신 feature를 저장한다. 구체적으로 각 STG의 feature \(\textbf{f}_i (t) \in \mathbb{R}^9\)는 세 부분으로 구성된다.
\(\textbf{f}_i^\textrm{base} \in \mathbb{R}^3\)는 RGB base color를 포함하고, \(\textbf{f}_i^\textrm{dir}, \textbf{f}_i^\textrm{time} \in \mathbb{R}^3\)는 뷰 방향과 시간에 관련된 정보를 인코딩한다.
Feature splatting 프로세스는 RGB 색상이 feature \(\textbf{f}_i (t)\)로 대체된다는 점을 제외하면 Gaussian Splatting과 유사하다. 이미지 공간으로 splatting한 후 각 픽셀의 splatting된 feature를 \(\textbf{F}^\textrm{base}\), \(\textbf{F}^\textrm{dir}\), \(\textbf{F}^\textrm{time}\)로 분할한다. 각 픽셀의 최종 RGB 색상은 2-layer MLP $\Phi$를 거친 후 얻어진다.
\[\begin{equation} \textbf{I} = \textbf{F}^\textrm{base} + \Phi (\textbf{F}^\textrm{dir}, \textbf{F}^\textrm{time}, \textbf{r}) \end{equation}\]여기서 $\textbf{r}$은 뷰 방향이며, feature들과 concatenate되어 $\Phi$에 입력된다.
SH 인코딩과 비교하여 feature 기반 접근 방식은 각 STG에 대해 더 적은 파라미터를 필요로 한다. 동시에 MLP 네트워크 $\Phi$는 얕고 좁기 때문에 여전히 렌더링 속도가 빠르다.
렌더링 속도를 최대화하기 위해 선택적으로 $\Phi$를 삭제하고 학습 및 렌더링 중에 $\textbf{F}^\textrm{base}$만 유지할 수도 있다. 이 구성을 라이트 버전이라고 부른다.
3. Optimization
MLP $\Phi$와 각 STG의 파라미터 \((\sigma_i^s, s_i^\tau, \mu_i^\tau, \{b_{i,k}\}_{k=0}^{n_p}, \{c_{i,k}\}_{k=0}^{n_q}, \textbf{s}_i, \textbf{f}_i^\textrm{base}, \textbf{f}_i^\textrm{dir}, \textbf{f}_i^\textrm{time})\)가 최적화된다.
3DGS와 마찬가지로 미분 가능한 스플래팅과 기울기 기반 역전파를 통해 이러한 파라미터를 최적화하고 중간에 density control을 진행한다. 렌더링된 이미지를 GT 이미지와 비교하는 렌더링 loss를 사용한다. 렌더링 loss는 L1 항과 D-SSIM 항으로 구성된다.
4. Guided Sampling of Gaussians
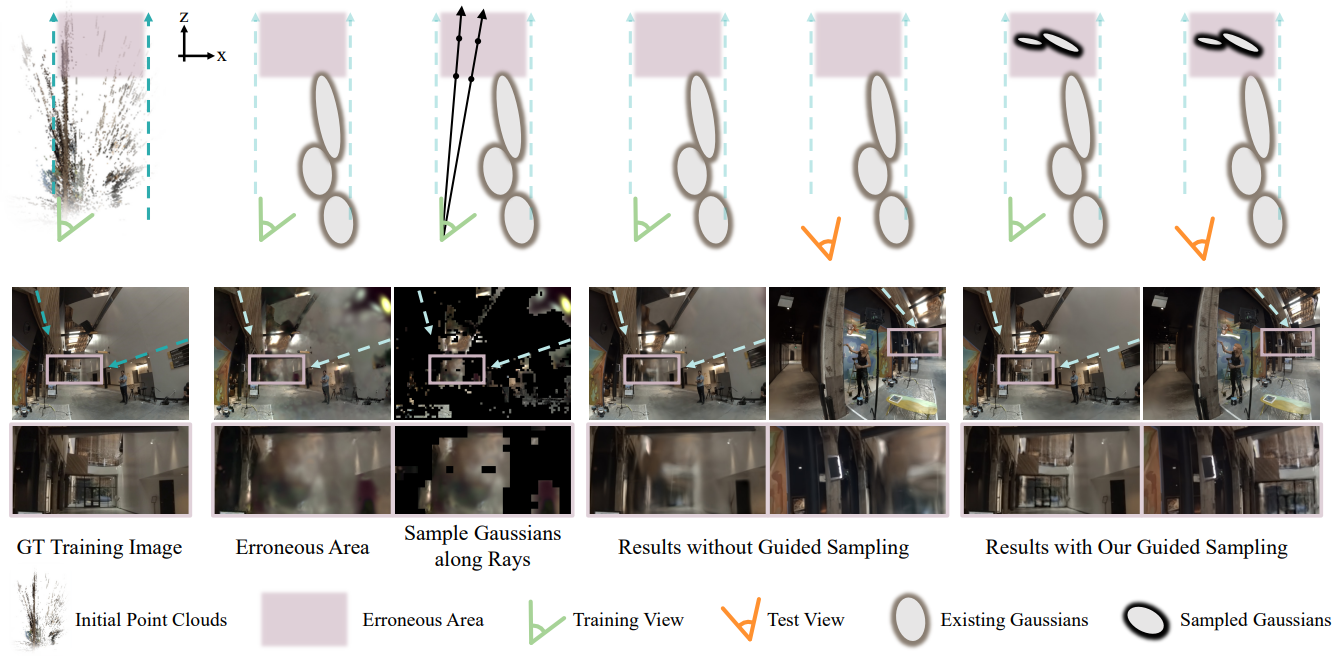
저자들은 initialization 시 Gaussian이 희박한 영역의 렌더링 품질이 높게 수렴되기 어렵다는 것을 관찰했다. 특히 이러한 영역이 카메라에서 멀리 떨어져 있는 경우 더욱 그렇다. 따라서 학습 오차와 coarse한 깊이를 guidance로 새로운 Gaussian을 샘플링하는 전략을 추가로 도입하였다.
학습 중 오차가 큰 픽셀의 광선을 따라 새로운 Gaussian들을 샘플링한다. 샘플링 효율성을 보장하기 위해 loss가 안정된 후에 샘플링을 수행한다. 오차 맵은 학습 중에 노이즈가 있을 수 있으므로 patch-wise로 학습 오차를 집계하여 상당한 오차가 있는 영역에 우선순위를 둔다. 그런 다음 큰 오차가 있는 각 패치의 중앙 픽셀에서 광선을 샘플링한다. 지나치게 큰 깊이 범위에서 샘플링을 피하기 위해 Gaussian 중심의 coarse한 depth map을 활용하여 보다 구체적인 깊이 범위를 결정한다. Depth map은 feature splatting 중에 생성되며 계산 오버헤드가 거의 발생하지 않는다. 그런 다음 새로운 Gaussian들은 광선을 따라 깊이 범위 내에서 균일하게 샘플링된다. 새로 샘플링된 Gaussian들의 중심에 작은 노이즈를 추가한다. 샘플링된 Gaussian들 중에서 불필요한 것들은 학습 중에 불투명도가 낮아져 제거된다. 샘플링 프로세스는 3회 이하로만 수행하면 된다.
제안된 guided sampling 전략은 3DGS의 density control을 보완한다. Density control은 기존 Gaussian들 근처에서 점진적으로 Gaussian을 증가시키는 반면, 제안된 접근 방식은 Gaussian이 희박하거나 없는 영역에서 새로운 Gaussian을 샘플링할 수 있다.
Experiments
- 구현 디테일
- $n_p = 3$, $n_q = 1$
- optimizer: Adam
- 사용 가능한 모든 타임스탬프의 SfM 포인트 클라우드를 사용하여 STG를 초기화
- Density control의 경우 3DGS보다 더 공격적인 pruning을 수행하여 Gaussian 수를 줄이고 모델 크기를 작게 유지
- 50 프레임 시퀀스를 학습시키는 데 NVIDIA A6000 GPU 1개에서 40 ~ 60분 소요
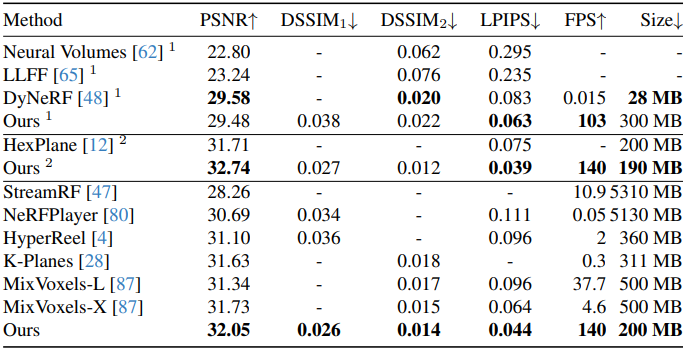
1. Neural 3D Video Dataset

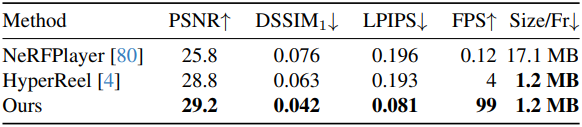
2. Google Immersive Dataset

3. Technicolor Dataset

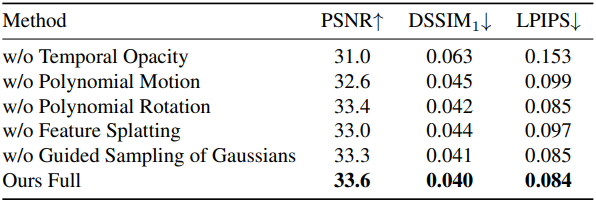
4. Ablation Study
다음은 구성 요소에 대한 ablation 결과이다.
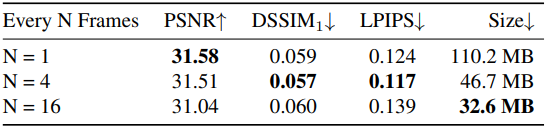
다음은 SfM 포인트 클라우드가 initialization에 사용되는 프레임 수에 대한 ablation 결과이다.