[논문리뷰] Score Jacobian Chaining: Lifting Pretrained 2D Diffusion Models for 3D Generation

CVPR 2023. [Paper] [Page]
Haochen Wang, Xiaodan Du, Jiahao Li, Raymond A. Yeh, Greg Shakhnarovich
TTI-Chicago | Purdue University
1 Dec 2022

Introduction

본 논문은 3D 데이터에 대한 접근 없이도 이미지로 사전 학습된 2D diffusion model을 radiance field의 3D 생성 모델로 변환하는 방법을 소개한다. 핵심 통찰력은 diffusion model을 score function이라고 하는 gradient field의 학습된 predictor로 해석하는 것이다. 본 논문의 방법은 추정된 score에 chain rule을 적용하므로 Score Jacobian Chaining (SJC)이라 부른다.

자연스럽게 제기되는 질문은 학습된 gradient에 chain rule을 적용할 수 있는지 여부이다. 이미지에 대한 diffusion model을 고려하자. 이미지 $x$는 파라미터 $\theta$를 갖는 어떤 함수 $f$ 의해 parameterize될 수 있다 ($x = f(\theta)$). Jacobian $\frac{\partial x}{\partial \theta}$를 통해 chain rule을 적용하면 이미지 $x$의 gradient가 파라미터 $\theta$의 gradient로 변환된다. 본 논문에서는 $f$를 미분 가능한 renderer로 선택하여 3D와 멀티뷰 2D 간의 연결을 탐구하는 데 관심이 있으며, 이를 통해 사전 학습된 2D 리소스만을 사용하여 3D 생성 모델을 만든다.

여러 3D 에셋의 공통점은 2D 이미지로 렌더링할 수 있다는 것이다. 미분 가능한 renderer는 카메라 시점 $\pi$에서 3D 에셋 $\theta$를 렌더링한 이미지 $x_\pi$의 Jacobian $J_\pi = \frac{\partial x_\pi}{\partial \theta}$를 제공한다. SJC는 미분 가능한 렌더링을 사용하여 여러 시점에서 2D 이미지 gradient를 3D gradient로 집계하고 생성 모델을 2D에서 3D로 끌어올린다. 3D 에셋 $\theta$를 voxel에 저장된 radiance field로 parameterize하고 volume rendering 함수로 $f$를 선택한다.

핵심 문제는 렌더링된 이미지 $x_\pi$에서 diffusion model을 직접 평가하여 2D score를 계산하면 out-of-distribution (OOD) 문제가 발생한다는 것이다. 일반적으로 diffusion model은 denoiser로 학습되고 학습 중에 noise가 있는 입력만 보았다. 반면에, 최적화 중에 noise가 없는 렌더링된 이미지에 대한 denoiser를 평가해야 하며, 이는 OOD 문제로 이어진다. 본 논문은 이 문제를 해결하기 위해 noise가 없는 이미지에 대한 score를 추정하는 접근 방식인 Perturb-and-Average Scoring을 제안하였다.

Preliminaries

1. Denoising score matching

\(p_\textrm{data}\)에서 추출한 샘플의 데이터셋 \(\mathcal{Y} = \{y_i\}\)이 주어지면 diffusion model은 주로 noise가 추가된 샘플 $y + \sigma_n$과 $y$ 사이의 차이를 최소화하여 denoiser $D$를 학습한다.

\[\begin{equation} \mathbb{E}_{y \sim p_\textrm{data}} \mathbb{E}_{n \sim \mathcal{N}(0,I)} \| D (y + \sigma n; \sigma) - y \|_2^2 \end{equation}\]

즉, $D$는 입력 $y + \sigma n$의 noise를 제거한다. 2D 이미지의 경우 $D$는 일반적으로 ConvNet으로 선택된다. DDPM은 대신 noise residual $\hat{\epsilon}$를 예측하며, denoiser 형태로 다시 변환될 수 있다.

\[\begin{equation} D(x; \sigma) = x - \sigma \hat{\epsilon} (x) \end{equation}\]

본 논문에서는 사전 학습된 diffusion model을 denoiser로 취급한다.

2. Score from denoiser

$p_\sigma (x)$를 표준 편차 $\sigma$의 Gaussian noise가 더해진 데이터 분포라 하자. 학습된 denoiser $D$는 denoising score에 대한 좋은 근사값을 제공한다.

\[\begin{equation} \nabla_x \log p_\sigma (x) \approx \frac{D(x; \sigma) - x}{\sigma^2} \end{equation}\]

DDPM은 다양한 \(\sigma \in \{\sigma_i\}_{i=1}^T\)에서 noise 분포 $p_\sigma (x)$의 score function을 추정한다. 샘플링을 수행하기 위해 diffusion model은 $\sigma_T > \cdots > \sigma_0 = 0$의 noise level 시퀀스를 통해 샘플을 점진적으로 업데이트한다.

3. Score as mean-shift

Score는 mean-shift처럼 동작한다. $p_\textrm{data}$를 샘플 \(\{y_i\}\)에 대한 경험적 데이터 분포로 단순화하면 noise level $\sigma$에서 $p_\sigma (x)$는 mixture of Gaussians 형태를 취한다.

\[\begin{equation} p_\sigma (x) = \mathbb{E}_{y \sim p_\textrm{data}} \mathcal{N} (x; y, \sigma^2 I) \end{equation}\]

이 경우 최적의 denoiser에 대한 closed-form 식이 존재한다.

\[\begin{equation} D(x; \sigma) = \frac{\sum_i \mathcal{N} (x; y_i, \sigma^2 I) y_i}{\sum_i \mathcal{N} (x; y_i, \sigma^2 I)} \end{equation}\]

즉, $D(x; \sigma)$는 bandwidth이 $\sigma$인 Gaussian kernel 하에서 $x$ 주변의 데이터 샘플 \(\{y_i\}\)의 로컬한 가중 평균이다. Denoising score function은 weighted nearest neighbors로 이동하기 위해 $x$를 업데이트하기 위한 가이드로 생각할 수 있다.

Score Jacobian Chaining for 3D Generation

$\theta$를 3D 에셋의 파라미터라 하자. 본 논문의 목표는 분포 $p(\theta)$를 모델링하고 샘플링하여 3D 장면을 생성하는 것이며, 이미지 $p(x)$에서 사전 학습된 2D diffusion model만 주어지고 3D 데이터에 접근할 수 없다. 2D 분포 $p(x)$와 3D 분포 $p(\theta)$를 연관시키기 위해, 3D 에셋 $\theta$의 확률 밀도가 카메라 포즈 $\pi$에 대한 2D 이미지 렌더링 $x_\pi$의 확률 밀도 기대값에 비례한다고 가정한다.

\[\begin{equation} p_\sigma (\theta) = \frac{1}{Z} \mathbb{E}_\pi [p_\sigma (x_\pi (\theta))] \\ \textrm{where} \; Z = \int \mathbb{E}_\pi [p_\sigma (x_\pi (\theta))] d \theta \end{equation}\]

Jensen’s inequality를 사용하여 위 식의 분포에 대한 하한 $\log \tilde{p}_\sigma (\theta)$를 설정하면 다음과 같다.

\[\begin{aligned} \log p_\sigma (\theta) &= \log [\mathbb{E}_\pi (p_\sigma (x_\pi))] - \log Z \\ &\ge \mathbb{E}_\pi [\log p_\sigma (x_\pi)] - \log Z = \log \tilde{p}_\sigma (\theta) \end{aligned}\]

Score는 데이터의 로그 확률 밀도의 기울기이다. Chain rule에 의해 다음 식이 성립한다.

\[\begin{aligned} \nabla_\theta \log \tilde{p}_\sigma (\theta) &= \mathbb{E}_\pi [\nabla_\theta \log p_\sigma (x_\pi)] \\ \frac{\partial \log \tilde{p}_\sigma (\theta)}{\partial \theta} &= \mathbb{E}_\pi \bigg[ \frac{\partial \log p_\sigma (x_\pi)}{\partial x_\pi} \cdot \frac{\partial x_\pi}{\partial \theta} \bigg] \\ \underbrace{\nabla_\theta \log \tilde{p}_\sigma (\theta)}_{\textrm{3D score}} &= \mathbb{E}_\pi [\underbrace{\nabla_{x_\pi} \log p_\sigma (x_\pi)}_{\textrm{2D score; pretrained}} \cdot \underbrace{J_\pi}_{\textrm{renderer Jacobian}}] \end{aligned}\]

1. Computing 2D Score on Non-Noisy Images

위 식에서 3D score를 계산하려면 $x_\pi$에 대한 2D score가 필요하다. 첫 번째 시도는 denoiser에서 score를 직접 적용하는 것이다.

\[\begin{equation} \textrm{score} (x_\pi, \sigma) = \frac{D(x_\pi; \sigma) - x_\pi}{\sigma^2} \end{equation}\]

하지만, 사전 학습된 denoiser $D$를 $x_\pi$에서 평가하면 out-of-distribution (OOD) 문제가 발생한다. $D$는 학습 시에 분포 $y + \sigma n$의 noisy한 입력만 보았다 ($y \sim p_\textrm{data}$, $n \sim \mathcal{N}(0,I)$). 그러나 3D 에셋 $\theta$에서 렌더링된 이미지 $x_\pi$는 일반적으로 이러한 분포와 일치하지 않는다.

위 그림은 FFHQ에서 사전 학습한 denoiser가 주어졌을 때, 출력 $D(x_\textrm{blob}; \sigma = 6.5)$를 시각화한 것이다. $D$가 weighted nearest neighbors를 예측한다는 직관에 따라, denoiser가 주황색 얼룩을 얼굴 매니폴드와 혼합할 것으로 예상되었다. 하지만, 실제로 이 score \((D(x_\textrm{blob}; \sigma) − x_\textrm{blob})/\sigma^2\)로 업데이트할 때 선명한 아티팩트를 관찰하고 이미지가 얼굴 매니폴드에서 더 멀어진다.

Perturb-and-Average Scoring

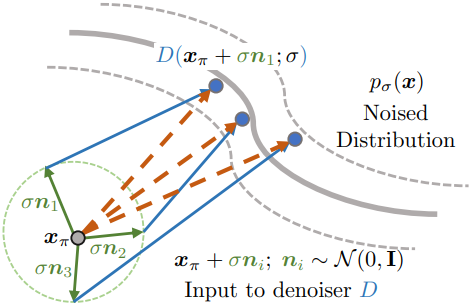
OOD 문제를 해결하기 위해, 본 논문은 Perturb-and-Average Scoring (PAAS)을 제안하였다. PAAS는 입력에 noise를 추가한 다음, 랜덤 noise에 대한 예측 score의 기대값으로 noise가 없는 이미지 $x_\pi$에 대한 score를 계산한다.

\[\begin{aligned} \textrm{PAAS} (x_\pi, \sqrt{2} \sigma) &:= \mathbb{E}_{n \sim \mathcal{N}(0,I)} [\textrm{score} (x_\pi + \sigma n, \sigma)] \\ &= \mathbb{E}_n \bigg[ \frac{D (x_\pi + \sigma n, \sigma) - (x_\pi + \sigma n)}{\sigma^2} \bigg] \\ &= \mathbb{E}_n \bigg[ \frac{D (x_\pi + \sigma n, \sigma) - x_\pi}{\sigma^2} \bigg] - \mathbb{E}_n \bigg[ \frac{n}{\sigma} \bigg] \\ &= \mathbb{E}_n \bigg[ \frac{D (x_\pi + \sigma n, \sigma) - x_\pi}{\sigma^2} \bigg] \end{aligned}\]

실제로는 기대값에 대한 몬테카를로 추정을 사용한다. 이 알고리즘은 위 그림에 설명되어 있다. 샘플링된 noise 집합 \(\{n_i\}\)이 주어지면 각 $D(x_\pi + \sigma n_i)$는 $x_\pi + \sigma n_i$에 대한 업데이트 방향을 제공한다. \(\{n_i\}\)에 대한 평균을 내어 $x_\pi$ 자체에 대한 업데이트 방향을 얻는다.

수학적 정당화

PAAS가 noise level $\sqrt{2} \sigma$에서 $x_\pi$의 score에 대한 근사값을 제공한다는 것을 보일 수 있다.

\[\begin{equation} \textrm{PAAS} (x_\pi, \sqrt{2} \sigma) \approx \nabla_{x_\pi} \log p_{\sqrt{2} \sigma} (x_\pi) \end{equation}\]

Proof. 두 Gaussian의 convolution은 Gaussian이며, 그 분산은 원래 두 Gaussian의 분산들의 합이다. 따라서 다음 식이 성립한다.

\[\begin{equation} \mathbb{E}_{n \sim \mathcal{N}(0,I)} [\mathcal{N}(x + \sigma n; \mu, \sigma^2 I)] = \mathcal{N} (x; \mu, 2 \sigma^2 I) \end{equation}\]

$p_\sigma (x)$는 mixture of Gaussians 형태이므로

\[\begin{aligned} p_{\sqrt{2} \sigma} (x_\pi) &= \mathbb{E}_{y \sim p_\textrm{data}} \mathcal{N} (x_\pi; y, 2 \sigma^2 I) \\ &= \mathbb{E}_{y \sim p_\textrm{data}} \mathbb{E}_{n \sim \mathcal{N}(0,I)} \mathcal{N} (x_\pi + \sigma n; y, \sigma^2 I) \\ &= \mathbb{E}_{n \sim \mathcal{N}(0,I)} \mathbb{E}_{y \sim p_\textrm{data}} \mathcal{N} (x_\pi + \sigma n; y, \sigma^2 I) \\ &= \mathbb{E}_{n \sim \mathcal{N}(0,I)} p_\sigma (x_\pi + \sigma n) \end{aligned}\]

이고, 양변에 로그를 취하고 Jensen’s inequality를 적용하면 다음과 같다.

\[\begin{aligned} \log p_{\sqrt{2} \sigma} (x_\pi) &= \log \mathbb{E}_{n \sim \mathcal{N}(0,I)} p_\sigma (x_\pi + \sigma n) \\ &\ge \mathbb{E}_{n \sim \mathcal{N}(0,I)} \log p_\sigma (x_\pi + \sigma n) \end{aligned}\]

양변에 gradient를 취하고 정리하면 다음과 같다.

\[\begin{aligned} \nabla_{x_\pi} \log p_{\sqrt{2} \sigma} (x_\pi) &\ge \nabla_{x_\pi} \mathbb{E}_{n \sim \mathcal{N}(0,I)} \log p_\sigma (x_\pi + \sigma n) \\ &= \mathbb{E}_{n \sim \mathcal{N}(0,I)} \nabla_{x_\pi + \sigma n} \log p_\sigma (x_\pi + \sigma n) \\ &= \mathbb{E}_{n \sim \mathcal{N}(0,I)} [\textrm{score}(x_\pi + \sigma n, \sigma)] \\ &= \textrm{PAAS} (x_\pi, \sqrt{2} \sigma) \end{aligned}\]

따라서, PAAS는 $x_\pi$에 대한 score의 하한이므로 근사값으로 사용할 수 있다.

2. Inverse Rendering on Voxel Radiance Field

2D score 계산이 해결되면 미분 가능한 renderer의 Jacobian에 대한 액세스가 필요하다.

3D 표현

3D 에셋 $\theta$를 voxel radiance field로 표현하는데, 이는 NeRF에 비해 접근 및 업데이트가 훨씬 빠르다. 파라미터 $\theta$는 density voxel grid \(V^\textrm{(density)} \in \mathbb{R}^{1 \times N_x \times N_y \times N_z}\)와 RGB voxel grid \(V^\textrm{(app)} \in \mathbb{R}^{3 \times N_x \times N_y \times N_z}\)로 구성된다. 단순화를 위해 뷰에 따른 효과를 모델링하지 않는다.

Inverse Volumetric Rendering

이미지 렌더링은 각 픽셀을 통과하는 카메라 광선을 따라 독립적으로 수행된다. 카메라 광선을 길이 $d$의 세그먼트로 자르고 $i$번째 세그먼트의 시작에 해당하는 공간 위치에서 trilinear interpolation을 사용하여 두 voxel grid에서 \((\textrm{RGB}_i, \tau_i)\)을 샘플링한다. 이러한 값은 다음과 같이 알파 블렌딩된다.

\[\begin{equation} C = \sum_i w_i \cdot \textrm{RGB}_i \\ \textrm{where} \; w_i = \alpha_i \cdot \prod_{j=0}^{i-1} (1 - \alpha_j), \; \alpha_i = 1 - \exp (-\tau_i d) \end{equation}\]

$\theta$의 볼륨 렌더링은 직접 미분 가능하다. 렌더링된 이미지 $x_\pi$에서 $\textrm{PAAS}(x_\pi)$와 Jacobian $J_\pi = \frac{\partial x_\pi}{\partial \theta}$ 사이의 Vector-Jacobian product는 score를 역전파하여 계산된다. 이 Vector-Jacobian product는 radiance field에서의 생성 모델링에 필요한 3D gradient를 제공한다.

정규화 전략

Voxel grid는 볼륨 렌더링을 위한 매우 강력한 3D 표현이다. 노이즈가 많은 2D guidance가 주어지면, 모델은 전체 그리드를 작은 밀도로 채워서 한 뷰에 대한 결합된 효과가 그럴듯하도록 속일 수 있다. 저자들은 일관된 3D 구조의 형성을 촉진하기 위한 몇 가지 기술을 제안하였다.

Emptiness Loss: 이상적으로, 공간은 물체를 제외하고는 거의 0의 밀도를 가져야 한다. 저자들은 광선 $r$에서 sparsity를 장려하기 위해 emptiness loss를 제안하였다.

\[\begin{equation} \mathcal{L}_\textrm{emptiness} (r) = \frac{1}{N} \sum_{i=1}^N \log (1 + \beta \cdot w_i) \end{equation}\]

로그 함수는 작은 가중치에서 큰 페널티를 부과하지만 가중치가 크면 급격하게 증가하지 않는다. 이는 낮은 밀도를 제거하기 위함이다. Hyperparameter $\beta$는 0에 가까운 loss function의 경사도를 제어한다. 큰 $\beta$는 낮은 밀도의 noise를 제거하는 데 더 많은 중점을 둔다.

논문에서는 $\beta = 10$으로 설정하였다.

Emptiness Loss Schedule: Emptiness loss의 기여도를 제어하기 위해 hyperparameter $\lambda$를 사용한다. 큰 emptiness loss를 적용하면 학습 초기 단계에서 형상 학습을 방해한다. 그러나 emptiness loss가 너무 작으면 floater 아티팩트가 발생한다. 이 문제를 해결하기 위해 2단계 노이즈 제거 스케줄을 채택하였다. 처음 $K$ iteration에서는 비교적 작은 가중치 $\lambda_1$을 사용하고, $K$번째 iteration 후에는 더 큰 \(\lambda_2\)로 증가시킨다.

논문에서는 \(\lambda_1 = 1 \times 10^4\), \(\lambda_1 = 2 \times 10^5\)로 설정하였다.

Center Depth Loss: 때때로 최적화는 물체를 장면 중심에서 멀리 배치한다. 물체는 작아지거나 이미지 경계 주변을 돌아다닌다. 이런 일이 발생하는 몇 가지 경우에 center depth loss를 적용한다.

\[\begin{equation} \mathcal{L}_\textrm{center} (D) = - \log \bigg( \frac{1}{\vert \mathcal{B} \vert} \sum_{p \in \mathcal{B}} D(p) - \frac{1}{\vert \mathcal{B}^c \vert} \sum_{q \notin \mathcal{B}} D(q) \bigg) \end{equation}\]

($D$는 깊이 이미지, $\mathcal{B}$는 이미지 중앙의 박스 (픽셀 위치의 집합))

Experiments

1. Validating PAAS on 2D images

다음은 FFHQ와 LSUN으로 각각 사전 학습된 DDPM과 Stable Diffusion에 대하여 PAAS로 2D 이미지를 샘플링한 예시들이다.

2. 3D Generation

다음은 사전 학습된 Stable Diffusion과 SJC를 활용하여 생성한 결과들이다.

다음은 Stable-DreamFusion과의 비교 결과이다.

3. Ablations

다음은 $\lambda$에 대한 ablation 결과이다.