[논문리뷰] SimPO: Simple Preference Optimization with a Reference-Free Reward
NeurIPS 2024 (Spotlight). [Paper] [Github]
Yu Meng, Mengzhou Xia, Danqi Chen
University of Virginia | Princeton University
23 May 2024

Introduction
인간의 피드백을 통한 학습은 LLM을 인간의 가치와 의도에 맞춰 조정하고, 유용하고 정직하며 무해하도록 보장하는 데 매우 중요하다. RLHF는 효과적인 정렬을 달성하기 위해 언어 모델을 fine-tuning하는 데 널리 사용되는 방법이다. 기존의 RLHF 방식은 인상적인 결과를 보여주었지만, reward 모델을 학습시킨 후 해당 reward를 극대화하기 위해 policy 모델을 최적화하는 다단계 절차로 인해 최적화에 어려움을 겪는다.
Direct Preference Optimization (DPO)는 RLHF의 reward function을 reparameterize하여 선호도 데이터로부터 policy 모델을 직접 학습시킴으로써 명시적인 reward 모델이 필요 없으며, 단순성과 안정성 덕분에 널리 채택되고 있다. DPO에서 reward는 현재 policy 모델과 SFT 모델 간의 응답 likelihood의 로그 비율을 사용하여 계산된다. 그러나 이 reward는 생성을 가이드하는 metric, 즉 policy 모델에서 생성된 응답의 평균 log likelihood과 직접적으로 일치하지 않는다. 학습과 inference 간의 이러한 불일치가 최적이 아닌 성능으로 이어질 수 있다.
본 논문에서는 간단하면서도 효과적인 오프라인 선호도 최적화 알고리즘인 SimPO를 제안하였다. 본 알고리즘의 핵심은 선호도 최적화 objective의 reward function을 생성 metric과 일치시키는 것이다. SimPO는 두 가지 주요 구성 요소로 구성된다.
- 길이 정규화된 reward: Policy 모델의 응답에 포함된 모든 토큰의 평균 log probability
- target reward margin: 승리 응답과 패배 응답 간의 reward 차이가 초과해야 하는 값
요약하면, SimPO는 다음과 같은 특성을 갖는다.
- 단순성: SimPO는 레퍼런스 모델이 필요하지 않아 DPO나 기타 레퍼런스 기반 방법에 비해 가볍고 구현이 쉽다.
- 상당한 성능 이점: SimPO는 DPO보다 훨씬 우수한 성능을 보인다.
- Minimal length exploitation: SimPO는 SFT 또는 DPO 모델에 비해 응답 길이를 크게 증가시키지 않는다.
Method
1. Background: Direct Preference Optimization (DPO)
DPO는 가장 널리 사용되는 선호도 최적화 방법 중 하나이다. DPO는 명시적인 reward 모델을 학습하는 대신, closed-form 표현식을 사용하여 reward function $r$을 reparameterize한다.
\[\begin{equation} r(x,y) = \beta \log \frac{\pi_\theta (y \vert x)}{\pi_\textrm{ref} (y \vert x)} + \beta \log Z(x) \end{equation}\](\(\pi_\theta\)는 policy 모델, \(\pi_\textrm{ref}\)는 레퍼런스 policy (일반적으로 SFT 모델), $Z(x)$는 partition function)
이 reward를 Bradley-Terry (BT) ranking objective에 통합함으로써, DPO는 reward 모델이 아닌 policy 모델을 사용하여 선호도 데이터의 확률을 표현하며, 다음과 같은 objective를 사용한다.
\[\begin{equation} \mathcal{L}_\textrm{DPO} (\pi_\theta; \pi_\textrm{ref}) = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \left[ \log \sigma \left( \beta \log \frac{\pi_\theta (y_w \vert x)}{\pi_\textrm{ref} (y_w \vert x)} - \beta \log \frac{\pi_\theta (y_l \vert x)}{\pi_\textrm{ref} (y_l \vert x)} \right) \right] \end{equation}\](\((x, y_w, y_l)\)은 선호도 데이터셋 $\mathcal{D}$의 프롬프트, 승리하는 응답, 패배하는 응답으로 구성된 선호도 쌍)
2. A Simple Reference-Free Reward Aligned with Generation
DPO에 대한 reward와 생성 간의 불일치
위의 $r(x,y)$를 implicit reward로 사용하면 다음과 같은 단점이 있다.
- 학습 중에 레퍼런스 모델 \(\pi_\textrm{ref}\)가 필요하므로 추가 메모리와 계산 비용이 발생한다.
- 학습에서 최적화된 reward와 inference 중에 최적화된 log-likelihood 간에 불일치가 발생한다. 즉, DPO에서 모든 $(x, y_w, y_l)$에 대해 $r(x, y_w) > r(x, y_l)$을 충족하는 것이 반드시 \(p_\theta (y_w \vert x) > p_\theta (y_l \vert x)\)를 충족한다는 것을 의미하지는 않는다 (\(p_\theta\)는 평균 log-likelihood). DPO로 학습했을 때 학습 세트의 약 50%만이 이 조건을 충족한다.
길이로 정규화된 reward 공식
한 가지 해결책은 합산된 토큰 log probability를 reward로 사용하는 것이지만, 시퀀스가 길수록 log probability가 낮아지는 경향이 있기 때문에 이 방법은 길이 편향이 발생한다. 결과적으로 합산된 log probability를 reward로 최적화하면, $y_w$가 $y_l$보다 길 때 모델은 $y_w$가 $y_l$보다 더 높은 reward를 받도록 하기 위해 더 긴 시퀀스에 대한 확률을 인위적으로 부풀리게 된다.
이 문제를 해결하기 위해 평균 log-likelihood를 implicit reward로 사용하는 것을 고려해 보자.
\[\begin{equation} p_\theta (y \vert x) = \frac{1}{\vert y \vert} \log \pi_\theta (y \vert x) = \frac{1}{\vert y \vert} \sum_{i=1}^{\vert y \vert} \log \pi_\theta (y_i \vert x, y_{<i}) \end{equation}\]이 metric은 beam search나 객관식 문제에서 순위를 매기는 데 일반적으로 사용된다. DPO의 reward를 위 식의 \(p_\theta\)로 대체하여 생성을 가이드하는 likelihood metric과 일치하도록 하면, 길이 정규화된 reward는 다음과 같다.
\[\begin{equation} r_\textrm{SimPO}(x, y) = \frac{\beta}{\vert y \vert} \log \pi_\theta (y \vert x) = \frac{\beta}{\vert y \vert} \sum_{i=1}^{\vert y \vert} \log \pi_\theta (y_i \vert x, y_{<i}) \end{equation}\]($\beta$는 reward 차이의 scaling을 제어하는 상수)
Reward를 응답 길이로 정규화하는 것은 매우 중요하다. Reward에서 길이 정규화 항을 제거하면 더 길지만 품질이 낮은 시퀀스를 생성하는 경향이 있다. 결과적으로, 이 reward는 레퍼런스 모델의 필요성을 없애 레퍼런스 모델에 의존하는 알고리즘에 비해 메모리와 계산 효율을 향상시킨다.
3. The SimPO Objective
Target reward margin
또한, 승리 응답에 대한 reward $r(x, y_w)$가 패배 응답에 대한 reward $r(x, y_l)$보다 최소 $\gamma$만큼 더 크도록 보장하기 위해 Bradley-Terry objective에 target reward margin 항 $\gamma > 0$을 도입한다.
\[\begin{equation} p (y_w \succ y_l \vert x) = \sigma (r(x, y_w) - r (x, y_l) - \gamma) \end{equation}\]두 클래스 간의 마진은 classifier의 일반화 성능에 긍정적인 영향을 미친다. 선호도 최적화에서는 두 클래스가 하나의 입력에 대해 승패를 가르는 응답이 된다. 실제로, $\gamma$가 증가함에 따라 생성 품질이 처음에는 향상되지만 $\gamma$가 너무 커지면 생성 품질이 저하된다.
Objective
\(r_\textrm{SimPO}(x, y)\)를 위 식에 대입하여 SimPO objective를 얻을 수 있다.
\[\begin{equation} \mathcal{L}_\textrm{SimPO} (\pi_\theta) = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \left[ \log \sigma \left( \frac{\beta}{\vert y_w \vert} \log \pi_\theta (y_w \vert x) - \frac{\beta}{\vert y_l \vert} \log \pi_\theta (y_l \vert x) - \gamma \right) \right] \end{equation}\]KL regularization 없이 catastrophic forgetting 방지
SimPO는 KL regularization을 적용하지 않지만, 다음과 같은 요인들의 조합이 일반화를 유지하면서 선호도 데이터로부터 효과적인 학습을 보장하여 레퍼런스 모델과의 낮은 KL divergence를 유도한다.
- 낮은 learning rate
- 다양한 도메인과 task를 포괄하는 선호도 데이터셋
- 기존 지식을 잃지 않고 새로운 데이터로부터 학습하는 LLM의 고유한 robustness
Experiments
1. Main Results and Ablations
다음은 다양한 선호도 최적화 방법들과 성능을 비교한 결과이다.
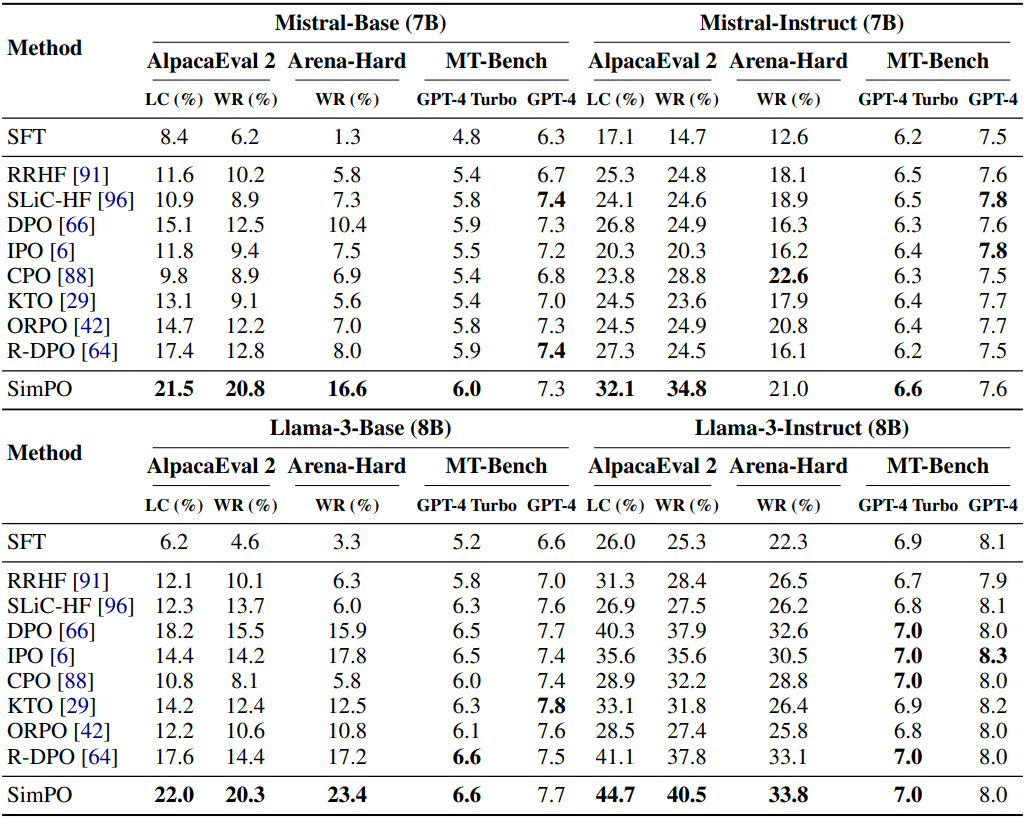
다음은 ablation 결과이다.
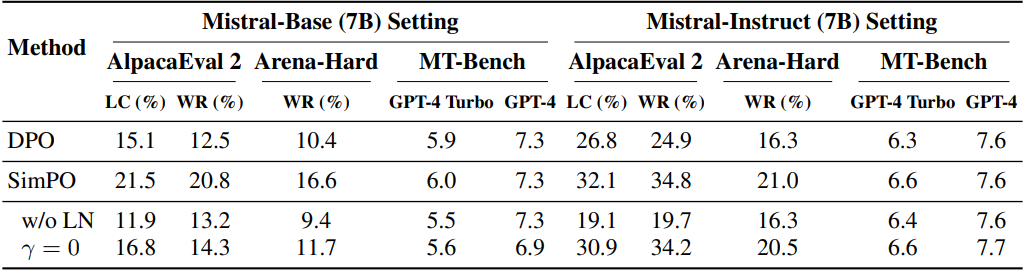
2. Length Normalization (LN) Prevents Length Exploitation
다음은 길이 정규화의 영향을 나타낸 그래프들이다.
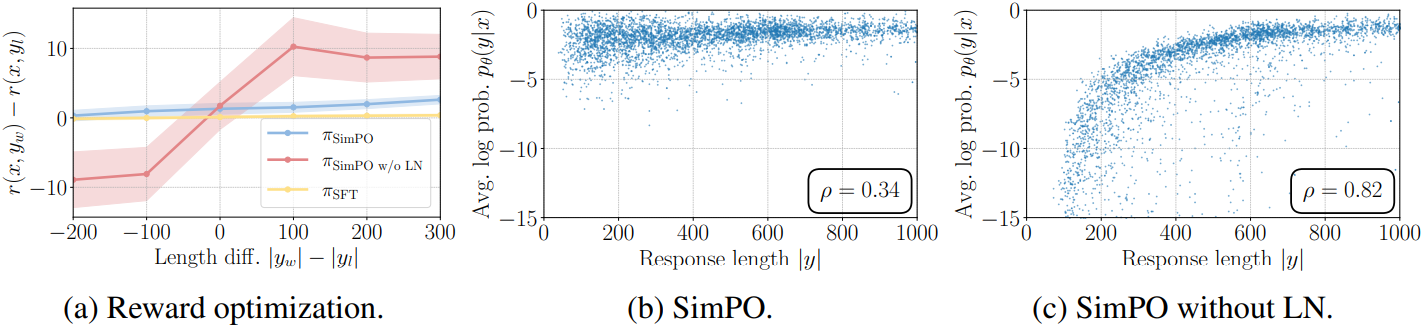
길이 정규화 없이 학습된 모델은 SimPO 모델에 비해 likelihood와 응답 길이 사이에 훨씬 더 강한 양의 상관관계를 보이는데, 이는 길이 편향을 이용하여 더 긴 시퀀스를 생성하는 경향을 나타낸다. 반면, SimPO 모델은 SFT 모델과 유사한 상관관계 계수를 나타낸다.
3. The Impact of Target Reward Margin in SimPO
다음은 target reward margin $\gamma$에 대한 영향을 나타낸 그래프들이다.
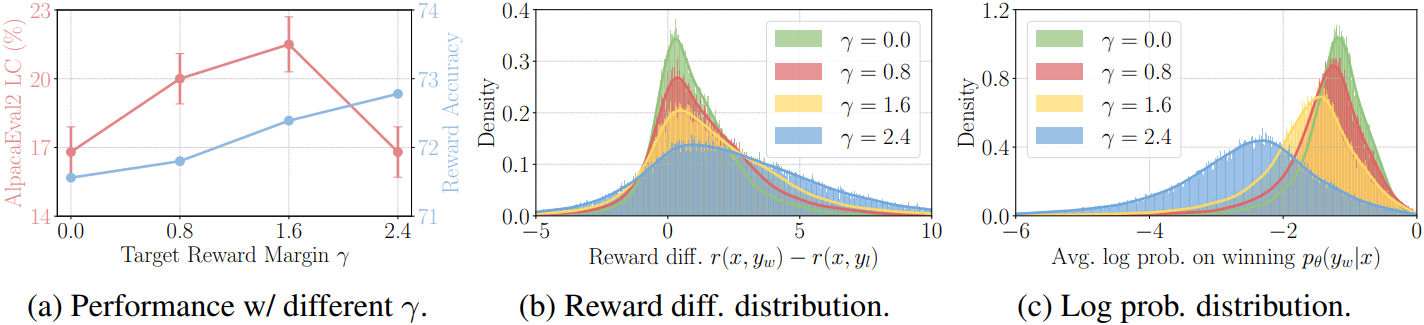
Reward 정확도는 $\gamma$에 따라 증가하였지만, AlpacaEval 2에서의 승률은 $\gamma$에 따라 먼저 증가하다가 감소하는데, 이는 생성 품질이 reward margin만으로 결정되는 것이 아님을 시사한다. 또한, $\gamma$ 값을 증가시키면 승리 응답과 패배 응답 사이의 reward 차이의 분포와 승리 응답에 대한 log probability 분포가 모두 평탄해지고, 승리 응답의 평균 log likelihood가 감소하는 경향이 있다. 이는 초기에는 성능을 향상시키지만, 결국에는 모델이 악화될 수 있다.
$\gamma$ 값을 설정할 때 실제 reward 분포를 정확하게 근사하는 것과 잘 보정된 likelihood를 유지하는 것 사이에 상충 관계가 있다.
4. In-Depth Analysis of DPO vs. SimPO
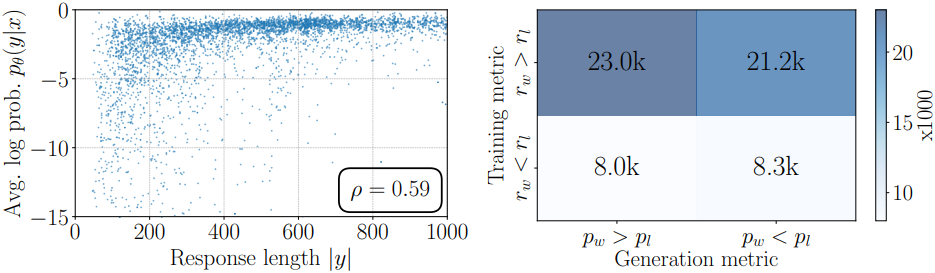
다음은 평균 log likelihood와 응답 길이 사이의 스피어만 상관계수 $\rho$를 비교한 결과이다.

다음은 DPO의 (왼쪽) 응답 길이에 따른 평균 log probability와 (오른쪽) reward와 log likelihood 사이의 관계를 분석한 결과이다.
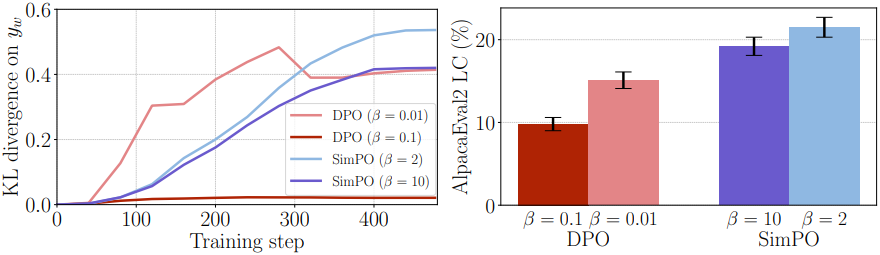
다음은 $\beta$에 따른 KL divergence와 성능을 비교한 결과이다.
다음은 DPO와 SimPO의 메모리 및 컴퓨팅 효율성을 비교한 결과이다.