[논문리뷰] simple diffusion: End-to-end diffusion for high resolution images
arXiv 2023. [Paper]
Emiel Hoogeboom, Jonathan Heek, Tim Salimans
Google Research, Brain Team
26 Jan 2023

Introduction
Diffusion model은 이미지, 오디오, 비디오 생성에 매우 효과적인 것으로 나타났다. 그러나 높은 해상도에 대해서 논문들은 일반적으로 낮은 차원의 잠재 공간에서 작동하거나 여러 하위 문제로 나눈다. 이러한 접근 방식의 단점은 추가 복잡성을 유발하고 일반적으로 단일 end-to-end 학습 설정을 지원하지 않는다는 것이다.
본 논문에서는 모델을 가능한 한 단순하게 유지하면서 더 높은 해상도를 위해 표준 denoising diffusion을 개선하는 것을 목표로 한다. 본 논문의 네 가지 주요 발견은 다음과 같다.
- 해상도가 증가함에 따라 더 많은 noise를 추가하여 더 큰 이미지에 대해 noise schedule을 조정해야 한다.
- 성능 향상을 위해 U-Net 아키텍처를 16$\times$16 해상도로 확장하는 것으로 충분하다. 한 단계 더 나아가면 Transformer backbone이 있는 U-Net인 U-ViT 아키텍처가 있다.
- 성능 향상을 위해 dropout을 추가해야 하지만 최고 해상도의 feature map에는 추가하지 않는다.
- 더 높은 해상도를 위해 성능 저하 없이 downsampling할 수 있다.
가장 중요한 것은 이러한 결과가 단 하나의 모델과 end-to-end 학습 설정을 사용하여 얻은 것이라는 점이다. 기존 distillation 테크닉을 사용하면 단일 step에만 적용하면 되므로 모델은 0.4초 안에 이미지를 생성할 수 있다.
Method: simple diffusion
1. Adjusting Noise Schedules
수정 사항 중 하나는 일반적으로 diffusion model에 사용되는 noise schedule이다. 가장 일반적인 schedule은 variance preserving 가정 하에서 $\sigma_t / \alpha_t = \tan ( \pi / 2 )$에 해당하는 $\alpha$-cosine schedule이다. 이 schedule은 원래 해상도가 32$\times$32인 CIFAR-10과 ImageNet 64$\times$64의 성능을 개선하기 위해 제안되었다.

그러나 고해상도의 경우 충분한 noise가 추가되지 않는다. 예를 들어, 위 그림의 맨 위 행을 살펴보면 표준 cosine schedule의 경우 이미지의 전체 구조가 이미 넓은 범위의 시간에 대해 대체로 정의되어 있음을 알 수 있다. 이는 생성적 denoising process가 이미지의 전체 구조를 결정할 수 있는 작은 time window만 있기 때문에 문제가 된다. 더 높은 해상도의 경우 이 schedule을 예측 가능한 방식으로 변경하여 우수한 시각적 샘플 품질을 유지할 수 있다.
저자들은 이러한 필요성을 더 자세히 설명하기 위해 128$\times$128 문제를 연구하였다. 입력 이미지 $x$가 주어지면 픽셀 $i$에 대한 diffusion 분포는
\[\begin{equation} q(z_t^{(i)} \vert x) = \mathcal{N} (z_t^{(i)} \vert \alpha_t x_i, \sigma_t) \end{equation}\]로 지정된다. 일반적으로 diffusion model은 downsampling을 사용하여 저해상도 feature map에서 작동하는 아키텍처를 사용한다. 이 경우에는 average pooling을 사용한다. $z_t$에 2$\times$2 average pooling을 한다고 하면 새 픽셀은
\[\begin{equation} z_t^{64 \times 64} = \frac{z_t^{(1)} + z_t^{(2)} + z_t^{(3)} + z_t^{(4)}}{4} \end{equation}\]이다. 독립 확률 변수의 분산은 다음과 같은 특성을 가지고 있다.
\[\begin{equation} \textrm{Var}[X_1 + X_2] = \textrm{Var}[X_1] + \textrm{Var}[X_1] \\ \textrm{Var}[aX] = a^2 \textrm{Var}[X_1] \end{equation}\]따라서 $x^{64 \times 64}$를 average pooling된 입력 이미지의 첫 번째 픽셀이라고 하면
\[\begin{equation} z_t^{64 \times 64} \sim \mathcal{N} (\alpha_t x^{64 \times 64}, \sigma_t / 2) \end{equation}\]임을 알 수 있다. 즉, 저해상도 픽셀 $z_t^{64 \times 64}$는 noise 양이 절반만 있다. 저자들은 해상도가 증가함에 따라 전체 일관성이 생성되는 단계인 낮은 해상도에서 훨씬 적은 diffusion time이 소요되기 때문에 문제가 있다고 가정한다.
더 낮은 해상도에서 $\alpha_t$-to-$\sigma_t$ 비율이 두 배로 높다는 것을 유도할 수 있다. 즉, SNR이 $2^2$만큼 높다는 의미이다. 일반화하면 다음과 같다.
\[\begin{equation} \textrm{SNR}^{d/s \times d/s} (t) = \textrm{SNR}^{d \times d} (t) \cdot s^2 \end{equation}\]정리하면, window 크기 $s \times s$로 average pooling을 하면 $\alpha_t$-to-$\sigma_t$ 비율이 $s$배 높아지고 SNR이 $s^2$배 높아진다. 따라서 저자들은 noise schedule이 성공적으로 테스트된 reference 해상도를 기준으로 정의되어야 한다고 주장한다.
저자들은 실험적으로 64$\times$64를 reference 해상도로 설정하였다. Reference 해상도와 $d \times d$ 해상도에서의 SNR은 다음과 같이 정의된다.
\[\begin{equation} \textrm{SNR}^{64 \times 64} (t) = 1 / \tan(\pi t / 2)^2 \\ \textrm{SNR}_\textrm{shift 64}^{d \times d} (t) = \textrm{SNR}^{64 \times 64} (t) \cdot (64 / d)^2 \end{equation}\]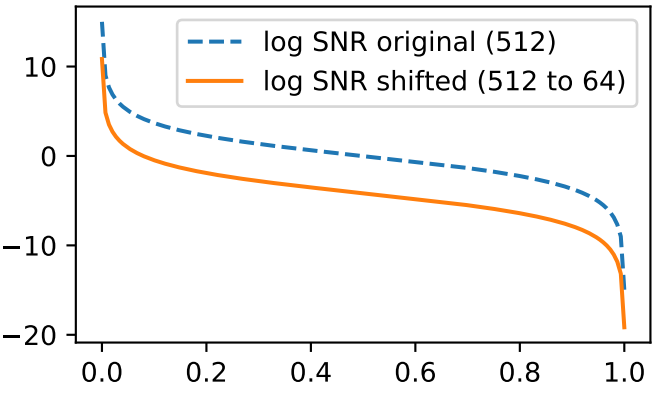
Log-space에서는 위 그래프와 같이 간단히 $2 \cdot \log (64/d)$만큼 shift하는 것과 같다. Variance preserving process 하에서는 diffusion parameter가 다음과 같이 계산된다.
Interpolating schedules
Shift schedule의 잠재적인 단점은 증가된 픽셀당 noise로 인해 diffusion process에서 훨씬 나중에 고주파수 디테일이 생성된다는 것이다. 그러나 이미 생성된 전역/저주파수 feature로 컨디셔닝할 때 고주파수 디테일이 약하게 상관된다고 가정한다. 따라서 몇 번의 diffusion step에서 고주파수 디테일을 생성하는 것이 가능해야 한다. 또는 다른 shift schedule을 보간할 수 있다. 예를 들어 해상도 512의 경우 shift 32에서 시작하여 로그 공간에서 shift 256으로 보간하여 더 높은 주파수의 디테일을 포함할 수 있다.
\[\begin{equation} \log \textrm{SNR}_{\textrm{interpolate}(32 \rightarrow 256)} (t) = t \log \textrm{SNR}_\textrm{shift 256}^{512 \times 512} (t) + (1-t) \log \textrm{SNR}_\textrm{shift 32}^{512 \times 512} (t) \end{equation}\]이렇게 하면 각 주파수 디테일에 대해 더 동일한 가중치를 갖는다.
2. Multiscale training loss
앞서 기본 해상도에서 SNR이 일정하게 유지되도록 고해상도 이미지를 학습할 때 diffusion model의 noise schedule을 조정해야 한다고 했다. 그러나 이러한 방식으로 noise schedule을 조정하더라도 해상도가 점점 높아지는 이미지의 학습 loss은 고주파수 디테일에 의해 지배된다. 이를 수정하기 위해 downsampling된 해상도에서 표준 학습 loss를 평가하는 multiscale loss로 표준 학습 loss를 대체하고 더 낮은 해상도에 대해 증가하는 가중 요소를 제안한다. 저자들은 multiscale loss가 특히 256$\times$256보다 큰 해상도에서 더 빠른 수렴을 가능하게 한다는 것을 발견했다. $d \times d$ 해상도에서의 학습 loss는 다음과 같이 쓸 수 있다.
\[\begin{equation} L_\theta^{d \times d} (x) = \frac{1}{d^2} \mathbb{E}_{\epsilon, t} \| D^{d \times d} [\epsilon] - D^{d \times d} [\hat{\epsilon}_\theta (\alpha_t x + \sigma_t \epsilon, t)] \|_2^2 \end{equation}\]$D^{d \times d}$는 $d \times d$ 해상도로 downsampling하는 것을 뜻한다. 이미지를 downsampling하는 것이 선형 연산이므로
\[\begin{equation} D^{d \times d} [\mathbb{E} (\epsilon \vert x)] = \mathbb{E} (D^{d \times d} [\epsilon] \vert x) \end{equation}\]이다. 따라서 저해상도 모델을 구성하는 이러한 방식은 원래 모델과 실제로 일치한다.
그런 다음 여러 해상도로 구성된 multiscale 학습 loss에 대한 고해상도 모델 학습을 한다. 예를 들어, 해상도 $32, 64, \cdots, d$에 대한 loss는 다음과 같다.
\[\begin{equation} \tilde{L}_\theta^{d \times d} (x) = \sum_{s \in \{32, 64, \cdots, d\}} \frac{1}{s} L_\theta^{s \times s} (x) \end{equation}\]즉, 기본 해상도(이 경우 32$\times$32)에서 시작하고 항상 $d \times d$의 최종 해상도를 포함하는 해상도에 대한 학습 loss의 가중 합에 대해 학습시킨다. 더 높은 해상도에 대한 loss는 평균적으로 노이즈가 더 많으므로 해상도를 높일수록 loss의 상대적 가중치를 줄인다.
3. Scaling the Architecture
또 다른 질문은 어떻게 아키텍처를 확장하는 지이다. 일반적인 모델 아키텍처는 해상도가 두 배가 될 때마다 채널이 절반이므로 연산당 flops는 동일하지만 feature의 수는 두 배가 된다. 계산 강도 (flops/features)도 해상도가 두 배가 될 때마다 절반으로 줄어든다. 계산 강도가 낮으면 가속기 사용률이 낮아지고 activation이 크면 메모리 부족 문제가 발생한다. 따라서 저해상도 feature map에서 확장하는 것을 선호한다. 저자들의 가설은 주로 특정 해상도, 즉 16$\times$16 해상도로 확장하면 저자들이 고려하는 네트워크 크기 범위 내에서 성능을 향상시키기에 충분하다. 일반적으로 저해상도 연산은 비교적 작은 feature map을 가진다.
다음 표는 $B = 1024$일 때의 convolutional kernel과 feature map의 일반적인 메모리 사용량을 나타낸 것이다.

중요한 점은 16$\times$16 해상도의 경우 feature map 크기와 parameter 메모리 모두 다루기 쉽다는 것이며, 전체 메모리 사용량이 23배 차이가 난다.
이 해상도를 선택하는 다른 이유는 많은 diffusion 논문의 연구에서 self-attention이 사용되기 시작했기 때문이다. 또한 classification을 위한 vision transformer가 성공적으로 작동할 수 있는 해상도도 16$\times$16 해상도다. 이것이 아키텍처를 확장하는 이상적인 방법이 아닐 수도 있지만 16$\times$16 확장이 경험적으로 잘 작동한다.
Avoiding high resolution feature maps
고해상도 feature map은 메모리 비용이 많이 든다. FLOP 수가 일정하게 유지되면 메모리는 여전히 해상도에 따라 선형적으로 확장된다. 실제로는 가속기 사용률을 희생하지 않고 특정 크기 이상으로 채널을 줄이는 것은 불가능하다. 최신 가속기는 컴퓨팅과 메모리 대역폭 간의 비율이 매우 높다. 따라서 채널 수가 적으면 연산 메모리가 제한되어 대부분 idling이 발생하고 예상 성능보다 나빠질 수 있다.
가장 높은 해상도에서 계산을 수행하는 것을 피하기 위해 신경망의 첫 번째 step으로 이미지를 즉시 downsampling하고 마지막 step으로 upsampling한다. 저자들은 놀랍게도 이 신경망이 계산 및 메모리 측면에서 더 저렴하지만 경험적으로 더 나은 성능을 달성한다는 사실을 발견했다고 한다. 선택할 수 있는 두 가지 접근 방식이 있다.

한 가지 접근 방식은 가역이고 선형적인 5/3 wavelet(JPEG2000에서 사용)을 사용하여 이미지를 위 그림과 같이 저해상도 frequency response으로 변환하는 것이다. 여기에서 다양한 feature response는 시각적 목적을 위해 공간적으로 연결된다. 네트워크에서 response는 채널 축을 통해 연결된다. 둘 이상의 DWT 레벨이 적용되는 경우 response의 해상도가 다르다. 이는 가장 낮은 해상도(그림에서 $128^2$)를 찾고 더 높은 해상도의 feature map을 위해 픽셀을 재구성함으로써 해결된다. $256^2$의 경우 일반적인 공간에서 깊이 연산으로 $128^2 \times 4$로 재구성된다.
위의 내용이 복잡해 보이고 약간의 성능 저하를 감수할 의향이 있다면 더 간단한 해결책도 있다. 첫 번째 layer로 stride가 $d$인 $d \times d$ convolutional layer을 사용할 수 있고 마지막 layer로 동일한 모양의 transposed convolutional layer을 사용할 수 있다. 이것은 transformer 논문에서 patching이라고 하는 것과 동일하다. 경험적으로 이것이 약간 더 나쁘긴 하지만 유사하게 수행된다.
4. Dropout
일반적으로 diffusion에 사용되는 아키텍처에서는 모든 해상도에서 residual block에 global dropout hyperparameter가 사용된다. CDM에서 dropout은 낮은 해상도에서 이미지를 생성하는 데 사용된다. 조건부 고해상도 이미지의 경우 dropout이 사용되지 않는다. 그러나 다양한 다른 형태의 augmentation이 데이터에 대해 수행된다. 이는 고해상도에서 작동하는 모델의 경우에도 정규화가 중요함을 나타낸다. 그러나 경험적으로 모든 residual block에 dropout을 추가하는 naive한 방법은 원하는 결과를 제공하지 않는다.
본 논문의 네트워크 디자인은 낮은 해상도에서만 네트워크 크기를 확장하기 때문에 저자들은 dropout만 추가하고 낮은 해상도를 추가하는 것으로 충분해야 한다는 가설을 세운다. 이렇게 하면 메모리 비용이 많이 드는 고해상도 layer를 정규화하는 것을 피하면서 저해상도 이미지에서 학습된 모델에 성공한 dropout regularization을 계속 사용한다.
5. The U-ViT architecture
아키텍처에 대한 위에서 설명한 변경 사항을 한 단계 더 살펴보면 아키텍처가 이미 해당 해상도에서 self-attention을 사용하는 경우 convolutional layer를 MLP 블록으로 대체할 수 있다. 이것은 Scalable diffusion models with transformers 논문에서 도입된 diffusion용 transformer를 U-Nets와 연결하여 backbone을 transformer로 대체한다. 결과적으로 이 상대적으로 작은 변화는 이제 이러한 해상도에서 transformer block을 사용하고 있음을 의미한다. 주요 이점은 self-attention과 MLP 블록의 조합이 가속기 사용률이 높기 때문에 큰 모델이 다소 빠르게 학습된다는 것이다. 본질적으로 이 U-Vision Transformer(U-ViT) 아키텍처는 여러 레벨을 통해 16$\times$16 해상도로 downsampling하는 작은 convolutional U-Net으로 볼 수 있다. 여기에 대형 transformer가 적용된다. 그런 다음 convolutional U-Net을 통해 upsampling이 다시 수행된다.
6. Text to image generation
저자들은 개념 증명을 위해 텍스트 데이터를 기반으로 하는 간단한 diffusion model도 학습시킨다. 저자들은 T5 XXL 텍스트 인코더를 컨디셔닝으로 사용한다. 총 세 가지 모델을 학습시키며 각각 해상도가 256$\times$256, 512$\times$512, 384$\times$640이다.
Experiments
1. Effects of the proposed modifications
Noise schedule
다음은 ImageNet 128$\times$128과 256$\times$256에서 noise schedule에 따른 FID를 측정한 표이다.
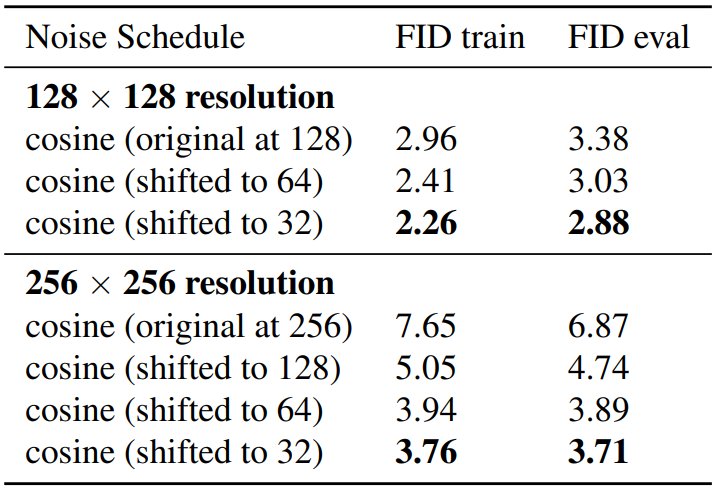
Noise schedule을 shifting하는 것이 상당히 성능을 개선하는 것을 볼 수 있다. 특히 더 높은 해상도에서 성능 개선 효과가 컸다.
Dropout
다음은 ImageNet 128$\times$128에서 dropout에 대한 ablation study 결과 표이다.
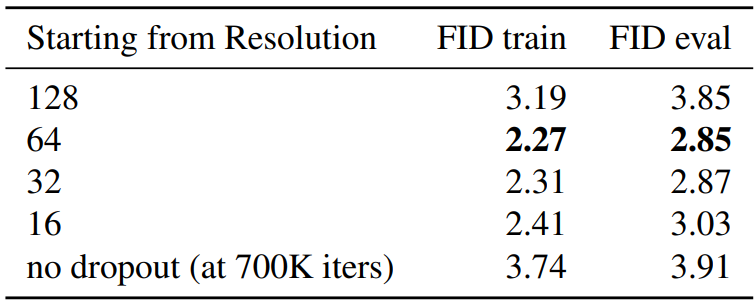
저자들은 낮은 해상도 feature map에서 작동하는 네트워크의 모듈을 정규화하기에 충분해야한다는 가설을 세웠으며, 이 가설이 만족하는 것을 알 수 있다. 데이터와 같은 크기의 해상도부터 dropout을 적용하는 경우 성능이 거의 개선되지 않았다. 이는 고해상도 diffusion에 대한 dropout이 지금까지 널리 사용되지 않은 이유를 설명 할 수 있다. 일반적으로 dropout은 모든 해상도에서 모든 feature map의 글로벌 파라미터로 설정되어 있지만 이 실험은 그러한 정규화가 너무 공격적이라는 것을 보여준다.
Architecture scaling
다음 표는 U-Net 아키텍처를 스케일링하였을 때의 성능을 비교한다.
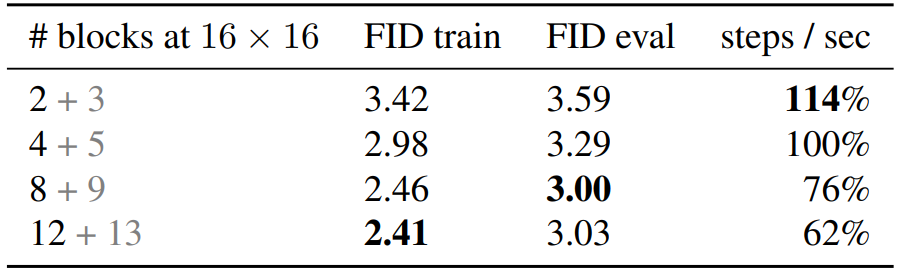
“2+3”은 2개의 down block과 3개의 up block으로 U-Net을 구성한다는 뜻이다. 모듈 개수를 늘리면 성능이 일반적으로 개선되지만 block 개수가 8에서 12로 증가하는 경우 성능 개선이 거의 없다.
Avoiding higher resolution feature maps
다음 표는 ImageNet 512$\times$512에서의 downsampling 전략에 따른 성능을 비교한 것이다.
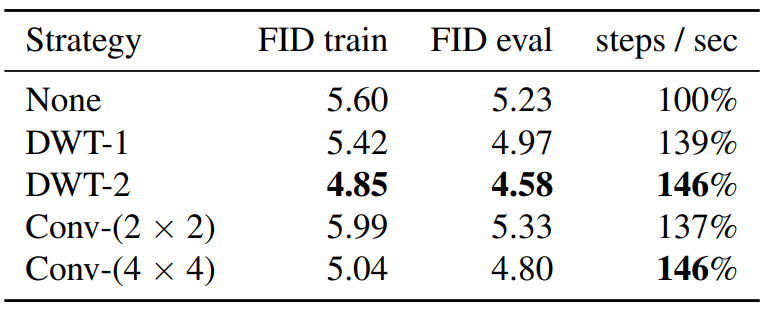
Multiscale loss
다음은 multiscale loss를 적용할 때의 성능을 비교한 것이다.
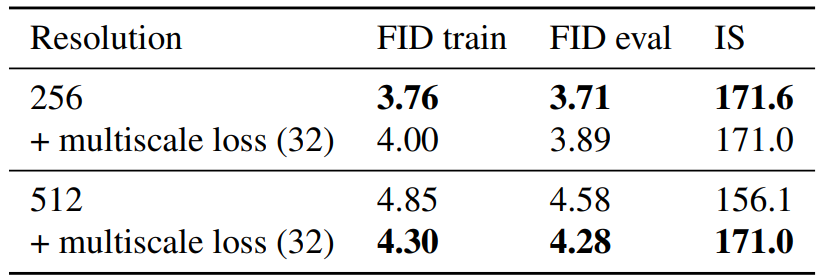
Multiscale loss는 높은 해상도에서는 효과적이지만 낮은 해상도에서는 성능이 약간 감소한다.
2. Comparison with literature
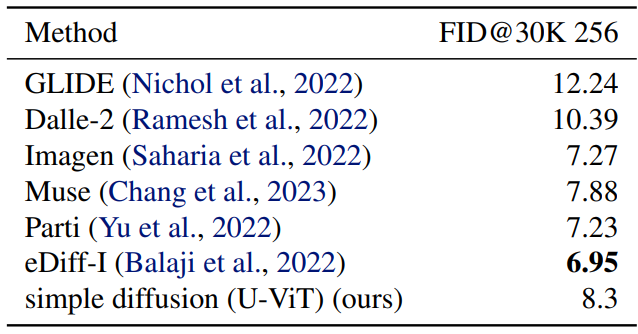
다음은 다른 논문들의 생성 모델들과 ImageNet에서 비교한 표이다.

다음은 simple diffusion으로 생성한 이미지이다. 각 이미지들은 cascades (super-resolution) 없이 하나의 diffusion model로 full image space에서 생성되었다. (guidance scale 4)

Text to image
다음은 zero-shot COCO에 대한 text to image 결과를 나타낸 표이다.
다음은 512$\times$512 해상도에서의 text to image 샘플들이다. 이 모델은 distillation을 사용한 것으로 이미지 1개를 생성하는 데 TPUv4에서 0.42초가 걸린다 (텍스트 인코더 제외).

다음은 256$\times$256 해상도에서의 text to image 샘플들이다.
