[논문리뷰] One Step Diffusion via Shortcut Models
ICLR 2025 (Oral). [Paper] [Page] [Github]
Kevin Frans, Danijar Hafner, Sergey Levine, Pieter Abbeel
UC Berkeley
16 Oct 2024

Introduction
본 논문은 한 번의 학습을 통해 one-step denoiser가 획득되는 end-to-end 설정을 고려하였다. 이전의 2단계 방법들은 이미 학습된 diffusion model을 추가로 one-step model로 distillation한다. 이는 복잡성을 도입하고 대규모 합성 데이터셋을 생성하거나 일련의 teacher 및 student 네트워크를 통해 전파해야 한다. Consistency model은 end-to-end에 한 걸음 더 가까워졌지만 대량의 부트스트래핑에 대한 의존성으로 인해 학습하는 동안 신중한 schedule이 필요하다. 이러한 방법들은 학습을 종료하고 distillation을 시작할 시기를 지정해야 한다. 반면에 end-to-end 방법은 지속적으로 성능을 개선하기 위해 무기한으로 학습시킬 수 있다.
본 논문은 이러한 end-to-end로 학습되는 one-step 생성 모델 클래스인 shortcut model을 제시하였다. 핵심 통찰력은 신경망을 noise level뿐만 아니라 원하는 step 크기로 컨디셔닝하여 denoising process에서 정확하게 앞으로 갈 수 있도록 하는 것이다. Shortcut model은 학습 시간 동안 자체 distillation을 수행하는 것으로 볼 수 있으므로 별도의 distillation 단계가 필요하지 않으며 한 번의 학습만이 필요하다. 또한 신중한 학습 schedule이나 warm-up이 필요하지 않다. Shortcut model은 학습이 효율적이며 기본 diffusion model보다 약 16% 더 많은 컴퓨팅만 필요하다.
Shortcut model은 few-step 및 one-step 설정에서 2단계 distillation 방법과 성능이 비슷하거나 더 나은 성능을 낼 수 있다.
Method
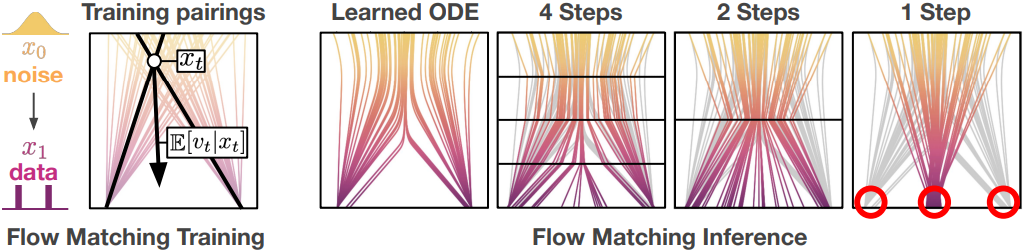
위 그림에서 볼 수 있듯이, flow-matching은 곡선 경로를 따라 noise를 데이터에 매핑하는 ODE를 학습한다. 단순하게 큰 샘플링 step을 취하면 큰 discretization error가 발생하고 step이 하나인 경우 치명적인 오차가 발생한다. $d$에 대한 컨디셔닝을 통해 shortcut model은 미래의 곡률을 고려하고 궤도를 벗어나지 않고 올바른 다음 지점으로 점프할 수 있다. $x_t$에서 올바른 다음 지점 $x_{t+d}^\prime$으로 향하는 정규화된 방향을 shortcut $s(x_t, t, d)$라고 한다.
본 논문의 목표는 $x_t$, $t$, $d$의 모든 조합에 대한 shortcut을 학습한 shortcut model $s_\theta (x_t, t, d)$를 학습시키는 것이다. 따라서 shortcut model은 더 큰 step 크기에 대한 flow-matching model의 일반화로 볼 수 있다. flow-matching model은 순간 속도만 학습하는 반면, shortcut model은 추가로 더 큰 점프를 하는 법을 학습한다. $d \rightarrow 0$이면 shortcut은 flow와 동등하다.
$s_\theta (x_t, t, d)$를 학습시키기 위한 target을 계산하는 단순한 방법은 충분히 작은 step 크기로 ODE forward를 완전히 시뮬레이션하는 것이다. 그러나 이 접근 방식은 특히 end-to-end 학습의 경우 계산 비용이 많이 든다. 대신, shortcut model의 고유한 자기 일관성 (self-consistency) 속성을 활용한다. 즉, 하나의 shortcut step은 크기가 절반인 두 개의 연속된 shortcut step과 같다.
\[\begin{equation} s(x_t, t, 2d) = \frac{s(x_t, t, d) + s(x_{t+d}^\prime, t, d)}{2} \end{equation}\]이를 통해 $d > 0$에 대해서는 self-consistency target을 사용하고 $d = 0$에 대해서는 flow-matching loss를 사용하여 shortcut model을 학습시킬 수 있다. 원칙적으로 임의의 $d$ 분포에서 모델을 학습시킬 수 있지만, 실제로는 batch를 $d = 0$인 부분과 무작위로 샘플링된 $d > 0$인 부분으로 나눈다. 따라서 다음과 같은 결합된 loss function을 얻을 수 있다.
\[\begin{equation} \mathcal{L}^S (\theta) = \mathbb{E}_{x_0 \sim \mathcal{N}, x_1 \sim \mathcal{D}, (t,d) \sim p(t,d)} \left[ \underbrace{\| s_\theta (x_t, t, 0) - (x_1 - x_0) \|^2}_{\textrm{Flow-Matching}} + \underbrace{\| s_\theta (x_t, t, 2d) - s_\textrm{target} \|^2}_{\textrm{Self-Consistency}} \right] \\ \textrm{where} \quad s_\textrm{target} = \frac{s(x_t, t, d) + s(x_{t+d}^\prime, t, d)}{2} \; \textrm{and} \; x_t + s_\theta (x_t, t, d) d \end{equation}\]직관적으로, 위의 loss는 모든 step 크기에 대해 noise에서 데이터로의 매핑을 일관되게 학습한다. Loss의 flow-matching 부분은 flow-matching model과 동일한 생성 능력을 개발한다. Self-consistency 부분에서 더 큰 step 크기에 대한 적절한 target은 두 개의 작은 shortcut 시퀀스를 연결하여 구성된다. 이를 통해 생성 능력이 여러 step에서 몇 step, 한 step으로 전파된다. 결합된 loss는 하나의 모델을 사용하고 한 번의 end-to-end 학습을 통해 공동으로 학습할 수 있다.

1. Training Details
Enforcing self-consistency
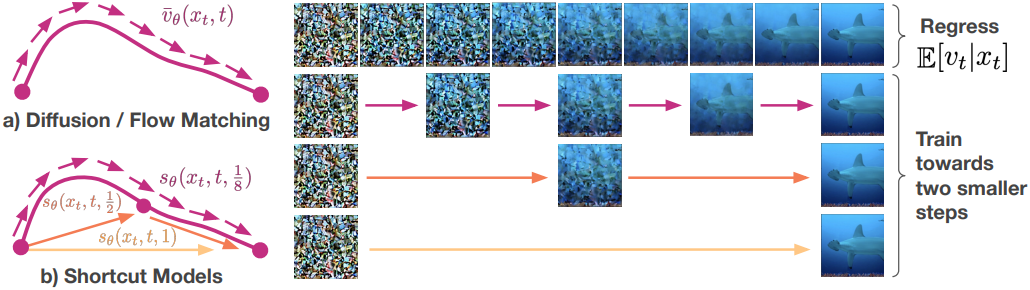
Shortcut model이 작은 step 크기에서 정확하다는 점을 감안할 때, shortcut model이 더 큰 step 크기에서도 이 동작을 유지하도록 하는 것이 중요하다. 이를 위해 자체 생성된 target에 의존한다. 근사 오차를 제한하기 위해 자체 생성할 target에 대한 경로의 길이를 제한하는 것이 바람직하다. 따라서 위 그림과 같이 저자들은 두 개의 shortcut을 사용하여 두 배 더 큰 shortcut을 구성하는 이진 재귀 방식을 선택하였다.
ODE를 근사하기 위한 가장 작은 시간 단위를 나타내는 step 수 $M$을 결정해야 한다. 저자들은 $M$으로 128을 사용하였으며, $d \in (1/128, 1/64, \ldots, 1/2, 1)$에 따라 총 8개의 shortcut 길이를 생성한다. 각 학습 step 동안 $x_t$, $t$, $d < 1$을 샘플링한 다음 shortcut model로 두 개의 연속적인 단계를 수행한다. 그런 다음 이 두 step의 연결을 target으로 사용하여 $2d$에 대해 모델을 학습시킨다.
두 번째 step은 학습 데이터에서 얻은 $x_t$가 아닌 denoising ODE에서 얻은 $x_{t+d}^\prime$를 사용한다. 즉, 데이터셋에서 $x_1$ 방향으로 보간하지 않고 예측된 첫 번째 shortcut을 $x_t$에 더해 구성한다. $d$가 가장 작은 값(1/128)일 때는 대신 $d = 0$에서 모델을 쿼리한다.
Joint optimization
Flow-matching loss와 self-consistency loss는 학습 중에 공동으로 최적화된다. Flow-matching 항은 랜덤 noise를 예측하기 때문에 분산이 훨씬 더 높은 반면, self-consistency loss는 deterministic한 target을 사용한다. 저자들은 self-consistency target보다 훨씬 더 많은 flow-matching target을 가진 batch를 구성하는 것이 도움이 된다는 것을 발견했다.
또한 self-consistency target은 두 번의 추가 forward pass가 필요하기 때문에 flow-matching target보다 생성하는 데 비용이 더 많이 든다. 따라서 flow-matching target과 self-consistency target을 3:1의 비율로 결합하여 학습 batch를 구성한다. 이런 식으로 동등한 diffusion model보다 약 16% 더 많은 컴퓨팅만 필요하도록 shortcut model의 학습 비용을 줄일 수 있다.
Guidance
Classifier-free guidance (CFG)는 diffusion model이 높은 생성 충실도를 위한 필수적인 도구임이 입증되었다. CFG는 class-conditional denoising ODE와 class-unconditional denoising ODE 사이의 상충 관계에 대한 선형 근사를 제공한다.
저자들은 CFG가 작은 step 크기에서는 도움이 되지만 선형 근사가 적절하지 않을 때 더 큰 step에서는 오차가 발생하기 쉽다는 것을 발견했다. 따라서 $d = 0$에서 shortcut model을 평가할 때는 CFG를 사용하지만 다른 곳에서는 사용하지 않는다.
Exponential moving average weights
최근의 많은 diffusion model은 가중치 파라미터에 대한 exponential moving average (EMA)를 사용하여 샘플 품질을 개선하였다. EMA는 생성에 평활화 효과를 유도하는데, 이는 loss에 내재적 분산이 있기 때문에 diffusion 모델링에서 특히 유용하다.
저자들은 shortcut model에서도 마찬가지로 $d = 0$에서의 loss의 분산이 $d = 1$에서 출력에 큰 진동을 일으킬 수 있음을 발견했다. Self-consistency target을 생성하기 위해 EMA 파라미터를 활용하면 이 문제가 완화된다.
Weight decay
저자들은 안정적인 학습에 weight decay가 매우 중요하다는 것을 발견했으며, 특히 학습 초기에 그렇다. 학습 초기에는 shortcut model 생성하는 self-consistency target은 대부분 noise이다. 모델은 이러한 target에 걸려 아티팩트와 나쁜 학습이 발생할 수 있다. 적절한 weight decay는 discretization schedule이나 신중한 warm-up 없이 이러한 문제를 사라지게 한다.
Discrete time sampling
실제로, 관련된 timestep에서만 학습시킴으로써 shortcut model의 부담을 줄일 수 있다. 학습하는 동안, 먼저 $d$를 샘플링한 다음, shortcut model이 쿼리될 지점에서만 $t$를 샘플링한다. 즉, 샘플링된 $t$는 $d$의 배수이다. 이러한 timestep $t$에서만 self-consistency loss를 학습시킨다.
Experiments
저자들은 추가로 Live Reflow라는 모델을 비교를 위해 추가하였다. Live Reflow는 flow-matching target으로 학습되는 모델과 self-consistency target으로 학습되는 모델을 각각 두고 동시에 학습시켜 one-step model을 얻는 방식이다.
1. Comparison
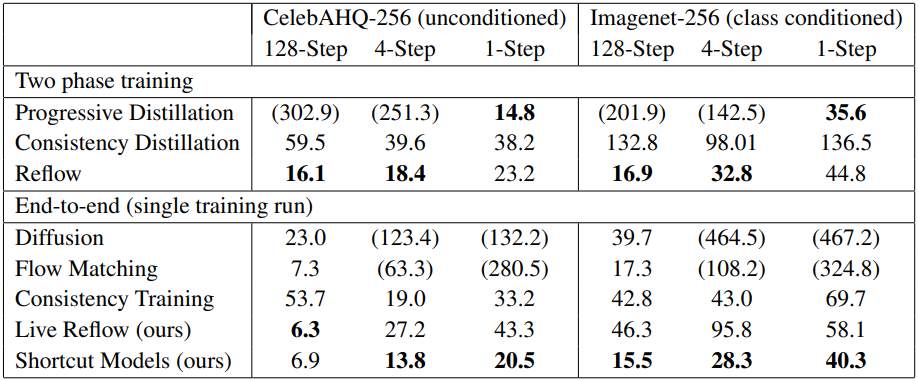
다음은 여러 생성 모델들의 이미지 생성 품질을 동일한 아키텍처 (DiT-B) 하에서 비교한 표이다.
2. Behavior of Shortcut Models
다음은 denoising step 수에 따른 shortcut model의 생성 품질을 flow-matching model과 비교한 결과이다.

3. Model Scale
다음은 모델 크기에 따른 one-step 생성 품질을 비교한 결과이다.

4. Latent Space Interpolation
저자들은 shortcut model의 latent space가 interpolation 가능한 지를 확인하고자 하였다. 초기 noise 샘플 쌍 ($x_0^0, x_0^1$)이 있을 때 다음 식과 같이 variance-preserving 방식으로 interpolation할 수 있다.
\[\begin{equation} x_0^n = n x_0^0 + \sqrt{1 - n^2} x_0^1 \end{equation}\]다음은 초기 noise 샘플 쌍을 interpolation한 결과이다.

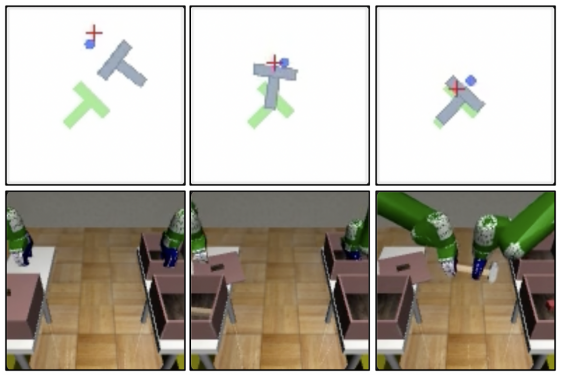
5. Nnon-image Domains
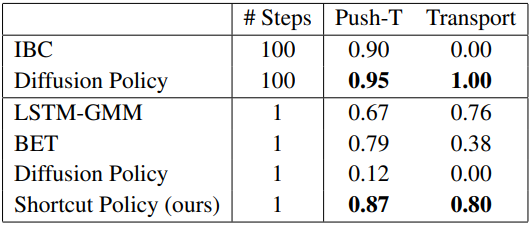
다음은 diffusion policy와 비슷한 방식으로 shortcut policy를 학습시킨 결과이다.
Limitations
- Noise와 데이터 간의 매핑이 데이터셋에 대한 기대값에 전적으로 의존한다.
- Multi-step 생성 품질과 one-step 생성 품질 간에 격차가 있다.