[논문리뷰] Unsupervised Discovery of Semantic Latent Directions in Diffusion Models
arXiv 2023. [Paper]
Yong-Hyun Park, Mingi Kwon, Junghyo Jo, Youngjung Uh
Department of Physics Education, Seoul National University | Department of Artificial Intelligence, Yonsei University
24 Feb 2023
Introduction
Diffusion model (DM)은 뛰어난 성능을 보여준 매우 강력한 생성 모델이다. 생성 프로세스를 제어하기 위해 기존 방법은 특히 text-to-image 합성 또는 다른 샘플링 프로세스의 latent 변수 $x_t$ 혼합을 위해 조건부 DM을 도입했다.
이러한 성공에도 불구하고 모델의 latent 변수 또는 중간 feature가 무엇인지 또는 결과 이미지에 어떻게 반영되는지에 대한 명확한 이해가 여전히 부족하다. Noisy한 이미지와 미묘한 noise의 시퀀스를 포함하는 DM의 특징적인 반복 프로세스 때문이라고 생각한다. 즉, 임베딩이 최종 이미지에 직접 연결되지 않는다. 반대로 GAN의 latent space에서 산술 연산을 수행하면 결과 이미지의 semantic이 변경된다. 이 속성은 실제 응용 프로그램을 위한 GAN 개발의 핵심 요소 중 하나였다. 저자들은 DM의 latent space에 대한 더 나은 이해가 유사한 개발을 촉진할 것이라고 가정하였다.
Diffusion models already have a semantic latent space 논문은 지정된 비대칭 샘플링 프로세스와 쌍을 이루는 semantic latent space $\mathcal{H}$로 diffusion kernel의 중간 feature space를 채택한다. DM의 잠재 공간에 대한 우리의 이해를 더하면서 $\mathcal{H}$의 로컬 선형성을 보였다. 그러나 latent 변수 $x_t$를 직접 처리하지 않고 proxy $h$에만 의존한다. 또한 편집 가능한 방향을 찾기 위해 CLIP과 같은 외부 supervision이 필요하다.
본 논문에서는 latent space $\mathcal{X}$에 대한 유용한 직관을 소개하여 사전 학습된 고정 diffusion model을 제어하는 방법에 대한 이해를 심화한다. 먼저, unsupervised 방식으로 리만 기하학을 사용하여 결과 이미지를 조작하는 $\mathcal{X}$의 semantic latent direction을 식별한다. 방향은 모델의 중간 feature space인 $\mathcal{X}$에서 $\mathcal{H}$로 매핑의 Jacobian의 특이값 분해에서 나온다. 아래 그림은 본 논문의 방법의 주요 개념을 보여준다.
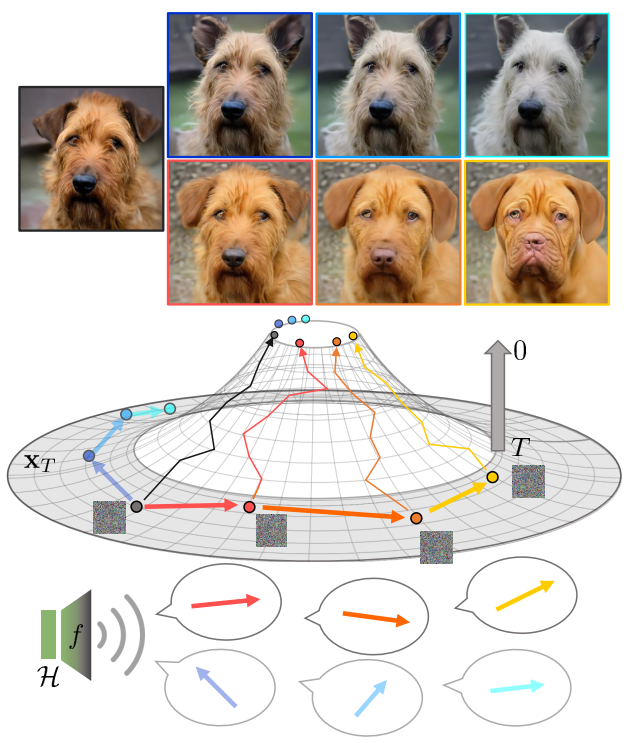
둘째, $\mathcal{H}$의 동질성을 이용하여 global semantic direction을 찾는다. 번거로운 샘플당 Jacobian 계산을 제거하고 일반적인 제어 가능성을 허용한다. GAN의 과정을 따르며, 샘플별 편집 방향을 글로벌한 편집 방향으로 확장한다.
마지막으로 diffusion model의 흥미로운 특성을 보여준다. $\mathcal{X}$에서 구형 선형 보간은 $\mathcal{H}$에서 거의 측지선(geodesic)이기 때문에 샘플 사이의 보간을 부드럽게 한다. 즉, $\mathcal{X}$는 뒤틀린 space이다. 초기 timestep은 저주파 성분을 생성하고 나중 timestep은 고주파 성분을 생성한다. 이를 power spectral density를 통해 명시적으로 보인다.
Editing with semantic latent directions
1. Pullback metric
Latent 변수 $x_t$가 존재하는 곡선 manifold $\mathcal{X}$를 생각하자. 미분 기하학은 각 점 $x$에서 정의된 vector space인 tangent space $\mathcal{T}_x$의 patch를 통해 $\mathcal{X}$를 나타낸다. 그런 다음 $\mathcal{X}$의 모든 기하학적 특성은 $\mathcal{T}_x$의 metric $| dx |^2 = \langle dx, dx \rangle _x$에서 얻을 수 있다. 그러나 $\langle dx, dx \rangle _x$에 대한 지식이 없다. 이는 분명히 Euclidean metric이 아니다. 또한 DM의 중간 timestep에서 $x_t$의 샘플에는 불가피한 noise가 포함되어 있어 semantic direction $\mathcal{T}_x$를 찾는 것을 막는다.
다행히 Diffusion models already have a semantic latent space 논문은 U-Net의 bottleneck layer에 의해 정의된 $\mathcal{H}$가 로컬 선형성을 나타내는 것을 관찰했다. 이를 통해 $\mathcal{H}$에 Euclidean metric을 사용할 수 있다. 미분 기하학에서 metric을 space에서 사용할 수 없으면 pullback metric이 사용된다. 원래 metric이 없는 space와 metric이 있는 space 사이에 부드러운 map이 존재하는 경우 매핑된 space의 pullback metric을 사용하여 원래 space의 거리를 측정한다. 본 논문의 아이디어는 $\mathcal{H}$에 pullback Euclidean metric을 사용하여 $\mathcal{X}$의 샘플 사이의 거리를 정의하는 것이다.
DM은 각 diffusion timestep에서 latent 변수 $x_t$에서 noise $t$를 추론하도록 학습된다. 각 $x_t$는 서로 다른 $t$에서 U-Net의 bottleneck 표현인 내부 표현 $h_t$를 갖는다. $\mathcal{X}$와 $\mathcal{H}$ 사이의 미분 가능한 map은 $f : \mathcal{X} \rightarrow \mathcal{H}$로 표시된다. 이하 간결하게 $x_t$를 $x$로 나타낸다. 본 논문의 방법은 denoising process의 모든 timestep에 적용될 수 있다.
그런 다음 미분 기하학은 $x$의 tangent space $\mathcal{T}_x$와 $h$의 $\mathcal{T}_h$ 사이의 linear map을 정의한다. Linear map은 벡터 \(v \in \mathcal{T}_x\)가 $u = J_x v$에 의해 벡터 $u \in \mathcal{T}_h$로 매핑되는 방식을 결정하는 Jacobian $J_x = \nabla_x h$로 설명할 수 있다. 실제로 Jacobian은 U-Net의 자동 미분을 통해 계산할 수 있다. 그러나 너무 많은 파라미터의 Jacobian은 다루기 어렵기 때문에 bottleneck 표현의 sum-pooling된 feature map을 $\mathcal{H}$로 사용한다.
$\mathcal{H}$의 로컬 선형성을 사용하여 metric $|dh|^2 = \langle dh, dh \rangle _h = dh^\top dh$를 Euclidean space에서 정의된 내적으로 가정한다. $\mathcal{X}$에 기하학적 구조를 할당하기 위해 대응되는 $\mathcal{H}$의 pullback metric을 사용한다. $v \in \mathcal{T}_x$의 pullback norm은 다음과 같이 정의된다.
\[\begin{equation} \| v \|_\textrm{pb}^2 \triangleq \langle dh, dh \rangle _h = v^\top J_x^\top J_x v \end{equation}\]2. Extracting the semantic directions and editing
Semantic latent directions
Pullback metric을 사용하여 \(v \in \mathcal{T}_x\)의 semantic direction을 추출할 수 있으며, 이는 대응되는 \(u \in \mathcal{T}_h\)의 큰 변동성을 보여준다. \(\| v \|_\textrm{pb}^2\)를 최대화하는 단위 벡터 $v_1$을 찾는다. 실제로 $v_1$은 $J_x = U \Lambda V^\top$의 특이값 분해의 첫 번째 right singular vector에 해당하며, 이는 $J_x^\top J_x = V \Lambda^2 V^\top$의 첫번째 eigenvector로 해석할 수 있다. $v_1$에 직교를 유지하면서 \(\|v\|_\textrm{pb}^2\)를 최대화하면 두 번째 단위 벡터 $v_2$를 얻을 수 있다. 이 process를 반복하면 $\mathcal{T}_x$의 $n$개의 semantic direction \(\{v_1, \cdots, v_n\}\)을 얻을 수 있다.
Jacobian $J_x$를 이용한 $\mathcal{T}_x$와 $\mathcal{T}_h$ 사이의 linear transformation을 사용하면 $\mathcal{T}_h$의 semantic direction도 얻을 수 있다.
\[\begin{equation} u_i = \frac{1}{\lambda_i} J_x v_i \end{equation}\]여기서 $u_i$를 $\Lambda$의 $i$번째 singular value $\lambda_i$로 나누어 정규화하였으며, 이를 통해 Euclidean norm $||u_i|| = 1$을 보존할 수 있다. 상위 $n$개의 큰 eigenvalue의 방향을 선택한 후 유한한 basis \(\{u_1, \cdots, u_n\}\)을 사용하여 $\mathcal{T}_h$의 모든 벡터를 근사할 수 있다. 앞으로 tangent space를 언급할 때 원래 tangent space의 $n$차원 low-rank approximation을 의미한다.
Iterative editing with geodesic shooting
이제 $x \rightarrow x’ = x + \gamma v_i$를 통해 $i$번째 semantic direction으로 샘플을 편집한다. 여기서 $\gamma$는 편집 크기를 제어하는 hyperparameter이다. 편집 강도를 높이려면 동일한 작업을 반복해야 한다. 그러나 이것은 $v_i$가 탄젠트 공간 \(\mathcal{T}_{x'}\)에서 벗어날 수 있기 때문에 작동하지 않는다. 따라서 추출된 방향을 새로운 tangent space로 재배치할 필요가 있다. 이를 위해 $v_i$를 새 tangent space \(\mathcal{T}_{x'}\)에 project하는 parallel transport을 사용한다. Parallel transport는 벡터가 manifold에 접하는 것을 유지하면서 가능한 한 방향을 바꾸지 않고 벡터를 이동한다. $\mathcal{X}$가 곡선 manifold이기 때문에 projection이 원래 벡터 $v_i$를 크게 수정한다는 점은 주목할 만하다. 그러나 $\mathcal{H}$는 비교적 평평하다. 따라서 $\mathcal{H}$에서 parallel transport를 적용하는 것이 유리하다.
$v_i$를 새로운 tangent space \(\mathcal{T}_{x'}\)에 project하기 위해 $\mathcal{H}$에서 parallel transport를 사용한다. 먼저 $\mathcal{T}_x$의 semantic direction $v_i$를 $\mathcal{T}_h$의 $u_i$로 변환한다. 둘째, parallel transport $u_i \in \mathcal{T}_h$를 \(u_i' \in \mathcal{T}_{h'}\)에 적용한다. 여기서 $h’ = f(x’)$이다.
Parallel transport에는 두 단계가 있다. 첫 번째 단계는 $u_i$를 새로운 tangent space에 project하는 것이다. 이 단계는 manifold에 접하는 벡터를 유지한다. 두 번째 단계는 project된 벡터의 길이를 정규화하는 것이다. 이 단계는 벡터의 크기를 유지한다. 셋째, $u_i’$ 를 $\mathcal{X}$로 변환하여 $v_i’$를 얻는다. $\mathcal{H}$를 통한 $v_i → v_i’$의 parallel transport를 사용하여
\[\begin{equation} x \rightarrow x' = x + \gamma v_i \rightarrow x'' = x' + \gamma v_i' \end{equation}\]의 다중 feature 편집을 실현할 수 있다. Jacobian의 정의에 따라 이 편집 프로세스는 $\mathcal{H}$에서 해당 방향으로 이동하는 것으로 볼 수 있다. 즉,
\[\begin{equation} h \rightarrow h' = h + \delta u_i \rightarrow h'' = h' + \delta u_i' \end{equation}\]이다. 이 반복 편집 절차는 자연스럽게 측지선(geodesic)을 형성하기 때문에 geodesic shooting이라고 한다. 아래 그림은 위의 절차를 요약한 것이다.
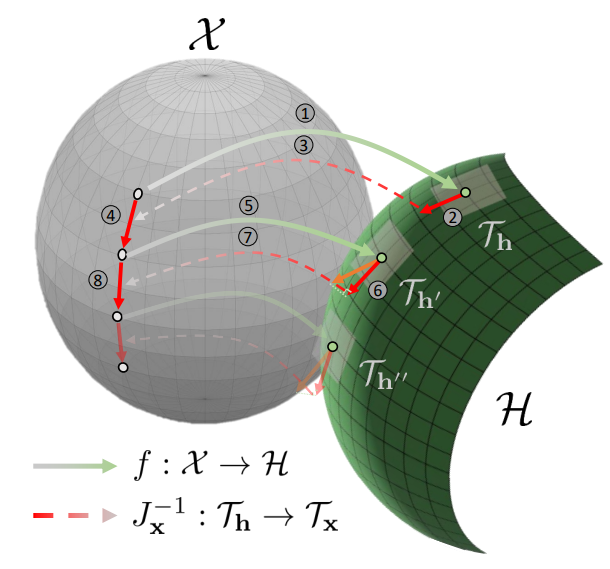
3. Global semantic directions
$x_t$ 편집을 위한 의미있는 방향을 추출했다. 그러나 semantic latent direction은 local이므로 $x_t$의 개별 샘플에만 적용할 수 있다. 따라서 모든 샘플에 대해 동일한 semantic 의미를 갖는 global semantic direction을 얻어야 한다. 저자들은 개별 샘플의 latent direction 사이에 큰 겹침을 관찰했다. 이 관찰은 $\mathcal{H}$가 global semantic direction을 갖는다는 가설을 세우도록 동기를 부여하였다.
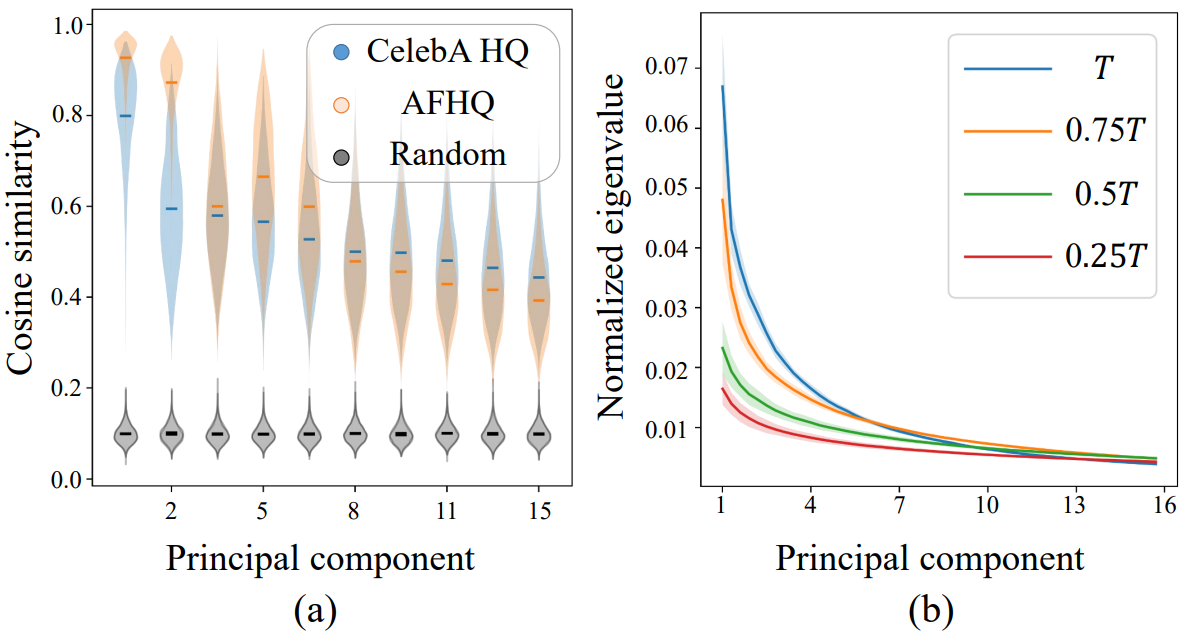
이 가설을 검증하기 위해 \(u_i^{(1)} \in \mathcal{T}_{h^{(1)}}\)에 대해 $u_i^{(1)}$와 크게 겹치는 \(u_j^{(2)} \in \mathcal{T}_{h^{(2)}}\)가 존재하는지 여부를 조사한다. 그런 다음 $x_t$의 많은 샘플 간에 $u_i^{(1)}$의 latent direction을 비교한다. $\lambda_i^{(1)}$과 $\lambda_j^{(2)}$의 큰 eigenvalue를 갖는 $u_i^{(1)}$과 $u_j^{(2)}$의 우세한 방향에 대해 항상 $t = T$일 때 두 단위 벡터가 상당히 겹치는 $(i, j)$를 항상 찾을 수 있다 (위 그림의 (a)). 따라서 $x_T$의 개별 샘플의 $\mathcal{H}$에서 가장 가까운 latent direction에 평균을 취하여 global semantic direction $\bar{u}_i$를 정의한다. Global direction은 샘플 $x$를 편집하는 데 사용할 수 있다. $\bar{u}_i$는 때때로 $\mathcal{T}_h$의 local tangent space에서 벗어날 수 있다. 이 탈출을 완화하기 위해 $\bar{u}_i$를 $\mathcal{T}_h$에 project한다. 본 논문의 방법은 $\mathcal{X}$에서 샘플을 편집하기 때문에 Jacobian을 통해 $\bar{u}_i$를 $\mathcal{T}_x$의 해당 방향 $\bar{v}_i$로 변환한다.
그러나 작은 $t$의 $x_t$에 대해서 본 논문의 가설을 적용하는 것은 신중해야 한다. 저자들은 서로 다른 $t$ 사이의 eigenvalue 스펙트럼을 비교하고 $t$가 0에 가까울수록 더 평평해지는 것을 관찰했다 (위 그림의 (b)). 이것은 $x_T$에 대해서는 몇 가지 지배적인 feature direction이 존재하는 반면 작은 $t$를 가진 $x_t$에 대해서는 다양한 feature direction이 존재함을 보여준다. 그러면 local feature direction의 동질성을 기반으로 global direction을 정의하기 어렵다.
4. Normalizing distortion due to editing
DM은 $x_T \rightarrow x_{T-1} \rightarrow \cdots \rightarrow x_0$으로 반복적으로 denoising하여 이미지를 생성한다. $x_t \rightarrow x_t + \gamma v_i$로 $x_t$의 이미지를 편집한다고 가정하자. $v_i$의 편집 신호는 denoising process 전반에 걸쳐 전파되고 증폭된다. 증폭으로 인해 $x_0$ 생성 시 예기치 않은 아티팩트가 발생할 수 있다. 이 문제를 방지하려면 편집 후 $x_t$의 일부 정규화가 필요하다. 그러나 white noise가 섞인 $x_t$ 내부 신호만 정규화하기는 어렵다. 여기서 저자들은 개선된 편집 방법을 제안한다.
DDIM은 예측된 noise $\epsilon_t^\theta (x_t)$로 $x_t$에서 $x_0$를 계산한다.
\[\begin{equation} x_0 = \frac{x_t - \sqrt{1 - \alpha_t} \epsilon_t^\theta (x_t)}{\sqrt{\alpha_t}} \end{equation}\]$x_0 (x_t)$를 $x_t$의 함수로 둔다. 이상적인 시나리오에서 $x_0 (x_t)$는 정규화 프로세스를 단순화하는 $x_t$의 신호만 포함한다고 가정할 수 있다. 개선된 편집 방법은 세 단계로 구성된다.
- 원본 이미지를 $x_t \rightarrow x_t + \gamma v_i$로 편집한다.
- 편집 후 신호를 보존하기 위해 $x_0 (x_t + \gamma v_i)$를 정규화한다. 정규화는 $x_0 (x_t + \gamma v_i)$의 픽셀 간 표준 편차를 정규화하고 평균 픽셀 값을 고정하여 구현된다. 정규화된 $x_0 (x_t + \gamma v_i)$를 $x_0’$으로 나타낸다.
- $x_t’$에 대한 DDIM 방정식
$\quad$ 을 풀어 $x_t + \gamma v_i$에서 파생될 수 있는 해당 편집 샘플을 얻는다. 1차 Taylor expansion
\[\begin{equation} \epsilon_t^\theta (x_t') \approx \epsilon_t^\theta (x_t) + \nabla_{x_t} \epsilon_t^\theta (x_t) \cdot (x_t' − x_t) \end{equation}\]$\quad$ 를 사용하여 업데이트된 방정식을 얻는다.
\[\begin{equation} x_t' = x_t + \frac{\sqrt{\alpha_t}}{1 - \kappa \sqrt{1 - \alpha_t}} (x_0' - x_0 (x_t)) \end{equation}\]여기서 $\kappa = 0.99$를 사용한다.
Experiment
- 데이터셋: CelebA-HQ (DDPM++), AFHQ-dog (iDDPM)
- 해상도: $256^2$
1. Image manipulation
Semantic latent directions
다음은 CLIP이나 다른 classifier와 같은 supervision 없이 본 논문의 방법으로 찾은 direction으로 편집한 결과의 예시이다.

Direction에는 성별, 연령, 민족, 표정, 품종, 질감과 같은 semantic이 명확하게 포함되어 있다. 흥미롭게도 timestep $T$에서의 편집은 머리 색깔, 머리 길이, 먼 품종과 같은 대략적인 변화로 이어진다. 반면 timestep $0.5T$에서의 편집은 메이크업, 머리결, 주름, 표정 등 디테일한 변화로 이어진다.
Editing timing
다음은 다양한 timestep에 대한 direction을 비교한 것이다.
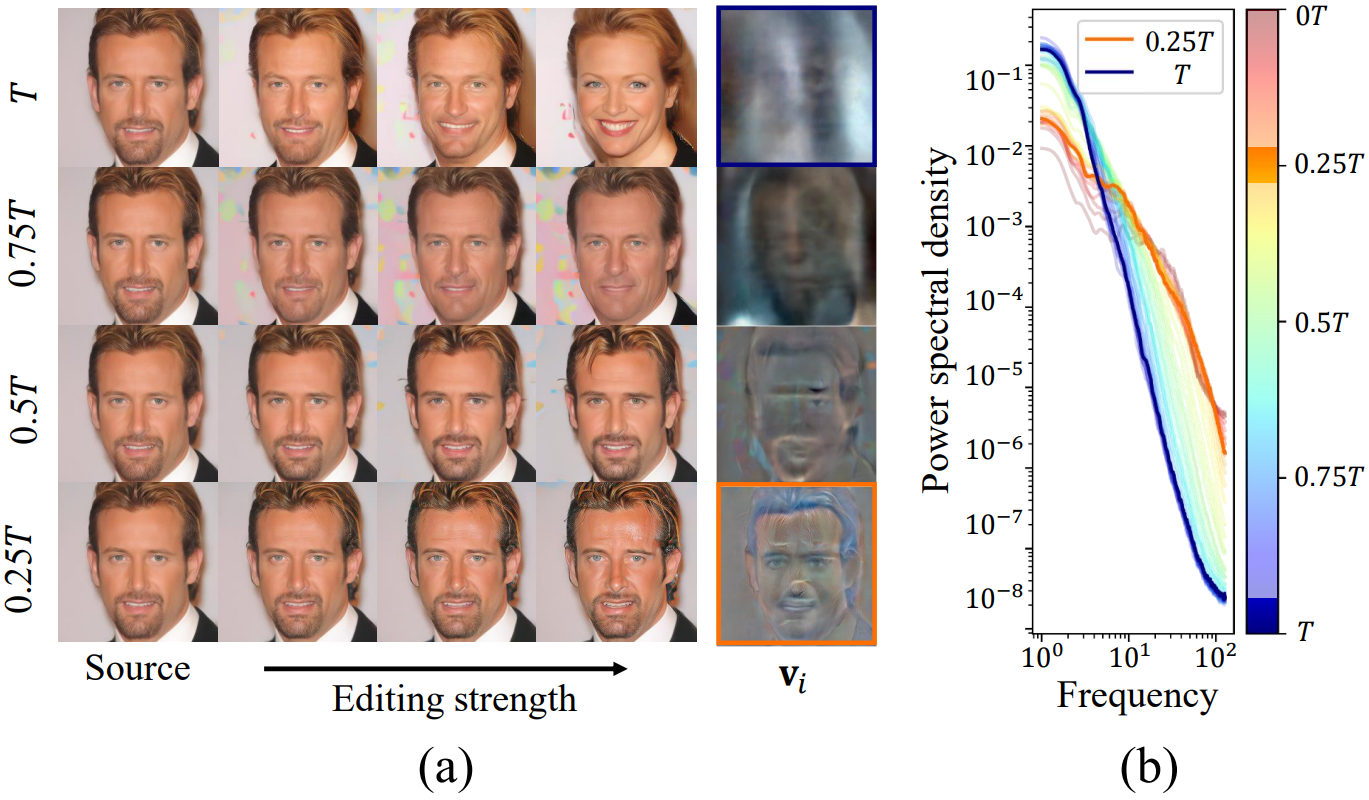
(a)는 여러 timestep에 대한 $v_i$의 예시를 보여준다. $T$에서 $v_i$는 $x_T$의 흐릿한 변화에 의해 $x_0$의 대략적인 속성 변화로 이어진다. $0.25T$에서 $v_i$는 $x_0$ 와 $x_t$ 모두에서 고주파 디테일을 편집한다. (b)는 $v_i$의 power spectral density (PSD)를 보여준다. 초기 timestep은 나중 timestep보다 저주파의 더 많은 부분을 포함하고 나중 timestep은 고주파의 더 많은 부분을 포함한다. 이러한 현상은 편집된 이미지의 경향과 일치한다. 이 결과는 timestep에 대한 일반적인 이해를 강화한다.
Global semantic directions
다음은 global semantic direction으로 편집한 예시 이미지들이다.

$x_t$의 global direction은 같은 semantic 변경을 이끈다. 이는 $\mathcal{X}$가 metric이 없는 space지만 pullback metric을 통해 $\mathcal{X}$가 $\mathcal{H}$의 동질성을 상속함을 확인한다.
2. Curved manifold of DMs
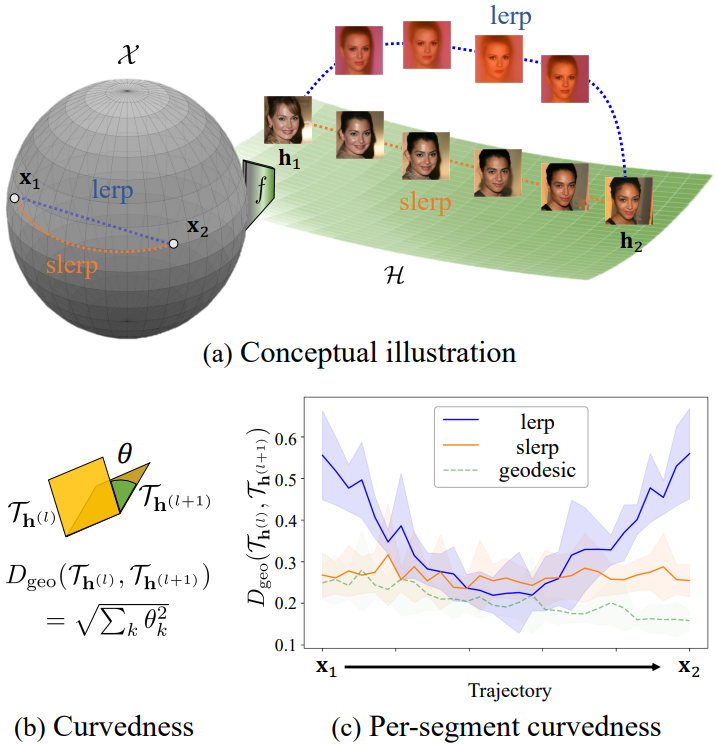
저자들은 $\mathcal{X}$가 곡선 manifold라는 가정의 경험적 기반을 제공하였다. Manifold 위의 두 점 사이의 semantic path 길이는 manifold를 따라 두 지점을 연결하는 선분의 로컬한 뒤틀림의 합으로 정의된다. 선분 \(\{x^{(1)}, x^{(2)}\}\)의 curvedness를 \(\{h^{(1)}, h^{(2)}\}\)에 중심을 둔 두 tangent space의 각도로 정의하기 위해 geodesic metric을 사용한다.
여기서 $\theta_k = \cos^{-1} (\sigma_k)$는 \(\mathcal{T}_{h^{(1)}}\)와 \(\mathcal{T}_{h^{(ㅈ)}}\)의 $k$번째 principle angle 사이의 각도이다. 이 각도는 위 그림의 (b)에 시각화되어 있다.
그러면 semantic path 길이는
\[\begin{equation} \sum_l D_\textrm{geo} (\mathcal{T}_{h^{(l)}}, \mathcal{T}_{h^{(l+1)}}) \end{equation}\]이 되며, $l$은 경로의 segment index이고 30으로 설정된다. 경로가 manifold에서 멀어질수록 semantic path 길이가 증가한다.
가정을 검증하기 위해 서로 다른 경로(linear path, spherical path, geodesic shooting path)의 semantic path 길이를 비교한다. 위 그림의 (a)는 manifold, linear path (lerp), spherical path (slerp)와 함수 $f$에 의해 매핑된 $\mathcal{H}$의 해당 경로를 시각화한 것이다. 저자들은 랜덤하게 선택된 50개의 이미지 쌍에 대한 semantic path 길이를 계산했다. 위 그림의 (c)는 경로를 따라 segment 길이의 분포를 보여준다. 흥미롭게도 lerp의 길이는 끝 부분이 높고 중앙 근처에서 geodesic의 길이로 줄어든다. 저자들은 lerp 경로가 원래 manifold에서 멀어지고 다른 manifold를 따라 이동한다고 가정한다.

위 표는 slerp의 semantic path 길이가 lerp보다 작다는 것을 보여주며, 이는 slerp 경로가 lerp보다 manifold에 더 가깝다는 것을 나타낸다. 즉, manifold가 곡선이다.
Semantic path 길이는 interpolation path를 따른 합산에 관한 perceptual path length(PPL)와 유사하다. PPL은 경로를 따라 결과 이미지 사이의 LPIPS 거리를 측정한다. 두 개의 latent 변수 사이의 PPL이 높을수록 아티팩트를 수반하는 이미지의 interpolation이 더 뾰족해짐을 나타낸다. 반면에 semantic path 길이는 인접한 tangent space 사이에서 기하학적 구조가 얼마나 급격하게 변하는지를 측정한다.
3. Stable Diffusion
다음은 Stable Diffusion으로 일반화한 예시를 보여준다.

4. Ablation study
아래 그림 semantic direction의 중요성을 보여준다.

랜덤한 direction이 이미지를 심각하게 손상시킴을 보여준다.
아래 그림은 정규화의 필요성을 보여준다.

본 논문의 방법은 극단적인 변화에도 그럴듯한 편집 이미지를 생성하지만 정규화를 제거하면 과도한 채도가 발생한다.
5. Comparison to other editing methods
GAN에서 $\mathcal{Z}$에서 $\mathcal{W}$로 매핑하는 대신 $\mathcal{X}$에서 $\mathcal{H}$로 매핑하는 것을 고려하여 GANSpace와 본 논문의 방법을 비교한다. 따라서 PCA를 사용하여 $\mathcal{H}$에서 direction을 찾는다.

위 그림은 그 효과를 보여준다. 속성을 다소 변경하지만 심각한 왜곡이나 얽힘을 수반한다. 반대로 본 논문의 방법은 이전 결과에서 볼 수 있듯이 적절한 조작으로 이어지는 기하학적 구조를 고려하여 $\mathcal{H}$의 변화가 가장 큰 방향을 찾는다.
Limitations
Semantic latent direction이 일반적으로 disentanglement를 강제하기 위해 속성 주석을 사용하지 않더라도 disentangle한 속성을 전달한다는 것은 흥미롭다. 저자들은 U-Net에서 인코더의 Jacobian을 분해하면 자연스럽게 어느 정도 disentanglement가 발생한다고 가정하였다. U-Net에서 중간 feature space $\mathcal{H}$의 선형성을 기반으로 한다. 그러나 완벽한 disentanglement를 보장하는 것은 아니며 일부 direction이 얽혀 있다.

예를 들어, 긴 머리의 direction은 위 그림의 (a)와 같이 남성 피사체를 여성으로 변환한다. 이러한 종류의 얽힘은 이전 데이터셋으로 인해 다른 편집 방법에서 종종 발생한다 (긴 머리를 가진 남성 얼굴이 거의 없다).
본 논문의 방법이 Stable Diffusion에도 유효하다는 것을 보여 주었지만 여전히 더 많은 관찰이 필요하다. 위 그림의 (b)와 같이 Stable Diffusion에서 편집 절차 중에 semantic latent direction의 수가 적고 가끔 급격한 변화를 전달하는 direction이 거의 없음을 발견할 수 있다. 저자들은 학습된 latent space가 이미지 space보다 더 복잡한 manifold를 가질 수 있다고 가정하였다. 또는 classifier-free guidance 또는 cross-attention mechanism이 있는 조건부 DM은 manifold에 복잡성을 추가할 수 있다.