[논문리뷰] Semantic Image Synthesis via Diffusion Models
arXiv 2022. [Paper]
Weilun Wang, Jianmin Bao, Wengang Zhou, Dongdong Chen, Dong Chen, Lu Yuan, Houqiang Li
University of Science and Technology of China (USTC) | Microsoft Research Asia | Microsoft Cloud+AI
30 Jun 2022

Introduction
Semantic image synthesis는 semantic layout을 기반으로 실사 이미지를 생성하는 것을 목표로 하며, semantic segmentation의 반대 문제이다. 최근 연구는 주로 네트워크가 reconstruction loss와 함께 adversarial loss로 학습되는 적대적 학습 패러다임을 따른다. 모델 아키텍처를 탐색함으로써 벤치마크 데이터셋에서 성능을 점진적으로 향상시킨다. 그러나 기존의 GAN 기반 접근 방식은 일부 복잡한 장면에서 높은 fidelity와 다양한 결과를 생성하는 데 한계가 있다.
DDPM(Denoising Diffusion Probabilistic Model)은 최대 likelihood 학습을 기반으로 하는 새로운 종류의 생성 모델이다. DDPM은 반복적인 denoising process를 통해 표준 가우시안 분포에서 경험적 분포로 샘플을 생성한다. 생성된 결과의 점진적 개선을 통해 여러 이미지 생성 벤치마크에서 state-of-the-art 샘플 품질을 달성하였다.
본 논문에서는 semantic image synthesis 문제에 대한 diffusion model 탐색의 첫 번째 시도를 제시하고 Semantic Diffusion Model (SDM)이라는 새로운 프레임워크를 디자인한다. 프레임워크는 denoising diffusion 패러다임을 따르며 반복적인 denoising process를 통해 샘플링된 Gaussian noise를 사실적인 이미지로 변환한다. 생성 프로세스는 parameterize된 Markov chain이다. 각 step에서 semantic label map에 따라 조정된 denoising network에 의해 입력된 noisey한 이미지에서 noise가 추정된다. 추정된 noise에 따라 사후 확률 공식을 통해 noise가 적은 이미지가 생성된다. 반복을 통해 denoising network는 semantic 관련 콘텐츠를 점진적으로 생성하고 이를 denoising stream에 주입하여 사실적인 이미지를 생성한다.
Denoising network의 입력으로 조건 정보를 noisy한 이미지와 직접 연결하는 이전의 조건부 DDPM을 다시 살펴본다. 이 접근 방식은 입력 semantic mask의 정보를 완전히 활용하지 못하므로 이전 연구에서처럼 생성된 이미지의 품질과 의미론적 상관관계가 낮다. 이에 동기를 부여받아 semantic layout과 noisy한 이미지를 독립적으로 처리하는 조건부 denoising network를 설계한다. Semantic layout이 multi-layer spatially-adaptive normalization (SPADE) 연산자에 의해 denoising network의 디코더에 임베딩되는 동안 noisy한 이미지는 denoising network의 인코더에 공급된다. 이것은 생성된 이미지의 품질과 의미론적 상관관계를 크게 향상시킨다.
또한 diffusion model은 본질적으로 다양한 결과를 생성할 수 있다. 샘플링 전략은 생성된 결과의 품질과 다양성의 균형을 맞추는 데 중요한 역할을 한다. Naive한 샘플링 절차는 높은 다양성을 보여주지만 semantic label map과의 사실감 및 강력한 대응이 부족한 이미지를 생성할 수 있다. Classifier-free guidance 전략을 채택하여 이미지 fidelity와 의미론적 대응을 향상한다. 특히 semantic mask 입력을 랜덤하게 제거하여 사전 학습된 diffusion model을 finetuning한다. 그런 다음 semantic mask가 있거나 없는 diffusion mask의 예측을 기반으로 샘플링 전략이 처리된다. 이 두 상황의 score를 보간함으로써 샘플링 결과는 semantic mask 입력과 더 높은 fidelity 및 더 강한 상관관계를 달성한다.
Methodology
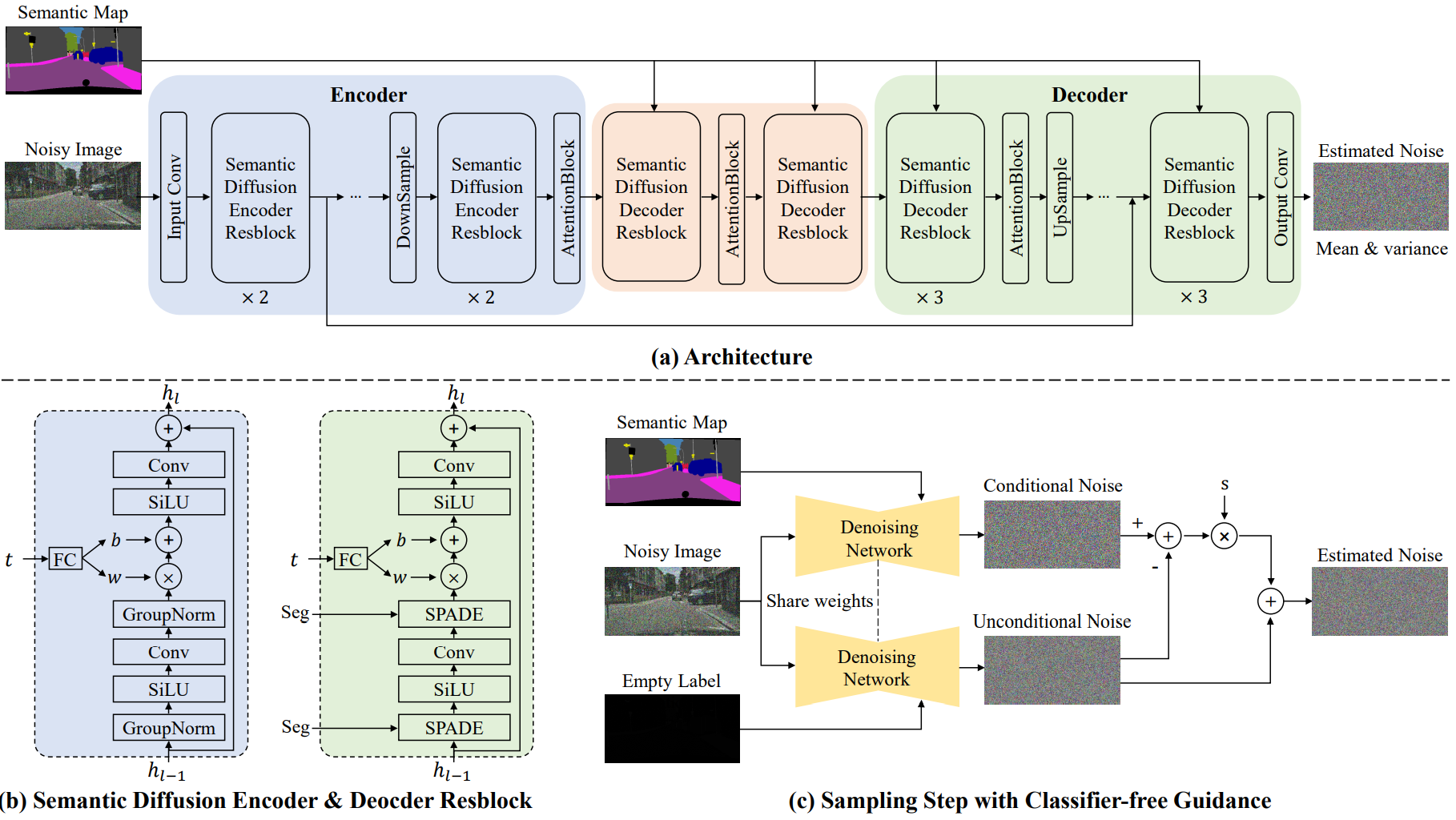
1. Semantic Diffusion Model
위 그림의 (a)는 SDM의 조건부 denoising network의 개요이다. 기존의 조건부 diffusion model과 다르게 denoising network는 semantic label map과 noisy한 이미지를 독립적으로 처리한다. Noisy한 이미지는 인코더 부분에 들어가고 semantic label map은 multi-layer SPADE 연산으로 디코더에 주입된다.
Encoder
Noisy한 이미지의 feature는 semantic diffusion encoder resblock (SDEResblock)과 attention block으로 인코딩된다. 위 그림의 (b)는 SDEResblock의 디테일한 구조를 보여주며, convolution, SiLU, group normalization으로 구성된다. SiLU는 깊은 모델에서 ReLU보다 더 좋은 결과를 내는 경향이 있는 활성화 함수이며, $f(x) = x \cdot \textrm{sigmoid}(x)$이다. 여러 timestep $t$에서 network가 noise를 추정하도록 하기 위해 SDEResblock은 중간 activation을 학습 가능한 가중치 $w(t) \in \mathbb{R}^{1 \times 1 \times C}$와 bias $b(t) \in \mathbb{R}^{1 \times 1 \times C}$로 scaling되고 shifting된다.
\[\begin{equation} f^{i+1} = w(t) \cdot f^i + b(t) \end{equation}\]$f^i, f^{i+1} \in \mathbb{R}^{H \times W \times C}$은 각각 입력과 출력 feature이다. Attention block은 skip-connection을 가진 self-attention block이다.
\[\begin{equation} f(x) = W_f x, \quad g(x) = W_g x, \quad h(x) = W_h x \\ \mathcal{M} (u, v) = \frac{f(x_u)^\top g(x_v)}{\|f(x_u)\| \|g(x_v)\|} \\ y_u = x_u + W_v \sum_v \textrm{softmax}_v (\alpha \mathcal{M}(u,v)) \cdot h (x_v) \end{equation}\]$x$와 $y$는 attention block의 입력과 출력이고 $W_f, W_g, W_h, W_v \in \mathbb{R}^{C \times C}$는 1$\times$1 convolution block이다. $u$와 $v$는 공간 차원의 인덱스로 범위는 1부터 $H \times W$까지이다. Attention block은 특정 해상도에서만 적용된다. (32$\times$32, 16$\times$16, 8$\times$8)
Decoder
Denoising network의 디코더에 semantic label map을 주입하여 denoising 과정을 guide한다. 기존 조건부 diffusion model에서는 조건 정보와 noisy한 입력을 직접 concat하여 입력으로 사용한다. 저자들은 이 접근 방식이 semantic 정보를 충분히 활용하지 못한다는 것을 발견했다. 이 문제를 해결하기 위하여 semantic diffusion decoder resblock (SDDResblock)을 디자인하여 semantic level map을 multi-layer spatially-adaptive 방법으로 디코더에 임베딩한다. SDEResblock과는 다르게 group normalization 대신 spatially-adaptive normalization (SPADE)를 사용한다. SPADE는 denoising stream에 semantic level map을 주입한다.
\[\begin{equation} f^{i+1} = \gamma^i (x) \cdot \textrm{Norm} (f^i) + \beta^i (x) \end{equation}\]$\textrm{Norm}$은 parameter가 없는 group normalization이다. $\gamma^i (x)$와 $\beta^i (x)$는 spatially-adaptive weight과 bias이다. SDM은 attention block, skip-connection, timestep embedding module을 포함하는 diffusion process를 위하여 디자인되었으므로 SPADE와 다르다.
3. Loss functions
SDM은 두가지 목적 함수로 학습된다. 첫번째 목적 함수는 simple diffusion loss이다. 레퍼런스 출력 이미지 $y$와 랜덤 timestep \(t \in \{0, 1, \cdots, T\}\)가 주어지면 $y$의 noisy한 버전 $\tilde{y}$는 다음과 같이 생성된다.
\[\begin{equation} \tilde{y} = \sqrt{\vphantom{1} \bar{\alpha}_t} y + \sqrt{1 - \bar{\alpha}_t} \epsilon, \quad \epsilon \sim \mathcal{N}(0,I) \end{equation}\]$\alpha_t$는 $t$에서의 noise schedule이다. SDM애서 $T = 1000$으로 둔다. 조건부 diffusion model은 semantic layout $x$의 guidance 하에서 noise $\epsilon$을 예측하여 $y$를 재구성하도록 학습된다.
\[\begin{equation} \mathcal{L}_\textrm{simple} = \mathbb{E}_{t, y, \epsilon} = [\| \epsilon - \epsilon_\theta(\sqrt{\vphantom{1} \bar{\alpha}_t} y + \sqrt{1 - \bar{\alpha}_t} \epsilon, x, t) \|_2] \end{equation}\]Improved DDPM을 따라 network는 추가로 분산 $\Sigma_\theta (\tilde{y}, x, t)$을 예측하도록 학습되어 생성된 이미지의 log-likelihood를 개선한다. 조건부 diffusion model은 추가로 보간 계수 $v$를 출력하며, 분산은 다음과 같다.
\[\begin{equation} \Sigma_\theta (\tilde{y}, x, t) = \exp (v \log \beta_t + (1-v) \log \tilde{\beta}_t) \end{equation}\]두번째 목적 함수는 추정된 분포 $p_\theta (y_{t-1} \vert y_t, x)$와 diffusion process의 사후 확률 $q(y_{t-1} \vert y_t, v_0)$ 사이의 KL divergence를 직접 최적화한다.
\[\begin{equation} \mathcal{L}_\textrm{vlb} = \textrm{KL} (p_\theta (y_{t-1} \vert y_t, x) \| q (y_{t-1} \vert y_t, y_0)) \end{equation}\]전체 loss는 두 목적 함수의 가중합이다.
\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{simple} + \lambda \mathcal{L}_\textrm{vlb} \end{equation}\]$\lambda$는 loss function의 균형을 맞추기 위한 trade-off paramter이다.
4. Classifier-free guidance.
DDPM의 일반적이 샘플링 과정을 따르면 이미지가 다양하게 생성되지만 현실적이지 않으며 semantic label map과 강하게 연관되지 않는다. 저자들은 조건부 diffusion model이 조건부 입력을 샘플링 프로세스 중에 잘 다루지 못한다고 가정하였다. 이전 연구들은 조건부 diffusion model의 샘플을 로그 확률의 기울기
\[\begin{equation} \nabla_{y_t} \log p(x \vert y_t) \end{equation}\]로 개선시켰다. 추정된 평균이 $\mu_\theta (y_t \vert x)$고 추정된 분산이 $\Sigma_\theta (y_t \vert x)$라고 하면 다음과 같이 평균을 교란하여 결과를 개선시킬 수 있다.
\[\begin{equation} \hat{\mu}_\theta (y_t \vert x) = \mu_\theta (y_t \vert x) + s \cdot \Sigma_\theta (y_t \vert x) \cdot \nabla_{y_t} \log p(x \vert y_t) \end{equation}\]$s$는 guidance scale이라는 hyperparamter이며, 샘플 품질과 다양성을 절충한다.
이전 연구에서는 추가로 학습된 classifier $p(x \vert y_t)$를 적용하여 샘플링 프로세스 중에 기울기를 제공한다. Classifier-free diffusion guidance 논문에서 영감을 받아, 학습에 추가 비용이 필요한 classifier model 대신 생성 모델 자체로 guidance를 얻는다. 주요 아이디어는 semantic label map $x$를 null label $\emptyset$로 교체하여 $\epsilon_\theta (y_t \vert \emptyset)$에서 $\epsilon_\theta (y_t \vert x)$의 guidance에 따라 추정된 noise를 분리한다. 분리된 요소는 로그 확률의 기울기를 암시적으로 추론한다.
\[\begin{aligned} \epsilon_\theta (y_t \vert x) - \epsilon_\theta (y_t \vert \emptyset) & \propto \nabla_{y_t} \log p (y_t \vert x) - \nabla_{y_t} \log p (y_t) \\ & \propto \nabla {y_t} \log p (x \vert y_t) \end{aligned}\]샘플링 과정 중에 조건부 diffusion model의 샘플을 개선하기 위해 이 분리된 요소가 증가한다.
\[\begin{equation} \tilde{\epsilon}_\theta (y_t \vert x) + s \cdot (\epsilon_\theta (y_t \vert x) - \epsilon_\theta (y_t \vert \emptyset)) \end{equation}\]본 논문에서 $\emptyset$은 영벡터로 정의된다.
Experiments
- 데이터셋: Cityscapes (256$\times$512) / ADE20K, CelebAMask-HQ, COCO-Stuff (256$\times$256)
- Evaluation
- 시각적 품질: FID (Frechet Inception Distance)
- 다양성: LPIPS
- correspondence: 상용 네트워크로 semantic interpretability을 평가
- Cityscapes는 DRN-D-105, ADE20K는 UperNet101, CelebAMask-HQ는 Unet, COCO-Stuff는 DeepLabV2를 사용
- 생성된 이미지와 semantic layout으로 mIoU (mean IoU)를 계산
- mIoU가 상용 네트워크의 능력에 의존
1. Comparison with previous methods
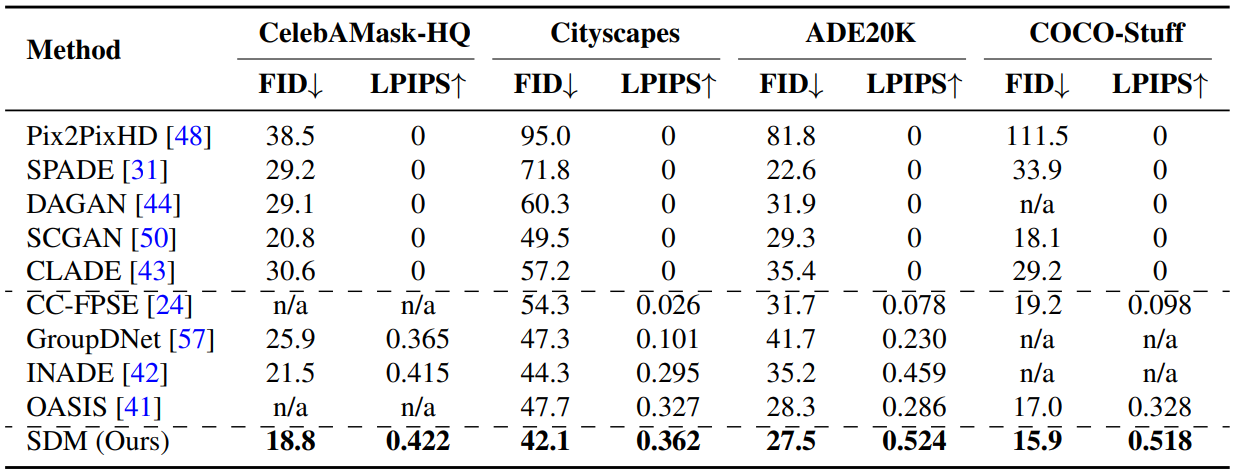
다음은 semantic image synthesis에 대한 기존 방법들과의 정량적 평가 표이다.
다음은 CelebAMask-HQ, ADE20K, Cityscapes. COCO-Stuff에서의 샘플들을 비교한 것이다.




다음은 4개의 데이터셋에 대하여 본 논문의 결과를 다양한 다른 방법들의 결과보다 선호하는 비율을 나타낸 user study이다.

다음은 본 논문의 모델로 생성한 multimodal 생성 결과이다. 고품질의 다양한 결과를 생성하는 것을 볼 수 있다.

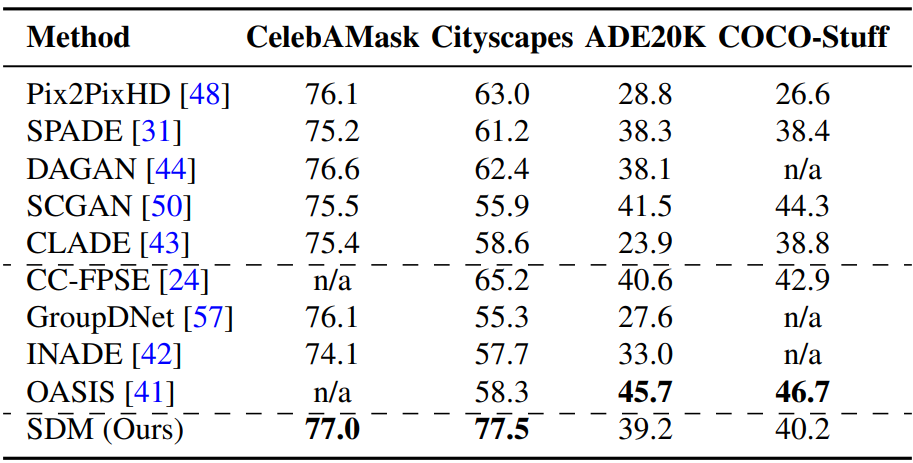
다음은 4개의 데이터셋에 대하여 mIoU를 측정한 표이다.
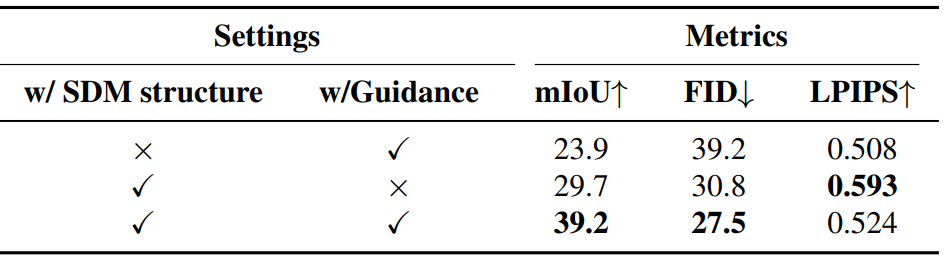
2. Ablation Studies
다음은 조건 정보의 임베딩과 classifier-free guidance 전략에 대한 ablation study 결과이다.
다음은 ablation 실험의 정성적 결과를 비교한 것이다.

3. Controlled Generation
다음은 SDM의 semantic image editing의 예시이다. 녹색 부분이 지워진 부분이며, 모델은 편집된 semantic map을 기반으로 inpainting을 한다.
