[논문리뷰] Self-Calibrating Gaussian Splatting for Large Field-of-View Reconstruction

ICCV 2025 (Highlight). [Paper] [Page] [Github]
Youming Deng, Wenqi Xian, Guandao Yang, Leonidas Guibas, Gordon Wetzstein, Steve Marschner, Paul Debevec
Cornell University | Netflix Eyeline Studio | Stanford University
13 Feb 2025

Introduction

본 논문에서는 렌즈 왜곡, 카메라 intrinsic, 카메라 포즈, 장면 표현을 3D Gaussian을 이용하여 동시에 최적화하는 미분 가능한 rasterization 파이프라인인 Self-Calibrating Gaussian Splatting을 소개한다. 본 접근 방식은 리샘플링, 사전 calibration, 다항식 distortion 모델 없이도 넓은 FOV의 이미지에서 고품질 재구성을 달성하였다.

렌즈 모델링을 개선하기 위해, 신경망을 사용하는 기존의 distortion 모델을 표현력과 계산 효율성의 균형을 맞춘 새로운 하이브리드 신경망 모델로 대체했다. 본 논문의 방법은 invertible ResNet을 사용하여 정규화된 sparse 그리드에서 변위를 예측한 후, bilinear interpolation을 통해 연속적인 distortion field를 생성한다.

단일 평면 시점으로 리샘플링할 때 발생하는 늘어짐을 완화하기 위해 cubemap 샘플링을 사용한다. 이는 늘어짐을 크게 줄이고 주변 영역에서도 픽셀 밀도를 더욱 균일하게 만든다. Gaussian들은 cubemap의 각 90° FOV 면에 projection된다.

마지막으로, 본 논문에서 제시하는 방법은 렌즈 calibration, bundle adjustment, 장면 재구성을 통합된 end-to-end 프로세스로 결합하여 모든 미지수에 대한 렌더링 loss를 최소화함으로써 사전 calibration에 비해 재구성 오차를 줄인다.

Method

1. Lens Distortion Modeling

본 논문에서는 렌즈 왜곡 모델링을 통해 fisheye 렌즈 및 광각 카메라를 포함한 더 넓은 FOV의 카메라 렌즈에 적용할 수 있도록 Gaussian Splatting 기법을 확장하였다. 렌즈 왜곡은 일반적으로 카메라 좌표계에서 정의된 distortion function \(\mathcal{D}_\theta : \mathbb{R}^2 \rightarrow \mathbb{R}^2\)으로 표현되며, 보정된 이미지의 픽셀 위치를 왜곡된 이미지의 위치로 매핑한다. 이상적으로, \(\mathcal{D}_\theta\)는 다음과 같은 요구 사항을 만족해야 한다.

1. 다양한 렌즈 왜곡을 모델링할 수 있을 만큼 충분히 표현력이 풍부해야 한다.
2. 3D 장면과 함께 최적화될 수 있도록 정규화가 잘 되어 있어야 한다.
3. 계산 오버헤드를 크게 증가시키지 않을 만큼 효율적이어야 한다.

기존 접근 방식 중 어느 것도 세 가지 기준을 모두 완벽하게 만족시키지는 못했다.

Grid-based method

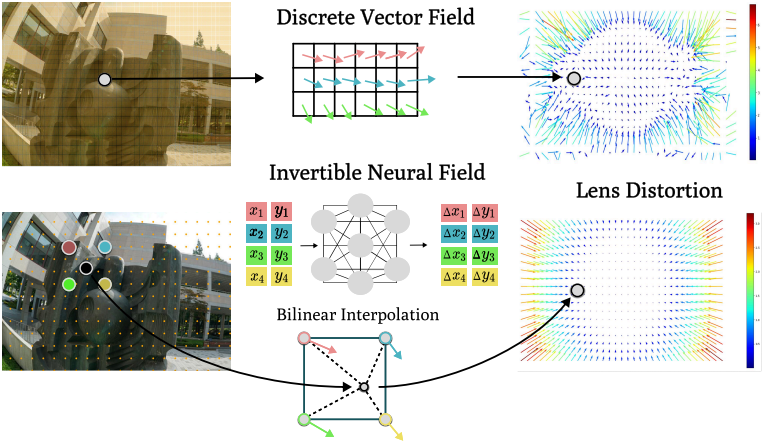
일반적인 카메라 모델을 구현하는 가장 간단한 방법은 픽셀 좌표 그리드에서 렌즈 왜곡을 명시적으로 최적화하고 bilinear interpolation을 적용하여 연속적인 distortion field를 추출하는 것이다.

\[\begin{equation} \mathcal{D}_\theta (\textbf{x}) = \textbf{x} + \textrm{interp}(\textbf{x}, \theta), \quad \textrm{interp}(\textbf{x}, \theta) = W(\textbf{x}, \theta) \cdot \theta \end{equation}\]

($\theta \in \mathbb{R}^{H \times W \times 3}$는 최적화 가능한 파라미터로 구성된 2D 벡터 그리드, $W$는 bilinear interpolation 가중치)

이러한 그리드 기반 방법은 $W$가 sparse하고 그리드 해상도를 높이면 더 복잡한 함수를 모델링할 수 있으므로 표현력이 풍부하고 효율적이다. 그러나 그리드 기반 방법은 렌즈 왜곡을 제대로 모델링하는 데 필요한 부드러움이 부족하여 overfitting으로 이어진다.

Invertible Residual Networks

렌즈 왜곡을 모델링하는 또 다른 방법은 적절한 inductive bias를 가진 신경망을 사용하는 것이다. NeuroLens는 비선형 렌즈 왜곡을 표현하기 위해 invertible ResNet을 사용할 것을 제안하였다. 구체적으로, deformation mapping은 residual network로 모델링된다.

\[\begin{equation} \mathcal{D}_\theta (\textbf{x}) = F_L \circ \cdots \circ F_1 (\textbf{x}), \quad F_i (z) = z + f_{\theta_i}^{(i)} (z) \end{equation}\]

\(f_{\theta_i}^{(i)}\)는 립시츠 상수가 1로 제한되어 가역적인 residual block이다. 각 block은 linear layer 4개로 구현되며, 본 논문에서는 $L = 5$개의 block을 사용했다.

Invertible ResNet은 표현력과 정규화를 모두 제공하지만, 3DGS에 직접 적용하기에는 계산량이 너무 많다. 이미지를 렌더링할 때 알파 블렌딩 가중치로 gradient를 backpropagation하려면 \(\mathcal{D}_\theta\)의 backward pass들을 위한 계산 그래프가 각 Gaussian에 대해 유지되어야 한다. 이는 장면에 있는 3D Gaussian의 수가 수백만 개에 달하는 경우가 많아 메모리가 부족하기 때문에 불가능하다.

Hybrid Distortion Field

그리드 기반 방법은 효율적이지만 overfitting되는 경향이 있고, invertible ResNet은 적절한 inductive bias를 가지지만 효율적이지 않다. 본 논문에서는 두 방법의 장점을 결합한 하이브리드 방법을 제안하였다. 구체적으로, invertible ResNet \(\mathcal{R}_\theta\)를 사용하여 그리드에서 flow field를 예측하고, 각 projection된 2D Gaussian에 bilinear interpolation을 적용한다.

\[\begin{equation} \mathcal{D}_\theta (\textbf{x}) = \textbf{x} + \textrm{interp}(\textbf{x}, \mathcal{R}_\theta (\textbf{P}_c) - \textbf{P}_c) \end{equation}\]

(\(\textbf{P}_c \in \mathbb{R}^{H \times W \times 2}\)는 고정된 제어점의 그리드, $H \times W$는 이미지 해상도가 아닌 제어점의 해상도)

이러한 아키텍처의 장점은 비용이 많이 드는 ResNet 계산이 그리드 해상도에 비례하고 장면 내 Gaussian 개수와 무관하다는 것이다. 각 Gaussian에 대해 필요한 추가 연산은 \(\textrm{interp}(\cdot)\)이며, 이는 계산 부담이 적고 병렬 처리가 가능하다.

2. Cubemap for Large FOV

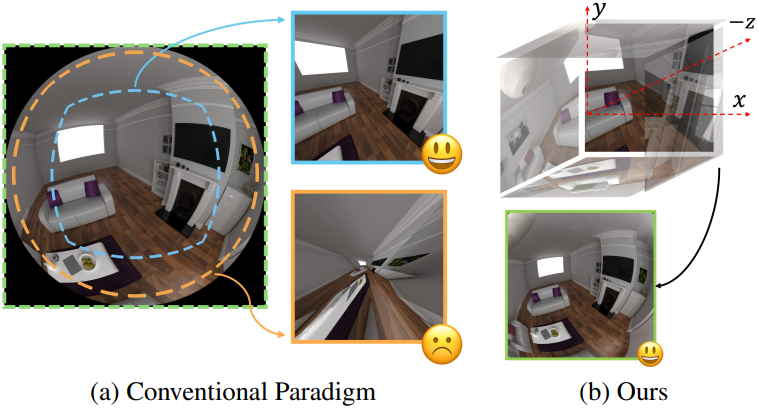
더 넓은 FOV를 가진 카메라에 본 방법을 적용하기 위해, 저자들은 단일 평면 projection 방식을 cubemap projection 방식으로 확장했다. 수학적으로, 단일 평면 projection 방식은 주변부 영역에서 업샘플링을 필요로 하며, FOV가 180°에 가까워질수록 샘플링 속도가 급격히 증가한다. 반면, cubemap을 이용한 렌더링은 이미지 중심에서 가장자리까지 비교적 균일한 픽셀 밀도를 유지하므로 광각 렌더링에 이상적이다.

Single-Planar Projection

기존 방법은 SfM에서 추정된 파라미터를 사용하여 원본 이미지를 perspective 이미지로 reprojection한다. 이렇게 reprojection된 이미지는 NeRF 또는 3DGS와 같은 perspective 기반 파이프라인을 통해 재구성하는 데 사용된다. 그러나 이 과정에서 주변 영역의 픽셀이 늘어나며, 이미지가 더 큰 FOV로 reprojection될수록 그 효과가 더욱 두드러진다. Reprojection된 FOV가 110°일 때 (파랑색) 업샘플링률은 약 1.4이지만, FOV가 170°로 증가하면 (주황색) 이 비율은 11.4로 증가하여 재구성에 필요한 고주파 정보의 상당 부분을 불가피하게 희생하게 된다.

또한, 중심부의 디테일을 보존하기 위해서는 보정된 이미지의 해상도가 더 높아야 한다. 원본 이미지 중심부의 픽셀 밀도가 보정된 이미지의 픽셀 밀도와 이상적으로 일치해야 하기 때문이다. 일반적인 해결책은 COLMAP의 방법처럼 주변부를 잘라내는 것이지만, 이는 광각 정보를 캡처하기 위해 fisheye 렌즈 카메라를 사용하는 의도와 상반된다.

Multi-Planar Projections

본 논문에서는 90°의 FOV를 커버하고 서로 직교하는 cubemap projection을 이용하여 초광각 렌더링을 표현하는 방식을 제안하였다. Cubemap 면을 따라 리샘플링함으로써 180°보다 큰 FOV에서도 왜곡된 이미지를 렌더링할 수 있다. 먼저 rasterization을 통해 cubemap의 각 면을 얻는다. 렌더링된 각 픽셀에 대해, 생성된 cubemap에서 해당 위치를 찾는다. 그런 다음, hybrid distortion field가 리샘플링하여 왜곡된 렌더링을 구현한다. 실제로는 카메라 렌즈의 FOV에 따라 cubemap 면의 개수가 달라질 수 있으므로, cubemap의 모든 면을 한 번에 렌더링할 필요는 없다.

리샘플링 단계는 hybrid distortion field와 함께 간단한 좌표 변환만을 포함한다. 공유 카메라 중심에서 각 평면까지의 거리는 1로 정규화된다. 예를 들어, 90° FOV 외부의 픽셀 $(x, y)$을 렌더링하려면 ($x > 1$, $\vert y \vert < 1$), 오른쪽 면의 픽셀은 오른쪽을 바라보는 카메라 좌표계에서 $(-\frac{1}{x}, \frac{y}{x})$로 얻을 수 있다. 렌즈 왜곡 \((x^\prime, y^\prime) = \mathcal{D}_\theta (x, y)\)을 고려하면, 오른쪽 면의 조회 위치가 $(-\frac{1}{x^\prime}, \frac{y^\prime}{x^\prime})$으로 변경된다. 이렇게 전체 distortion field를 cubemap에 직접 적용하여 넓은 FOV 렌더링을 수행할 수 있다.

Gaussian Sorting

3DGS는 알파 블렌딩 전에 Gaussian들을 이미지 평면에 대한 orthogonal projection 거리를 기준으로 정렬한다. 그러나 cubemap 표현 방식에서는 Gaussian이 두 면 사이의 경계를 넘나들 수 있어, cubemap 전체에 걸쳐 정렬 순서가 일관되지 않은 여러 개의 projection이 발생할 수 있다. 이러한 불일치는 경계면에서 불연속성을 유발한다.

이 문제를 해결하기 위해, 기존의 정렬 방식을 카메라 중심에서부터의 거리를 기준으로 Gaussian을 정렬하는 거리 기반 접근 방식으로 대체한다. 이를 통해 모든 cubemap 면에서 rasterization 순서가 일관되게 유지되어 불연속성이 완화된다. 3DGS에서 사용된 affine 근사 때문에, cubemap 면 경계 부근의 Gaussian의 2D 공분산은 최종 렌더링에 약간의 영향을 미친다.

3. Optimization of Camera Parameters

본 파이프라인은 모든 카메라 파라미터를 미분한다. 저자들은 extrinsic 파라미터와 intrinsic 파라미터를 포함한 모든 카메라 파라미터에 대한 gradient를 이론적으로 도출하여, 카메라 모듈을 완벽하게 미분 가능하게 하고 왜곡 모델링과 함께 최적화할 수 있도록 하였다. 모든 gradient 계산은 CUDA 커널을 사용하여 구현되었다.

Experiments

1. Comparisons to Traditional Lens Models

다음은 FisheyeNeRF 데이터셋에 대한 비교 결과이다.

다음은 Fisheye-GS와의 비교 예시들이다.

다음은 실제 이미지에 왜곡을 적용한 다음 비교한 예시이다.

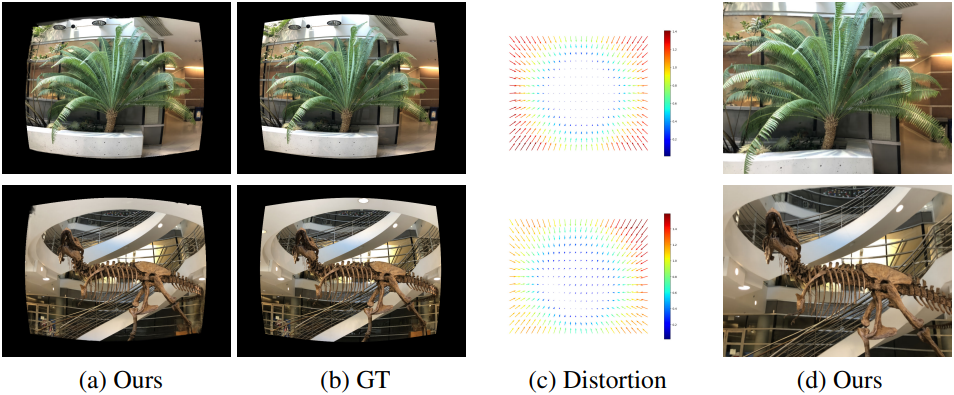
2. Large FOV Reconstruction with Few Captures

다음은 Mitsuba 장면에 대한 평가 결과이다.

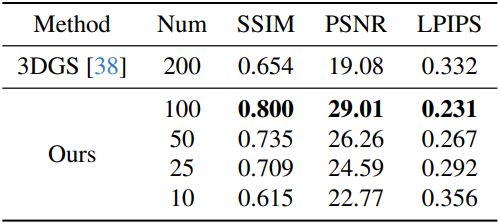
다음은 COLMAP을 사용한 3DGS와의 렌더링 결과를 비교한 예시들이다.

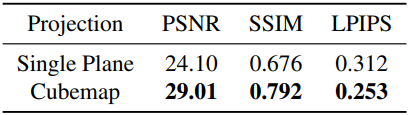
3. Ablation Studies

다음은 (왼쪽) hybrid distortion field와 (오른쪽) cubemap에 대한 ablation 결과이다.