[논문리뷰] SegMASt3R: Geometry Grounded Segment Matching
ICCV 2025 Spotlight. [Paper] [Page]
Rohit Jayanti, Swayam Agrawal, Vansh Garg, Siddharth Tourani, Muhammad Haris Khan, Sourav Garg, Madhava Krishna
IIIT Hyderabad | Heidelberg University | MBZUAI
6 Oct 2025
Introduction
Segment matching은 baseline이 넓은 경우에 급격히 저하된다. 이는 동일한 장면의 이미지가 크게 분리된 시점에서 촬영되어 원근감, 크기, 그리고 최대 180° 회전 변화가 발생하는 경우이다. DINOv2 또는 ViT와 같은 사전 학습된 인코더의 feature에 의존하는 기존 접근 방식은 반복적인 패턴을 불일치시키거나 동일한 물체에 대한 매우 다른 시점을 연결하지 못하는 경우가 많다.
본 논문에서는 3D foundation model인 MASt3R의 강력한 공간적 inductive bias를 활용하여 baseline이 넓은 경우에 대한 segment matching 문제를 해결하는 방안을 제안하였다. 공간적 추론에 대한 inductive bias는 baseline이 넓은 segment matching 문제와 같이 기하학적 일관성이 필요한 응용 분야에 매우 적합하다.
저자들은 패치 레벨의 임베딩을 segment 레벨의 descriptor로 변환하는 가벼운 segment-feature head를 추가하여 segment matching에 MASt3R를 적용했다. 이미지 쌍이 주어지면, 이러한 descriptor들을 매칭하여 segment correspondence를 구축한다. Head는 SuperGlue를 따르는 contrastive objective를 사용하여 학습된다.
본 논문의 모델인 SegMASt3R는 훨씬 더 큰 데이터셋과 SOTA local feature matching 방법을 사용하여 학습된 SAM2의 video propagator를 포함한 강력한 모델들을 능가하는 것으로 나타났다.
Method
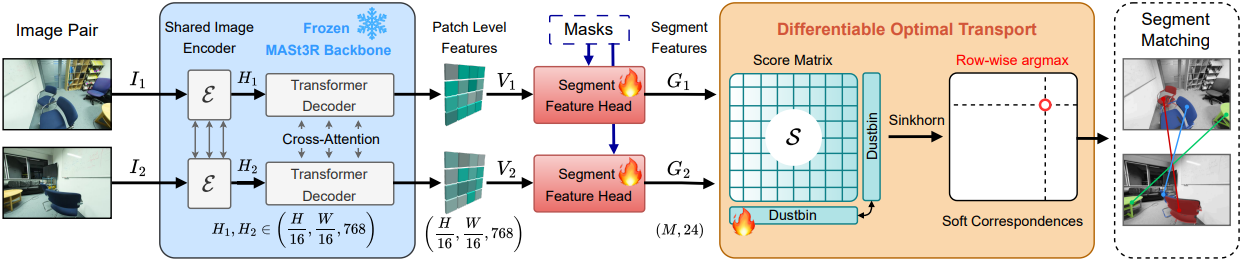
1. Segment-Feature Head: Segment-Aligned Features
MASt3R는 먼저 2개의 이미지 $I_1$과 $I_2$를 하나의 ViT 인코더 $\mathcal{E}$에 각각 입력하여 feature 세트 $H_1$과 $H_2$를 얻는다. 그런 다음, CroCo 스타일의 transformer 디코더로 두 feature 세트를 공동으로 개선한다.
\[\begin{equation} \textbf{H}_1 = \mathcal{E}(I_1), \quad \textbf{H}_2 = \mathcal{E}(I_2) \\ (\textbf{V}_1, \textbf{V}_2) = \textrm{Decoder} (\textbf{H}_1, \textbf{H}_2) \end{equation}\]$V_1$과 $V_2$의 크기는 $(\frac{H}{16} \times \frac{W}{16} \times 768)$이다. 원래 MASt3R에서 feature head는 \(\textbf{V}_1\)과 \(\textbf{V}_2\)를 입력 이미지의 해상도로 업샘플링한다. 저자들은 segment matching을 위해 패치 수준 feature를 $M$개의 segment feature로 변환하는 또 다른 head를 도입하였다. 이 head는 패치 수준 feature \(\textbf{V}_1\)과 \(\textbf{V}_2\)를 이미지 해상도로 업샘플링하여 크기 $(H, W, 24)$의 feature map \(\textbf{P}_1\)과 \(\textbf{P}_2\)를 생성하는 MLP로 구현되며, 여기서 24는 feature 차원이다. 이 head를 segment-feature head라고 한다. Segment-feature head는 SAM2와 같은 segmentation 모델 또는 GT 주석에서 얻은 각 이미지에 대한 $M_1$, $M_2$개의 segment mask \(\textbf{M}_1\), \(\textbf{M}_2\)를 입력으로 사용한다. 마스크와 feature map은 모두 공간 차원을 따라 flatten된다.
\[\begin{equation} \textbf{P}_\textrm{flat} \in \mathbb{R}^{24 \times HW}, \quad \textbf{M}_\textrm{flat} \in \mathbb{R}^{M \times HW} \end{equation}\]Pixel descriptor에서 segment descriptor로 전환하려면 행렬 곱셈을 통해 각 마스크 내부의 pixel descriptor를 집계한다.
\[\begin{equation} \textbf{G} = \textbf{M}_\textrm{flat} \textbf{P}_\textrm{flat}^\top \in \mathbb{R}^{M \times 24} \end{equation}\]두 이미지에 대한 결과 segment 임베딩 \(\textbf{G}_1\)과 \(\textbf{G}_2\)는 미분 가능한 matching layer에 입력된다. Batch 처리의 상한값으로 $M = 100$을 사용한다. 실제 이미지에는 GT 주석으로 학습할 때 일반적으로 20~30개의 마스크가 포함된다. 마스크가 더 적으면 0으로 채운다. Inference 시점에 마스크 개수는 학습 시점의 $M$ 값과 관계없이 임의로 설정할 수 있다.
2. Differentiable Segment Matching Layer
Cosine–similarity affinity
먼저 간단한 내적을 사용하여 affinity matrix \(\textbf{S} \in \mathbb{R}^{M_1 \times M_2}\)를 구성한다.
\[\begin{equation} S_{ij} = \langle \textbf{g}_i^1, \textbf{g}_j^2 \rangle, \quad 1 \le i \le M_1, \; 1 \le j \le M_2 \end{equation}\](\(\textbf{g}_i^1\)와 \(\textbf{g}_j^2\)는 각각 \(\textbf{G}_1\)과 \(\textbf{G}_2\)의 segment-level feature)
이상적으로는 동일한 3D 영역에 해당하는 segment feature는 높은 유사도 점수를 가져야 하고, 유사하지 않은 영역은 그에 상응하게 낮은 점수를 가져야 한다.
Learnable dustbin
SuperGlue를 따라, 대응 관계가 없는 segment를 처리하기 위해 affinity matrix $\textbf{S}$에 dustbin row와 dustbin column을 통합한다. 이는 baseline이 넓은 매칭에 필수적이다. 학습 가능한 logit $\alpha \in \mathbb{R}$로 초기화된 추가 행과 열을 연결하여 $\tilde{\textbf{S}}$가 생성된다.
\[\begin{equation} \tilde{\textbf{S}} = \begin{bmatrix} \textbf{S} & \alpha \textbf{1}_{M_1} \\ \alpha \textbf{1}_{M_2} & \alpha \end{bmatrix} \in \mathbb{R}^{(M_1 + 1) \times (M_2 + 1)} \end{equation}\]Soft Correspondences via Sinkhorn
유사도 logit은 log-space에서 Sinkhorn normalisation을 $T$번 반복하여 soft assignment matrix $\textbf{P}$로 변환된다.
\[\begin{aligned} \textbf{P}^{(0)} & \leftarrow \exp (\tilde{\textbf{S}} / \tau) \\ u_i^{(t)} &= \frac{1}{\sum_j P_{ij}^{(t)}}, \quad v_j^{(t)} = \frac{1}{\sum_i P_{ij}^{(t)}} \\ P_{ij}^{(t+1)} &= u_i^{(t)} P_{ij}^{(t)} v_j^{(t)}, \quad 0 \le t < T \end{aligned}\]($\tau$는 temperature hyperparameter)
수렴 후, $\textbf{P} = \textbf{P}^{(T)}$는 거의 bi-stochastic matrix이다.
\[\begin{equation} \sum_i P_{ij} \approx 1, \quad \sum_j P_{ij} \approx 1 \end{equation}\]최종 매칭 결과를 얻으려면 dustbin column이 아닌 열에 대해 간단한 행별 argmax 연산을 수행하면 된다.
3. Supervision
저자들은 SuperGlue의 cross-entropy loss \(\mathcal{L}_\textrm{SG}\)를 채택하였다.
\[\begin{equation} \mathcal{L} = -\sum_{(i,j) \in \mathcal{M}} \log P_{ij} - \sum_{i \in \mathcal{U}_1} \log P_{i, M_2 + 1} - \sum_{j \in \mathcal{U}_2} \log P_{M_1 + 1, j} \end{equation}\]($\mathcal{M}$은 GT match, \(\mathcal{U}_1\)과 \(\mathcal{U}_2\)는 각각 이미지 1과 2의 일치하지 않는 인덱스)
$\alpha$는 네트워크의 나머지 부분과 공동으로 학습되므로, matching layer는 불일치 선언에 따른 비용과 일치 신뢰도 간의 균형을 맞출 수 있다. 이러한 완전 미분 가능한 설계를 통해 matching layer는 end-to-end로 학습이 가능하다.
Experiments
- 데이터셋: ScanNet++
- 학습 디테일
- optimizer: AdamW
- learning rate: $10^{-4}$에서 $10^{-6}$으로 cosine annealing
- weight decay: $10^{-4}$
- batch size: 36
- epoch: 20
- segment-feature head는 MASt3R의 local feature head의 가중치로 초기화
- $\alpha$는 1.0으로 초기화
- Sinkhorn iteration: 50
- GPU: NVIDIA RTX A6000 1개로 22시간 소요
1. Segment Matching
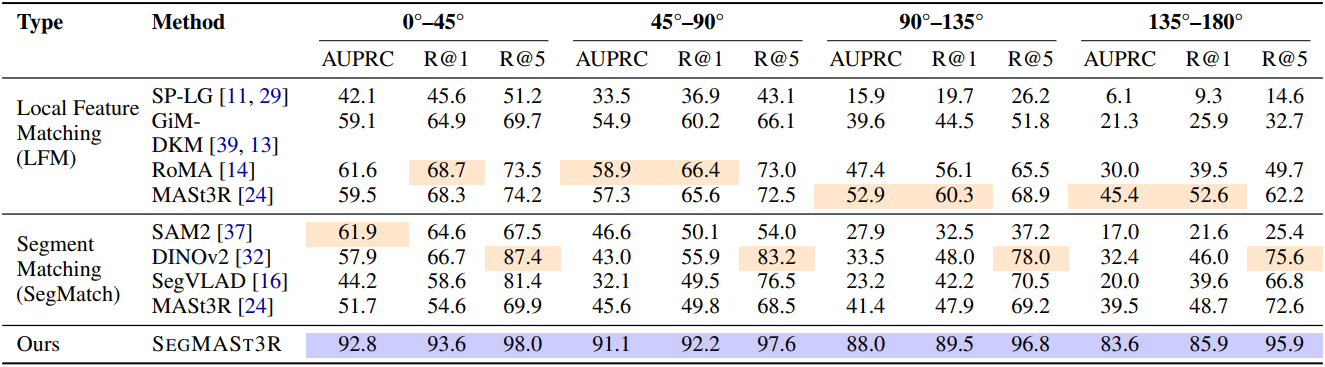
다음은 ScanNet++ 데이터셋에서 매칭 성능을 비교한 결과이다.

다음은 Replica 데이터셋에서 매칭 성능을 비교한 결과이다.

다음은 MapFree 데이터셋에서 매칭 성능을 비교한 결과이다.


2. 3D Instance Mapping
다음은 instance mapping 성능을 비교한 결과이다. (Replica)

3. Noisy Segmentation Masks
다음은 FastSAM의 마스크를 사용하였을 때의 성능을 비교한 결과이다. (ScanNet++)

4. Object-level Topological Navigation
다음은 내비게이션 성능을 비교한 결과이다.


5. Ablation Study
다음은 feature 인코더에 대한 영향을 비교한 결과이다. (ScanNet++)
