[논문리뷰] SEGA: Instructing Text-to-Image Models using Semantic Guidance

NeurIPS 2023. [Paper] [Diffusers]
Manuel Brack, Felix Friedrich, Dominik Hintersdorf, Lukas Struppek, Patrick Schramowski, Kristian Kersting
German Research Center for Artificial Intelligence | TU Darmstadt | Hessian.AI | LAION
28 Jan 2023

Introduction

Text-to-image diffusion model의 최근 인기는 주로 다양성, 표현력, 그리고 가장 중요하게는 사용자에게 제공하는 직관적인 인터페이스에 기인한다. 생성의 의도는 자연어로 쉽게 표현될 수 있으며 모델은 텍스트 프롬프트에 대한 충실한 해석을 생성한다. 이러한 모델의 뛰어난 능력에도 불구하고 처음에 생성된 이미지의 품질이 좋은 경우는 거의 없다. 따라서 사용자는 초기 이미지의 특정 측면에 만족하지 않을 가능성이 높으며 여러 번의 반복을 통해 개선하려고 시도한다. 불행하게도 입력 프롬프트의 작은 변화가 완전히 다른 이미지로 이어지기 때문에 diffusion process는 다소 취약하다. 결과적으로 생성 프로세스에 대한 세밀한 semantic 제어가 필요하며, 이는 초기 생성만큼 사용하기 쉽고 다양해야 한다.

생성 프로세스 중에 전용 개념에 영향을 미치려는 이전 시도들은 추가 segmentation mask, 아키텍처 확장, 모델 fine-tuning, 또는 임베딩 최적화가 필요했다. 이러한 기술들은 만족스러운 결과를 생성하지만 애초에 diffusion model의 장점인 빠르고 탐색적인 작업을 방해하다. 본 논문은 모델에 내재된 semantic 방향을 발견하고 상호 작용하기 위해 Semantic Guidance (SEGA)을 제안하였다. SEGA는 추가 학습, 아키텍처 확장, 외부 guidance가 필요하지 않으며 하나의 forward pass 내에서 계산된다. 즉 모델의 noise 추정만을 사용하여 간단한 텍스트 설명에서 이 semantic 제어를 추론할 수 있다. 이를 통해 저자들은 이러한 noise 추정치들이 semantic 제어에 적합하지 않다고 주장하는 이전 연구들을 반박한다. SEGA를 통해 밝혀진 guidance 방향은 강력하고 단조롭게 확장되며 대부분 격리되어 있다. 이를 통해 이미지에 대한 미묘한 편집, 합성 및 스타일 변경, 예술적 개념 최적화를 동시에 적용할 수 있다. 또한 SEGA를 사용하면 diffusion model의 latent space를 조사하여 추상적 개념이 모델에 의해 어떻게 표현되고 그 해석이 생성된 이미지에 어떻게 반영되는지에 대한 통찰력을 얻을 수 있다. 또한 SEGA는 아키텍처에 구애받지 않으며 latent 및 픽셀 기반 diffusion model을 포함한 다양한 생성 모델과 호환된다.

Semantic Guidance

1. Guided Diffusion

SEGA를 향한 첫 번째 단계는 guided diffusion이다. 특히, diffusion model은 Gaussian 분포 변수의 noise를 반복적으로 제거하여 학습된 데이터 분포의 샘플을 생성한다. Text-to-image 생성을 위해 모델은 텍스트 프롬프트 $p$로 컨디셔닝되고 해당 프롬프트에 충실한 이미지를 향해 가이드된다. Diffusion model \(\hat{\mathbf{x}}_\theta\)의 목적 함수는 다음과 같이 쓸 수 있다.

\[\begin{equation} \mathbb{E}_{\mathbf{x}, \mathbf{c}_p, \epsilon, t} [w_t \| \hat{\mathbf{x}}_\theta (\alpha_t \mathbf{x} + \omega_t \epsilon, \mathbf{c}_p) - \mathbf{x} \|_2^2] \end{equation}\]

여기서 \((\mathbf{x}, \mathbf{c}_p)\)는 텍스트 프롬프트 $p$로 컨디셔닝된다. $t$는 균일 분포 $t \sim \mathcal{U}([0,1])$에서 샘플링되며, $\epsilon$은 Gaussian $\epsilon \sim \mathcal{N} (0, \mathbf{I})$에서 샘플링된다. $w_t$, $\omega_t$, $\alpha_t$는 $t$에 따라 이미지 충실도에 영향을 준다. 결과적으로 diffusion model은 \(\mathbf{z}_t := \mathbf{x} + \epsilon\)을 denoise하여 squared error loss로 $\mathbf{x}$를 생성하도록 학습된다. Inference 시, diffusion model은 \((\mathbf{z}_t − \tilde{\epsilon}_\theta)\)의 예측을 사용하여 샘플링된다.

Classifier-free guidance는 순수 생성 diffusion model을 사용하는 컨디셔닝 방법으로 사전 학습된 추가 classifier가 필요하지 않다. 학습 중에 텍스트 컨디셔닝 \(\mathbf{c}_p\)는 고정된 확률로 무작위로 제거되므로 unconditional 목적 함수와 conditional 목적 함수에 대한 결합 모델이 생성된다. Inference 중에 $\mathbf{x}$-예측에 대한 score 추정치는 guidance scale $s_g$를 사용하여 다음과 같이 조정된다.

\[\begin{equation} \tilde{\epsilon}_\theta (\mathbf{z}_t, \mathbf{c}_p) := \epsilon_\theta (\mathbf{z}_t) + s_g (\epsilon_\theta (\mathbf{z}_t, \mathbf{c}_p) - \epsilon_\theta (\mathbf{z}_t)) \end{equation}\]

직관적으로, unconditional한 $\epsilon$-예측은 조건부 예측의 방향으로 밀리고 $s_g$는 조정 범위를 결정한다.

2. Semantic Guidance on Concepts

저자들은 여러 방향으로 diffusion process에 영향을 미치기 위해 SEGA를 도입하였다. 이를 위해 모델의 latent space에 이미 존재하는 개념과만 상호 작용함으로써 classifier-free guidance에 도입된 원칙을 실질적으로 확장한다. 따라서 SEGA에는 추가 학습, 아키텍처 확장, 외부 guidance가 필요하지 않다. 대신 기존 diffusion iteration 중에 계산된다. 보다 구체적으로 SEGA는 텍스트 프롬프트 $p$ 외에도 생성된 이미지의 주어진 개념을 나타내는 여러 텍스트 설명 $e_i$를 사용한다.

SEGA의 전반적인 아이디어는 위 그림과 같이 고차원 $\epsilon$-space의 2D 추상화를 사용하여 가장 잘 설명된다. 직관적으로 공간은 semantic 개념을 나타내는 임의의 subspace의 합성으로 이해할 수 있다. 왕의 이미지를 생성하는 예시를 생각해보자. unconditional한 noise 추정(검은색 점)은 semantic grounding $\epsilon$-space의 임의의 지점에서 시작된다. “왕의 초상화”라는 프롬프트에 해당하는 guidance는 남성과 왕족의 개념이 중첩되는 $\epsilon$-space의 일부로 이동시켜 왕의 이미지로 이어지는 벡터(청색 벡터)를 의미한다. 이제 SEGA를 사용하여 생성 프로세스를 추가로 조작할 수 있다. Unconditional한 시작점에서 각 프롬프트에 따라 컨디셔닝된 추정치를 사용하여 ‘남성’과 ‘여성’(주황색/녹색 선)의 방향을 얻는다. 이 추론된 ‘남성’ 방향을 프롬프트 guidance에서 빼고 ‘여성’ 방향을 추가하면 이제 ‘왕실’과 ‘여성’ subspace의 교차점에 있는 $\epsilon$-space의 한 지점인 ‘여왕’에 도달한다. 이 벡터는 semantic guidance에 따른 최종 방향(빨간색 벡터)을 나타낸다.

Diffusion에서 semantic 격리

다음으로 저자들은 Stable Diffusion(SD)의 예시를 통해 diffusion model의 실제 noise 추정치의 공간을 조사하였다. 이를 통해 해당 공간 내에서 semantic 개념을 추출하고 이미지 생성 중에 적용할 수 있다.

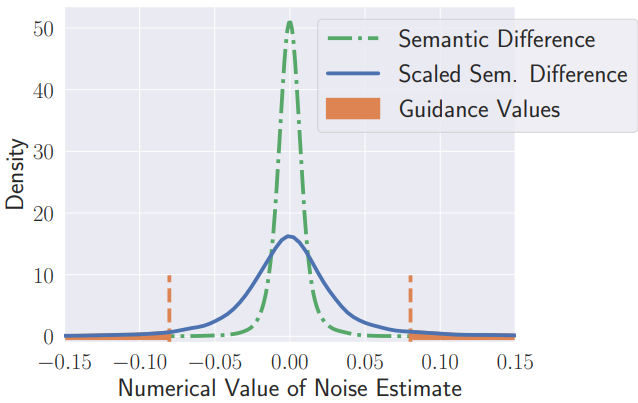
$\epsilon$-추정치의 수치는 일반적으로 가우시안 분포를 따른다. Latent 벡터의 각 차원 값은 시드, 텍스트 프롬프트, diffusion step에 따라 크게 다를 수 있지만 전체 분포는 항상 가우시안 분포와 유사하게 유지된다. Classifier-free guidance의 산술 원리를 사용하여 이제 임의의 semantic 개념을 인코딩하는 latent 벡터의 차원을 식별할 수 있다. 이를 위해 개념 설명 $e$로 컨디셔닝된 noise 추정치 \(\epsilon_\theta (\mathbf{z}_t, \mathbf{c}_e)\)를 계산한다. 그런 다음 \(\epsilon_\theta (\mathbf{z}_t, \mathbf{c}_e)\)와 unconditional score 추정치 \(\epsilon_\theta (\mathbf{z}_t)\)의 차이를 가져와 크기를 조정한다. 결과 latent 벡터의 수치 값은 위 그림에 표시된 것처럼 가우시안 분포이다. 분포의 위쪽 및 아래쪽 꼬리에 속하는 latent 차원만이 타겟 개념을 인코딩한다. 저자들은 $\epsilon$-추정치의 1~5%만 사용하면 이미지에 원하는 변경 사항을 적용하기에 충분하다는 것을 경험적으로 판단했다. 결과적으로 결과 개념 벡터는 대체로 격리된다. 따라서 여러 가지를 간섭 없이 동시에 적용할 수 있다. 이러한 sparse한 noise 추정 벡터의 공간을 semantic space라고 부른다.

하나의 방향

하나의 방향, 즉 편집 프롬프트부터 시작하여 SEGA의 직관을 공식적으로 정의해 보자. 세 가지 $\epsilon$-예측을 사용한다. 편집 방향에 따라 unconditional score 추정치 \(\epsilon_\theta (\mathbf{z}_t)\)를 프롬프트 조건부 추정치 \(\epsilon_\theta (\mathbf{z}_t, \mathbf{c}_p)\) 쪽으로 이동하고 동시에 개념 조건부 추정치 \(\epsilon_\theta (\mathbf{z}_t, \mathbf{c}_e)\)를 향해 쪽으로 이동하거나 멀어진다.

\[\begin{equation} \tilde{\epsilon}_\theta (\mathbf{z}_t, \mathbf{c}_p, \mathbf{c}_e) = \epsilon_\theta (\mathbf{z}_t) + s_g (\epsilon_\theta (\mathbf{z}_t, \mathbf{c}_p) - \epsilon_\theta (\mathbf{z}_t)) + \gamma (\mathbf{z}_t, \mathbf{c}_e) \end{equation}\]

여기서 semantic guidance 항 $\gamma$는 다음과 같다.

\[\begin{equation} \gamma (\mathbf{z}_t, \mathbf{c}_e) = \mu (\psi; s_e, \lambda) \psi (\mathbf{z}_t, \mathbf{c}_e) \end{equation}\]

여기서 $\mu$는 편집 guidance scale $s_e$를 element-wise하게 적용하고 $\psi$는 다음과 같이 편집 방향에 따라 달라진다.

\[\begin{equation} \psi (\mathbf{z}_t, \mathbf{c}_e) = \begin{cases} \epsilon_\theta (\mathbf{z}_t, \mathbf{c}_e) - \epsilon_\theta (\mathbf{z}_t) & \quad \textrm{if pos. guidance} \\ -(\epsilon_\theta (\mathbf{z}_t, \mathbf{c}_e) - \epsilon_\theta (\mathbf{z}_t)) & \quad \textrm{if neg. guidance} \end{cases} \end{equation}\]

따라서 guidance 방향 변경은 \(\epsilon_\theta (\mathbf{z}_t, \mathbf{c}_e)\)와 \(\epsilon_\theta (\mathbf{z}_t)\) 사이의 방향에 의해 반영된다.

$\mu$는 정의된 편집 프롬프트 $e$와 관련된 프롬프트 조건부 추정치의 차원을 고려하여야 한다. 이를 위해 $\mu$는 unconditional한 추정치와 개념 조건부 추정치 간의 차이의 가장 큰 절대값을 취한다. 이는 백분위수 threshold $\lambda$로 정의된 수치적 분포의 위쪽 및 아래쪽 꼬리에 해당한다. 꼬리의 모든 값은 편집 scaling factor $s_e$에 의해 조정되고 다른 모든 값은 0으로 설정된다.

\[\begin{equation} \mu (\psi; s_e, \lambda) = \begin{cases} s_e & \quad \textrm{where} \vert \psi \vert \ge \eta_\lambda (\vert \psi \vert) \\ 0 & \quad \textrm{otherwise} \end{cases} \end{equation}\]

여기서 \(\eta_\lambda (\psi)\)는 $\psi$의 $\lambda$번째 백분위수이다. 결과적으로 $s_e$가 클수록 SEGA의 효과가 증가한다.

SEGA는 diffusion model의 수학적 배경에서 이론적으로 동기를 부여받을 수도 있다. Classifier-free guidance 항이 없는 양의 방향에 대한 격리된 semantic guidance 방정식은 다음과 같이 쓸 수 있다.

\[\begin{equation} \bar{\epsilon}_\theta (\mathbf{z}_t, \mathbf{c}_e) \approx \epsilon_\theta (\mathbf{z}_t) + \mu (\epsilon_\theta (\mathbf{z}_t, \mathbf{c}_e) - \epsilon_\theta (\mathbf{z}_t)) \end{equation}\]

또한, \(p(\textbf{c}_e \vert \textbf{z}_t) \propto p(\textbf{z}_t \vert \textbf{c}_e) / p(\textbf{z}_t)\)인 implicit classifier를 가정해 보자. \(p(\textbf{z}_t \vert \textbf{c}_e)\)의 정확한 추정값 \(\epsilon^\ast (\textbf{z}_t, \textbf{c}_e)\)와 \(p(\textbf{z}_t)\)의 정확한 추정값 \(\epsilon^\ast (\textbf{z}_t)\)를 가정하면 결과 classifier의 기울기는 다음과 같이 쓸 수 있다.

\[\begin{equation} \nabla_{\textbf{z}_t} \log p (\textbf{c}_e \vert \textbf{z}_t) = - \frac{1}{\omega_t} (\epsilon^\ast (\textbf{z}_t, \textbf{c}_e) - \epsilon^\ast (\textbf{c}_e)) \end{equation}\]

Classifier guidance를 위해 이 implicit classifier를 사용하면 다음과 같이 noise 추정치가 생성된다.

\[\begin{equation} \bar{\epsilon^\ast} (\textbf{z}_t, \textbf{c}_e) = \epsilon^\ast (\textbf{z}_t) + w (\epsilon^\ast (\textbf{z}_t, \textbf{c}_e) - \epsilon^\ast (\textbf{z}_t)) \end{equation}\]

이는 가장 큰 절대값을 갖는 classifier 신호의 차원을 분리하는 $\mu$를 갖는 SEGA와 기본적으로 유사하다. 그러나 \(\bar{\epsilon^\ast} (\textbf{z}_t, \textbf{c}_e)\)는 ̀\(\bar{\epsilon}_\theta (\textbf{z}_t, \textbf{c}_e)\)와 근본적으로 다르다. \((\textbf{z}_t, \textbf{c}_e)\)는 classifier의 기울기가 아니라 제약이 없는 네트워크의 출력이기 때문이다. 결과적으로 SEGA의 성능에 대한 보장은 없다. 그럼에도 불구하고 이 유도는 견고한 이론적 토대를 마련했으며 SEGA의 효과를 경험적으로 입증할 수 있다.

Diffusion process에 대한 더 많은 제어를 제공하기 위해 위에 제시된 방법론에 두 가지 조정을 적용한다. Diffusion process에서 초기 warm-up 이후 guidance $\gamma$를 적용할 warm-up 파라미터 $\delta$를 추가한다. 즉, $t < \delta$인 경우 \(\gamma (\textbf{z}_t, \textbf{c}_e) := 0\)이다. 당연히 $\delta$ 값이 높을수록 생성된 이미지의 실질적인 조정이 덜해진다. 전체 이미지 구성을 변경하지 않고 유지하려는 경우 충분히 높은 $\delta$를 선택하면 세밀한 디테일만 변경할 수 있다.

또한, 동일한 방향으로 지속적으로 가이드되는 차원에 대한 timestep에 대한 guidance를 가속화하기 위해 semantic guidance $\gamma$에 momentum 항 $\nu_t$를 추가한다. 따라서 $\gamma_t$는 다음과 같이 정의된다.

\[\begin{equation} \gamma (\textbf{z}_t, \textbf{c}_e) = \mu (\psi; s_e, \lambda) \psi (\textbf{z}_t, \textbf{c}_e) + s_m \nu_t \end{equation}\]

여기서 $s_m \in [0,1]$은 momentum scale이며, $\nu$는 다음과 같이 업데이트된다.

\[\begin{equation} \nu_{t+1} = \beta_m \nu_t + (1 - \beta_m) \gamma_t \end{equation}\]

여기서 $\nu_0 = \textbf{0}$이고 $\beta_m \in [0, 1)$이다. 따라서 $\beta_m$이 클수록 momentum의 변동성이 덜해진다. Warm-up에서 $\gamma_t$가 적용되지 않더라도 momentum은 warm-up 동안 이미 구축된다.

한 방향의 넘어

이제 여러 개념 $e_i$를 향한 단 하나의 방향을 사용하는 것 이상으로 나아가서 $\gamma_t$의 여러 계산을 결합할 수 있다.

모든 $e_i$에 대해 위에서 설명한 대로 $\gamma_t^i$를 계산하고 각각 고유한 hyperparameter 값 $\lambda^i$, $s_e^i$를 정의한다. 모든 $\gamma_t^i$의 가중 합은 다음과 같다.

\[\begin{equation} \hat{\gamma}_t (\textbf{z}_t, \textbf{c}_e) = \sum_{i \in I} g_i \gamma_t^i (\textbf{z}_t, \textbf{c}_{e_i}) \end{equation}\]

다양한 warm-up을 다루기 위해 $t < \delta_i$인 경우 $g_i$는 $g_i = 0$으로 정의된다. 그러나 momentum은 모든 편집 프롬프트를 사용하여 구축되고 모든 warm-up이 완료되면 적용된다.

SEGA의 기본 방법론은 아키텍처에 구애받지 않으며 classifier-free guidance를 사용하는 모든 모델에 적용 가능하다. 결과적으로 다양한 아키텍처의 다양한 생성 모델에 대해 SEGA를 사용할 수 있다.

Properties of Semantic Space

Robustness

SEGA는 임의의 개념을 원본 이미지에 통합하기 위해 robust하게 작동한다. 위 그림은 다양한 도메인의 이미지에 ‘안경’ 개념에 대한 guidance를 적용한 것이다. 특히, 이 프롬프트는 안경을 주어진 이미지에 통합하는 방법에 대한 어떠한 맥락도 제공하지 않으므로 해석의 여지를 남긴다. 묘사된 예시는 SEGA가 대상 개념의 최선의 통합을 의미론적으로 기반이 되는 원본 이미지로 추출하는 방법을 보여준다. 이는 SEGA의 사용을 쉽게 만들고 초기 이미지 생성과 동일한 탐색 특성을 제공한다.

Uniqueness

한 개념의 guidance 벡터 $\gamma$는 고유하므로 한 번 계산한 후 다른 이미지에 적용할 수 있다. 위 그림은 가장 왼쪽 이미지에서 ‘안경’에 대한 semantic guidance를 계산하고 다른 프롬프트의 diffusion process에서 벡터를 간단히 추가한 예시이다. 모든 이미지는 각각의 $\epsilon$-추정치가 필요 없이 안경을 착용하도록 생성된다. 이는 포토리얼리즘에서 드로잉으로의 전환에서 볼 수 있듯이 상당한 도메인 전환도 포함한다.

그러나 $\epsilon$-추정치는 발산하는 초기 noise latent에 따라 크게 변경되므로 전송은 동일한 초기 랜덤시드로 제한된다. 또한 사람의 얼굴에서 동물 또는 무생물에 이르기까지 이미지 합성에 대한 보다 광범위한 변경에는 별도의 guidance 벡터 계산이 필요하다. 그럼에도 불구하고 SEGA는 결과 이미지에 눈에 띄는 아티팩트를 발생시키지 않는다.

Monotonicity

이미지의 semantic 개념의 크기는 semantic guidance 벡터의 강도에 따라 단조롭게 확장된다. 위 그림은 semantic guidance $s_e$의 강도에 따른 효과를 보여준다. Positive guidance와 negative guidance 모두에서 scale의 변화는 미소나 찡그림의 강도와 관련이 있다. 결과적으로, 생성된 이미지에 대한 모든 변경 사항은 semantic guidance scale $s_e$와 warm-up $\delta$만 사용하여 직관적으로 조정될 수 있다. 생성 프로세스에 대한 이러한 제어 수준은 원하는 개념별 편집 강도를 임의로 조합하여 여러 개념에 적용할 수도 있다.

Isolation

각 개념 벡터에는 총 noise 추정치의 일부만 필요하기 때문에 다양한 개념이 크게 분리된다. 즉, 서로 다른 벡터가 서로 간섭하지 않는다. 따라서 위 그림과 같이 동일한 이미지에 여러 개념을 동시에 적용할 수 있다. 예를 들어, 먼저 추가된 안경은 나중에 추가된 편집 내용에도 변경되지 않고 그대로 유지되는 것을 볼 수 있다. 이를 활용하여 여러 개념을 사용하여 가장 잘 표현되는 보다 복잡한 변경을 수행할 수 있다. 예를 들어 ‘남성’ 개념을 제거하고 ‘여성’ 개념을 추가하여 성별을 바꿀 수 있다.

Experimental Evaluation

Empirical Results

다음은 10가지 얼굴 속성에 대한 이미지 변환 예시들이다.

다음은 얼굴 속성에 대한 user study 결과이다.

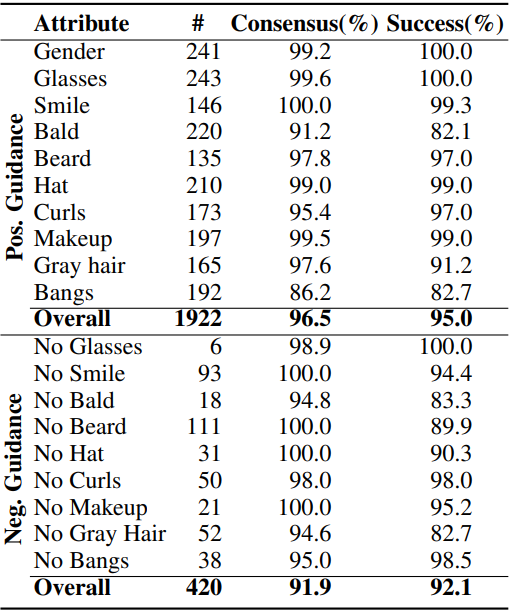
다음은 얼굴 속성 동시 조합에 대한 user study 결과이다.

다음은 Inappropriate Image Prompts (I2P) 벤치마크에 대한 결과이다.

Comparisons

다음은 user study를 통해 다양한 방법들과 성공률을 비교한 표이다.

Qualitative Results

다음은 SEGA에 대한 정량적 결과들이다.