Diffusion은 신이고 GPT는 무적이다

arXiv 2022. [Paper]
Wenbo Li, Xin Yu, Kun Zhou, Yibing Song, Zhe Lin, Jiaya Jia
The Chinese University of Hong Kong | The University of Hong Kong | Tencent AI Lab | Adobe Inc
6 Dec 2022

Introduction

GAN은 inpainting에서 성공을 거두었지만 학습이 불안정하고 복잡한 분포를 학습하는 데 어려움을 겪는다. 특히 고품질 이미지의 넓은 영역을 inpainting하는 데 어려움을 겪는다. 반대로, autoregressive (AR) model과 diffusion model과 같은 반복적인 알고리즘은 학습이 더 안정적이고 더 잘 수렴한다. AR model은 이미지를 픽셀 단위로 처리하므로 고해상도 데이터를 다루기 어렵다. 반면, diffusion model은 좋은 추정을 달성하기 위해서는 수 천번의 반복이 필요하다. 따라서 inpainting에서 이러한 방법들을 직접 사용하면 각각의 단점이 발생한다.

본 논문에서는 넓은 영역의 inpainting을 위해 새로운 spatial diffusion model (SDM)을 개발하였다. SDM은 반복적인 방법으로 inpainting을 수행하며, 모든 픽셀이 각 iteration에서 병렬로 예측되고 적합한 픽셀만 다음 iteration을 위해 유지된다. 신뢰할 수 있는 픽셀을 알려지지 않은 위치로 점진적으로 확산시키는 과정으로 작용한다. 저자들의 핵심 디자인은 GAN의 효율적인 최적화와 확률 모델의 tractable한 장점을 활용하는 간단하면서도 매우 효과적인 분리된 확률 모델링에 있다.

디테일하게 보면 모델은 inpainting 결과 (평균 항)와 불확실성 맵 (분산 항)을 동시에 예측한다. 평균 항은 implicit한 적대적 학습으로 최적화되어 적은 반복으로 더 정확한 예측이 가능하다. 분산 항은 반대로 explicit하게 가우시안 정규화로 모델링된다.

이 분리된 전략은 다양한 장점이 있다.

  1. 적대적 최적화 덕분에 반복하는 step의 수가 크게 줄어든다.
  2. 가우시안 정규화에서 산출된 분산 항은 자연스럽게 불확실성 척도 역할을 하여 신뢰할 수 있는 추정치를 선택할 수 있게 한다.
  3. Explicit한 모델링은 지속적인 샘플링을 가능하게 하여 품질과 다양성이 향상된 예측으로 이어진다.
  4. 불확실성 측정은 신경망이 효율적인 추론을 위해 더 유익한 픽셀을 활용하도록 장려하는 uncertainty-guided attention mechanism을 구축하는 데 도움이 돤다.

Our Method

본 논문의 목표는 누락된 부분이 많은 마스킹된 이미지를 사실적으로 완성하는 것이다. 먼저 포괄적인 분석과 함께 spatial diffusion model(SDM)을 공식화한다. 그 다음에 모델 디자인과 손실 함수에 대한 디테일이 이어진다.

1. Spatial Diffusion Model

GAN 기반 방법은 기존 방법보다 훨씬 더 나은 결과를 달성하지만 여전히 넓은 누락 영역을 처리하는 데 큰 어려움이 있다. 그 이유 중 하나를 GAN의 one-shot 특성에 두고 대신 반복적인 inpainting을 제안한다.

각 pass에 필연적으로 좋은 예측이 있기 때문에 이러한 픽셀을 다음 세대를 위한 단서로 사용한다. 이러한 방식으로 SDM은 가치있는 정보를 전체 이미지에 점진적으로 전파한다.

1.1 Decoupled Probabilistic Modeling

반복적인 inpainting을 위하여 예측의 정확도를 평가하기 위한 메커니즘을 찾아야 한다. 직관적인 해결책 중 하나는 tractable한 확률 모델을 도입하여 불확실성 정보를 수치적으로 계산하는 것이다. 하지만, 이는 종종 근사화된 타겟 분포가 가우시안 분포라는 가정으로 이어지며, 이는 복잡한 분포를 설명하기에는 너무 간단하다. DDPM과 같은 여러 반복 모델이 주변 분포의 표현을 풍부하게 하지만 일반적으로 높은 inference 비용이 필요하다.

본 논문은 이 문제를 해결하기 위하여 효율적인 반복 inpainting을 위한 분리된 확률 모델을 제안한다. Implicit한 GAN 기반의 최적화와 explicit한 가우시안 정규화의 장점을 분리된 방법으로 모두 활용한다. 따라서 정확한 예측과 explicit한 불확실성 측정을 동시에 얻을 수 있다.


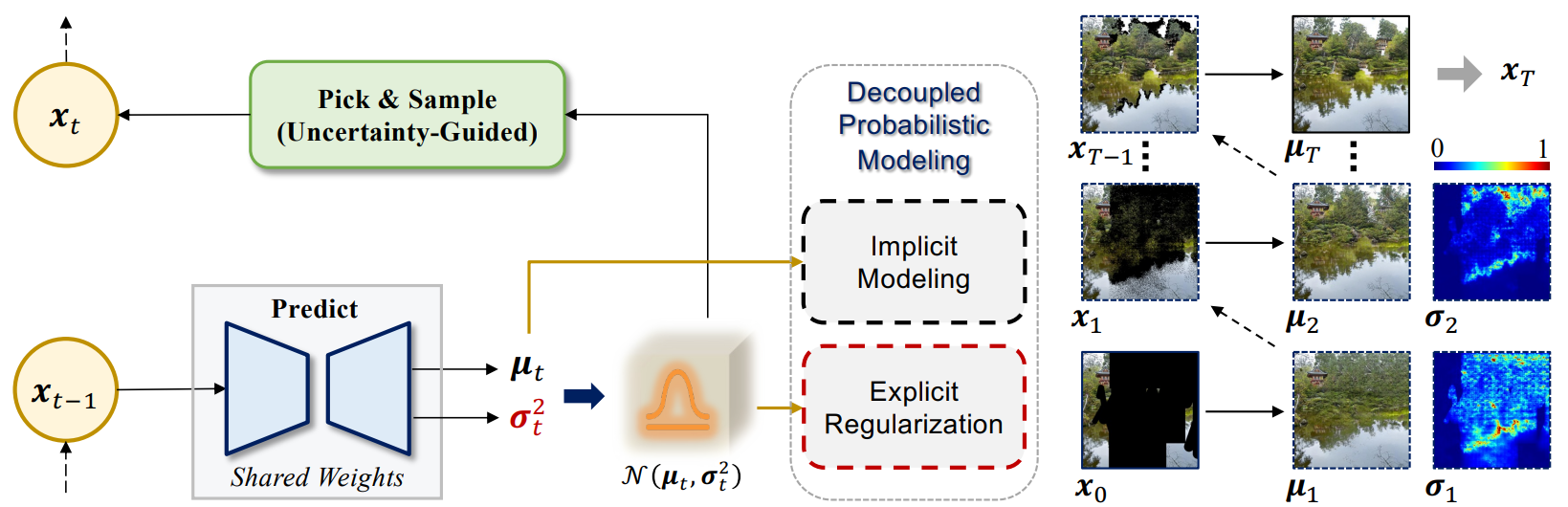
위 그림과 같이 입력 이미지 $x_t$가 주어지면 본 논문의 모델은 inpainting 결과 $\mu_t$와 불확실성 맵 $\sigma_t^2$을 예측한다. Adversarial loss를 사용하여 $\mu_t$를 supervise하며, ($\mu_t$, $\sigma_t^2$)를 가우시안 분포의 평균과 분산으로 취급한다. GAN의 implicit한 최적화는 실제 분포를 최대한 가깝게 근사하도록 만들며, iteration의 수를 대단히 줄일 수 있다. 모델은 평균 항을 위해 explicit한 불확실성을 측정하여 신뢰할 수 있는 픽셀들을 고를 수 있도록 한다. 가우시안 정규화는 주로 negative log likelihood (NLL) \(\mathcal{L}_{nll}\)를 사용하여 분산 항에 적용된다.

\[\begin{equation} \mathcal{L}_{nll} = -\sum_{i=1}^D \log \int_{\delta_{-} (y^i)}^{\delta_{+} (y^i)} \mathcal{N} (y; \textrm{sg}[\mu_\theta^i (x)], \sigma_\theta^i (x)^2) dy \end{equation}\]

$D$는 데이터의 차원이고 $i$는 픽셀 인덱스이다. 입력 $x$와 출력 $y$는 [-1, 1]로 스케일링되고 $\delta_{-} (y)$와 $\delta_{+} (y)$는 다음과 같다.

\[\begin{aligned} \delta_{+} (y) &= \begin{cases} \infty & \textrm{if} \; y = 1 \\ y + \frac{1}{255} & \textrm{if} \; y < 1 \\ \end{cases} \\ \delta_{-} (y) &= \begin{cases} -\infty & \textrm{if} \; y = -1 \\ y - \frac{1}{255} & \textrm{if} \; y > -1 \\ \end{cases} \end{aligned}\]

Stop-gradient 연산 $\textrm{sg}[\cdot]$을 사용하면 가우시안 제약이 분산 항만 최적화시켜 더 정확한 평균 항이 추정된다고 한다.

1.2 Spatial Diffusion Scheme

Feed-forward network $f_\theta (\cdot)$을 사용하여 알려진 영역에서 정보를 주는 픽셀을 전체 이미지로 점진적으로 확산시킨다.

\[\begin{equation} x_t, m_t, u_t = f_\theta (x_{t-1}, m_{t-1}, u_{t-1}) \end{equation}\]

$x_t$는 마스킹된 이미지, $m_t$는 이진 마스크, $u_t$는 불확실성 맵이다. 신경망의 파라미터는 모든 iteration에서 공유된다.

저자들은 여러 iteration을 사용하여 성능을 개선시킨다. 본 논문의 방법은 $t$번째 iteration에서 아래와 같이 실행된다.

  1. Predict. $x_{t-1}$, $m_{t-1}$, $u_{t-1}$이 주어지면 평균 $\mu_t$와 분산 $\sigma_t^2$이 모든 픽셀에 대하여 추정된다. 그런 다음 [0, 1]로 스케일링된 예비 불확실성 맵 $\tilde{u}_t$가 분산 맵을 변환하여 생성된다.
  2. Pick. 먼저 모르는 픽셀들에 대한 불확실성 점수를 정렬한다. 사전 정의된 mask schedule에 따라 이 iteration에서 추가할 픽셀 수를 계산하고, 불확실성이 가장 낮은 픽셀들을 알려진 픽셀 카테고리에 삽입하여 마스크를 $m_t$로 업데이트한다. 예비 불확실성 맵 $\tilde{u}_t$를 기반으로 아직 누락된 위치를 1로 표시하고 초기에 알려진 픽셀을 0으로 표시하여 최종 불확실성 맵 $u_t$를 얻는다.
  3. Sample. 두 가지 상황을 고려한다. 첫 번째는 $m_0$의 알려진 위치에 대하여 항상 원본 입력 픽셀 $x_0$를 사용하는 것이다. 두 번째는 inpainting 영역에 대해 $\mu_t$와 $\sigma_t$에 따라 연속 샘플링을 적용한다. 이 경우 아래의 수식을 사용한다. $\alpha$는 조절 가능한 비율이고 $z \sim \mathcal{N}(0,I)$이다. $\odot$은 Hadamard product이다. 마지막 iteration은 $\sigma_t z$ 항을 사용하지 않는다.
\[\begin{equation} x_t = x_0 + (m_t - m_0) \odot (\mu_t + \alpha \cdot \sigma_t \odot z) \end{equation}\]

2. Model Architecture

U-Net 아키텍처와 StyleGAN 디코더를 사용하여 넓은 receptive field에 도달하여 이미지의 컨텍스트 정보의 장점을 얻는다. 추가로 전역적인 상호 작용이 고해상도에서 훨씬 더 크고 다양한 데이터셋의 reconstruction 품질을 크게 향상시키므로 다양한 해상도에서 여러 attention block을 도입한다.

Feature의 유사성에만 기반하여 기존 attention mechanism은 픽셀이 정보를 교환할 수 있는 동등한 기회를 제공한다. 그러나 inpainting task의 경우, 누락된 픽셀은 지정된 동일한 값으로 초기화되어 서로 가깝게 만든다. 결과적으로 보이는 영역의 유용한 정보를 효과적으로 활용할 수 없으며, 설상가상으로 유효한 픽셀이 손상되어 콘텐츠가 흐릿하고 불만족스러운 아티팩트가 발생한다.


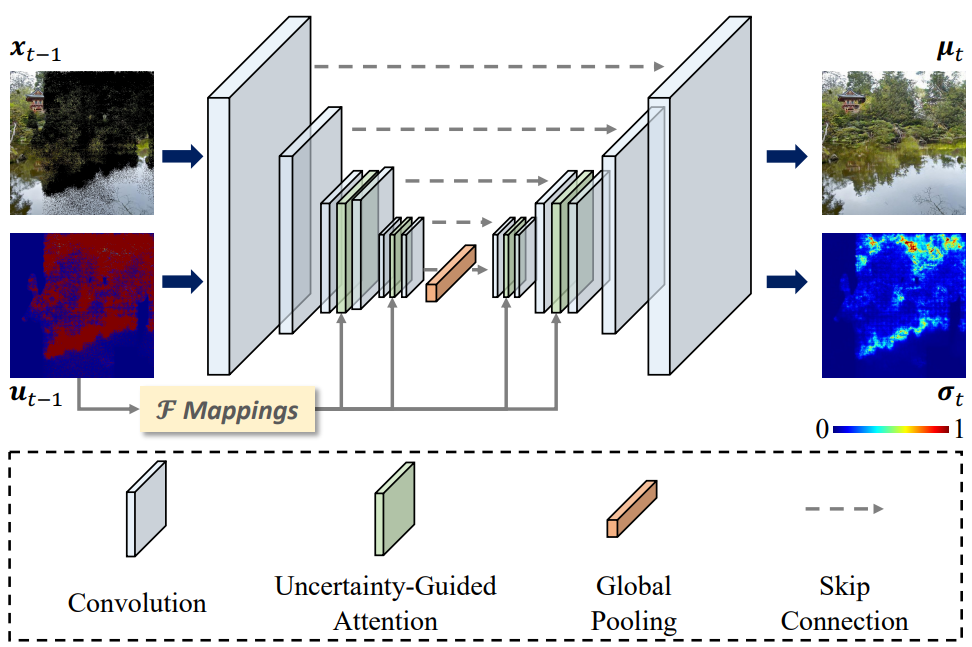
위 그림과 같이 본 논문은 aggregating weight를 조정하기 위해 픽셀의 불확실성 점수를 고려하여 위에서 언급한 문제를 제대로 해결한다. Attention 연산은 다음과 같이 계산된다.

\[\begin{equation} \textrm{Attention} (q, k, v, u) = \textrm{Softmax} \bigg( \frac{qk^T}{\sqrt{d_k}} + \mathcal{F} (u) \bigg) v \end{equation}\]

\(\{q, k, v\}\)는 query, key, value 행렬이고 $d_k$는 scaling factor이다. $\mathcal{F}$는 불확실성 맵 $u$를 기반으로 편향된 픽셀 가중치를 예측하고 reshape 연산을 포함하는 학습 가능한 함수이다.

3. Loss Functions

각 iteration에서 모델은 평균과 분산 추정치를 출력한다. 평균 항은 adversarial loss \(\mathcal{L}_{adv}\)와 perceptual loss $\mathcal{L}_{pcp}$를 사용하여 최적화되어 자연스러운 이미지를 생성하는 것을 목표로 한다.

Adversarial loss

\[\begin{aligned} \mathcal{L}_{ag} &= - \mathbb{E}_{\hat{x}} [\log (D(\hat{x}))] \\ \mathcal{L}_{ad} &= - \mathbb{E}_{\hat{x}} [\log (D(x))] - \mathbb{E}_{\hat{x}} [\log (1 - D(\hat{x}))] \end{aligned}\]

$x$는 실제 이미지이고 $\hat{x}$는 예측된 이미지이다.

Perceptual loss

\[\begin{equation} \mathcal{L}_{pcp} = \sum_i \| \phi_i (x) - \phi_i (\hat{x}) \|_2^2 \end{equation}\]

$\phi$는 사전 학습된 ResNet50의 layer output이다.

불확실성 모델링을 위하여 분산을 제약하는 negative log likelihood $\mathcal{L}_{nll}$을 적용한다. 따라서 generator의 전체 손실 함수는 다음과 같다.

\[\begin{equation} \mathcal{L} = \sum_j \lambda_1 \mathcal{L}_{ag}^j + \lambda_2 \mathcal{L}_{pcp}^j + \lambda_3 \mathcal{L}_{nll}^j \end{equation}\]

$j$는 diffusion iteration 수이다. 실험에서는 $\lambda_1 = 1$, $\lambda_2 = 2$, $\lambda_3 = 10^{-4}$로 설정한다.

Experiments

  • 데이터셋: 512$\times$512 해상도의 Places2와 CelebA-HQ
  • 평가 지표: FID, P-IDS, U-IDS
  • 구현 디테일
    • 인코더-디코더 아키텍처. 인코더는 여러 conv block, 디코더는 StyleGAN2의 디코더
    • 인코더의 채널 크기는 64에서 시작하여 downsampling마다 512까지 2배
    • 인코더와 디코더 모두 32$\times$32, 16$\times$16에서 attention block 적용
    • 첫 번째 iteration에서 불확실성 맵은 “1 - mask”로 초기화
    • Feature 크기는 32배 줄인 다음 복원
    • 학습에 exponential moving average (EMA), adaptive discriminator augmentation (ADA), weight modulation 사용
    • batch size 32, learning rate $10^{-3}$, Adam optimizer ($\beta_1 = 0$, $\beta_2 = 0.99$), $\alpha = 0.01$, 8 NVIDIA A100 GPU

1. Ablation Study

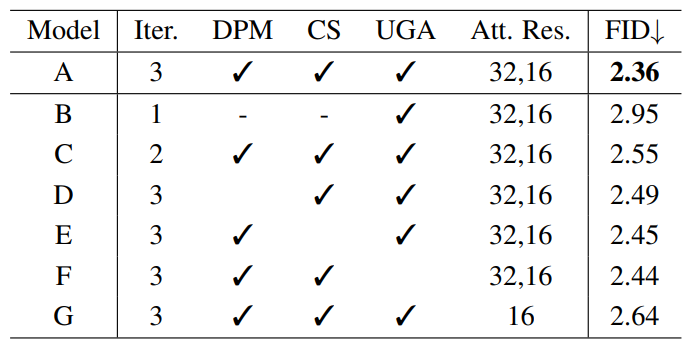
다음 표는 학습에서의 iteration 수, decoupled probabilistic modeling (DPM), continuous sampling (CS), uncertainty-guided attention (UGA)에 대한 ablation study 결과이다.

Iterative number

Ablation study 결과 표에서 볼 수 있듯 iteration 수가 감소하면 FID가 증가한다.

아래 그림은 iteration 수에 따른 샘플의 비교이다.


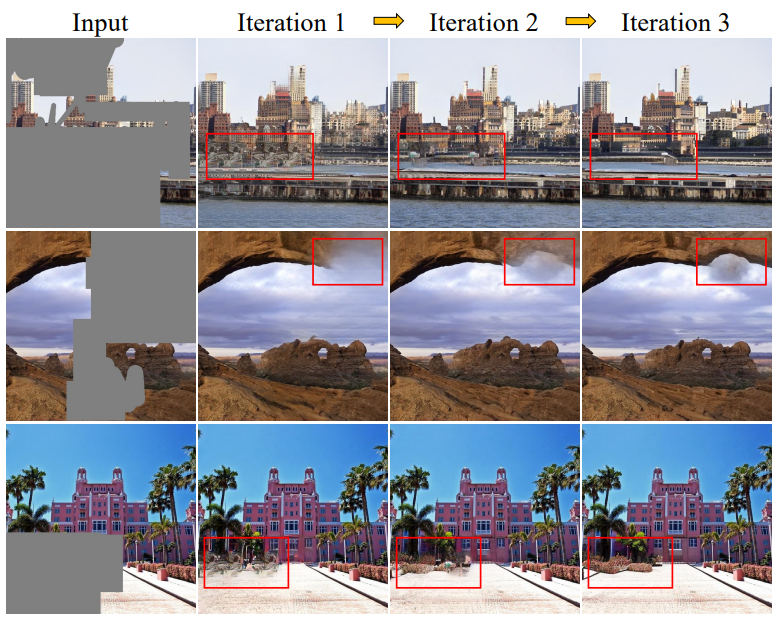
더 많은 iteration을 적용하면 더 심미적으로 만족스러운 컨텐츠를 생산할 수 있다.

다음 표는 테스트에서의 iteration 수에 따른 FID 변화를 보여준다.


모델 “A”와 “B”를 비교해보면 학습 과정보다 inference 단계의 iteration 수가 더 중요하다는 것을 알 수 있다.

Decoupled probabilistic modeling

Ablation study 결과 표를 보면 decoupled probabilistic modeling을 사용하지 않으면 FID가 증가함을 알 수 있다.

또한 아래 그림에서 모델 “D”가 흐릿한 컨텐츠를 생성하려는 경향이 있음을 알 수 있다.

Continuous sampling

Ablation study 결과 표를 보면 continuous sampling을 사용하지 않으면 FID가 증가함을 알 수 있다.

또한 아래 그림에서 모델 “E”보다 모델 “A”가 보이는 픽셀을 따라 더 잘 복구하는 것을 볼 수 있다.


아래 그림은 본 논문의 방법이 다양한 생성이 가능함을 보여주는 예시이다.


하지만, 평균 항이 낮은 불확실성으로 추정되거나 iteration 수가 제약되는 경우 결과의 차이가 항상 분명하지는 않다.

Uncertainty-guided attention

본 논문에서는 거리가 있는 컨텍스트를 충분히 활용하기 위해 attention block이 프레임워크에 추가되었다. 먼저 attention을 32$\times$32와 16$\times$16에 사용하는 경우 (모델 “A”)와 16$\times$16에만 사용하는 경우 (모델 “G”)를 비교하면 FID가 크게 증가하였다. 이는 넓은 범위의 상호 작용이 넓은 영역을 inpainting할 때 상당히 중요하다는 것을 의미한다.

모델 “A”와 uncertainty-guided attention 대신 기존 attention mechanism을 사용한 모델 “F”를 비교하면 작은 성능 하락을 보였다.

아래 그림을 보면 “F”의 경우 창분의 디테일이 떨어진다.

Mask schedule

다음 표는 다양한 mask schedule에 대한 FID를 보여준다.


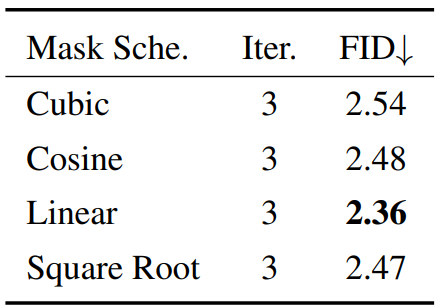
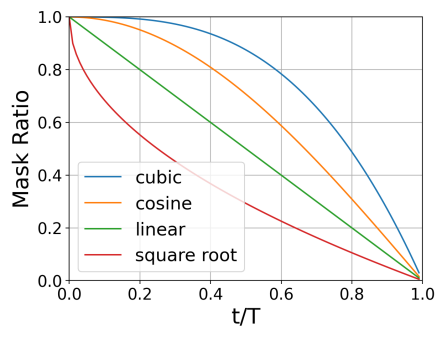
저자들은 입력 이미지의 마스크 비율이 광범위하므로 균일한 schedule을 사용할 때 더 안정적인 학습이 가능하다고 주장한다.

2. Comparisons to State-of-the-Art Methods

다음 표는 SDM을 다양한 GAN 기반 모델, AR 모델, diffusion model과 비교한 결과이다.


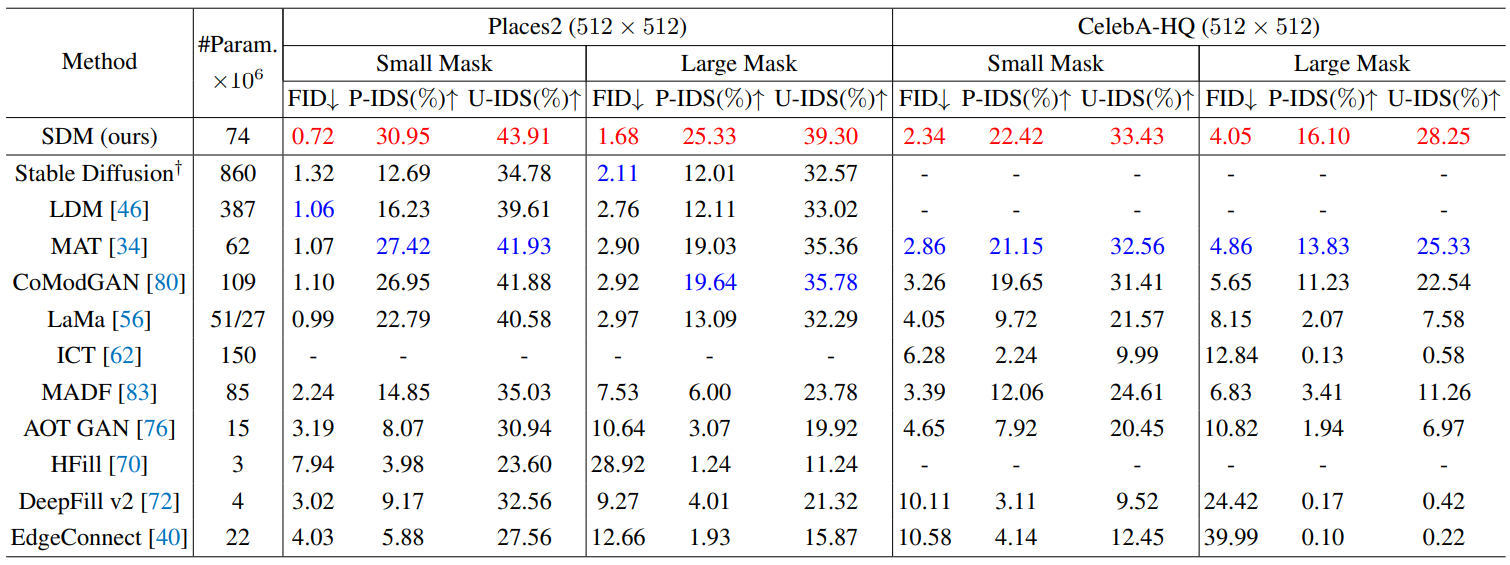
데이터셋의 종류와 마스크 크기에 상관 없이 SDM의 성능이 가장 우수하였다.

다음은 시각적 비교를 위한 그림이다.

You may also enjoy