[논문리뷰] Variational Diffusion Auto-encoder: Latent Space Extraction from Pre-trained Diffusion Models (ScoreVAE)
arXiv 2023. [Paper]
Georgios Batzolis, Jan Stanczuk, Carola-Bibiane Schönlieb
DAMTP, University of Cambridge
24 Apr 2023
Introduction
VAE (Variational Autoencoder)는 unsupervised learning을 위한 강력한 도구로 입증되어 복잡한 데이터 분포의 효율적인 모델링 및 생성을 가능하게 한다. 그러나 VAE에는 고차원 데이터의 기본 구조를 캡처하는 데 어려움이 있는 흐릿한 이미지를 생성하는 등 중요한 한계가 있다. 이러한 문제는 조건부 데이터 분포 $p(x \vert z)$가 가우시안 분포로 근사될 수 있다는 비현실적인 모델링 가정으로 인해 나타난다. 또한 $p(x \vert z)$에서 샘플링하는 대신 모델은 단순히 분포의 평균을 출력하므로 바람직하지 않은 smoothing 효과가 발생한다. 본 논문에서는 diffusion model의 능력을 활용하여 유연한 방식으로 $p(x \vert z)$를 모델링하여 이 가정을 완화할 것을 제안한다. 저자들은 $p(x \vert z)$를 모델링하는 인코더 네트워크가 $p(x)$에 대해 학습된 unconditional diffusion model과 쉽게 결합되어 $p(x \vert z)$에 대한 모델을 생성할 수 있음을 보여준다.
Diffusion model은 최근 데이터 분포 $p(x)$를 추정하기 위해 diffusion process의 역 과정을 사용하는 생성 모델링을 위한 유망한 기술로 부상했다. Diffusion model은 이미지 합성 및 오디오 생성과 같은 많은 task에서 SOTA 성능을 달성하는 복잡한 고차원 분포를 캡처하는 데 매우 성공적인 것으로 입증되었다. 최근 연구에서는 diffusion model이 복잡한 조건부 확률 분포를 효과적으로 캡처하고 이를 inpaiting, super-resolution, image-to-image translation과 같은 문제를 해결하는 데 적용할 수 있음을 보여주었다.
조건부 분포 학습에서 diffusion model의 성공에 힘입어 최근 연구들에서는 조건부 diffusion model을 $p(x \vert z)$를 학습하도록 하여 VAE 프레임워크에서 디코더로 적용하는 방법을 모색했다. 본 논문은 diffusion decoder가 구식임을 보여줌으로써 이 연구 라인을 개선한다. 대신 $p(x \vert z)$에 대한 모델을 얻기 위해 score function에 대한 베이즈 정리를 통해 unconditional diffusion model과 인코더를 결합할 수 있다. 이 접근 방식에는 몇 가지 중요한 이점이 있다.
- $p(x \vert z)$에 대한 비현실적인 가우시안 가정을 방지한다. 따라서 흐릿한 샘플 생성을 피해 원래 VAE에 비해 성능이 크게 향상된다.
- 사용된 diffusion model은 unconditional이기 때문에, 즉 latent factor에 의존하지 않기 때문에 기존의 강력한 사전 학습된 diffusion model을 활용하고 이를 모든 인코더 네트워크와 결합할 수 있다. 또한 인코더를 재학습할 필요 없이 더 나은 모델을 위해 diffusion 구성 요소를 항상 쉽게 교체할 수 있다. 이것은 주어진 인코더에 대해 특별히 학습되어야 하는 조건부 diffusion model을 사용하는 이전 접근 방식과 대조된다.
- Score function에 베이즈 정리를 사용하여 인코더 학습에서 prior 학습을 분리하고 학습 역학을 개선할 수 있다. 이를 통해 조건부 diffusion model에 기반한 접근 방식보다 우수한 성능을 달성할 수 있다.
또한 저자들은 이 프레임워크에서 인코더를 최적화하는 데 사용할 수 있는 데이터 likelihood $p(x)$에 대한 새로운 하한을 도출하였다.
Method
1. Problems with conventional VAEs
VAE는 조건부 데이터 분포 $p_\theta (x \vert z)$를 디코더 네트워크 $d_\theta$에 의해 학습된 평균 $\mu_\theta^x (z)$와 공분산 $\Sigma_\theta^x (z)$를 갖는 가우시안 분포로 모델링한다. 또한 실제로는 $\Sigma_\theta^x = I$라고 가정하는 경우가 많다. 이러한 가정 하에서 조건부 log-likelihood
\[\begin{equation} \ln p_\theta (x \vert z) = - \frac{\| z - \mu_\theta^x (z) \|_2^2}{2} + \frac{d}{2} \ln (2 \pi) \end{equation}\]를 최대화하는 것은 $L_2$ reconstruction error를 최소화하는 것과 같다. 이미지와 같은 특정 데이터 modality를 처리할 때 이 모델이 부적합한 몇 가지 이유가 있다.
- 분포 $p_\theta (x \vert z)$를 샘플링하는 대신, $p_\theta (x \vert z)$의 샘플은 noise가 많은 이미지처럼 보이므로 VAE는 단순히 평균 $\mu_\theta^x (z)$를 출력하므로 바람직하지 않은 smoothing과 흐릿한 샘플로 이어진다.
- VAE의 loss function은 픽셀 레벨 $L_2$ 오차와 동일하며, 이는 이미지에 대한 인간의 인식 및 의미 체계와 매우 일치하지 않는다.
2. Conditional Diffusion Models as decoders
위의 문제를 완화하고 $p_\theta (x \vert z)$에 대한 비현실적인 가우시안 가정을 방지하기 위해 조건부 diffusion model을 학습할 수 있다. 조건부 diffusion model $s_\theta (x_t, z, t)$는 목적 함수
\[\begin{equation} \frac{1}{2} \mathbb{E}_{t, x_0, z, x_t} [\lambda(t) \| \nabla_{x_t} \ln p(x_t \vert x_0) - s_\theta (x_t, z, t) \|_2^2] \\ t \sim \mathcal{U}(0,T), \quad x_0, z \sim p(x_0, z), \quad x_t \sim p(x_t \vert x_0) \end{equation}\]를 최소화하여 조건부 데이터 score $\nabla_{x_t} \ln p(x_t \vert z)$를 근사화하기 위해 인코더 네트워크 $e_\phi : x_0 \mapsto z$와 공동으로 학습된다. 이는 가우시안 가정을 피함으로써 원래의 오토인코더 프레임워크를 크게 개선하고 샘플이 흐릿해지는 문제를 완화한다. 그러나 정규화 계수 $\beta$가 매우 작은 경우에도 VAE로 학습될 때, 즉 KL 페널티 항이 도입될 때 이 프레임워크가 실패한다. 이 학습 방법을 DiffDecoder라고 한다.
3. Score VAE: Encoder with unconditional diffusion model as prior
본 논문에서는 score에 대한 베이즈 정리를 활용하고 $\nabla_{x_t} \ln p(x_t \vert z)$의 구조를 사용하여 위의 아이디어에 대한 추가 개발을 제안한다. 인코더 학습에서 prior 학습을 분리하고 학습 역학을 개선할 수 있다. Score에 대한 베이즈 정리에 따르면 다음과 같다.
\[\begin{equation} \nabla_{x_t} \ln p(x_t \vert z) = \nabla_{x_t} \ln p(z \vert x_t) + \nabla_{x_t} \ln p(x_t) \end{equation}\]이는 조건부 데이터 score $\nabla_{x_t} \ln p(x_t \vert z)$를 데이터 prior score $\nabla_{x_t} \ln p(x_t)$와 latent posterior score $\nabla_{x_t} \ln p(z \vert x_t)$로 분해할 수 있음을 의미한다. 데이터 prior score는 데이터 space에서 unconditional diffusion model $s_\theta (x_t, t)$로 근사할 수 있으므로 강력한 사전 학습된 diffusion model을 활용할 수 있다. Latent posterior score $\nabla_{x_t} \ln p(z \vert x_t)$는 인코더 네트워크 $e_\phi (x_t, t)$에 의해 근사화된다. 데이터 prior와 latent posterior score에 대한 모델이 있으면 이를 결합하여 조건부 데이터 score를 얻을 수 있다. 그런 다음 완전한 latent 변수 모델을 얻는다. 데이터 $x$는 인코더 네트워크를 사용하여 latent 표현 $z$로 인코딩될 수 있으며 조건부 데이터 score $\nabla_{x_t} \ln p(x_t \vert z)$를 사용하여 조건부 reverse process를 시뮬레이션하여 재구성할 수 있다.
이 방법은 $p (x \vert z)$에 대한 강력하고 유연한 모델을 갖는 이점을 유지하면서 조건부 diffusion 접근법에 비해 몇 가지 장점이 있다. 조건부 diffusion 케이스에서 score 모델 $s_\theta (x_t, z, t)$는 인코더 네트워크 $e_\phi$와 공동으로 학습되어야 한다. 게다가 $s_\theta (x_t, z, t)$는 implicit하게 두 분포를 학습해야 한다. 먼저 $e_\phi$가 $x$에 대한 정보를 $z$로 인코딩하는 방법을 이해하기 위해 $p(z \vert x)$를 근사화해야 하고, 두 번째로 현실적인 재구성을 보장하기 위해 prior $p(x)$를 모델링해야 한다. 본 논문의 접근 방식에서 이 두 task는 명확하게 분리되어 두 개의 개별 네트워크에 위임된다. 따라서 diffusion model은 인코더 분포를 다시 학습할 필요가 없다. 대신 prior 분포와 인코더 분포는 score function에 대한 베이즈 정리를 통해 결합된다.
또한 unconditional prior 모델 $s_\theta (x_t, t)$는 인코더와 독립적으로 먼저 학습될 수 있다. 그런 다음 prior 모델을 고정하고 인코더 네트워크만 학습한다. 이러한 방식으로 항상 한 번에 하나의 네트워크만 학습하므로 학습 역학이 향상된다. 또한 데이터 prior 네트워크는 인코더를 재학습할 필요 없이 항상 더 나은 모델로 교체할 수 있다.
4. Modeling the latent posterior score
Latent posterior score는 인코더 네트워크에 의해 유도된다. 먼저 VAE와 유사하게 $t = 0$에서 가우시안 parametric model을 적용한다.
\[\begin{equation} p_\phi (z \vert x_0) = \mathcal{N} (z; \mu_\phi^z (x_0), \sigma_\phi^z (x_0) I) \end{equation}\]여기서 $\mu_\phi^z (x_0)$, $\sigma_\phi^z (x_0)$는 인코더 네트워크의 출력이다. 이것은 $p(x_t \vert x_0)$와 함께 분포 $p_\phi (z \vert x_t)$를 결정한다.
\[\begin{equation} p_\phi (z \vert x_t) = \mathbb{E}_{x_0 \sim p(x_0 \vert x_t)} [p_\phi (z \vert x_0)] \end{equation}\]$p_t (x_0 \vert x_t)$에서 샘플링하려면 각 학습 step에서 reverse SDE를 여러 번 풀어야 하므로 위의 내용은 계산하기 어렵다. 따라서 위의 분포에 대한 변형 근사를 고려한다.
\[\begin{equation} q_{t, \phi} (z \vert x_t) = \mathcal{N} (z; \mu_\phi (x_t, t), \sigma_\phi (x_t, t)) \end{equation}\]그리고 $q_{t, \phi} (z \vert x_t) \approx p_t (z \vert x_t)$인 파라미터 $\phi$를 학습한다.
위의 family (집합의 집합) 선택은 다음 관찰에 의해 정당화된다.
- $p(z \vert x_0)$가 가우시안이므로 $t = 0$에서 실제 분포는 family에 속한다. 또한 작은 $t$에 대해 분포 $p_t (x_0 \vert x_t)$가 $x_0$ 주위에 매우 집중되어 있기 때문에 $p_\phi (z \vert x_t)$가 대략 가우시안임을 알 수 있다.
- $t = 1$에서 실제 분포는 family의 원소에 의해 잘 근사될 수 있다. Noisy한 샘플 $x_1$이 더 이상 $z$에 대한 정보를 포함하지 않기 때문에 $p_1 (z \vert x_1) \approx p(z)$이다. 그리고 KL loss로 학습하고 있기 때문에 $p(z)$는 대략 가우시안이 될 것이다.
마지막으로 자동 미분을 사용하여 latent posterior score $\nabla_{x_t} \ln p(z \vert x_t)$에 대한 모델인 $\nabla_{x_t} \ln q_{t, \phi} (z \vert x_t)$를 계산할 수 있다.
5. Encoder Training Objective
$s_\theta (x_t, t) \approx \nabla_{x_t} \ln p(x_t)$를 사전 학습된 unconditional diffusion model의 score function이라고 하자. 또한
\[\begin{equation} e_\phi : (x_t, t) \mapsto (\mu_\phi^z (x_t, t), \sigma_\phi^z (x_t, t) I) \end{equation}\]는
\[\begin{equation} q_{t, \phi} (z \vert x_t) = \mathcal{N} (z; \mu_\phi^z (x_t, t), \sigma_\phi^z (x_t, t) I) \\ \nabla_{x_t} \ln q_{t, \phi} (z \vert x_t) \approx \nabla_{x_t} \ln p(z \vert x_t) \end{equation}\]를 정의하는 인코더 네트워크라고 하자. Score function에 대한 베이즈 정리에 따라 조건부 데이터 score $\nabla_{x_t} \ln p(x_t \vert z)$의 근사는 다음과 같다.
\[\begin{equation} s_{\theta, \phi} (x_t, z, t) := s_\theta (x_t, t) + \nabla_{x_t} \ln q_{t, \phi} (z \vert x_t) \end{equation}\]Log-likelihood $\ln p_{\theta, \phi} (x)$를 최대화하여 인코더를 학습한다.
\[\begin{equation} \mathcal{L}_\beta (\phi) := \mathbb{E}_{x_0} \bigg[ \frac{1}{2} \mathbb{E}_{t, x_t, z} [g(t)^2 \| \nabla_{x_t} \ln p_t (x_t \vert x_0) - s_{\theta, \phi} (x_t, z, t) \|_2^2 ] + \beta D_\textrm{KL} (q_{0, \phi} \;\|\; p(z)) \bigg] \\ x_0 \sim p(x_0), \quad t \sim \mathcal{U}(0, T), \quad x_t \sim p_t (x_t \vert x_0), \quad z \sim q_{0, \phi} (z \vert x_t) \end{equation}\]이 학습 방법을 ScoreVAE라고 한다.
6. Correction of the variational error
인코더 $e_\phi$가 학습되면 ground-truth 디코딩 score $∇xt ln p(xt|z)$의 근사치는
\[\begin{equation} s_{\theta, \phi} (x_t, z, t) := s_\theta (x_t, t) + \nabla_{x_t} \ln q_{t, \phi} (z \vert x_t) \end{equation}\]이다. 완벽한 최적화의 경우에도 근사는 ground-truth 디코딩 score와 일치하지 않는다. 인코더를 학습한 후 나머지를 근사하는 보조 수정 모델을 학습시켜 근사 오차를 수정할 수 있다. 보다 구체적으로, 디코딩 score의 근사치를 다음과 같이 정의한다.
\[\begin{equation} s_{\theta, \phi} (x_t, z, t) := s_\theta (x_t, t) + \nabla_{x_t} \ln q_{t, \phi} (z \vert x_t) + c_\psi (x_t, z, t) \end{equation}\]이미 학습된 인코더와 이전 모델의 가중치를 고정한 후 동일한 목적 함수를 사용하여 보정 모델 $c_\psi$를 학습시킨다. 이 학습 방법을 ScoreVAE+라고 한다.
Experiment
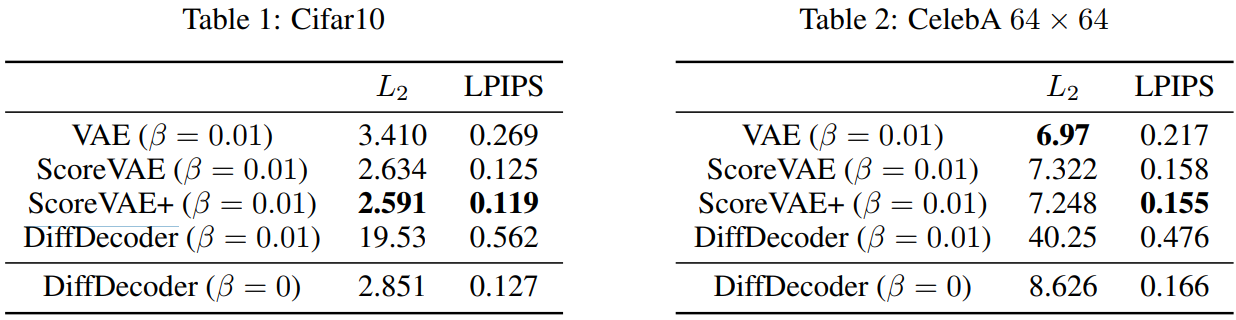
다음은 ScoreVAE와 ScoreVAE+를 $\beta$-VAE, DiffDecoder와 비교한 표이다.
다음은 CIFAR-10에서의 정성적 비교 결과이다.

다음은 CelebA 64$\times$64에서의 정성적 비교 결과이다.
