[논문리뷰] Simplifying, Stabilizing and Scaling Continuous-Time Consistency Models

ICLR 2025 (Oral). [Paper] [Page]
Cheng Lu, Yang Song
OpenAI
14 Oct 2024

Introduction

Consistency model (CM)은 diffusion model의 느린 샘플링 속도 문제를 해결하는 데 상당한 이점을 제공한다. 이전 연구들에서는 few-step 생성, 특히 1-step 또는 2-step 생성에서 효과가 입증되었다. 그러나 이러한 결과는 모두 discrete-time CM을 기반으로 하며, 이는 discretization 오차를 유발하고 timestep 그리드의 신중한 스케줄링을 요구하여 잠재적으로 최적이 아닌 샘플 품질로 이어질 수 있다. 이와 대조적으로 continuous-time CM은 이러한 문제를 피하지만 학습 불안정성이라는 문제에 직면했다.

본 논문에서는 continuous-time CM의 학습을 단순화, 안정화, 그리고 scaling하는 기법을 소개한다. 첫 번째 기여는 EDM과 flow matching을 통합하는 새로운 공식인 TrigFlow로, diffusion model, probability flow ODE, 그리고 CM의 공식을 크게 단순화한다. 이를 기반으로 CM 학습에서 불안정성의 근본 원인을 분석하고 이를 완화하기 위한 완벽한 방안을 제시하였다.

본 논문에서는 네트워크 아키텍처 내에서 시간 컨디셔닝과 adaptive group normalization을 개선하는 방안을 제시하였다. 또한, 안정적이고 scalable한 학습을 ​​위해 adaptive weighting과 normalization, 그리고 점진적 annealing을 통합하여 continuous-time CM의 학습 objective를 재구성하였다.

이러한 개선을 통해 consistency training과 consistency distillation 모두에서 CM의 성능을 향상시켜 기존의 discrete-time CM과 비교했을 때 동등하거나 더 나은 결과를 달성했다. 본 논문의 모델인 sCM은 다양한 데이터셋과 모델 크기에서 성공적인 결과를 보여주었다. 저자들은 CIFAR-10, ImageNet 64$\times$64, ImageNet 512$\times$512에서 sCM을 학습시켜 1.5B 파라미터의 전례 없는 규모에 도달했으며, 이는 현재까지 학습된 CM 중 가장 큰 규모이다. sCM은 연산량 증가에 따라 효과적으로 scaling되어 예측 가능한 방식으로 더 나은 샘플 품질을 달성하였다. 또한, 훨씬 더 많은 샘플링 연산을 필요로 하는 SOTA diffusion model과 비교했을 때, sCM은 2-step 생성을 사용하여 FID 차이를 10% 이내로 줄였다.

Preliminaries

Diffusion Model

Diffusion model은 데이터 샘플 \(\textbf{x}_0 \sim p_d\)에서 noisy한 버전 \(\textbf{x}_t = \alpha_t \textbf{x}_0 + \sigma_t \textbf{z}\)로 보내는 noising process의 반대 과정을 학습한다 ($\textbf{z} \sim \mathcal{N}(\textbf{0}, \textbf{I})$).

EDM

EDM의 objective는 다음과 같다.

\[\begin{equation} \mathbb{E}_{\textbf{x}_0, \textbf{z}, t} [w(t) \| \textbf{f}_\theta^\textrm{DM} (\textbf{x}_t, t) - \textbf{x}_0 \|_2^2] \\ \textrm{where} \quad \textbf{f}_\theta^\textrm{DM} (\textbf{x}_t, t) = c_\textrm{skip} (t) \textbf{x}_t + c_\textrm{out} (t) \textbf{F}_\theta (c_\textrm{in} (t) \textbf{x}_t, c_\textrm{noise}(t)) \end{equation}\]

($w(t)$는 weighting function)

EDM의 probability flow ODE (PF-ODE)는 다음과 같다.

\[\begin{equation} \frac{\textrm{d} \textbf{x}_t}{\textrm{d} t} = \frac{\textbf{x}_t - \textbf{f}_\theta^\textrm{DM}(\textbf{x}_t, t)}{t} \textrm{from} \; \textbf{x}_T \sim \mathcal{N}(\textbf{0}, T^2 \textbf{I}) \; \textrm{to} \; \textbf{x}_0 \end{equation}\]

Flow Matching

Flow matching의 objective는 다음과 같다.

\[\begin{equation} \mathbb{E}_{\textbf{x}_0, \textbf{z}, t} [w(t) \| \textbf{F}_\theta (\textbf{x}_t, t) - (\alpha_t^\prime \textbf{x}_0 + \sigma_t^\prime \textbf{z}) \|_2^2] \end{equation}\]

(일반적으로 $\alpha^\prime = 1-t$, $\sigma^\prime = t$)

Flow Matching의 PF-ODE는 다음과 같다.

\[\begin{equation} \frac{\textrm{d} \textbf{x}_t}{\textrm{d} t} = \textbf{F}_\theta (\textbf{x}_t, t) \quad \textrm{from} \; t = 0 \; \textrm{to} \; t = 1 \end{equation}\]

Consistency Model

Consistency model (CM)은 신경망 \(\textbf{f}_\theta (\textbf{x}_t, t)\)가 noisy한 입력 \(\textbf{x}_t\)가 PF-ODE의 샘플링 궤적을 따라 1-step으로 데이터 \(\textbf{x}_0\)로 매핑되도록 학습된다. 유효한 \(\textbf{f}_\theta\)는 경계 조건 \(\textbf{f}_\theta (\textbf{x}, 0) = \textbf{x}\)를 만족해야 하며, 이를 만족하는 한 가지 방법은 consistency model을 다음과 같이 parameterize하는 것이다.

\[\begin{equation} \textbf{f}_\theta (\textbf{x}_t, t) = c_\textrm{skip} (t) \textbf{x}_t + c_\textrm{out} (t) \textbf{F}_\theta (c_\textrm{in}(t) \textbf{x}_t, c_\textrm{noise}(t)) \\ \textrm{with} \quad c_\textrm{skip}(0) = 1, \; c_\textrm{out}(0) = 0 \end{equation}\]

CM은 인접한 timestep 사이의 출력이 일관되도록 학습된다. 인접한 timestep이 어떻게 선택되냐에 따라 discrete-time CM과 continuous-time CM으로 구분된다.

Discrete-time CM

Discrete-time CM의 objective는 다음과 같다.

\[\begin{equation} \mathbb{E}_{\textbf{x}_t, t} [w(t) d(\textbf{f}_\theta (\textbf{x}_t, t), \textbf{f}_{\theta^{-}} (\textbf{x}_{t - \Delta t}, t - \Delta t))] \\ \textrm{where} \quad \theta^{-} = \textrm{stopgrad} (\theta) \end{equation}\]

($d(\cdot, \cdot)$는 \(\ell_2\) loss와 같은 metric function)

Continuous-time CM

Discrete-time CM의 objective에서 $d(\textbf{x}, \textbf{y}) = | \textbf{x} - \textbf{y} |_2^2$라 두고 $\Delta t$를 0으로 보내면 gradient가 다음과 같이 된다.

\[\begin{equation} \nabla_\theta \mathbb{E}_{\textbf{x}_t, t} [w(t) \textbf{f}_\theta^\top (\textbf{x}_t, t) \frac{\textrm{d} \textbf{f}_{\theta^{-}} (\textbf{x}_t, t)}{\textrm{d} t}] \\ \textrm{where} \quad \frac{\textrm{d} \textbf{f}_{\theta^{-}} (\textbf{x}_t, t)}{\textrm{d} t} = \nabla_{\textbf{x}_t} \textbf{f}_{\theta^{-}} (\textbf{x}_t, t) + \partial_t \textbf{f}_{\theta^{-}} (\textbf{x}_t, t) \end{equation}\]

\(\frac{\textrm{d} \textbf{f}_{\theta^{-}} (\textbf{x}_t, t)}{\textrm{d} t}\)는 PF-ODE \(\frac{\textrm{d} \textbf{x}_t}{\textrm{d} t}\) 위의 \((\textbf{x}_t, t)\)에서 \(\textbf{f}_{\theta^{-}}\)의 tangent function이다.

Continuous-time CM이나 $\Delta t$가 매우 작은 discrete-time CM을 학습시키는 경우 최적화가 심각하게 불안정하다.

Consistency Distillation & Consistency Training

CM은 consistency distillation (CD) 또는 consistency training (CT)을 사용하여 학습시킬 수 있다. CD에서 CM은 사전 학습된 diffusion model에서 knowledge distillation을 통해 학습된다. 이 diffusion model은 continuous-time CM을 학습시키기 위한 PF-ODE를 제공한다. 더 나아가, PF-ODE를 수치적으로 풀어 \(\textbf{x}_t\)에서 \(\textbf{x}_{t - \Delta t}\)를 구함으로써 discrete-time CM을 학습시킬 수도 있다.

이와 대조적으로 CT는 사전 학습된 diffusion model 없이 처음부터 CM을 학습시킨다. 구체적으로, discrete-time CM에서는 \(\textbf{x}_{t - \Delta t} = \alpha_{t - \Delta t} \textbf{x}_0 + \sigma_{t - \Delta t} \textbf{z}\)로 근사하며, \(\textbf{x}_t\)를 샘플링할 때 동일한 데이터 \(\textbf{x}_0\)와 noise $\textbf{z}$를 재사용한다. Continuous-time CM에서는 PF-ODE \(\frac{\textrm{d}\textbf{x}_t}{\textrm{d}t} \rightarrow \alpha_t^\prime \textbf{x}_0 + \sigma_t^\prime \textbf{z}\)의 추정값을 생성하여, gradient의 추정값을 도출한다.

Simplifying Continuous-Time Consistency Models

기존의 CM은 EDM의 모델 parameterization과 diffusion process 공식을 채택했다. EDM diffusion process는 variance-exploding이므로 (즉, \(\textbf{x}_t = \textbf{x}_0 + t \textbf{z}\)), $c_\textrm{skip} (t) = \frac{\sigma_d^2}{t^2 + \sigma_d^2}$, $c_\textrm{out} (t) = \frac{t \cdot \sigma_d}{\sqrt{t^2 + \sigma_d^2}}$, $c_\textrm{in} (t) = \frac{1}{\sqrt{t^2 + \sigma_d^2}}$를 도출할 수 있다. 이러한 계수는 학습 효율성에 중요하지만 $t$와 \(\sigma_d\)와의 복잡한 산술 관계로 인해 CM의 이론적 분석이 복잡해진다.

EDM과 그에 따른 CM을 단순화하기 위해, 저자들은 EDM의 특성을 유지하면서 \(c_\textrm{skip} (t) = \cos (t)\), \(c_\textrm{out} = - \sigma_d \sin (t)\), \(c_\textrm{in}(t) = 1/\sigma_d\)를 만족하는 diffusion model인 TrigFlow를 제안하였다. TrigFlow는 flow matching의 특수한 경우이고 동시에 EDM 원리를 충족하므로 두 가지 공식의 장점을 결합하는 동시에 diffusion process, 모델 parameterization, PF-ODE, diffusion objective, CM parameterization이 모두 간단한 표현식을 갖도록 한다.

Diffusion Process

\(\textbf{x}_0 \sim p_d (\textbf{x}_0)\)이고 \(\textbf{z} \sim \mathcal{N}(\textbf{0}, \sigma_d^ \textbf{I})\)일 때, noisy한 샘플은 다음과 같이 정의된다.

\[\begin{equation} \textbf{x}_t = \cos (t) \textbf{x}_0 + \sin (t) \textbf{z} \quad \textrm{for} \; t \in [0, \frac{\pi}{2}] \end{equation}\]

Diffusion Models & PF-ODE

Diffusion model은

\[\begin{equation} \textbf{F}_\theta \left( \frac{\textbf{x}_t}{\sigma_d}, c_\textrm{noise} (t) \right) \end{equation}\]

로 parameterize된다. 이에 대응되는 PF-ODE는 다음과 같다.

\[\begin{equation} \frac{\textrm{d}\textbf{x}_t}{\textrm{d}t} = \sigma_d \textbf{F}_\theta \left( \frac{\textbf{x}_t}{\sigma_d}, c_\textrm{noise}(t) \right) \end{equation}\]

Diffusion Objective

TrigFlow에서 diffusion model은 다음 식을 최소화하여 학습된다.

\[\begin{equation} \mathcal{L}_\textrm{Diff} (\theta) = \mathbb{E}_{\textbf{x}_0, \textbf{z}, t} \left[ \left\| \sigma_d \textbf{F}_\theta \left( \frac{\textbf{x}_t}{\sigma_d}, c_\textrm{noise} (t) \right) - \textbf{v}_t \right\|_2^2 \right] \\ \textrm{where} \quad \textbf{v}_t = \cos (t) \textbf{z} - \sin (t) \textbf{x}_0 \end{equation}\]

Consistency Models

경계 조건 \(\textbf{f}_\theta (\textbf{x}, 0) = \textbf{x}\)를 강제하기 위해, first order ODE solver를 사용하여 PF-ODE의 1-step solution으로 CM을 parameterize한다.

\[\begin{equation} \textbf{f}_\theta (\textbf{x}_t, t) = \cos (t) \textbf{x}_t - \sin (t) \sigma_d \textbf{F}_\theta \left( \frac{\textbf{x}_t}{\sigma_d}, c_\textrm{noise} (t) \right) \end{equation}\]

Stabilizing Continuous-Time Consistency Models

저자들은 continuous-time CM 학습의 불안정성 문제를 해결하기 위해, TrigFlow 프레임워크를 기반으로 parameterization, 네트워크 아키텍처, 학습 objective에 초점을 맞춰 continuous-time CM을 안정화하기 위한 몇 가지 이론적 개선 사항을 도입했다.

1. Parameterization and Network Architecture

Continuous-time CM 학습의 핵심은 tangent function \(\frac{\textrm{d} \textbf{f}_{\theta^{-}} (\textbf{x}_t, t)}{\textrm{d} t}\)에 따라 달라지는 gradient이다. TrigFlow에서 tangent function은 다음과 같다.

\[\begin{equation} \frac{\textrm{d} \textbf{f}_{\theta^{-}} (\textbf{x}_t, t)}{\textrm{d} t} = - \cos (t) \left( \sigma_d \textbf{F}_{\theta^{-}} \left( \frac{\textbf{x}_t}{\sigma_d}, t \right) - \frac{\textrm{d} \textbf{x}_t}{\textrm{d} t} \right) - \sin (t) \left( \textbf{x}_t + \sigma_d \frac{\textrm{d} \textbf{F}_{\theta^{-}} \left(\frac{\textbf{x}_t}{\sigma_d}, t \right)}{\textrm{d} t} \right) \end{equation}\]

여기서 \(\frac{\textrm{d}\textbf{x}_t}{\textrm{d}t}\)는 PF-ODE이며, consistency distillation에서 사전 학습된 diffusion model을 사용하여 추정하거나 consistency training에서 noise와 깨끗한 샘플에서 계산된 추정치를 사용한다.

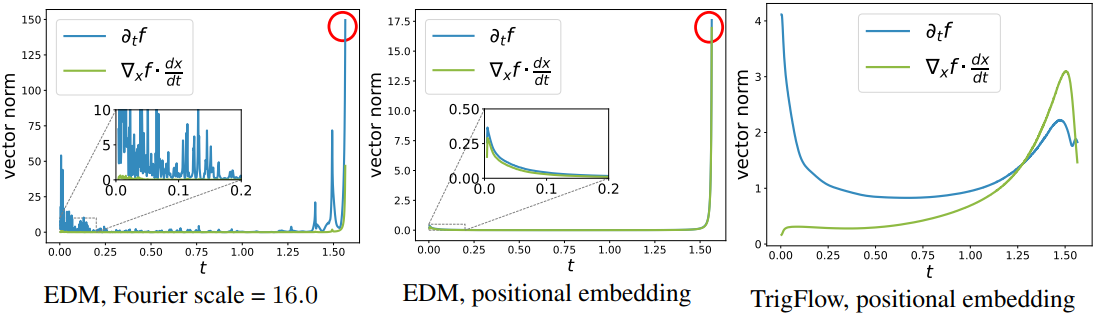
학습을 안정화하기 위해서는 모든 timestep $t$에서 tangent function이 안정해야 한다. 저자들은 경험적으로 \(\sigma_d \textbf{F}_{\theta^{-}}\), \(\frac{\textrm{d}\textbf{x}_t}{\textrm{d}t}\), \(\textbf{x}_t\)가 상대적으로 안정함을 확인했으며, tangent function에서 남은 항은

\[\begin{equation} \sin (t) \frac{\textrm{d} \textbf{F}_{\theta^{-}}}{\textrm{d} t} = \sin (t) \nabla \textbf{x}_t \textbf{F}_{\theta^{-}} \frac{\textrm{d} \textbf{x}_t}{\textrm{d} t} + \sin (t) \partial_t \textbf{F}_{\theta^{-}} \end{equation}\]

이다. 또한 \(\nabla \textbf{x}_t \textbf{F}_{\theta^{-}} \frac{\textrm{d} \textbf{x}_t}{\textrm{d} t}\)는 일반적으로 안정적이므로 (well-conditioned), 불안정성 문제는 \(\sin (t) \partial_t \textbf{F}_{\theta^{-}}\)에서 발생한다. \(\sin (t) \partial_t \textbf{F}_{\theta^{-}}\)는 다음과 같이 분해된다.

\[\begin{equation} \sin (t) \partial_t \textbf{F}_{\theta^{-}} = \sin (t) \frac{\partial c_\textrm{noise}(t)}{\partial t} \cdot \frac{\partial \textrm{emb} (c_\textrm{noise})}{\partial c_\textrm{noise}} \cdot \frac{\partial \textbf{F}_{\theta^{-}}}{\partial \textrm{emb} (c_\textrm{noise})} \end{equation}\]

($\textrm{emb}(\cdot)$는 시간 임베딩이며, positional embedding이나 Fourier embedding)

Identity Time Transformation (\(c_\textrm{noise} (t) = t\))

EDM 공식을 사용하는 대부분의 기존 CM을 TrigFlow 공식으로 변환하면 \(c_\textrm{noise}(t) \propto \log (\sigma_d \tan t)\)가 된다. 그러면 $t$가 $\frac{\pi}{2}$에 가까워지면 \(\sin (t) \cdot \partial_t c_\textrm{noise} (t) = 1 / \cos (t)\)가 무한대로 발산한다. 수치적 안정성을 완화하기 위해, 저자들은 \(c_\textrm{noise} (t) = t\)를 사용하였다.

Positional Time Embeddings

일반적인 시간 임베딩은 \(\textrm{emb}(c) = \sin (s \cdot 2 \pi \omega \cdot c + \phi)\)이며,

\[\begin{equation} \partial_c \textrm{emb}(c) = s \cdot 2 \pi \omega \cdot \cos (s \cdot 2 \pi \omega \cdot c + \phi) \end{equation}\]

가 된다. Fourier scale $s$가 커지면 \(\partial_c \textrm{emb}(c)\)의 크기가 커지고 더 빠르게 진동하기 때문에 불안정성이 발생한다. 이를 피하기 위해, 저자들은 positional embedding을 사용하였으며, 이는 Fourier embedding의 $s \approx 0.02$에 해당한다.

Adaptive Double Normalization

AdaGN layer \(\textbf{y} = \textrm{norm}(\textbf{x}) \odot \textbf{s}(t) + \textbf{b}(t)\)는 CM 학습이 발산하게 만든다. 본 논문에서는 다음과 같은 adaptive double normalization을 사용한다.

\[\begin{equation} \textbf{y} = \textrm{norm}(\textbf{x}) \odot \textrm{pnorm} (\textbf{s} (t)) + \textrm{pnorm} (\textbf{b}(t)) \end{equation}\]

($\textrm{pnorm}(\cdot)$은 pixel normalization)

이 정규화는 diffusion 학습에서 AdaGN의 표현력을 유지하면서도 CM 학습에서 불안정성을 제거한다.

아래 그래프는 CIFAR-10에서 TrigFlow의 안정성을 EDM과 비교한 것이다.

2. Training Objectives

TrigFlow 공식을 사용한 continuous-time CM 학습의 gradient는 다음과 같다.

\[\begin{equation} \nabla_\theta \mathbb{E}_{\textbf{x}_t, t} \left[ -w(t) \sigma_d \sin (t) \textbf{F}_\theta^\top \left( \frac{\textbf{x}_t}{\sigma_d}, t \right) \frac{\textrm{d} \textbf{f}_{\theta^{-}} (\textbf{x}_t, t)}{\textrm{d} t} \right] \end{equation}\]

저자들은 이 gradient를 명시적으로 제어하여 안정성을 개선하기 위해 추가 기법을 제안하였다.

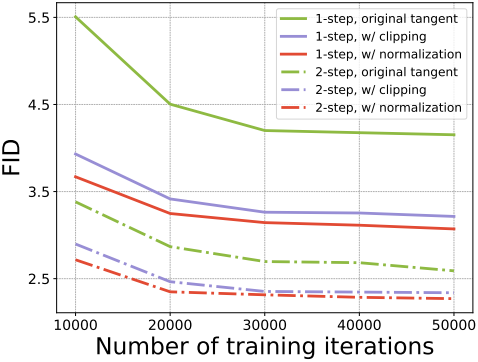
Tangent Normalization

CM 학습의 gradient 분산은 tangent function에서 온다. 저자들은 명시적으로 tangent function을 정규화하였다.

\[\begin{equation} \frac{\textrm{d} \textbf{f}_{\theta^{-}}}{\textrm{d}t} \leftarrow \frac{\frac{\textrm{d} \textbf{f}_{\theta^{-}}}{\textrm{d}t}}{\| \frac{\textrm{d} \textbf{f}_{\theta^{-}}}{\textrm{d}t} \| + 0.1} \end{equation}\]

또다른 방법은 tangent function이 $[-1, 1]$에 있도록 clipping하는 것이다. 두 방법에 대한 효과는 아래 그래프와 같다.

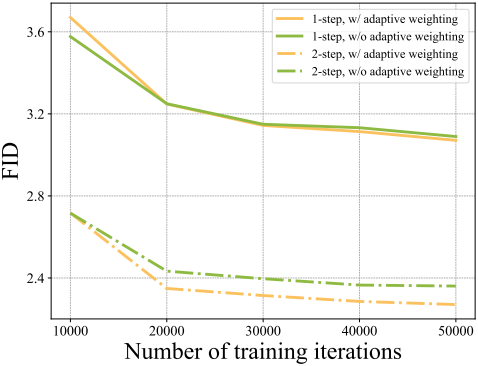
Adaptive Weighting

저자들은 EDM2를 따라, CM과 함께 adaptive weighting function을 학습시키는 것을 제안하였다. 이는 hyperparameter 튜닝의 부담을 덜어줄 뿐만 아니라 더 나은 성능과 무시할 수 있는 학습 오버헤드로 수동으로 설계된 weighting function을 능가한다.

저자들은 $\theta$에 독립적인 임의의 벡터 $\textbf{y}$에 대해, \(\nabla_\theta \mathbb{E}[\textbf{F}_\theta^\top \textbf{y}] = \frac{1}{2} \nabla_\theta \mathbb{E} [\| \textbf{F}_\theta - \textbf{F}_{\theta^{-}} + \textbf{y}\|_2^2]\)임을 이용하였다. Continuous-time CM을 학습시킬 때,

\[\begin{equation} \textbf{y} = -w(t) \sigma_d \sin (t) \frac{\textrm{d} \textbf{f}_{\theta^{-}}}{\textrm{d}t} \end{equation}\]

이다. 이를 이용하면 원래 gradient 식을 MSE objective의 gradient로 변환할 수 있다. 따라서, EDM2와 마찬가지로 timestep에 걸쳐 MSE loss의 분산을 최소화하는 adaptive weighting function을 학습시킬 수 있다. 실제로, prior weighting \(w(t) = \frac{1}{\sigma_d \tan (t)}\)를 통합하면 학습 분산이 더욱 감소한다.

Prior weighting을 통합함으로써, 네트워크 \(\textbf{F}_\theta\)와 adaptive weighting function \(w_\phi (t)\)를 모두 다음을 최소화하여 학습시킨다.

\[\begin{equation} \mathcal{L}_\textrm{sCM}(\theta, \phi) := \mathbb{E}_{\textbf{x}_t, t} \left[ \frac{e^{w_\phi (t)}}{D} \left\| \textbf{F}_\theta \left( \frac{\textbf{x}_t}{\sigma_d}, t \right) - \textbf{F}_{\theta^{-}} \left( \frac{\textbf{x}_t}{\sigma_d}, t \right) - \cos (t) \frac{\textrm{d} \textbf{f}_{\theta^{-}} (\textbf{x}_t, t)}{\textrm{d} t}\right\|_2^2 - w_\phi (t) \right] \end{equation}\]

($D$는 \(\textbf{x}_0\)의 차원, $\tan (t)$는 \(e^{\sigma_d \tan (t)} \sim \mathcal{N}(P_\textrm{mean}, P_\textrm{std}^2)\)이 되도록 log-Normal proposal distribution에서 샘플링)

Adaptive weighting에 대한 효과는 아래 그래프와 같다.

Diffusion Finetuning and Tangent Warmup

기존 CM과 마찬가지로 consistency distillation (CD)의 경우, 사전 학습된 diffusion model에서 CM을 fine-tuning하면 수렴 속도가 빨라질 수 있다.

\(\frac{\textrm{d} \textbf{f}_{\theta^{-}}}{\textrm{d}t}\) 식의 두 번째 항 \(\sin (t) (\textbf{x}_t + \sigma_d \frac{\textrm{d} \textbf{F}_{\theta^{-}}}{\textrm{d}t})\)에서 불안정성이 발생할 수 있으므로, 계수 $\sin (t)$를 $r \cdot \sin (t)$로 대체하는 선택적 테크닉 tangent warmup을 사용할 수 있다. $r$은 처음 10k iteration 동안 0에서 1로 선형적으로 증가한다.

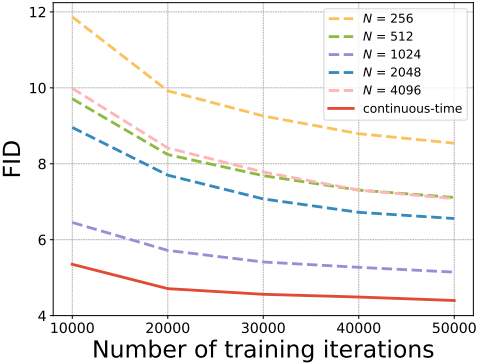
아래는 모든 테크닉을 통합하여 학습시킨 continuous-time CM의 성능을 discrete-time CM과 비교한 그래프이다.

Experiments

• sCD: Consistency distillation으로 학습시킨 scM
• sCT: Consistency trainingdm로 학습시킨 scM

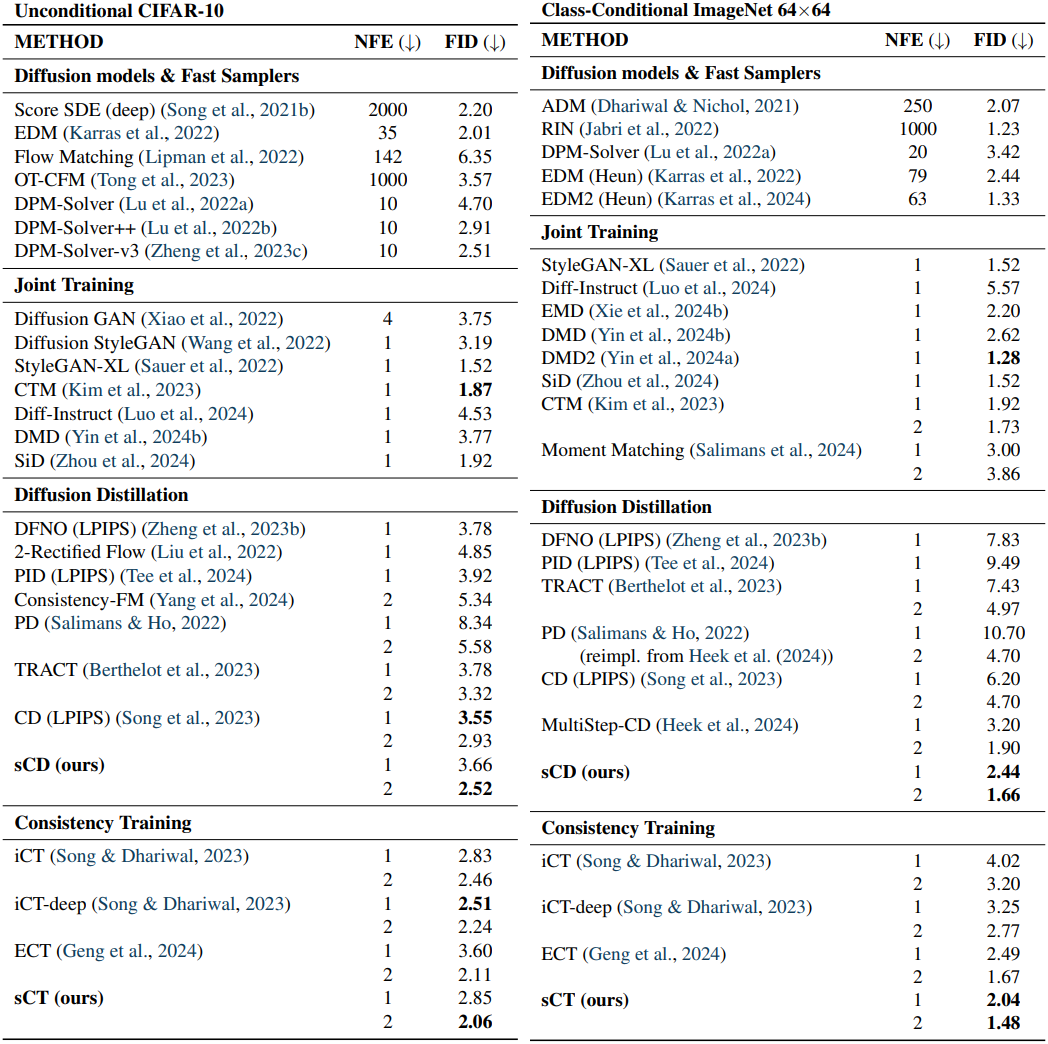
다음은 CIFAR-10과 ImageNet 64$\times$64에서의 성능을 비교한 표이다.

다음은 ImageNet 512$\times$512에서의 성능을 비교한 표이다.

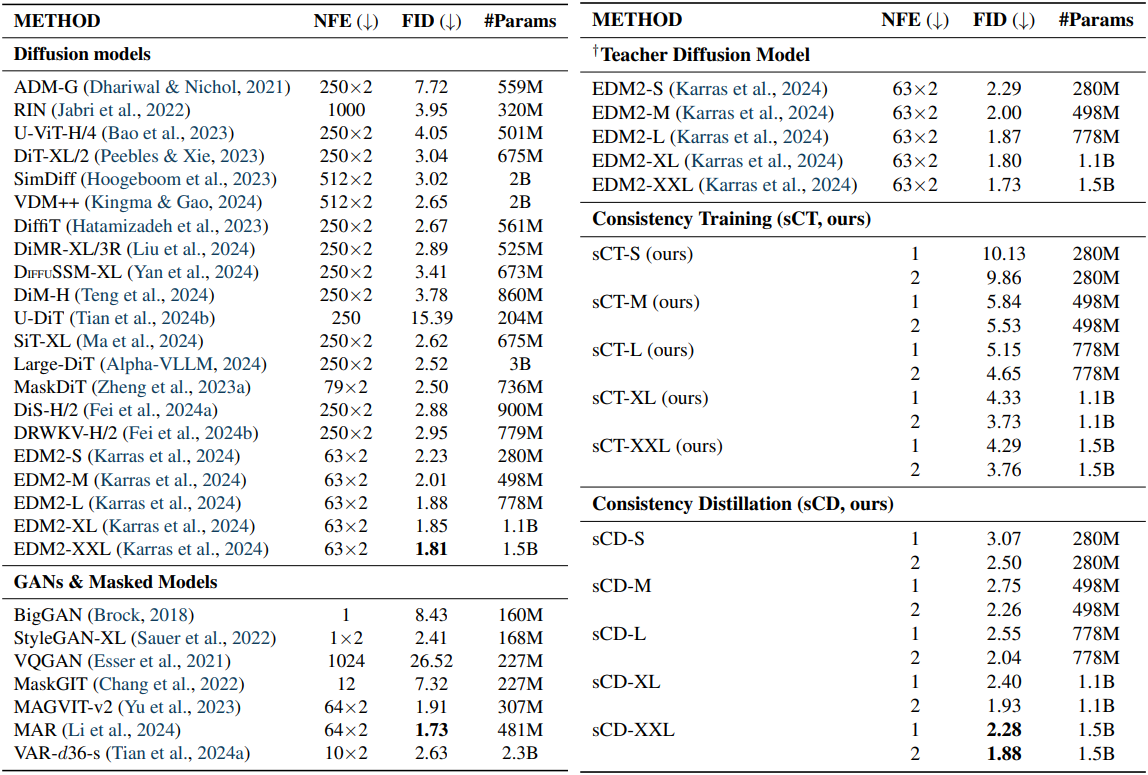
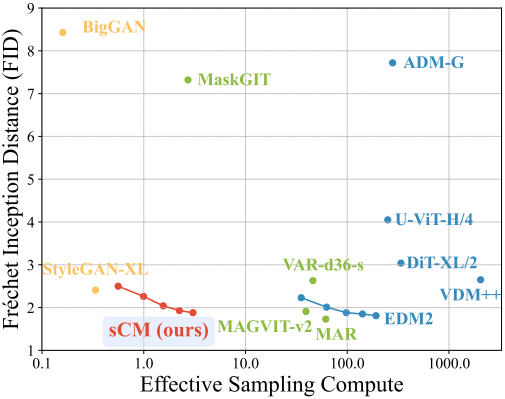
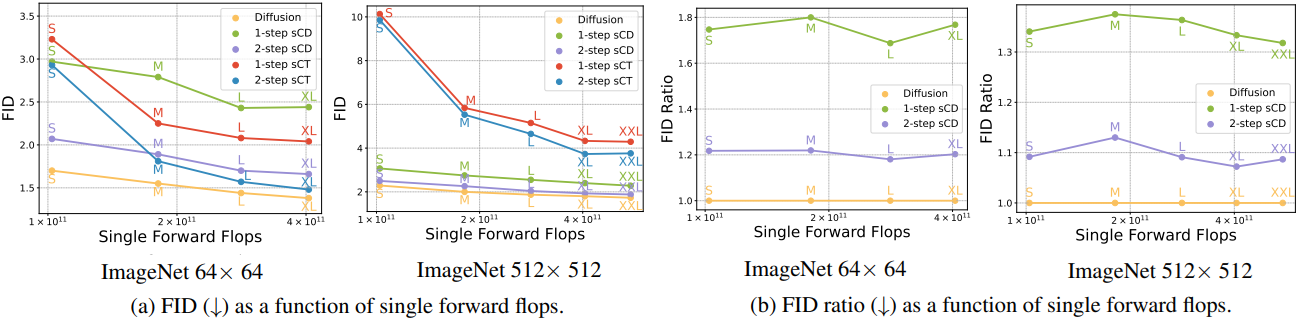
다음은 teacher model의 크기에 맞게 sCD를 scaling한 결과이다.

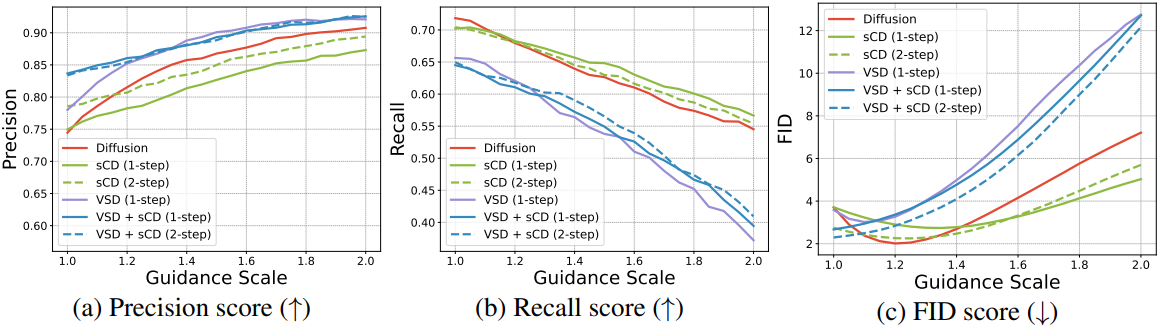
다음은 VSD와 샘플 다양성을 비교한 결과이다.