[논문리뷰] Scaffold-GS: Structured 3D Gaussians for View-Adaptive Rendering

CVPR 2024. [Paper] [Page] [Github]
Tao Lu, Mulin Yu, Linning Xu, Yuanbo Xiangli, Limin Wang, Dahua Lin, Bo Dai
Shanghai Artificial Intelligence Laboratory | The Chinese University of Hong Kong | Nanjing University | Cornell University
30 Nov 2023

Introduction

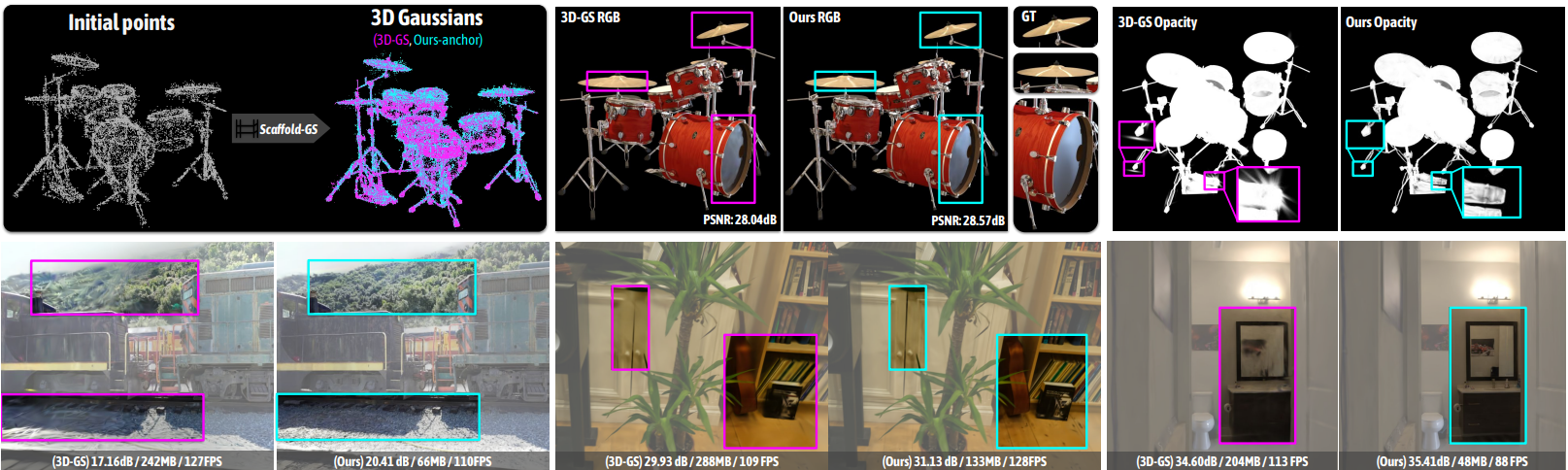
최근에 3D Gaussian Splatting(3D-GS)이 SOTA 렌더링 품질과 속도를 달성했다. Structure from Motion (SfM)에서 파생된 포인트 클라우드에서 초기화된 이 방법은 장면을 표현하기 위해 3D Gaussian 집합을 최적화한다. 3D-GS는 볼류메트릭 표현에서 발견되는 고유한 연속성을 유지하는 동시에 3D Gaussian을 2D 이미지 평면에 스플래팅하여 신속한 rasterization을 촉진하였다.

3D-GS는 여러 가지 장점을 제공하지만 모든 학습 뷰를 수용하기 위해 Gaussian을 과도하게 확장하여 장면 구조를 무시하는 경향이 있다. 이는 특히 복잡한 large-scale scene에서 상당한 중복성을 초래하고 확장성을 제한한다. 또한 뷰에 의존하는 효과들은 interpolation 능력이 거의 없는 개별 Gaussian 파라미터에 적용되므로 상당한 뷰 변경과 조명 효과에 대한 견고성(robustness)이 떨어진다.

본 논문은 앵커 포인트를 활용하여 계층적이고 영역을 인식하는 3D 장면 표현을 설정하는 Gaussian 기반 접근 방식인 Scaffold-GS를 제시하였다. SfM 포인트에서 시작된 앵커 포인트의 sparse한 그리드를 구성한다. 이러한 각 앵커는 학습 가능한 오프셋을 사용하여 일련의 Gaussian들을 연결하며, 이 오프셋의 속성(ex. 불투명도, 색상, 회전, 크기)은 앵커 feature와 보는 위치를 기반으로 동적으로 예측된다. 3D Gaussian이 자유롭게 이동하고 분할할 수 있는 일반 3D-GS와 달리 Scaffold-GS의 전략은 장면 구조를 활용하여 3D Gaussian의 분포를 가이드하고 제한하는 동시에 다양한 뷰 방향과 거리에 로컬하게 적응할 수 있도록 한다. 또한 장면 커버리지를 향상시키기 위해 앵커를 위한 성장 및 pruning 연산을 추가로 개발하였다.

Scaffold-GS는 3D-GS와 동등하거나 심지어 이를 능가하는 렌더링 품질을 제공한다. Inference 시 Gaussian 예측을 view frustum 내의 앵커로 제한하고 불투명도를 기반으로 사소한 Gaussian들을 필터링한다. 결과적으로 계산 오버헤드가 거의 없이 3D-GS와 비슷한 속도로 렌더링할 수 있다. 또한 각 장면에 대해 앵커 포인트와 MLP predictor들만 저장하면 되므로 스토리지 요구 사항이 크게 줄어든다.

Methods

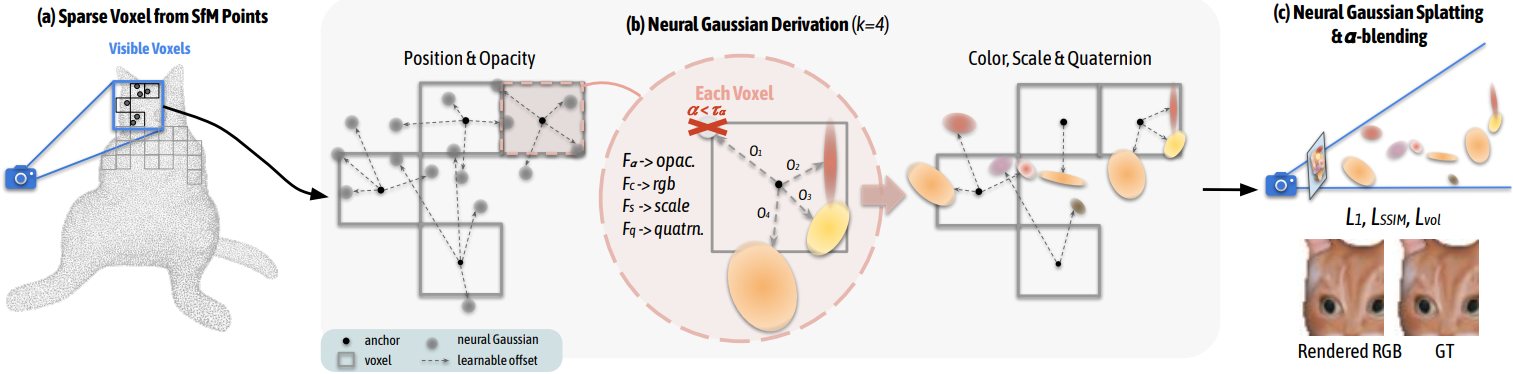
1. Scaffold-GS

Anchor Point Initialization

3D-GS와 마찬가지로 COLMAP의 sparse한 포인트 클라우드를 초기 입력으로 사용한다. 그런 다음 이 포인트 클라우드 $\mathbf{P} \in \mathbb{R}^{M \times 3}$에서 장면을 다음과 같이 voxelize한다.

\[\begin{equation} \mathbf{V} = \bigg\{ \bigg\lfloor \frac{\mathbf{P}}{\epsilon} \bigg\rceil \bigg\} \cdot \epsilon \end{equation}\]

여기서 $\mathbf{V} \in \mathbb{R}^{N \times 3}$은 복셀 중심이고 $\epsilon$은 복셀 크기이다. 그런 다음 $\mathbf{P}$의 중복성과 불규칙성을 줄이기 위해 중복 항목을 제거하며, 이는 \(\{\cdot\}\)로 표시되었다.

각 복셀 $v \in \mathbf{V}$의 중심은 로컬 컨텍스트 feature $f_v \in \mathbb{R}^{32}$, scaling factor $l_v \in \mathbb{R}^3$, $k$개의 학습 가능한 오프셋 \(\mathbf{O}_v \in \mathbb{R}^{k \times 3}\)을 갖춘 앵커 포인트로 처리된다. 저자들은 $f_v$가 다중 해상도와 뷰 의존성을 갖도록 다음과 같이 추가로 향상시켰다.

1. Feature bank \(\{f_v, f_{v_{\downarrow_1}}, f_{v_{\downarrow_2}}\)를 생성한다. 여기서 \(\downarrow_n\)은 $f_v$가 $2^n$배 다운샘플링됨을 나타낸다.
2. 통합된 앵커 feature \(\hat{f_v}\)를 형성하기 위해 feature bank를 뷰에 의존하는 가중치와 혼합한다. 구체적으로, 카메라가 \(\mathbf{x}_c\)에 있고 앵커가 \(\mathbf{x}_v\)에 있으면 다음과 같이 상대적 거리와 시야 방향을 계산한다.

\[\begin{equation} \delta_{vc} = \| \mathbf{x}_v - \mathbf{x}_c \|_2, \quad \vec{\mathbf{d}}_{vc} = \frac{\mathbf{x}_v - \mathbf{x}_c}{\| \mathbf{x}_v - \mathbf{x}_c \|_2} \end{equation}\]

그런 다음 작은 MLP $F_w$에서 예측된 가중치를 사용하여 feature bank를 가중 합산한다.

\[\begin{equation} \{w, w_1, w_2\} = \textrm{Softmax} (F_w (\delta_{vc}, \vec{\mathbf{d}}_{vc})) \\ \hat{f_v} = w \cdot f_v + w_1 \cdot f_{v_{\downarrow_1}} + w_2 \cdot f_{v_{\downarrow_2}} \end{equation}\]

Neural Gaussian Derivation

위치 $\mu \in \mathbb{R}^3$, 불투명도 $\alpha \in \mathbb{R}$, 공분산에 대한 quarternion $q \in \mathbb{R}^4$, scale $s \in \mathbb{R}^3$, 색상 $c \in \mathbb{R}^3$을 사용하여 Gaussian들을 parameterize한다. 위 그림의 (b)와 같이 viewing frustum 내의 각 앵커 포인트에 대해 $k$개의 Gaussian들을 생성하고 해당 속성을 예측한다. 구체적으로, \(\mathbf{x}_v\)에 위치한 앵커 포인트가 주어지면 Gaussian들의 위치는 다음과 같이 계산된다.

\[\begin{equation} \{\mu_0, \ldots, \mu_{k-1}\} = \mathbf{x}_v + \{ \mathcal{O}_0, \ldots, \mathcal{O}_{k-1} \} \cdot l_v \end{equation}\]

여기서 \(\{ \mathcal{O}_0, \ldots, \mathcal{O}_{k-1} \} \in \mathbb{R}^{k \times 3}\)은 학습 가능한 오프셋이고 $l_v$는 해당 앵커와 관련된 scaling factor이다. $k$개의 Gaussian들의 속성은 개별 MLP $F_\alpha$, $F_c$, $F_q$, $F_s$를 통해 앵커 feature \(\hat{f_v}\), 상대적 거리 \(\delta_{vc}\), 카메라와 앵커 포인트 사이의 방향 \(\vec{\mathbf{d}}_{vc}\)에서 직접 디코딩된다. 속성들은 one-pass로 디코딩된다. 예를 들어 앵커 포인트에서 생성된 Gaussian의 불투명도 값은 다음과 같이 계산된다.

\[\begin{equation} \{\alpha_0, \ldots, \alpha_{k-1}\} = F_\alpha (\hat{f_v}, \delta_{vc}, \vec{\mathbf{d}}_{vc}) \end{equation}\]

색상 \(\{c_i\}\), quaternion \(\{q_i\}\), scale \(\{s_i\}\)도 유사하게 계산된다.

Gaussian 속성들의 예측은 즉석에서 수행된다. 즉, frustum 내에 표시되는 앵커만 활성화되어 Gaussian을 생성한다. Rasterization을 더욱 효율적으로 만들기 위해 불투명도 값이 미리 정의된 threshold $\tau_\alpha$보다 큰 Gaussian들만 유지한다. 이는 계산 부하를 실질적으로 줄이고 3D-GS와 동등한 높은 렌더링 속도를 유지하는 데 도움이 된다.

2. Anchor Points Refinement

Growing Operation

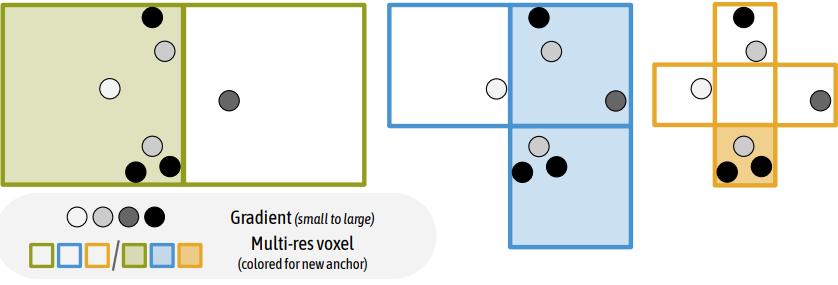
Gaussain들은 SfM 포인트에서 초기화되는 앵커 포인트에 밀접하게 연결되어 있으므로 모델링 능력은 로컬한 영역으로 제한된다. 이로 인해 특히 텍스처가 없고 관찰이 잘 안되는 영역에서 앵커 포인트의 초기 배치가 어려워진다. 따라서 저자들은 Gaussian이 중요하다고 생각하는 새로운 앵커를 성장시키는 오차 기반 앵커 성장 정책을 제안하였다. 중요한 영역을 결정하기 위해 먼저 크기 $\epsilon_g$의 복셀을 구성하여 Gaussian들을 공간적으로 quantize한다. 각 복셀에 대해 $N$번의 학습 iteration에 대해 포함된 Gaussian들 평균 기울기 $\nabla_g$를 계산한다. 그런 다음 $\nabla_g > \tau_g$인 복셀은 중요한 것으로 간주된다. 여기서 $\tau_g$는 미리 정의된 threshold이다. 그러면 앵커 포인트가 설정되지 않은 경우 새 앵커 포인트가 해당 복셀의 중심에 배치된다. 위 그림은 이러한 연산을 보여준다. 실제로 저자들은 공간을 다중 해상도 복셀 그리드로 quantize하여 새로운 앵커가 여러 세분성으로 추가될 수 있도록 하였다.

\[\begin{equation} \epsilon_g^{(m)} = \frac{\epsilon_g}{4^{m-1}}, \quad \tau_g^{(m)} = \tau_g \cdot 2^{m-1} \end{equation}\]

여기서 $m$은 quantization의 수준이다. 새로운 앵커 추가를 더욱 규제하기 위해 이러한 후보에 랜덤 제거를 적용한다. 포인트 추가에 대한 이러한 신중한 접근 방식은 앵커의 급격한 확장을 효과적으로 억제한다.

Pruning Operation

사소한 앵커를 제거하기 위해 $N$번의 학습 iteration동안 연관된 Gaussian의 불투명도 값을 누적한다. 앵커가 만족스러운 수준의 불투명도로 Gaussian을 생성하지 못하면 장면에서 앵커를 제거한다.

3. Losses Design

렌더링된 픽셀 색상에 대한 \(\mathcal{L}_1\) loss와 SSIM 항 \(\mathcal{L}_\textrm{SSIM}\), 볼륨 정규화 \(\mathcal{L}_\textrm{vol}\)을 사용하여 학습 가능한 파라미터와 MLP를 최적화한다. 전체 loss는 다음과 같다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_1 + \lambda_\textrm{SSIM} \mathcal{L}_\textrm{SSIM} + \lambda_\textrm{vol} \mathcal{L}_\textrm{vol} \end{equation}\]

여기서 볼륨 정규화 \(\mathcal{L}_\textrm{vol}\)은 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{vol} = \sum_{i=1}^{N_\textrm{ng}} \textrm{Prod} (s_i) \end{equation}\]

$N_\textrm{ng}$는 장면의 Gaussian 수를 나타내고 $\textrm{Prod}(\cdot)$는 벡터 값의 곱이며, $s_i$는 Gaussian들의 scale이다. 볼륨 정규화 항은 Gaussian이 최소한의 중첩으로 작아지도록 권장한다.

Experiments

• 데이터셋: Mip-NeRF360, Tanks&Temples, DeepBlending, synthetic Blender, BungeeNeRF, VR-NeRF

1. Results Analysis

Comparisons

다음은 현실 세계의 데이터셋에서 이전 방법들과 성능을 비교한 표이다.

다음은 현실 세계의 데이터셋에서 이전 방법들과 렌더링 속도와 저장 용량을 비교한 표이다.

다음은 다양한 데이터셋에서 Scaffold-GS와 3D-GS의 결과를 비교한 것이다.

Multi-scale Scene Contents

다음은 large-scale scene에서 Scaffold-GS와 3D-GS의 성능 및 저장 용량을 비교한 표이다.

다음은 BungeeNeRF의 multi-scale scene에서 Scaffold-GS와 3D-GS의 결과를 비교한 것이다.

Feature Analysis

다음은 앵커 feature를 3개로 클러스터링한 결과이다.

View Adaptability

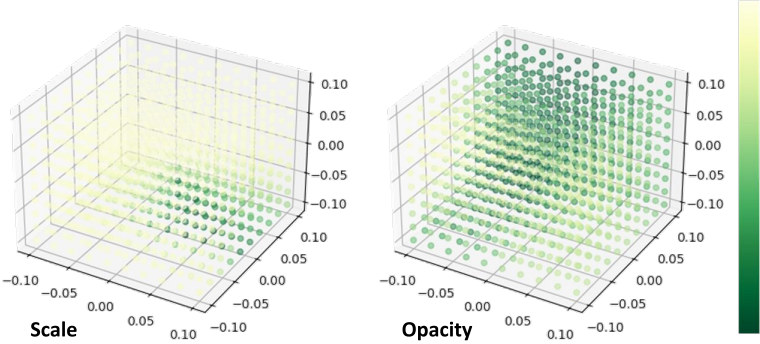
다음은 다양한 위치에서 관찰된 하나의 Gaussian의 디코딩된 속성을 시각화한 것이다. 각 포인트는 공간의 시점에 해당한다. 포인트의 색상은 이 뷰에 대해 디코딩된 속성의 강도를 나타낸다.

Selection Process by Opacity

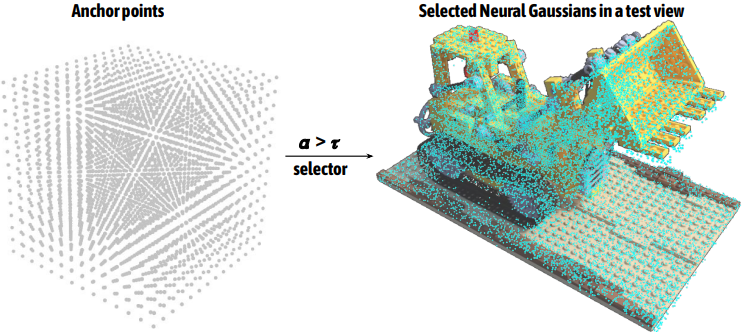
다음은 무작위로 초기화된 포인트의 앵커 포인트(왼쪽)와 현재 뷰에 대해 활성화된 Gaussian들(오른쪽)이다.

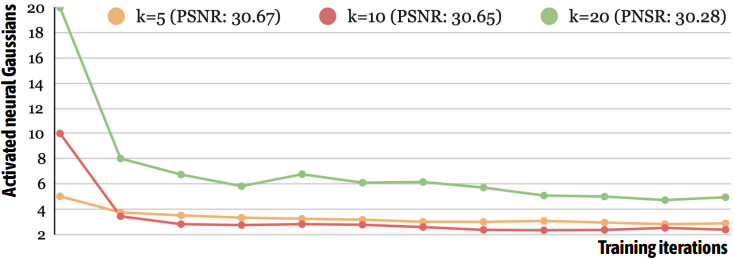
다음은 학습 가능한 오프셋 수 $k$에 따른 활성화된 Gaussian들의 수를 나타낸 그래프이다. $k$가 다르더라도 비슷한 수로 수렴하는 것을 볼 수 있다.

2. Ablation Studies

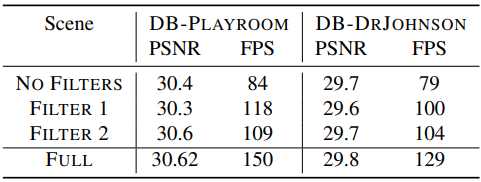
다음은 필터링에 대한 ablation study 결과이다. Filter 1은 view frustum에 의한 필터링이고, Filter 2는 불투명도 기반 필터링이다.

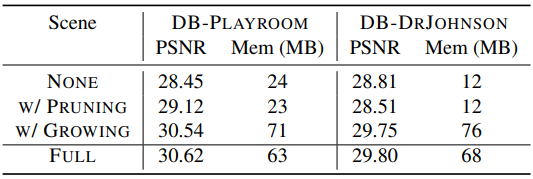
다음은 anchor refinement에 대한 ablation study 결과이다.

Limitations

초기 포인트가 충실도 높은 결과에 중요한 역할을 한다. SfM 포인트 클라우드에서 프레임워크를 초기화하는 것은 신속하고 실행 가능한 솔루션이지만, 텍스처가 없는 대규모 영역이 지배적인 시나리오에서는 최선이 아닐 수 있다. 앵커 포인트 개선 전략으로 이 문제를 어느 정도 해결할 수 있음에도 불구하고 여전히 극도로 sparse한 포인트로 인해 어려움을 겪고 있다.