[논문리뷰] Score-Based Generative Modeling through Stochastic Differential Equations
ICLR 2021. [Paper] [Github]
Yang Song, Jascha Sohl-Dickstein, Diederik P. Kingma, Abhishek Kumar, Stefano Ermon, Ben Poole
Stanford University | Google Brain
26 Nov 2020
Introduction
확률적 생성 모델에는 성공적인 분야가 두 가지 있는데, 하나는 Score matching with Langevin dynamics (SMLD)이고, 다른 하나는 DDPM (논문리뷰)이다. 두 클래스 모두 천천히 증가하는 noise로 학습 데이터를 순차적으로 손상시키고 이를 되돌리는 방법을 생성 모델이 학습한다. SMLD는 score(ex. 로그 확률 밀도의 기울기)를 각 noise scale에서 학습하고 Langevin dynamics로 샘플링한다. DDPM은 학습이 tractable하도록 reverse distribution을 정의하여 각 step을 reverse한다. 연속적인 state space의 경우 DDPM의 목표 함수는 암시적으로 각 noise sclae에서 점수를 계산한다. 따라서 이 두 모델 클래스를 함께 score 기반 생성 모델이라고 한다.
Score 기반 생성 모델은 이미지나 오디오 등의 다양한 생성 task에 효과적인 것으로 입증되었다. 저자들은 확률적 미분 방정식(Stochastic Differential Equations, SDE)을 통해 이전 접근 방식을 일반화하는 통합 프레임워크를 제안한다. 이를 통해 새로운 샘플링 방법이 가능하고 score 기반 생성 모델의 기능이 더욱 확장된다.
특히, 저자들은 유한 개의 noise 분포 대신 diffusion process에 의해 시간이 지남에 따라 진화하는 분포의 연속체(continuum)를 고려하였다. 이 프로세스는 점진적으로 데이터 포인트를 random noise로 확산시키고 데이터에 의존하지 않고 학습 가능한 parameter가 없는 SDE에 의해 가능하다. 이 프로세스를 reverse하여 random noise를 샘플 생성을 위한 데이터로 만들 수 있다. 결정적으로, 이 reverse process는 reverse-time SDE를 충족하며, 이는 시간의 함수로서 주변 확률 밀도의 score가 주어진 forward SDE에서 유도할 수 있다. 따라서 시간에 의존하는 신경망을 학습시켜 score를 추정한 다음 numerical SDE solver로 샘플을 생성하여 reverse-time SDE를 근사할 수 있다.
아래 그림으로 이 아이디어를 요약할 수 있다.

저자들이 제안한 프레임워크는 몇 가지 이론적이고 실용적인 기여가 있다.
Flexible sampling and likelihood computation
먼저, 샘플링을 위해 general-purpose SDE solver를 사용하여 reverse-time SDE를 통합할 수 있다. 또한 일반적인 SDE에는 사용할 수 없는 두 가지 특별한 방법이 가능하다.
- Numerical SDE solver와 score 기반의 MCMC(Markov chain Monte Carlo)를 합친 Predictor-Corrector (PC) sampler
→ Score 기반 모델에 대한 기존 샘플링 방법을 통합하고 개선 - Probability flow ODE에 기반한 deterministic sampler
→ Black-box ODE solver를 통한 빠른 적응형 샘플링, latent code를 통한 유연한 데이터 조작, 고유하게 식별 가능한 인코딩, 정확한 likelihood 계산이 가능
Controllable generation
Unconditional score에서 conditional reverse-time SDE를 효율적으로 추정할 수 있기 때문에 학습 중에 사용할 수 없는 정보를 조건으로 생성 프로세스를 조정할 수 있다. 이를 통해 클래스 조건부 이미지 생성, 인페인팅, colorization 등과 같은 inverse problem을 모두 재학습 없이 단일 unconditional score 기반 모델을 사용하여 풀 수 있다.
Unified framework
저자들의 프레임워크는 score 기반 생성 모델을 개선하기 위해 다양한 SDE를 탐색하고 조정하는 통합된 방법이다. SMLD와 DDPM은 두 개의 개별 SDE의 discretization으로 프레임워크에 통합할 수 있다. 최근에 DDPM이 SMLD보다 더 높은 샘플 품질을 달성하지만 프레임워크의 더 나은 아키텍처와 새로운 샘플링 알고리즘을 통해 SMLD가 따라잡을 수 있다. CIFAR-10에서 IS(9.89)와 FID(2.20)이 state-of-the-art를 달성했으며, score 기반 모델에서 처음으로 1024$\times$1024에서 fidelity 높은 이미지 생성이 가능하다. 또한 균일하게 dequantize된 CIFAR-10 이미지에서 새로운 SDE를 통해 2.99bits/dim의 likelihood 값을 달성하는 새로운 기록을 세웠다.
Background
1. Denoising score matching with Langevin dynamics (SMLD)
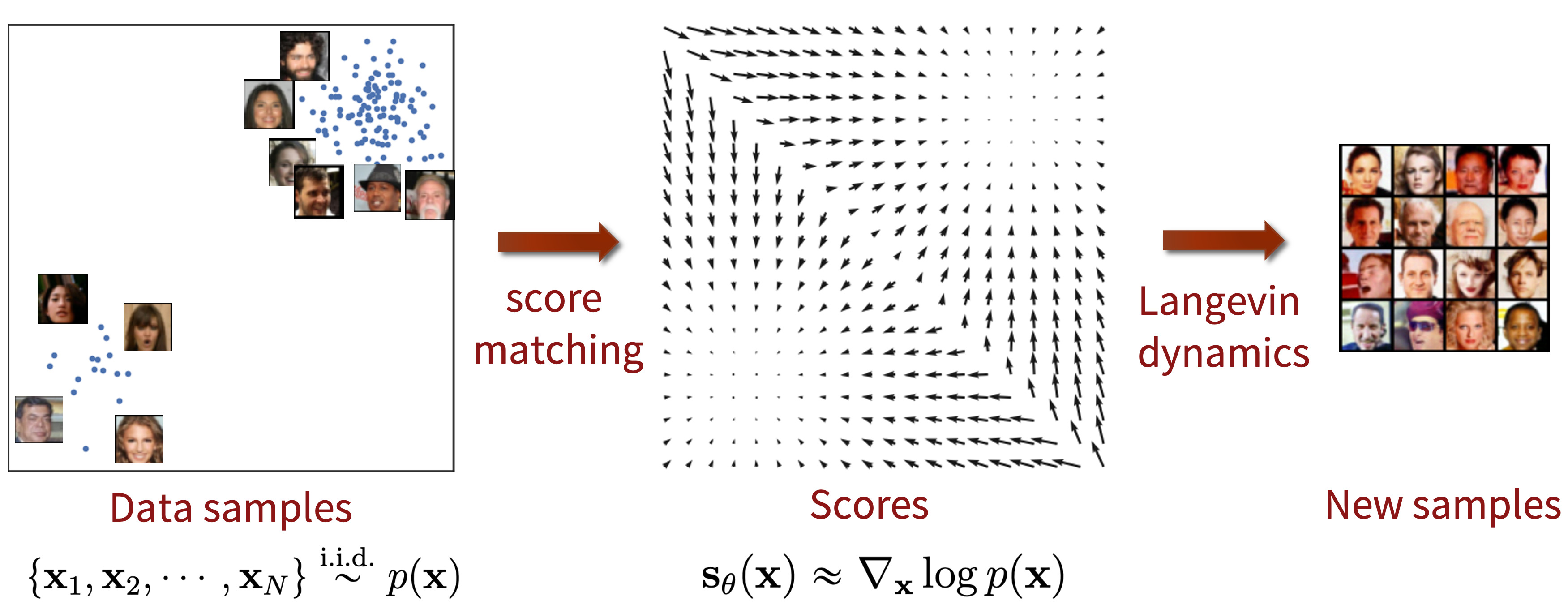
Score 기반의 생성 모델은 random noise에서 시작해서 score (log likelihood의 기울기 $\nabla_x \log p(x)$)를 따라 조금씩 이동하여 (gradient ascent) 최종적으로 데이터와 비슷한 이미지를 생성하는 모델이다. 이를 위해 다음과 같이 score를 ground truth로 하여 score를 추정하기 위한 모델 $s_\theta$를 학습시키며, 이를 score matching이라 부른다.
$s_\theta (x)$가 $\nabla_x \log p(x)$와 가깝게 잘 학습이 되었다면 다음과 같이 Langevin dynamics로 샘플링을 한다.
\[\begin{equation} x_{i+1} = x_i + \epsilon_i s_\theta (x_i) + \sqrt{2 \epsilon_i} z_i, \quad \quad z_i \sim \mathcal{N} (0, I) \end{equation}\]Langevin dynamics에 의해 아래와 같이 random noise에서 시작하여 입력 이미지의 분포에 맞는 데이터 포인트로 이동한다.

위의 방법으로 모델을 학습시키면 한 가지 추가적인 문제점이 발생한다. 데이터가 likelihood가 높은 부분에서 샘플링되기 때문에 likelihood가 낮은 부분의 score를 모델이 추정하기 어렵다는 것이다. 즉, likelihood가 높은 부분의 score만을 ground truth로 제공받기 때문에 모든 부분에서의 score를 계산하지 못하게 된다. 만일 likelihood가 낮은 부분에서 random noise가 뽑혀 샘플링이 진행된다면 score가 부정확하기 때문에 최종적으로 입력 데이터에 해당하는 부분으로 이동하지 못할 것이다.
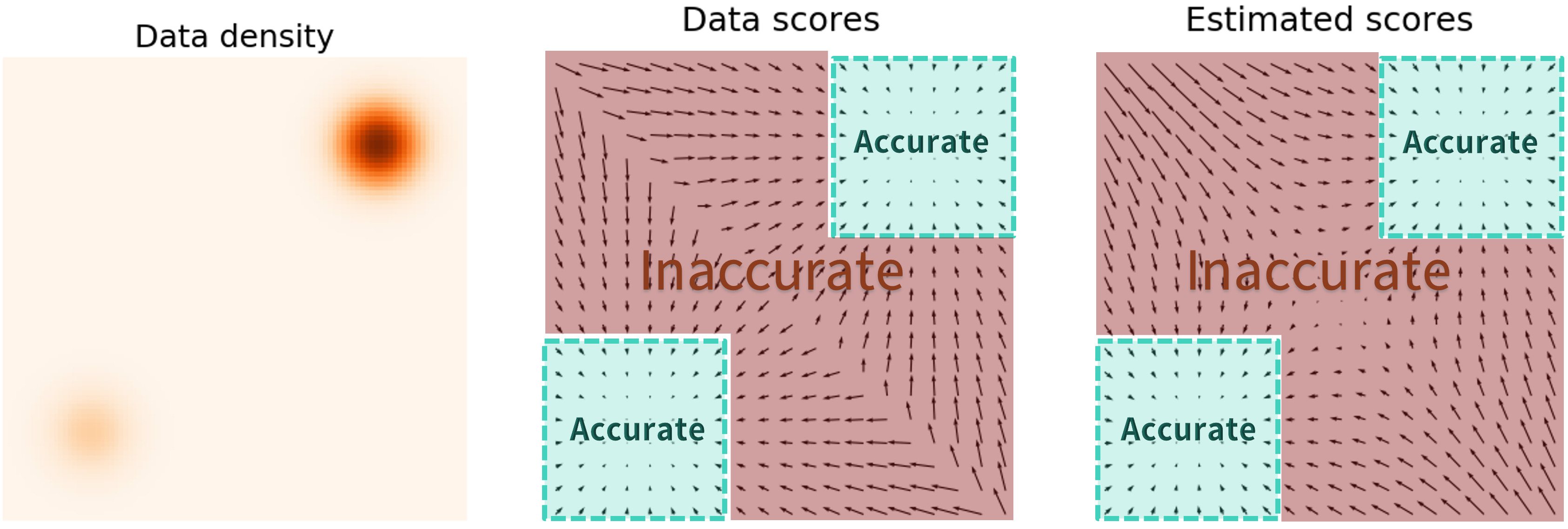
이러한 한계점을 극복한 것이 Denoising score matching (2011)이다.
Denoising score matching은 입력 데이터에 약간의 Gaussian noise를 추가한 pertubed data distribution $p_\sigma (\tilde{x} \vert x) := \mathcal{N}(\tilde{x}; x, \sigma^2 I)$의 score가 noise가 충분히 작은 경우 원래 데이터의 score와 거의 같다는 것을 이용하여 score를 추정하는 방법이다. 즉, likelihood가 낮은 공간을 noise가 채워서 score를 추정할 수 있도록 하는 것이다.

아래와 같은 식을 사용하여 모델을 학습시킨다.
위 식에서 $s_\theta (\tilde{x}, \sigma)$는 Noise Conditional Score Network (NCSN)라 부른다.
NCSN에 대하여 Langevin dynamics를 사용하여 샘플링이 진행됨에 따라 점점 likelihood가 높은 곳으로 이동할 것이기 때문에 계속 큰 $\sigma$를 사용할 필요가 없다. 따라서, 양의 noise scale의 수열 $\sigma_{\textrm{min}} = \sigma_1 < \sigma_2 < \cdots < \sigma_N = \sigma_{\textrm{max}}$를 두고, $\sigma_{\textrm{max}}$부터 시작해서 순차적으로 $\sigma$를 줄여서 마지막에는 $\sigma_{\textrm{min}}$을 사용하도록 한다. SMLD 논문에서는 NCSN $s_\theta (x, \sigma)$을 다음과 같은 denoising score matching objective의 가중치 합으로 학습시킨다.
\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \min} \sum_{i=1}^N \sigma_i^2 \mathbb{E}_{p_{\textrm{data}}(x)} \mathbb{E}_{p_{\sigma_i}(\tilde{x}|x)} [\| s_\theta (\tilde{x}, \sigma_i) - \nabla_{\tilde{x}} \log p_{\sigma_i} (\tilde{x}|x) \|_2^2] \end{equation}\]데이터와 모델의 capacity가 충분하다면 최적의 score 기반 모델 $s_{\theta^\ast}$는 \(\sigma \in \{\sigma_i\}_{i=1}^N\)에 대해 거의 모든 곳에서 $\nabla_x \log p_\sigma (x)$와 일치한다. 샘플링 시에서는 $M$ step의 Langevin MCMC로 다음과 같이 순차적으로 각 $p_{\sigma_i} (x)$를 샘플링한다.
\[\begin{equation} x_i^m = x_i^{m-1} + \epsilon_i s_{\theta^\ast} (x_i^{m-1}, \sigma_i) + \sqrt{2 \epsilon_i} z_i^m, \quad \quad m = 1, 2, \cdots, M \end{equation}\]$\epsilon_i > 0$은 step의 크기이며 $z_i^m$은 표준 정규분포에서 뽑는다.
위 식은 $i = N, N-1, \cdots, 1$에 대하여 반복되며, $i = N$일 때 $x_N^0 \sim \mathcal{N} (x \vert 0, \sigma_{\textrm{max}}^2 I)$이고 $i < N$일 때 $x_i^0 = x_{i+1}^M$이다. $M$이 무한에 가까워지고 $\epsilon_i$가 모든 $i$에 대하여 0에 가까워질 때, 일부 regularity 조건에서 $x_1^M$은 $p_{\sigma_{\textrm{min}}} (x) \approx p_{\textrm{data}} (x)$에 적합한 샘플이 된다.
2. DDPM
(자세한 내용은 논문리뷰 참고)
DDPM 논문은 양의 noise scale의 수열 $0 < \beta_1, \beta_2, \cdots, \beta_N < 1$을 사용한다. 각 학습 데이터 $x_0$에 대하여
\[\begin{equation} p(x_i \vert x_{i-1}) = \mathcal{N} (x_i; \sqrt{1-\beta_i} x_{i-1}, \beta_i I) \end{equation}\]를 만족하는 discrete한 Markov chain \(\{x_0, x_1, \cdots, x_N\}\)을 구성한다. $x_i$는
\[\begin{equation} p_{\alpha_i} (x_i \vert x_0) = \mathcal{N} (x_i; \sqrt{\alpha_i} x_0, (1- \alpha_i)I), \quad \quad \alpha_i := \prod_{j=1}^i (1-\beta_j) \end{equation}\]로 바로 구할 수 있다. 또한 $x_N$은 $\mathcal{N}(0,I)$와 거의 같다.
역방향의 variational Markov chain은
\[\begin{equation} p_\theta (x_{i-1} \vert x_i) = \mathcal{N}(x_{i-1}; \frac{1}{\sqrt{1-\beta_i}} (x_i + \beta_i s_\theta (x_i, i)), \beta_i I) \end{equation}\]로 parameterize된다. $s_\theta (x_i, i)$는 다음과 같은 가중치를 재조정한 ELBO로 학습된다.
\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \min} \sum_{i=1}^N (1-\alpha_i) \mathbb{E}_{p_\textrm{data} (x)} \mathbb{E}_{p_{\alpha_i} (\tilde{x} | x)} [\|s_\theta (\tilde{x}, i) - \nabla_{\tilde{x}} \log p_{\alpha_i} (\tilde{x} | x)\|_2^2] \end{equation}\]최적의 모델 $s_{\theta^\ast} (x, i)$로 $x_N \sim \mathcal{N}(0,I)$로부터 샘플을 생성하며, 이 때 다음의 reverse Markov chain을 사용한다.
\[\begin{equation} x_{i-1} = \frac{1}{\sqrt{1-\beta_i}} (x_i + \beta_i s_{\theta^\ast} (x_i, i)) + \sqrt{\beta_i} z_i, \quad \quad i = N, N-1, \cdots, 1 \end{equation}\]이와 같이 미리 정의한 조건부 확률 분포로부터 이미지를 샘플링하는 방법을 ancestral sampling이라 부른다.
Score-Based Generative Modeling with SDEs
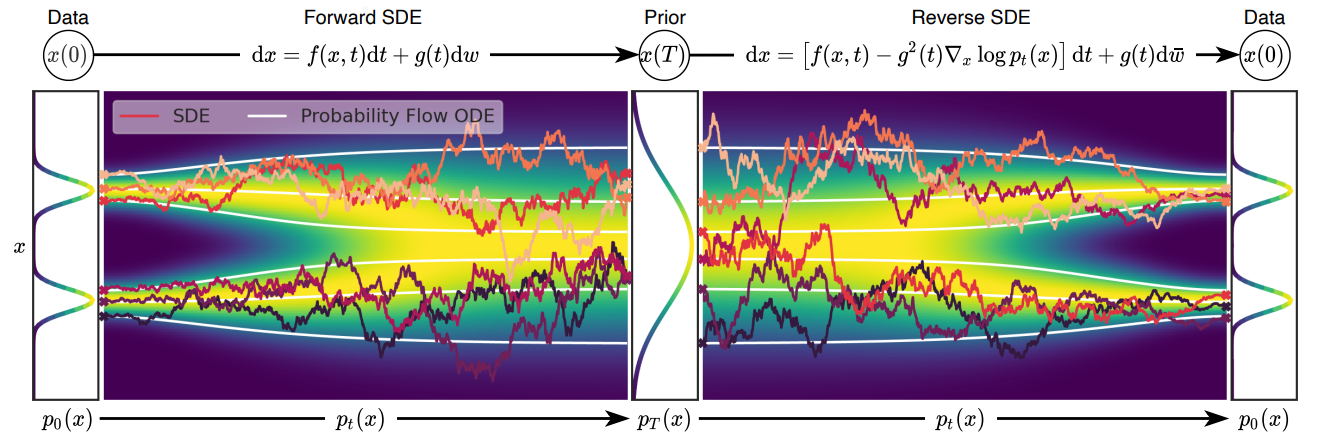
1. Perturbing Data with SDEs
본 논문의 목표 중 하나는 $x(0) \sim p_0$가 데이터 분포이고 $x(T) \sim p_T$가 사전 확률 분포가 되도록 연속적인 시간 변수 $t \in [0, T]$로 표현되는 diffusion process \(\{x(t)\}_{t=0}^T\)를 만드는 것이다. 이 diffusion process는 다음과 같은 Itô SDE의 해로 모델링할 수 있다.
\[\begin{equation} dx = f(x,t)dt + g(t)dw \end{equation}\]여기서 $w$는 브라운 운동과 같은 standard Wiener process이다. $f$는 drift coefficient라 불리는 벡터 함수이고 $g$는 diffusion coefficient라 불리는 스칼라 함수이다.
SDE는 coefficient가 상태와 시간 모두에서 전역적으로 Lipschitz인 경우 고유하고 강력한 해를 갖는다.
(Lipschitz 함수: 두 점 사이의 거리를 일정 비 이상으로 증가시키지 않는 함수)
여기서부터 $x(t)$의 확률 밀도를 $p_t(x)$로 표시하고 $p_{st}(x(t)\vert x(s))$는 $x(s)$에서 $x(t)$로의 transition kernel을 나타낸다. ($0 \le s < t \le T$)
일반적으로 $p_T$는 $p_0$의 정보를 가지고 있지 않은 unstructured prior distribution이다. (ex. 고정된 평균과 분산을 가지는 가우시안 분포.) 다양한 방법으로 데이터 분포가 고정된 사전 확률 분포로 확산하도록 위 식을 이용하여 SDE를 설계할 수 있다.
2. Generating Samples by Reversing the SDE
$x(T) \sim p_T$에서 시작하여 process를 reverse하여 샘플 $x(0) \sim p_0$를 얻을 수 있다. Diffusion process의 reverse도 diffusion process이며 시간의 반대 방향으로 진행되는 reverse-time SDE는 다음과 같다.
\[\begin{equation} dx = [f(x,t) - g(t)^2 \nabla_x \log p_t (x)] dt + g(t) d \bar{w} \end{equation}\]$\bar{w}$는 standard Wiener process이고, 시간이 $T$에서 0으로 뒤로 흐른다. $dt$는 0에 가까운 음의 무한소 timestep이다. 주변 확률 분포의 score $\nabla_x \log p_t (x)$를 모든 $t$에 대해 알고 있다면 위의 식으로부터 reverse diffusion process을 유도할 수 있으며, $p_0$에서 샘플링하도록 시뮬레이션할 수 있다.
3. Estimating Scores for the SDE
분포의 score은 score matching으로 score 기반 모델을 학습시켜 추정할 수 있다. 시간에 의존하는 score 기반 모델 $s_\theta (x, t)$를 다음과 같이 학습시켜 $\nabla_x \log p_t (x)$를 추정할 수 있다.
\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \min} \mathbb{E}_t \bigg\{ \lambda (t) \mathbb{E}_{x(0)} \mathbb{E}_{x(t)} [\| s_\theta (x(t), t) - \nabla_{x(t)} \log p_{0t} (x(t) | x(0) \|_2^2)] \bigg\} \end{equation}\]여기서 \(\lambda : [0:T] \rightarrow \mathbb{R}_{>0}\)는 양의 가중치 함수이며, $t$는 $[0:T]$에서 uniform하게 샘플링한다. 또한 $x(0) \sim p_0 (x)$이고 $x(t) \sim p_{0t} (x(t) \vert x(0))$이다. 데이터와 모델의 capacity가 충분하다면 score matching은 최적해 $s_{\theta^\ast} (x,t)$를 보장하며, 거의 대부분의 $x$와 $t$에 대해 최적해와 $\nabla_x \log p_t (x)$가 같다.
SMLD와 DDPM에서와 같이 일반적으로
\[\begin{equation} \lambda \propto 1/\mathbb{E} [\| \nabla_{x(t)} \log p_{0t} (x(t) | x(0)) \|_2^2] \end{equation}\]을 선택할 수 있다.
일반적으로 transition kernel $p_{0t} (x(t) \vert x(0))$를 알아야 $\theta^\ast$ 식을 효율적으로 풀 수 있다. $f$가 affine이면 transition kernel은 항상 가우시안 분포이고, 평균과 분산을 closed-form으로 구할 수 있다. 보다 일반적인 SDE의 경우 Kolmogorov’s forward equation을 풀어 $p_{0t} (x(t) \vert x(0))$을 얻을 수 있다. 또는 $p_{0t} (x(t) \vert x(0))$에서 샘플링을 하여 SDE를 시뮬레이션하고 학습 시 denoising score matching 식 대신 sliced score matching으로 대체할 수 있다.
4. Examples: VE, VP SDES and beyond
SMLD와 DDPM에서 사용한 noise pertubation은 서로 다른 SDE의 discretization으로 생각할 수 있다.
총 $N$개의 noise scale을 사용하는 경우, SMLD의 각 pertubation kernel $p_{\sigma_i} (x \vert x_0)$는 다음과 같은 Markov chain에서의 $x_i$의 분포에 대응된다.
\[\begin{equation} x_i = x_{i-1} + \sqrt{\sigma_i^2 - \sigma_{i-1}^2} z_{i-1}, \quad \quad i = 1, \cdots, N \end{equation}\]여기서 $z_{i-1} \sim \mathcal{N}(0, I)$이고, 간략하게 설명하기 위해서 $\sigma_0 = 0$으로 둔다. $N$이 무한대로 갈 때, \(\{\sigma_i\}_{i=1}^N\)은 함수 $\sigma (t)$이 되고 $z_i$는 $z(t)$가 된다. 또한 연속적인 시간 변수 $t \in [0,1]$을 사용하면 Markov chain \(\{x_i\}_{i=1}^N\)은 연속적인 stochastic process \(\{x(t)\}_{t=0}^1\)이 된다. \(\{x(t)\}_{t=0}^1\)은 다음 SDE로 나타낼 수 있다.
\[\begin{equation} dx = \sqrt{\frac{d[\sigma^2 (t)]}{dt}} dw \end{equation}\]DDPM의 pertubation kernel \(\{p_{\alpha_i} (x \vert x_0)\}_{i=1}^N\)도 비슷하게 보면, discrete Markov chain은
\[\begin{equation} x_i = \sqrt{1-\beta_i} x_{i-1} + \sqrt{\beta_i} z_{i-1} \end{equation}\]이고, $N$이 무한대로 갈 때 다음 SDE로 수렴한다.
\[\begin{equation} dx = -\frac{1}{2} \beta(t) x dt + \sqrt{\beta (t)} dw \end{equation}\]따라서, SMLD와 DDPM의 noise pertubation은 SDE의 discretization에 대응된다. SMLD의 SDE는 $t$가 무한대로 갈 때 항상 분산이 무한이 커지고, DDPM의 SDE는 초기 분포에 단위 분산이 있는 경우 분산이 1로 고정된 프로세스를 생성한다. 이런 차이 때문에 SMLD의 SDE는 Variance Exploding (VE) SDE, DDPM의 SDE는 Variance Preserving (VP) SDE라 부른다.
저자들은 VP SDE에서 영감을 받아 likelihood에서 특히 더 잘 수행되는 다음과 같은 새로운 유형의 SDE를 제안하였다.
\[\begin{equation} dx = -\frac{1}{2} \beta(t) x dt + \sqrt{\beta (t) (1-e^{-2 \int_0^t \beta(s) ds})} dw \end{equation}\]동일한 $\beta(t)$를 사용하여 동일한 초기 분포에서 시작하는 경우, 위 식에 의해 유도된 stochastic process의 분산은 항상 모든 timestep에 대하여 VP SDE 내에 있다. 이런 이유 때문에 위 식을 sub-VP SDE이라 부른다.
VE, VP, sub-VP SDE가 모두 affine drift coefficient를 가지기 때문에 각 SDE의 pertubation kernel $p_{0t} (x(t) \vert x(0))$은 모두 가우시안 분포이며 closed-form으로 계산할 수 있다. 이는 학습을 효율적으로 만든다.
Solving the Reverse SDE
1. Reverse Diffusion Sampler
시간에 의존하는 score 기반 모델 $s_\theta$를 학습시킨 후, $s_\theta$를 사용하여 reverse-time SDE를 구성한 다음 수치적 접근 방식으로 시뮬레이션하여 $p_0$에서 생성할 수 있다.
Euler Maruyama나 stochastic Runge-Kutta method와 같은 SDE를 풀기 위한 general-purpose solver를 reverse-time SDE에 적용하여 샘플을 생성할 수 있다. DDPM의 ancestral sampling은 reverse-time VP SDE의 discretization 중 하나에 해당할 뿐이며 다른 discretization으로 더 나은 성능을 얻을 수 있다.
새로운 SDE에 대한 샘플링 규칙을 도출하는 것이 쉽지 않을 수 있다. 저자들은 이를 위해 forward SDE와 동일한 방식으로 reverse-time SDE를 discretize한 reverse diffusion sampler를 제안하며, 이는 forward discretization에서 쉽게 도출할 수 있다.
2. Predictor-Corrector Samplers
논문에서는 numerical SDE solver의 해를 보정하기 위해 score 기반의 MCMC로 $p_t$에서 직접 샘플을 뽑는다.
각 timestep에서 numerical SDE solver가 먼저 다음 timestep의 샘플을 예측하며, 이를 “predictor”라 부른다. 그런 다음 score 기반의 MCMC로 예측된 샘플의 주변 확률 분포를 보정하며, 이를 “corrector”라 부른다. 이런 식의 샘플링 알고리즘을 Predictor-Corrector (PC) Sampler라 부른다.
다음은 PC sampler의 대략적인 알고리즘이다.

다음은 SMLD와 DDPM의 기존의 샘플링 방법을 PC sampler로 일반화한 것이다.

구체적인 Corrector 알고리즘은 다음과 같다.

3. Probability Flow and Connection to Neural ODEs
모든 diffusion process에 대하여, 궤적이 SDE와 같은 주변 확률 밀도 \(\{p_t (x)\}_{t=0}^T\)를 공유하는 deterministic process가 존재한다. 이 deterministic process는 다음 ODE를 만족한다.
\[\begin{equation} dx = \bigg[ f(x,t) - \frac{1}{2} g(t)^2 \nabla_x \log p_t (x) \bigg] dt \end{equation}\]위 식은 score를 아는 경우 SDE에 의해 결정된다. 이 ODE를 probability flow ODE라 부른다. 또한 score function이 신경망에 의해 근사되기 때문에 Neural ODE이다.
위의 ODE를 적분하면 임의의 데이터 포인트 $x(0)$에서 latent space $x(T)$를 인코딩할 수 있다. 디코딩은 대응되는 reverse-time SDE의 ODE를 적분하여 할 수 있다. 샘플링이 deterministic하기 때문에 latent representation을 조작하여 image editing을 할 수 있다.
대부분의 invertible model과 다르게 ODE를 이용한 인코딩은 uniquely identifiable하다. 즉, 충분한 데이터, 모델의 capacity, 최적화의 정확도가 보장된다면 인코딩은 데이터 분포에 유일하게 결정된다. 이는 forward SDE에 학습가능한 파라미터가 존재하지 않으며 완벽하게 추정된 score가 주어지면 probability flow ODE는 동일한 궤적을 제공하기 때문이다.
Neural ODE와 마찬가지로 다양한 최종 조건 $x(T) \sim p_T$에서 ODE를 풀면 $x(0) \sim p_0$를 샘플링할 수 있다. 특히 corrector와 함께 사용할 때 fixed discretization 전략을 사용하면 경쟁력 있는 샘플을 생성할 수 있다. Black-box ODE solver를 사용하면 고품질의 샘플을 생성할 뿐만 아니라 효율성을 위해 정확도를 절충할 수 있다. 더 큰 오차를 허용하면 샘플의 시각적 품질에 영향을 주지 않고 함수 평가 횟수를 90% 이상 줄일 수 있다.
다음은 probability flow ODE로 빠르게 샘플링한 결과이다.

Probability flow ODE는 수치 정밀도가 변화함에 따라 적응형 stepsize로 빠른 샘플링이 가능하고 (왼쪽), 품질을 손상시키지 않고 score function 평가 횟수 (NFE)를 줄이며 (중간), latent에서 이미지로의 가역적 매핑은 interpolation을 허용한다 (오른쪽).
4. Experiments
다음은 CIFAR-10에서 다양한 reverse-time SDE solver를 사용한 결과이다.

P는 predictor만 사용한 경우, C는 corrector만 사용한 경우, PC는 Predictor-Corrector sampler를 사용한 경우이다. P와 C 뒤의 숫자는 사용한 샘플링 step의 수이다.
Reverse diffusion을 사용한 것이 ancestral sampling보다 결과가 좋았으며, probability flow ODE를 사용하였을 떄의 결과가 가장 좋았다. 또한 predictor와 corrector를 모두 사용할 때 결과가 가장 좋았다.
다음은 CIFAR-10에서의 negative log-likelihood를 측정한 결과이다.
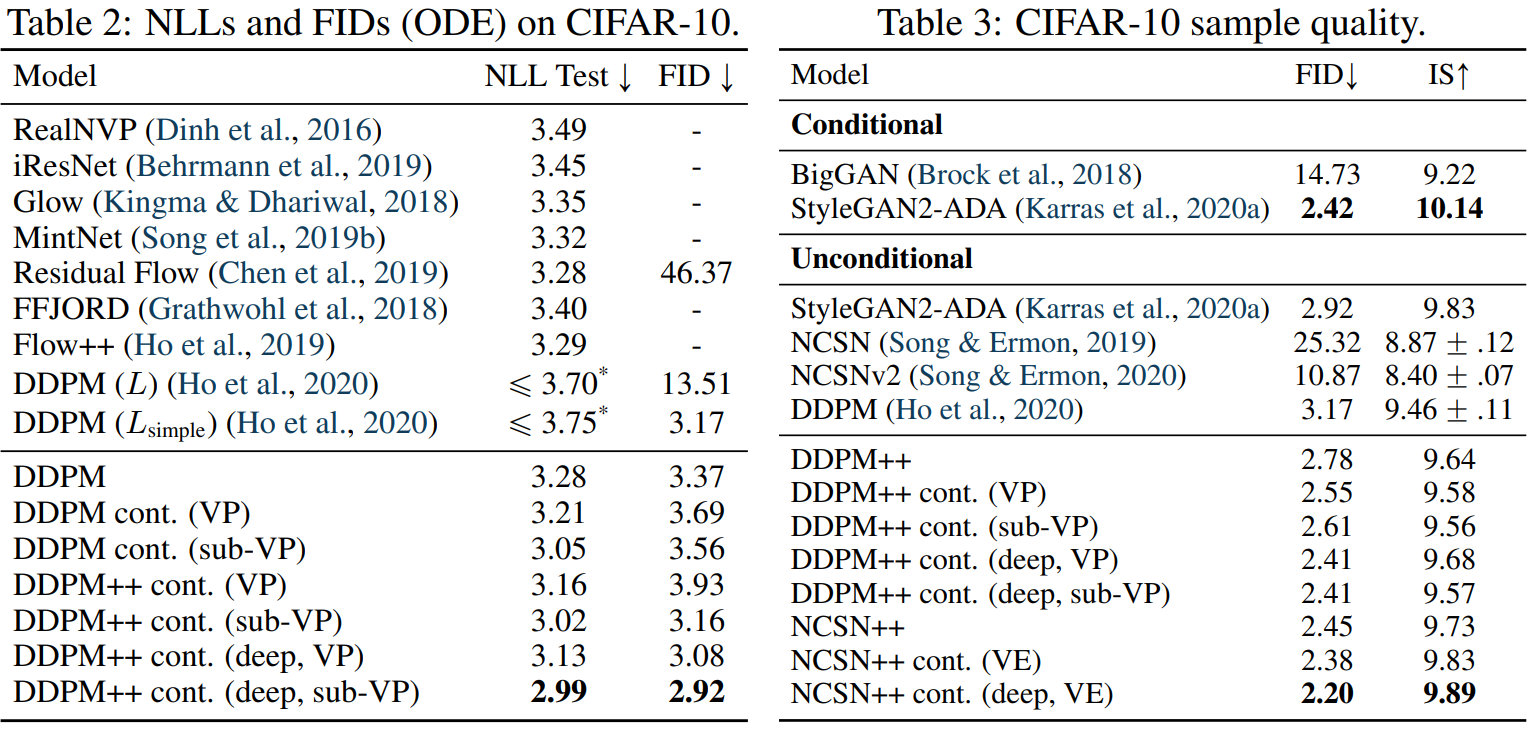
“cont.”는 연속적인 목표 함수를 사용한 것이고 “++”는 개선된 아키텍처이다.
개선된 아키텍처의 세부사항은 다음과 같다.
- Finite Impulse Response (FIR)를 기반으로 한 anti-aliasing으로 upsampling과 downsampling 진행
- 모든 skip connection을 $\frac{1}{\sqrt{2}}$로 rescaling (GAN에서 주로 사용하는 방법)
- 기존 residual block을 BigGAN의 residual block으로 대체
- 각 resolution에 대한 residual block의 개수를 2에서 4로 늘림
- Incorporating progressive growing architectures (StyleGAN-2에서 사용)
- EMA(exponential moving average) rate가 성능에 주요 (VE는 0.999, VP는 0.9999 사용)
Controllable Generation
프레임워크의 연속 구조를 통해 $p_0$에서 데이터 샘플을 생성할 수 있을 뿐만 아니라 $p_t (y \vert x(t))$를 아는 경우 $p_0 (x(0) \vert y)$에서도 샘플을 생성할 수 있다. 주어진 forward SDE에 대하여 conditional reverse-time SDE를 풀면 $p_T (x(T) \vert y)$에서 시작하여 $p_t (x(t) \vert y)$에서 샘플링이 가능하다.
$p_t (x(t) \vert y)$가 $p_t (x(t)) p (y \vert x(t))$에 비례하기 때문에 score $\nabla_x \log p_t (x(t) \vert y)$는 다음 식으로 쉽게 계산할 수 있다.
\[\begin{equation} \nabla_x \log p_t (x(t) \vert y) = \nabla_x \log p_t (x(t)) + \nabla_x \log p (y \vert x(t)) \end{equation}\]따라서 conditional reverse-time SDE는 다음과 같다.
\[\begin{equation} dx = \{ f(x,t) - g(t)^2 [\nabla_x \log p_t (x) + \nabla_x \log p_t (y | x)] \} dt + g(t) d \bar{w} \end{equation}\]$\nabla_x \log p_t (y \vert x)$를 추정할 수 있다면 조건부 샘플링이 가능하다. $\log p_t (y \vert x)$를 학습하는 별도의 모델을 두고 기울기를 계산하는 것도 가능하고, 도메인 지식과 휴리스틱을 이용하여 기울기를 추정할 수도 있다.
다음은 조건부 샘플링의 결과이다.

왼쪽은 32$\times$32 CIFAR-10에서 클래스 조건부 샘플링을 한 결과이다. 위의 4행은 automobile을 조건으로 주었으며 나머지 4행은 horse를 조건으로 주었다. 오른쪽은 256$\times$256 LSUN에서 inpainting (위의 2행)과 colorization (아래 2행)을 한 결과이다. 첫번째 열은 원본 이미지이고 두번째 열은 masked/grayscale 이미지이다. 나머지 열은 샘플링된 결과이다.