[논문리뷰] Segment Any 3D Gaussians

arXiv 2023. [Paper] [Page] [Github]
Jiazhong Cen, Jiemin Fang, Chen Yang, Lingxi Xie, Xiaopeng Zhang, Wei Shen, Qi Tian
AI Institute, SJTU | Huawei Inc.
1 Dec 2023

Introduction

Radiance field에서의 interactive 3D segmentation은 장면 조작, 자동 라벨링, 가상 현실과 같은 다양한 영역에서의 잠재적인 응용으로 인해 연구자들의 많은 관심을 받았다. 이전 방법들은 주로 self-supervised 비전 모델에서 추출한 멀티뷰 2D feature들을 모방하기 위해 feature field를 학습시켜 2D visual feature를 3D 공간으로 끌어올린 다음 3D feature의 유사도를 사용하여 두 점이 동일한 객체에 속하는지 여부를 측정하였다. 이러한 접근 방식은 단순한 segmentation 파이프라인으로 인해 빠르지만, feature에 포함된 정보를 파싱하는 메커니즘(ex. segmentation 디코더)이 부족하기 때문에 segmentation의 세분성(granularity)이 coarse할 수 있다.

대조적으로, 또 다른 패러다임은 멀티뷰의 세분화한 2D segmentation 결과를 3D mask grid에 직접 투영하여 2D segmentation 기반 모델을 3D로 끌어올리는 것이다. 이 접근 방식은 정확한 segmentation 결과를 얻을 수 있지만 foundation model과 볼륨 렌더링을 여러 번 실행해야 하기 때문에 상당한 시간 오버헤드로 인해 사용자와의 상호 작용이 제한된다. 특히 segmentation이 필요한 여러 개체가 포함된 복잡한 장면의 경우 이러한 계산 비용은 감당할 수 없을 정도이다.

위의 논의는 효율성과 정확성을 모두 달성하는 데 있어 현재 기존 패러다임의 딜레마를 드러내며 기존 패러다임의 성능을 제한하는 두 가지 요소이다.

1. Implicit radiance field는 효율적인 segmentation을 방해한다. 즉, 3D 개체를 검색하려면 3D 공간을 통과해야 한다.
2. 2D segmentation 디코더를 활용하면 segmentation 품질은 높지만 효율성은 낮다.

3D Gaussian Splatting(3DGS)는 고품질 및 실시간 렌더링 능력으로 인해 게임 체인저가 되었다. 3DGS는 3D 장면을 표현하기 위해 색이 있는 3D Gaussian 집합을 채택하였다. 이러한 Gaussian의 평균은 3D 공간에서의 위치를 나타내므로 3DGS는 일종의 포인트 클라우드로 볼 수 있다. 이는 광범위하고 종종 비어 있는 3D 공간의 광범위한 처리를 우회하는 데 도움이 되며 풍부한 명시적 3D prior를 제공한다. 이러한 포인트 클라우드와 같은 구조를 통해 3DGS는 효율적인 렌더링을 실현할 뿐만 아니라 segmentation task에 이상적인 후보가 되었다.

본 논문은 3DGS를 기반으로 2D segmentation foundation model (즉, Segment Anything Model)의 세분화된 segmentation 능력을 3D Gaussian으로 추출할 것을 제안하였다. 이 전략은 2D visual feature를 3D로 끌어올리는 데 중점을 두고 세밀한 3D segmentation을 가능하게 하는 이전 방법에서 벗어났다. 또한 inference 중에 2D segmentation model을 여러번 실행하여 시간이 많이 걸리는 것을 방지한다. 추출은 Segment Anything Model(SAM)을 사용하여 자동으로 추출된 마스크를 기반으로 Gaussian에 대한 3D feature를 학습시켜 수행된다. Inference 중에 입력 프롬프트를 사용하여 일련의 쿼리가 생성된 다음 효율적인 feature matching을 통해 예상되는 Gaussian을 검색하는 데 사용된다.

본 논문의 접근 방식인 Segment Any 3D GAussians (SAGA)는 밀리초 단위로 세밀한 3D segmentation을 달성하고 포인트, 낙서, 마스크를 포함한 다양한 종류의 프롬프트를 지원할 수 있다. 기존 벤치마크에 대한 평가는 SAGA의 segmentation 품질이 이전 SOTA 기술과 동등하다. 특히 Gaussian feature 학습은 일반적으로 5~10분 내에 완료된다.

Methodology

1. Preliminaries

• 3D Gaussian Splatting (3DGS)
• Segment Anything Model (SAM)

2. Overall Pipeline

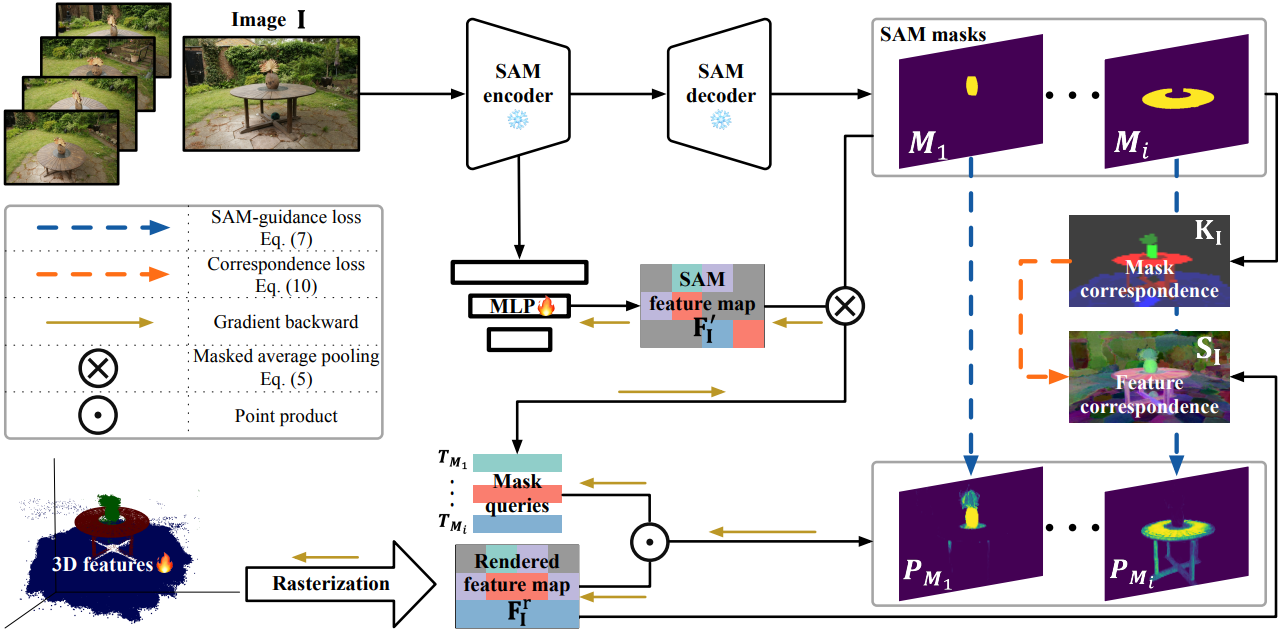
위 그림에서 볼 수 있듯이 사전 학습된 3DGS 모델 $\mathcal{G}$와 해당 학습 세트 $\mathcal{I}$가 주어지면 먼저 SAM 인코더를 사용하여 2D feature map \(\mathbf{F}_\mathbf{I}^\textrm{SAM} \in \mathbb{R}^{C^\textrm{SAM} \times H \times W}\)와 $\mathcal{I}$의 각 이미지 $\mathbf{I} \in \mathbb{R}^{H \times W}$에 대해 여러 세분성을 가진 마스크들의 집합을 추출한다. 그런 다음 추출된 마스크를 기반으로 $\mathcal{G}$의 각 Gaussian $\mathbf{g}$에 대해 저차원 feature \(\mathbf{f}_\mathbf{g} \in \mathbb{R}^C\)를 학습시켜 여러 뷰 사이에 일관성 있는 다중 세분성 (multi-granularity) 분할 정보를 집계한다. 여기서 $C$는 feature 차원을 나타내며 기본값은 32로 설정된다. 이는 신중하게 설계된 SAM-guidance loss를 통해 달성된다. Feature의 압축성을 더욱 향상시키기 위해 추출된 마스크에서 point-wise correspondence들을 도출하고 이를 feature로 증류(distill)한다 (즉, correspondence loss).

Inference 단계에서는 카메라 포즈가 $v$인 특정 뷰에 대해 입력 프롬프트 $\mathcal{P}$를 기반으로 일련의 쿼리 $\mathcal{Q}$가 생성된다. 그런 다음 이러한 쿼리는 학습된 feature와 효율적인 feature matching을 통해 해당 대상의 3D Gaussian을 검색하는 데 사용된다. 또한 검색된 3D Gaussian을 개선하기 위해 3DGS의 포인트 클라우드형 구조가 제공하는 강력한 3D prior를 활용하는 효율적인 후처리 연산도 도입한다.

3. Training Features for Gaussians

특정 카메라 포즈 $v$에 대한 학습 이미지 $\mathbf{I}$가 주어지면 먼저 사전 학습된 3DGS 모델 $\mathcal{G}$에 따라 해당 feature map을 렌더링한다. 픽셀 $p$의 렌더링된 feature \(\mathbf{F}_{\mathbf{I}, p}^r\)은 다음과 같이 계산된다.

\[\begin{equation} \mathbf{F}_{\mathbf{I}, p}^r = \sum_{i \in \mathcal{N}} \mathbf{f}_i \alpha_i \prod_{j=1}^{i-1} (1 - \alpha_j) \end{equation}\]

여기서 $\mathcal{N}$은 픽셀과 겹치는 정렬된 Gaussian 집합이다. 학습 단계에서는 새로 첨부된 feature들을 제외한 3D 가우스 Gaussian의 다른 모든 속성 (ex. 평균, 공분산, 불투명도)을 고정한다.

SAM-guidance Loss

SAM을 통해 자동으로 추출된 2D 마스크 \(\mathcal{M}_\mathbf{I}\)는 복잡하고 혼잡하다. 즉, 3D 공간의 한 점이 서로 다른 뷰에서 서로 다른 개체/부분으로 분할될 수 있다. 이러한 모호한 supervision 신호는 3D feature들을 처음부터 학습하는 데 큰 어려움을 초래한다. 이 문제를 해결하기 위해 저자들은 SAM에서 생성된 feature들을 guidance로 사용할 것을 제안하였다. 먼저 MLP $\phi$를 채택하여 SAM feature들을 3D feature와 동일한 저차원 공간에 투영한다.

\[\begin{equation} \mathbf{F}_\mathbf{I}^\prime = \phi (\mathbf{F}_\mathbf{I}^\textrm{SAM}) \end{equation}\]

그런 다음 $\mathcal{M}_\mathbf{I}^\textrm{SAM}$에서 추출된 각 마스크 $\mathbf{M}$에 대해 masked average pooling 연산을 통해 쿼리 \(\mathbf{T}_\mathbf{M} \in \mathbb{R}^C\)를 얻는다.

\[\begin{equation} \mathbf{T}_\mathbf{M} = \frac{1}{\| \mathbf{M} \|_1} \sum_{p=1}^{HW} \unicode{x1D7D9} (\mathbf{M}_p = 1) \mathbf{F}_{\mathbf{I},p}^\prime \end{equation}\]

여기서 $\unicode{x1D7D9}$은 indicator function이다. 그런 다음 \(\mathbf{T}_\mathbf{M}\)은 softmaxed point product을 통해 렌더링된 feature map \(\mathbf{F}_\mathbf{I}^r\)을 분할하는 데 사용된다.

\[\begin{equation} \mathbf{P}_\mathbf{M} = \sigma (\mathbf{T}_\mathbf{M} \cdot \mathbf{F}_\mathbf{I}^r) \end{equation}\]

여기서 $\sigma$는 element-wise sigmoid function이다. SAM-guidance loss는 segmentation 결과 \(\mathbf{P}_\mathbf{M}\)과 대응되는 SAM 추출 마스크 $\mathbf{M}$ 사이의 binary cross entropy로 정의된다.

\[\begin{equation} \mathcal{L}_\textrm{SAM} = - \sum_{\mathbf{I} \in \mathcal{I}} \sum_{\mathbf{M} \in \mathcal{M}_\mathbf{I}} \sum_p^{HW} [\mathbf{M}_p \log \mathbf{P}_{\mathbf{M}, p} + (1 - \mathbf{M}_p) \log (1 - \mathbf{P}_{\mathbf{M}, p})] \end{equation}\]

Correspondence Loss

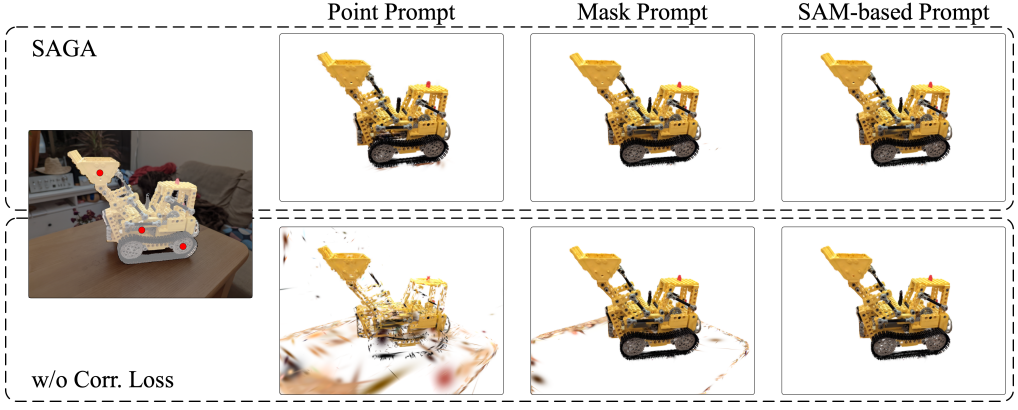
실제로 저자들은 SAM-guidance loss를 통해 학습된 feature가 충분히 작지 않아 다양한 종류의 프롬프트의 segmentation 품질이 저하된다는 것을 발견했다. 따라서 contrastive correspondence distillation 방법에서 영감을 받아 문제를 해결하기 위해 correspondence loss를 도입하였다.

앞서 언급한 바와 같이 각 이미지 $\mathbf{I}$에 대해 마스크 세트 $\mathcal{M}_\mathbf{I}$가 SAM을 통해 추출된다. $\mathbf{I}$의 두 픽셀 $p_1$, $p_2$를 고려하면 \(\mathcal{M}_\mathbf{I}\)의 여러 마스크에 속할 수 있다. \(\mathcal{M}_\mathbf{I}^{p_1}\)와 \(\mathcal{M}_\mathbf{I}^{p_2}\)를 각각 $p_1$과 $p_2$가 각각 속하는 마스크들이라 하자. 직관적으로 두 집합의 IoU(intersection over union)가 더 크면 두 픽셀은 더 유사한 feature들을 공유해야 한다. 따라서 mask correspondence \(\mathbf{K}_\mathbf{I}(p_1, p_2)\)는 다음과 같이 정의된다.

\[\begin{equation} \mathbf{K}_\mathbf{I}(p_1, p_2) = \frac{\vert \mathcal{M}_\mathbf{I}^{p_1} \cap \mathcal{M}_\mathbf{I}^{p_2} \vert}{\vert \mathcal{M}_\mathbf{I}^{p_1} \cup \mathcal{M}_\mathbf{I}^{p_2} \vert} \end{equation}\]

두 픽셀 $p_1$, $p_2$ 사이의 feature correspondences \(\mathbf{S}_\mathbf{I} (p_1, p_2)\)는 렌더링된 feature 사이의 코사인 유사도로 정의된다.

\[\begin{equation} \mathbf{S}_\mathbf{I} (p_1, p_2) = \langle \mathbf{F}_{\mathbf{I}, p_1}^r, \mathbf{F}_{\mathbf{I}, p_2}^r \rangle \end{equation}\]

그러면 correspondence loss는 다음과 같이 정의된다.

\[\begin{equation} \mathcal{L}_\textrm{corr} = -\sum_{\mathbf{I} \in \mathcal{I}} \sum_{p_1}^{HW} \sum_{p_2}^{HW} \mathbf{K}_\mathbf{I} (p_1, p_2) \mathbf{S}_\mathbf{I} (p_1, p_2) \end{equation}\]

두 픽셀이 동일한 세그먼트에 속하지 않는 경우 \(\mathbf{K}_\mathbf{I}\)의 값이 0인 entry를 -1로 설정하여 feature 유사도를 줄인다.

SAM-guidance loss와 correspondence loss의 두 가지 구성 요소를 사용한 SAGA의 최종 loss는 다음과 같다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{SAM} + \lambda \mathcal{L}_\textrm{corr} \end{equation}\]

여기서 $\lambda$는 두 loss 항의 균형을 맞추기 위한 hyperparameter이다. (기본값은 1)

4. Inference

학습은 렌더링된 feature map에서 수행되지만 rasterization 연산의 선형성은 3D 공간의 feature가 이미지 평면의 렌더링된 feature와 정렬되도록 보장한다. 따라서 2D에서 렌더링된 feature들을 사용하여 3D Gaussian의 segmentation을 할 수 있다. 이러한 특성은 SAGA에 포인트, 낙서, 마스크를 포함한 다양한 종류의 프롬프트와의 호환성을 부여한다. 또한, 3DGS에서 제공하는 3D prior 기반의 효율적인 후처리 알고리즘을 도입한다.

Point Prompt

특정 뷰 $v$에 대해 렌더링된 feature map \(\mathbf{F}_v^r\)에서 해당 feature를 직접 검색하여 positive point들과 negative point들에 대한 쿼리를 생성한다. \(\mathcal{Q}_v^p\)와 \(\mathcal{Q}_v^n\)을 각각 $N_p$개의 positive query와 $N_n$개의 negative query라고 하자. 3D Gaussian $\mathbf{g}$에 대하여 positive score \(S_\mathbf{g}^p\)는 해당 feature $\mathbf{f}_\mathbf{g}$와 positive query \(\mathcal{Q}_v^p\) 사이의 코사인 유사도의 최대값, 즉

\[\begin{equation} S_\mathbf{g}^p = \max \{\langle \mathbf{f}_\mathbf{g}, \mathbf{Q}^p \rangle \; \vert \; \mathbf{Q}^p \in \mathcal{Q}_v^p \} \end{equation}\]

로 정의된다. 마찬가지로, negative score는

\[\begin{equation} S_\mathbf{g}^n = \max \{\langle \mathbf{f}_\mathbf{g}, \mathbf{Q}^n \rangle \; \vert \; \mathbf{Q}^n \in \mathcal{Q}_v^n \} \end{equation}\]

로 정의된다. 3D Gaussian은 \(S_\mathbf{g}^p > S_\mathbf{g}^n\)인 경우에만 타겟 $\mathcal{G}^t$에 속한다.

Noisy Gaussian을 추가로 필터링하기 위해 적응형 threshold $\tau$가 positive score로 설정된다. 즉, \(S_\mathbf{g}^p > \tau\)인 경우에만 $\mathbf{g} \in \mathcal{G}^t$이다. $\tau$는 positive score 최대값의 평균으로 설정된다. 이러한 필터링으로 인해 많은 false negative들이 발생할 수 있지만 나중에 설명할 후처리를 통해 해결할 수 있다.

Mask And Scribble Prompts

단순히 dense한 프롬프트를 여러 포인트로 처리하면 감당할 수 없는 GPU 메모리 오버헤드가 발생한다. 따라서 K-means 알고리즘을 사용하여 dense한 프롬프트에서 일부 positive query와 negative query를 추출한다. K-means의 클러스터 수는 경험적으로 5개로 설정되어 있지만 대상 객체의 복잡도에 따라 조정 가능하다.

SAM-based Prompt

이전 프롬프트들은 렌더링된 feature map에서 가져온다. SAM-guidance loss를 사용하면 쿼리 생성을 위해 저차원 SAM feature \(\mathbf{F}_v^\prime\)를 직접 사용할 수 있다. 정확한 2D segmentation 결과 \(\mathbf{M}_v^\textrm{ref}\)를 생성하기 위해 입력 프롬프트가 먼저 SAM에 공급된다. 이 2D 마스크를 사용하여 먼저 masked average pooling을 사용하여 쿼리 \(\mathbf{Q}^\textrm{mask}\)를 얻고 이 쿼리를 사용하여 2D 렌더링된 feature map \(\mathbf{F}_v^r\)를 분할하여 임시 2D 분할 마스크 \(\mathbf{M}_v^\textrm{temp}\)를 얻은 다음 \(\mathbf{M}_v^\textrm{ref}\)와 비교한다. \(\mathbf{M}_v^\textrm{temp}\)와 \(\mathbf{M}_v^\textrm{ref}\)의 교차 영역이 \(\mathbf{M}_v^\textrm{ref}\)의 큰 부분(기본적으로 90%)을 차지하면 \(\mathbf{Q}_v^\textrm{mask}\)가 쿼리로 받아들여진다. 그렇지 않으면 K-means 알고리즘을 사용하여 마스크 내의 저차원 SAM feature \(\mathbf{F}_v^\prime\)에서 다른 쿼리 집합 \(\mathcal{Q}_v^\textrm{kmeans}\)를 추출한다. Segmentation 대상에는 단순히 masked average pooling을 적용하여 캡처할 수 없는 많은 구성 요소가 포함될 수 있으므로 이러한 전략을 채택하였다고 한다.

쿼리 집합 \(\mathcal{Q}_v^\textrm{SAM} = \{\mathbf{Q}_v^\textrm{mask}\}\) 또는 \(\mathcal{Q}_v^\textrm{SAM} = \mathcal{Q}_v^\textrm{kmeans}\)를 얻은 후 이후의 프로세스는 이전 프롬프트 접근 방식과 거의 동일하다. SAM-guidance loss와 일치하도록 segmentation을 위한 메트릭으로 코사인 유사도 대신 내적을 사용한다. 3D Gaussian $\mathbf{g}$의 경우 positive score \(S_\mathbf{g}^p\)는 다음과 같이 내적의 최대값으로 정의된다.

\[\begin{equation} S_\mathbf{g}^p = \max \{ \mathbf{f}_\mathbf{g} \cdot \mathbf{Q} \; \vert \; \mathbf{Q} \in \mathcal{Q}_v^\textrm{SAM} \} \end{equation}\]

3D Gaussian $\mathbf{g}$는 positive point가 모든 score \(\mathcal{S}_\mathcal{G} = \{S_\mathbf{g}^p \vert \mathbf{g} \in \mathcal{G}\}\)의 평균과 표준 편차의 합인 또다른 적응형 threshold $\tau^\textrm{SAM}$보다 큰 경우 segmentation 타겟 $\mathcal{G}^t$에 속한다.

5. 3D Prior Based Post-processing

3D Gaussian의 초기 segmentation $\mathcal{G}^t$는 두 가지 주요 문제가 있다.

1. 불필요한 noisy Gaussian의 존재
2. 대상 객체에 필수적인 특정 Gaussian의 생략

이 문제들을 해결하기 위해 통계적 필터링과 region growing을 포함한 전통적인 포인트 클라우드 segmentation 기술을 활용한다. 포인트 프롬프트와 낙서 프롬프트를 기반으로 한 segmentation의 경우 noisy Gaussian을 필터링하기 위해 통계적 필터링이 사용된다. 마스크 프롬프트와 SAM 기반 프롬프트의 경우 2D 마스크는 검증된 Gaussian 집합을 얻기 위해 $\mathcal{G}^t$에 투영되고 원하지 않는 Gaussian을 제외하기 위해 $\mathcal{G}$에 투영된다. 결과적으로 검증된 Gaussian들는 region growing 알고리즘의 시드 역할을 한다. 마지막으로, ball query 기반 region growing 방법을 적용하여 원본 모델 $\mathcal{G}$에서 필요한 모든 Gaussian들을 검색한다.

Statistical Filtering

두 Gaussian 사이의 거리는 동일한 대상에 속하는지 여부를 나타낼 수 있다. 통계적 필터링은 K-Nearest Neighbors(KNN) 알고리즘을 사용하여 $\mathcal{G}^t$ 내의 가장 가까운 $\sqrt{\vert \mathcal{G}^t \vert}$개의 각 Gaussian에 대한 평균 거리를 계산한다. 이어서, $\mathcal{G}^t$의 모든 Gaussian에 대한 평균 거리의 평균 $\mu$와 표준 편차 $\sigma$를 계산한다. 그런 다음 $\mathcal{G}^{t \prime}$을 얻기 위해 $\mu + \sigma$를 초과하는 평균 거리를 갖는 Gaussian들을 제거한다.

Region Growing Based Filtering

마스크 프롬프트 또는 SAM 기반 프롬프트의 2D 마스크는 대상을 정확하게 localizing하기 위한 prior 역할을 할 수 있다. 처음에는 $\mathcal{G}^t$에 마스크를 투영하여 검증된 Gaussian들의 부분집합 $\mathcal{G}^c$를 생성한다. 이어서, $\mathcal{G}^c$ 내의 각 Gaussian $\mathbf{g}$에 대해 동일한 부분집합에서 nearest neighbor까지의 유클리드 거리 \(d_\mathbf{g}\)를 계산한다.

\[\begin{equation} d_\mathbf{g}^{\mathcal{G}^c} = \min \{ D (\mathbf{g}, \mathbf{g}^\prime) \; \vert \; \mathbf{g}^\prime \in \mathcal{G}^c\} \end{equation}\]

여기서 $D(\cdot, \cdot)$는 유클리드 거리이다. 그런 다음 거리가 \(\max \{ d_\mathbf{g}^{\mathcal{G}^c} \vert \mathbf{g} \in \mathcal{G}^c \}\) 보다 작은 이웃 Gaussian들을 $\mathcal{G}^t$에 반복적으로 통합한다. 새로운 Gaussian들이 기준을 충족하지 않아 영역이 수렴되면서 필터링된 segmentation 결과 $\mathcal{G}^{t \prime}$을 얻는다.

포인트 프롬프트와 낙서 프롬프트도 대상을 대략적으로 찾을 수 있지만 이를 기반으로 영역을 성장시키는 데는 시간이 많이 걸린다. 따라서 마스크를 사용할 수 있는 경우에만 region growing 기반 필터링을 적용한다.

Ball Query Based Growing

필터링된 segmentation 출력 $\mathcal{G}^{t \prime}$은 타겟에 속하는 모든 Gaussian들을 포함하지 않을 수 있다. 이 문제를 해결하기 위해 ball query 알고리즘을 활용하여 모든 Gaussian $\mathcal{G}$에서 필요한 모든 Gaussian들을 검색한다. 구체적으로 $\mathcal{G}^{t \prime}$의 각 Gaussian들을 중심으로 반경 $r$에서 이웃을 확인한다. $\mathcal{G}$의 이러한 구형 경계 내에 위치한 Gaussian들을 최종 segmentation 결과 $\mathcal{G}^s$로 집계된다. 반경 $r$은 $\mathcal{G}^{t \prime}$에서 nearest neighbor 거리의 최대값으로 설정된다.

\[\begin{equation} r = \max \{ d_\mathbf{g}^{\mathcal{G}^{t \prime}} \; \vert \; \mathbf{g} \in \mathcal{G}^{t \prime} \} \end{equation}\]

Experiments

• 데이터셋: Neural Volumetric Object Selection (NVOS), SPIn-NeRF, LERF, LLFF, MIP-360

1. Quantitative Results

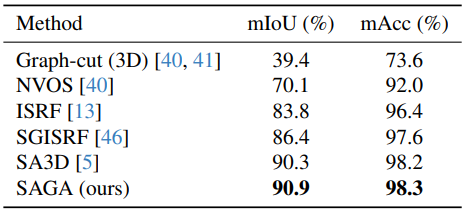
다음은 NVOS에서 정량적으로 비교한 표이다.

다음은 SPIn-NeRF에서 정량적으로 비교한 표이다.

다음은 LERF-figurines에서 SA3D과 비교한 표이다.

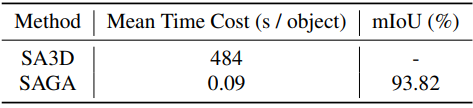
2. Qualitative Results

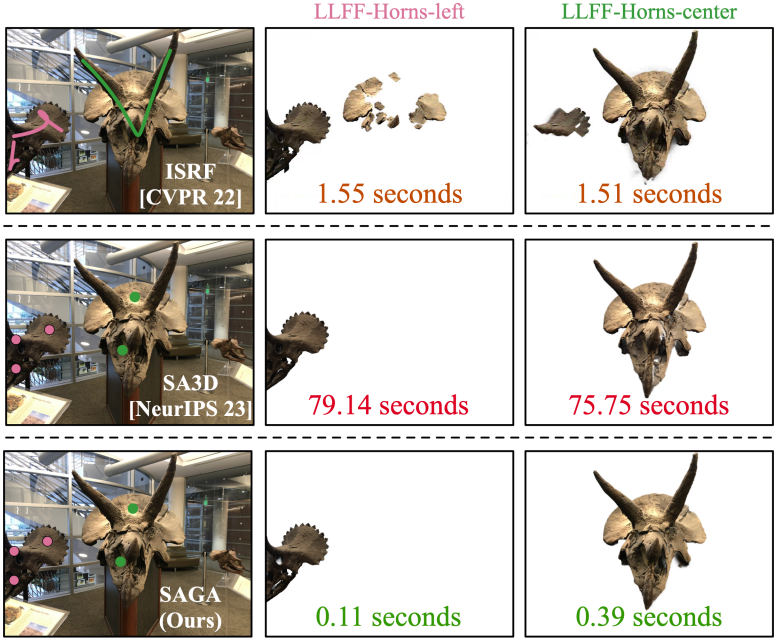
다음은 SAGA의 정성적 결과들이다.

다음은 SAGA의 failure case이다. 오른쪽 위가 segmentation 결과이며 아래는 3DGS 모델의 Gaussian들의 평균을 나타낸 것이다.

이 failure는 3DGS에서 학습된 Gaussian들의 잘못된 기하학적 구조로 인해 발생한다.

3. Ablation Study

다음은 loss 항에 대한 ablation 결과이다.

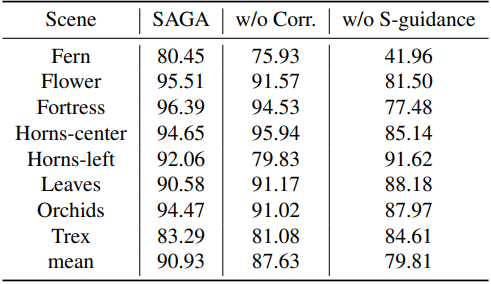
다음은 correspondence loss에 대한 ablation 결과이다.

다음은 후처리에 대한 ablation 결과이다.

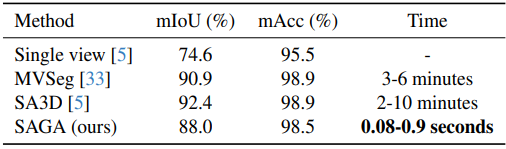
다음은 계산량을 분석한 표이다.

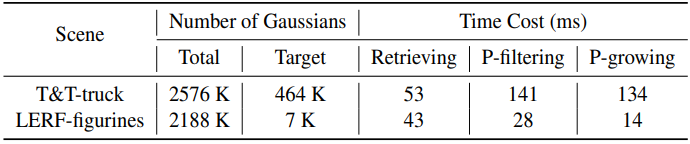
Limitation

1. 3DGS로 학습된 Gaussian들은 형상에 대한 제약 없이 모호하다. 하나의 Gaussian은 여러 객체에 해당할 수 있으므로 feature matching을 통해 개별 객체를 정확하게 분할하는 task가 복잡해진다.
2. SAM에 의해 자동으로 추출된 마스크는 multi-granularity 특성의 부산물로 일정 수준의 잡음이 존재하는 경향이 있다.
3. 후처리 단계는 semantic에 구애받지 않으며 이는 segmentation 결과에 몇몇 false positive point들을 가져온다.