[논문리뷰] s1: Simple test-time scaling
arXiv 2025. [Paper] [Github]
Niklas Muennighoff, Zitong Yang, Weijia Shi, Xiang Lisa Li, Li Fei-Fei, Hannaneh Hajishirzi, Luke Zettlemoyer, Percy Liang, Emmanuel Candès, Tatsunori Hashimoto
Stanford University | University of Washington | Allen Institute for AI | Contextual AI
31 Jan 2025
Introduction
지난 몇 년 동안 언어 모델의 성능 향상은 주로 학습 시간의 컴퓨팅을 scaling하는 데 의존했다. 이러한 강력한 모델의 생성은 이를 기반으로 구축된 새로운 scaling 패러다임인 test-time scaling을 위한 토대를 마련했다. 이 패러다임의 실행 가능성은 최근 OpenAI o1에 의해 검증되었다. OpenAI는 그들의 접근 방식을 상당한 양의 데이터를 사용하는 것을 의미하는 대규모 강화 학습을 사용하는 것으로 설명한다. DeepSeek R1은 수백만 개의 샘플과 여러 학습 단계를 통해 강화 학습을 사용하여 o1 수준의 성능을 성공적으로 복제했다. 그러나 아무도 o1의 명확한 test-time scaling 동작을 공개적으로 복제하지 못했다.
본 논문은 next-token prediction을 사용하여 1,000개 샘플에 대해서만 학습하고 budget forcing이라고 부르는 간단한 test-time 기술을 통해 사고 기간을 제어하면 더 많은 test-time 컴퓨팅으로 성능이 scaling되는 강력한 추론 모델이 생성됨을 보여준다. 구체적으로, 저자들은 s1K를 구성하였는데, 이는 Gemini Thinking Experimental에서 추출한 추론 과정과 답변이 포함된 1,000개의 신중하게 선별된 질문들로 이루어져 있다.
저자들은 16개의 H100 GPU에서 26분만 학습하면 되는 소규모 데이터셋에서 기존 사전 학습된 모델의 supervised fine-tuning (SFT)을 수행하였다. 학습 후 budget forcing을 사용하여 모델이 사용하는 test-time 컴퓨팅의 양을 제어한다.
- 모델이 원하는 한도보다 많은 사고 토큰을 생성하는 경우, end-of-thinking 토큰을 추가하여 강제로 사고 프로세스를 종료한다. 이런 방식으로 사고를 종료하면 모델이 답변을 생성하는 단계로 전환된다.
- 모델이 문제에 대한 test-time 계산을 더 많이 하기를 원한다면, end-of-thinking 토큰의 생성을 억제하고 대신 모델의 현재 추론 과정에 “Wait”을 추가하여 더 많은 탐색을 장려한다.
이 간단한 레시피를 갖춘 본 논문의 모델 s1-32B는 test-time scaling을 보여준다. 또한, s1-32B는 가장 샘플 효율적인 추론 모델이며 OpenAI의 o1-preview보다 성능이 뛰어나다.
저자들은 1,000개의 추론 샘플을 선택할 때 품질, 난이도, 다양성에 대한 metric을 선택 알고리즘에 통합하는 것이 중요하다는 것을 알게 되었다. s1K를 포함한 전체 5.9만 개의 예제 데이터로 학습하더라도, s1K만 사용할 때보다 실질적인 이점이 크지 않다. 이는 신중한 데이터 선택의 중요성을 강조한다.
또한 저자들은 test-time scaling 방법에 대한 요구 사항을 정의하여 다양한 방법을 비교하였으며, budget forcing은 완벽한 제어 가능성과 명확한 양의 기울기로 강력한 성능을 제공하기 때문에 최상의 scaling으로 이어진다.
Reasoning data curation to create s1K
1. Initial collection of 59K samples
저자들은 세 가지 원칙에 따라 초기 59,029개의 질문을 수집하였다.
- 품질: 데이터셋은 고품질이어야 한다. (ex. 형식이 좋지 않은 데이터셋은 무시)
- 난이도: 데이터셋은 도전적이어야 하며 상당한 추론 노력을 필요로 해야 한다.
- 다양성: 데이터셋은 다양한 추론 task를 다루기 위해 다양한 분야에서 유래해야 한다.
저자들은 기존 14개의 데이터셋들에서 총 58,824개의 질문을 수집하였으며, 기존 데이터셋을 보완하기 위해 두 개의 새로운 데이터셋인 s1-prob와 s1-teasers를 만들었다. 전체 데이터 분포는 아래 표와 같다.
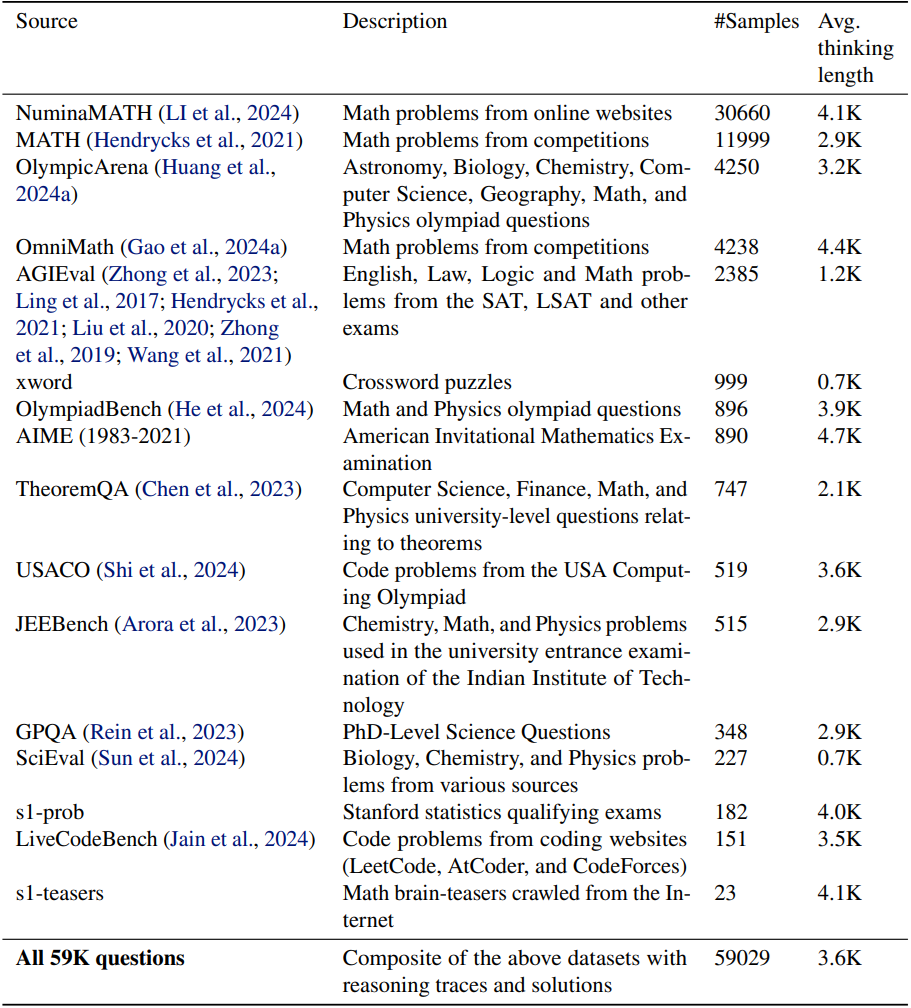
s1-prob은 스탠포드 대학 통계학과 박사 자격 시험의 확률 섹션에서 나온 182개의 질문과 어려운 증명을 다루는 필기 솔루션으로 구성되어 있다. 해당 자격 시험은 매년 치러지며 전문가 수준의 수학적 문제 해결 능력이 요구된다. s1-teasers는 s1-teasers는 퀀트 트레이딩 면접에서 흔히 사용되는 23개의 어려운 두뇌 게임 문제로 구성되어 있다. 각 샘플은 PuzzledQuant에서 가져온 문제와 솔루션으로 구성되어 있으며, 가장 높은 난이도인 Hard의 문제만 선택한 것이다.
저자들은 각 질문에 대해 Google Gemini Flash Thinking API를 사용하여 추론 과정과 응답을 추출하였다. 이를 통해 질문, 생성된 추론 과정, 생성된 솔루션의 triplet 5.9만 개가 생성되었다.
2. Final selection of 1K samples
5.9만 개의 질문 풀에서 직접 학습할 수 있지만, 본 논문의 목표는 최소한의 리소스로 가장 간단한 접근 방식을 찾는 것이다. 따라서 저자들은 3단계의 필터링을 품질, 난이도, 다양성에 따라 1,000개의 샘플을 선별하였다.
품질
먼저 API 오류가 발생한 질문을 모두 제거하여 데이터셋을 54,116개로 줄였다. 다음으로 서식 문제가 있는 문자열 패턴이 포함되어 있는지 확인하여 품질이 낮은 예제를 필터링하여 데이터셋을 51,581개 샘플로 줄였다. 저자들은 이 데이터 풀에서 추가 필터링이 필요 없다고 판단된 고품질 데이터셋에서 384개의 샘플을 추출하였다.
난이도
난이도의 경우 모델 성능과 추론 과정의 길이라는 두 가지 지표를 사용한다. 각 문제에 대해 Qwen2.5-7B-Instruct와 Qwen2.5-32B-Instruct라는 두 가지 모델을 평가하고, Claude 3.5 Sonnet에서 각 시도를 정답과 비교하여 정확성을 평가한다. 더 어려운 문제일수록 더 많은 사고 토큰이 필요하다는 가정에 근거하여, Qwen2.5 tokenizer를 사용하여 각 추론 과정의 토큰 길이를 측정하여 문제 난이도를 나타낸다.
채점 결과에 따라 두 모델 중 하나라도 올바르게 풀 수 있어서 너무 쉬울 수 있는 문제를 제거한다. 두 가지 모델을 사용하는 것은 모델이 쉬운 문제에서 실수하여 쉬운 문제가 필터링되지 않을 수 있기 때문이다. 이렇게 하면 총 샘플이 24,496개로 줄어든다.
다양성
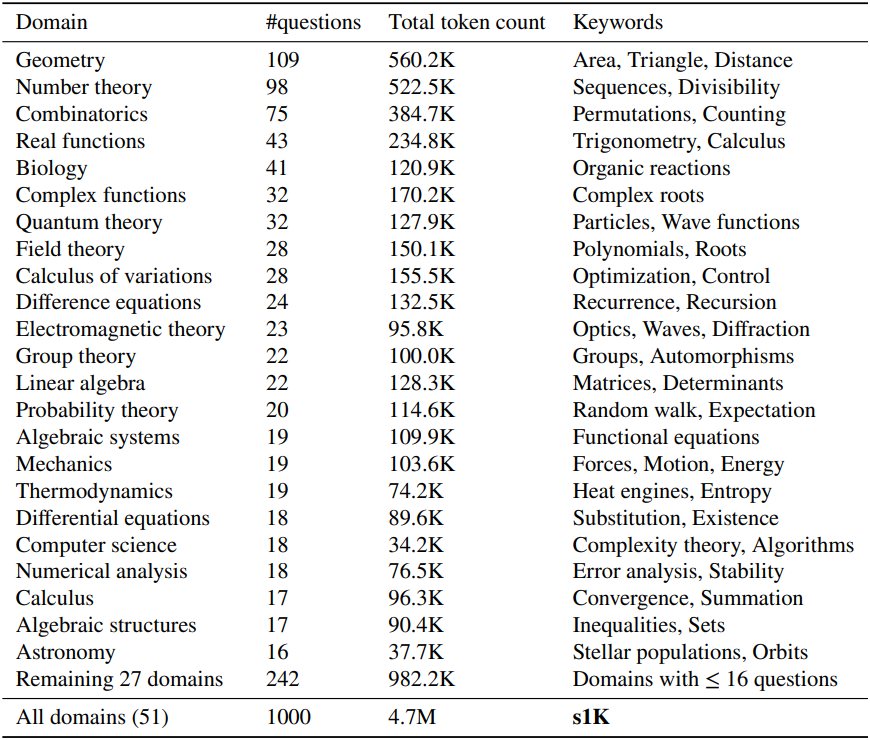
저자들은 다양성을 정량화하기 위해 Claude 3.5 Sonnet을 사용하여 각 질문을 American Mathematical Society의 수학 과목 분류(MSC) 시스템을 기반으로 특정 도메인으로 분류한다. 분류법은 수학 주제에 초점을 맞추지만 생물학, 물리학, 경제학과 같은 다른 과학도 포함한다. 24,496개의 질문 풀에서 최종 예제를 선택하기 위해 먼저 하나의 도메인을 무작위로 균일하게 선택한다. 그런 다음 더 긴 추론 과정을 선호하는 분포에 따라 이 도메인에서 하나의 문제를 샘플링한다. 총 샘플이 1,000개가 될 때까지 이 프로세스를 반복한다.
아래 표에서 볼 수 있드시, 이 3단계 프로세스는 50개의 서로 다른 도메인에 걸친 데이터셋을 생성한다. 세 가지 기준을 조합하여 사용하는 것이 중요하며, 셋 중 하나에만 의존하면 더 나쁜 데이터셋이 생성된다.
Test-time scaling
1. Method
저자들은 test-time scaling 방법을 두 가지로 분류하였다.
- Sequential scaling: 나중의 계산이 이전 계산에 의존하는 경우 (ex. 긴 추론 과정)
- Parallel scaling: 계산이 독립적으로 실행되는 경우 (ex. 다수결 투표)
저자들은 sequential scaling에 집중하였는데, 나중의 계산이 중간 결과를 기반으로 구축될 수 있기 때문에 더 깊은 추론과 반복적 정제가 가능하고, 따라서 더 나은 scaling이 가능하기 때문이다. 저자들은 새로운 sequential scaling 방법과 이를 벤치마킹하는 방법을 제안하였다.
Budget forcing

저자들은 test-time에 최대 또는 최소 사고 토큰 수를 강제로 지정하는 간단한 디코딩 개입을 제안하였다. 구체적으로, end-of-thinking 토큰과 "Final Answer:"을 추가하여 최대 토큰 수를 강제로 지정하여 사고 단계를 조기에 종료하고 모델이 현재 최상의 답변을 제공하도록 한다. 최소 토큰 수를 강제로 지정하기 위해, end-of-thinking 토큰의 생성을 억제하고 선택적으로 모델의 현재 추론 과정에 “Wait”을 추가하여 모델이 현재 생성을 반영하도록 한다.
Baseline
저자들은 다음과 같은 여러 test-time scaling 방법으로 budget forcing을 벤치마킹하였다.
- 조건부 길이 제어 방법: 프롬프트에서 모델에게 생성 길이를 지정하는 방식에 의존한다.
- (a) Token-conditional control: 프롬프트에서 사고 토큰 수의 상한을 지정한다.
- (b) Step-conditional control: 각 단계가 약 100개의 토큰으로 구성된다고 가정하고, 생각하는 단계 수의 상한을 지정한다.
- (c) Class-conditional control: 모델에게 짧은 시간 또는 긴 시간 동안 생각하도록 지시하는 두 개의 프롬프트를 사용한다.
- Rejection sampling: 생성된 결과가 사전 정의된 계산 예산을 충족할 때까지 샘플링을 반복한다. 이 오라클 방식은 응답의 길이에 따른 사후 확률 분포를 포착한다.
2. Metrics
저자들은 test-time scaling을 여러 방법에 걸쳐 측정하기 위한 metric들을 제안하였다. 중요한 점은 방법이 달성할 수 있는 정확도뿐만 아니라 제어 가능성과 test-time scaling 기울기도 고려한다는 것이다. 고려하는 각 방법에 대해, 고정된 벤치마크에서 test-time 계산량을 변경하여 평가 세트 $a \in \mathcal{A}$를 실행한다. 이렇게 하면 계산량을 x축으로 하고 정확도를 y축으로 하는 piece-wise linear function $f$가 생성된다.
저자들은 세 가지 metric을 측정하였다.
\[\begin{equation} \textrm{Control} = \frac{1}{\vert \mathcal{A} \vert} \sum_{a \in \mathcal{A}} \unicode{x1D7D9} (a_\textrm{min} \le a \le a_\textrm{max}) \end{equation}\]여기서 \(a_\textrm{min}\), \(a_\textrm{max}\)는 미리 지정된 최소/최대 test-time 컴퓨팅 양을 나타낸다. 본 논문의 경우 토큰 수이며, 저자들은 \(a_\textrm{max}\)만 제한하였다. 생성된 토큰은 test-time 컴퓨팅에 사용된 양에 해당하므로, 이 metric은 방법이 test-time 컴퓨팅 사용에 대한 제어 가능성을 허용하는 정도를 측정한다.
\[\begin{equation} \textrm{Scaling} = \frac{1}{\binom{\vert \mathcal{A} \vert}{2}} \sum_{\substack{a, b \in \mathcal{A} \\ b > a}} \frac{f(b) - f(a)}{b - a} \end{equation}\]Scaling은 piece-wise linear function $f$의 평균 기울기이다. 유용한 방법은 Scaling이 양수여야 하며 클수록 좋다.
\[\begin{equation} \textrm{Performance} = \max_{a \in \mathcal{A}} f(a) \end{equation}\]Performance는 단순히 벤치마크에서 해당 방법이 달성하는 최대 성능이다. 단조롭게 증가하는 scaling을 가진 방법은 이론적으로 어떤 벤치마크에서도 궁극적으로 100% 성능을 달성할 수 있다. 그러나 저자들이 조사하는 방법들은 결국 성능이 평탄해지거나, 제어 또는 context window 제한으로 인해 추가적인 scaling에 실패하였다.
Experiments
1. Results
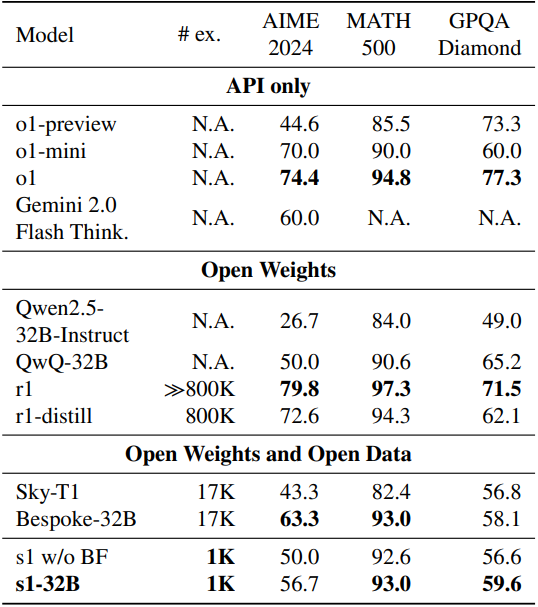
다음은 s1-32B를 다른 모델들과 비교한 결과이다. (# ex.는 fine-tuning에 사용된 예제 수, BF는 budget forcing)
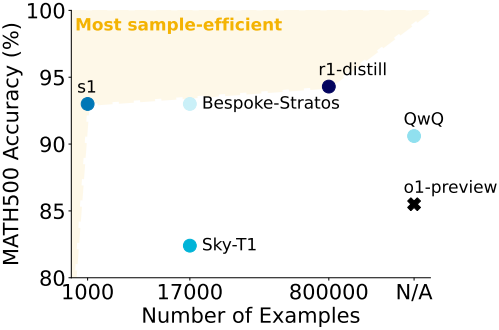
다음은 (a) budget forcing을 통한 sequential scaling과 (b) 다수결 투표를 통한 parallel scaling을 비교한 그래프이다.

2. Ablations
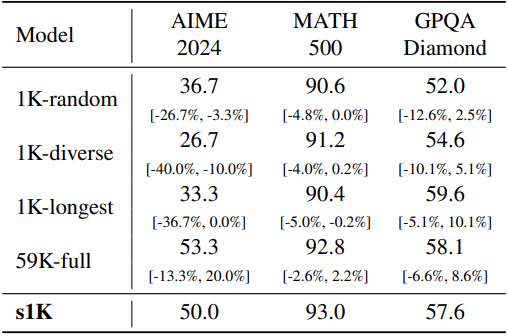
다음은 s1K 데이터에 대한 ablation 결과이다.
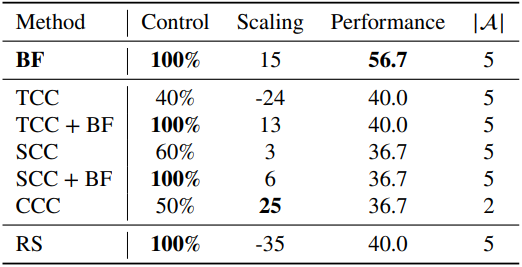
다음은 AIME24에서의 test-time scaling 방법에 대한 ablation 결과이다. ($\vert \mathcal{A} \vert$는 각 metric을 평가하기 위한 실행 횟수, BF는 budget forcing, TCC/SCC/CCC는 token/step/class-conditional control, RS는 rejection sampling)
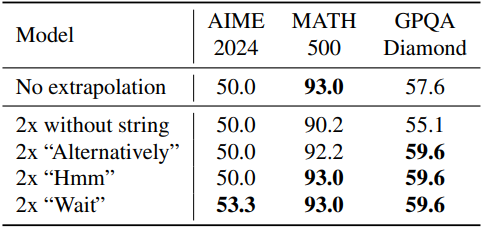
다음은 사고 시간을 늘리기 위한 문자열에 대한 ablation 결과이다. (end-of-thinking 토큰을 두 번 무시하고 문자열을 추가)
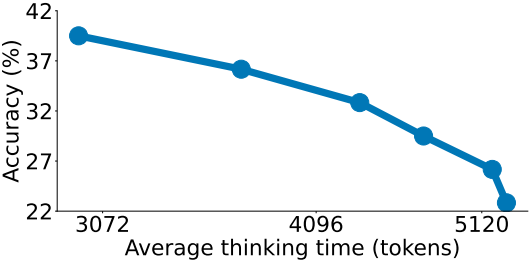
다음은 모든 생성이 3500, 4000, 5000, 8000, 16000개 미만의 사고 토큰을 가질 때까지 rejection sampling하였을 때의 결과이며, 샘플당 평균 655, 97, 8, 3, 2, 1번의 시도가 필요하다.
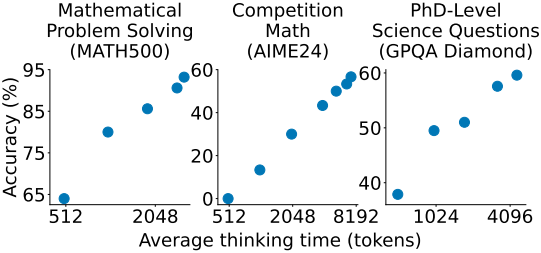
3. Discussion
다음은 sequential scaling과 parallel scaling을 동시에 사용하였을 때의 결과이다. Sequential scaling의 경우, 모델이 최대 32, 64, 256, 512단계를 사용하도록 프롬프팅 하였다. REBASE와 다수결 투표의 경우, 집계할 16개의 병렬 궤적을 생성하였다.