[논문리뷰] rStar-Math: Small LLMs Can Master Math Reasoning with Self-Evolved Deep Thinking

ICML 2025. [Paper] [Github]
Xinyu Guan, Li Lyna Zhang, Yifei Liu, Ning Shang, Youran Sun, Yi Zhu, Fan Yang, Mao Yang
Microsoft Research Asia
8 Jun 2025

Introduction

본 논문에서는 SOTA 수학적 추론 성능을 달성한 자가 진화형 시스템 2 스타일 추론 접근법인 rStar-Math를 소개한다. rStar-Math는 7B 모델 크기로도 까다로운 수학 대회 벤치마크에서 OpenAI o1과 동등하거나 심지어 능가했다. 데이터 합성을 위해 LLM에 의존하는 기존 방법들과 달리, rStar-Math는 Monte Carlo Tree Search (MCTS)와 함께 소규모 언어 모델(SLM)을 활용하여 자가 진화 프로세스를 구축하고, 반복적으로 고품질 학습 데이터를 생성한다. 자가 진화를 위해 rStar-Math는 세 가지 핵심 혁신을 도입하였다.

첫째, 새로운 Code-augmented CoT 데이터 합성 방법으로, 광범위한 MCTS rollout을 수행하여 MCTS Q-value를 갖는 step-by-step으로 검증된 추론 궤적을 생성한다. 구체적으로, 수학 문제 해결은 MCTS 내에서 여러 step의 생성으로 분해된다. 각 step에서 policy 모델 역할을 하는 SLM은 후보 노드를 샘플링하며, 각 노드는 one-step CoT와 해당 Python 코드를 생성한다. 생성 품질을 검증하기 위해 Python 코드 실행이 성공한 노드만 유지하여 중간 step의 오류를 완화한다. 또한, 광범위한 MCTS rollout은 각 중간 step의 기여도에 따라 Q-value를 자동으로 할당한다. 정답으로 이어지는 더 많은 궤적에 기여하는 step은 더 높은 Q-value를 부여받고 더 높은 품질로 간주된다. 이를 통해 SLM이 생성하는 추론 궤적이 정확하고 고품질의 중간 step으로 구성되도록 보장한다.

둘째, process preference model (PPM) 역할을 하는 SLM을 학습시켜 reward 모델을 구현하였으며, 이를 통해 각 수학 추론 단계에 대한 reward 레이블을 안정적으로 예측한다. PPM은 광범위한 MCTS rollout을 사용했음에도 불구하고 Q-value가 각 추론 step을 평가하기에 충분히 정확하지는 않지만, Q-value가 좋은 step과 좋지 못한 step을 안정적으로 구분할 수 있다는 사실을 활용한다. 따라서 이 학습 방법은 Q-value를 기반으로 각 step에 대한 선호도 쌍을 구성하고 pairwise ranking loss를 사용하여 각 추론 step에 대한 PPM의 점수 예측을 최적화한다.

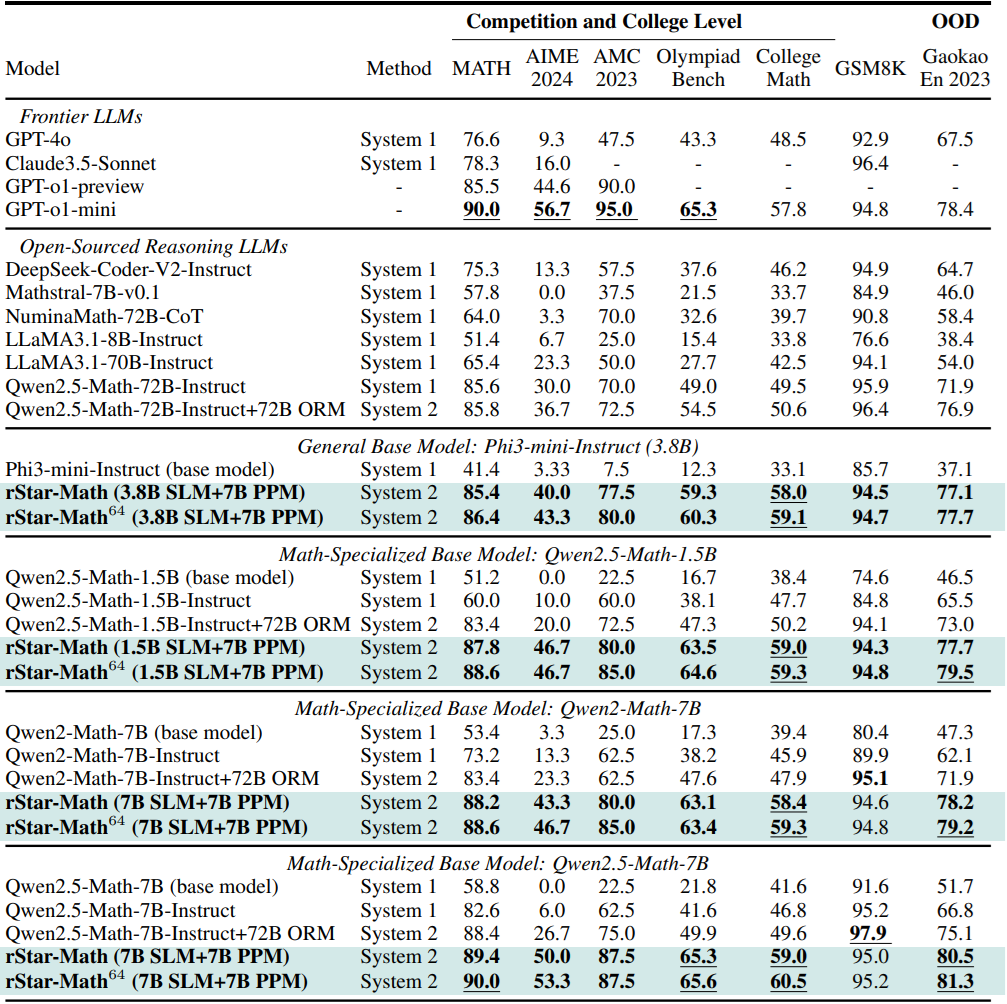
마지막으로, 저자들은 policy 모델과 PPM을 처음부터 점진적으로 구축하는 4라운드 자가 진화 레시피를 제안하였다. 먼저 공개적으로 이용 가능한 소스에서 74.7만 개의 수학 문제 데이터셋을 큐레이팅하였다. 각 라운드에서 최신 policy 모델과 PPM을 사용하여 MCTS를 수행하고, 위의 두 가지 방법을 사용하여 다음 라운드를 위한 더욱 고품질의 학습 데이터를 생성한다. 각 라운드의 policy 모델, PPM, 추론 궤적, 학습 데이터 커버리지가 모두 점점 향상된다.

8개의 궤적을 사용하는 MATH 벤치마크에서 rStar-Math는 Qwen2.5-Math-7B의 성능을 58.8%에서 89.4%로, Qwen2.5-Math-1.5B의 성능을 51.2%에서 87.8%로 향상시켰다. 64개의 궤적을 사용하는 경우, 점수는 각각 90%와 88.4%로 상승하여 o1-preview보다 각각 4.5%와 2.6% 높은 성능을 보이며 o1-mini의 90%와 비슷한 성능을 보였다. 올림피아드급 AIME 2024에서 rStar-Math는 평균 53.3%를 풀었으며, 이는 o1-preview를 포함한 모든 오픈소스 LLM보다 8.7% 더 높은 수치이다.

Methodology

본 논문에서는 두 개의 7B SLM을 사용하여 더 높은 품질의 학습 데이터를 생성하는 방법을 탐구하였다. 그러나 자가 생성 데이터는 SLM에 심각한 문제를 야기한다. SLM은 종종 정답을 생성하지 못하고, 최종 정답이 맞더라도 중간 step에 오류가 있거나 품질이 좋지 않은 경우가 많다. 더욱이 SLM은 GPT-4와 같은 고급 모델에 비해 더 적은 수의 문제를 해결한다.

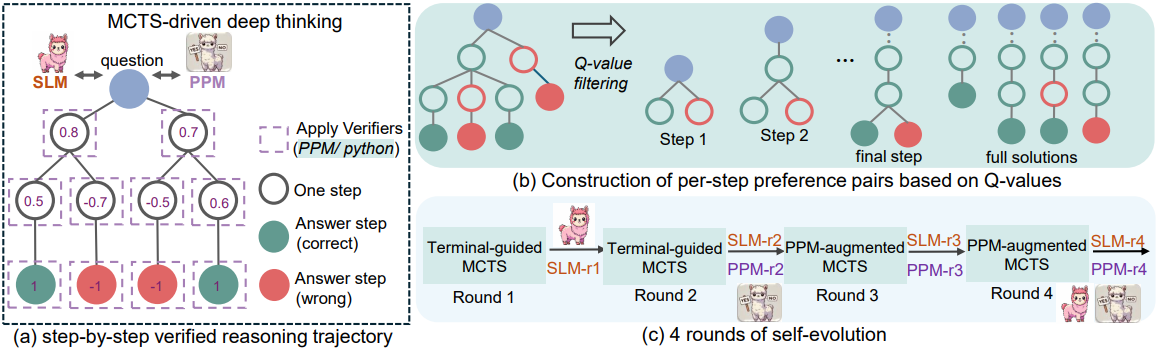
저자들은 오류와 저품질의 중간 step을 완화하기 위해, code-augmented CoT 합성 기법을 도입하였다. 이 기법은 광범위한 MCTS rollout을 수행하여 Q-value가 주석으로 달린 step-by-step으로 검증된 추론 궤적을 생성한다. 또한, 어려운 문제에 대한 SLM 성능을 더욱 향상시키기 위해 총 4라운드의 자가 진화 레시피를 도입하였다. 각 라운드에서 policy SLM과 process preference model (PPM) 모두 더 강력한 버전으로 업데이트되어, 더 어려운 문제를 점진적으로 해결하고 더 높은 품질의 학습 데이터를 생성한다.

1. Step-by-Step Verified Reasoning Trajectory

문제 $x$와 policy 모델 $M$이 주어졌을 때, 표준 MCTS를 사용하여 step-by-step 해답 탐색을 위한 탐색 트리를 점진적으로 구성한다. 루트 노드는 질문 $x$를 나타내고, 자식 노드는 $M$이 생성한 중간 step $s$에 해당한다. 터미널 노드 $s_d$에서 끝나는 루트-리프 경로는 $\textbf{t} = x \oplus s_1 \oplus \ldots \oplus s_d$의 궤적을 형성하며, 각 step $s_i$에 Q-value $Q(s_i)$가 할당된다. 탐색 트리 $\mathcal{T}$에서 궤적 \(\mathbb{T} = \{\textbf{t}^1, \ldots, \textbf{t}^n\}\)을 추출한다.

목표는 $\mathcal{T}$에서 고품질 궤적을 선택하여 학습 세트를 구성하는 것이다. 이를 위해 code-augmented CoT 합성 방법을 도입하여 품질이 낮은 생성을 필터링하고 광범위한 rollout을 수행하여 Q-value 정확도의 신뢰성을 개선한다.

Code-augmented CoT Generation

기존 MCTS 접근법은 주로 자연어(NL) CoT를 생성하였다. 그러나 LLM은 종종 hallucination에 시달려 잘못되거나 관련 없는 step을 생성하면서도 우연히 정답에 도달하는 경우가 많다. 이러한 결함 있는 step은 감지하고 제거하기가 어렵다. 이를 해결하기 위해 본 논문에서는 code-augmented CoT를 제안하였다. Policy 모델은 해당 Python 코드와 함께 one-step 자연어 CoT를 생성하며, 자연어 CoT는 Python 주석으로 포함된다. Python 코드가 성공적으로 실행된 생성만 유효한 후보로 유지된다.

구체적으로 루트 노드 $x$에서 시작하여 selection, expansion, simulation, back-propagation을 통해 여러 MCTS iteration을 수행한다. Step $i$에서 최신 추론 궤적 $x \oplus s1 \oplus \ldots \oplus s_{i-1}$을 현재 state로 수집한다. 이 state를 기반으로 policy 모델이 $n$개의 후보 $s_{i,0}, \ldots, s_{i,n-1}$을 생성한다. 그런 다음, Python 코드를 실행하여 유효한 노드를 필터링한다. 각 생성 $s_{i,j}$는 이전 모든 step의 코드와 연결되어 $s_1 \oplus \ldots \oplus s_{i-1} \oplus s_{i,j}$를 형성한다. 성공적으로 실행된 후보는 유효한 노드로 유지되고 PPM에서 점수를 매겨 Q-value $q(s_i)$를 할당한다. 그런 다음, UCT를 사용하여 $n$개의 후보 노드 중 최적의 노드를 선택한다.

\[\begin{equation} \mathrm{UCT}(s) = Q(s) + c \sqrt{\frac{\ln N_\textrm{parent} (s)}{N (s)}}, \quad \textrm{where} \; Q(s) = \frac{q(s)}{N(s)} \end{equation}\]

($N(s)$는 노드 $s$의 방문 횟수, $N_\textrm{parent}(s)$는 $s$의 부모 노드의 방문 횟수)

최종 답에 도달하거나 최대 트리 깊이에 도달하여 최종 노드에 도달할 때까지 이 과정을 반복한다. 이를 rollout이라고 한다. Rollout이 정답에 도달했는지 여부에 따라 back-propagation을 수행하여 궤적의 Q-value 점수를 업데이트한다.

Extensive Rollouts for Q-value Annotation

위 식에서 정확한 Q-value $Q(s)$는 MCTS가 올바른 문제 해결 경로를 안내하고 궤적 내에서 고품질 step을 식별하는 데 필수적이다. AlphaGo와 rStar를 따라, MCTS rollout을 수행하여 각 step에 Q-value를 할당한다. 그러나 rollout이 충분하지 않으면 최적이 아닌 step을 과대평가하는 등 잘못된 Q-value 할당이 발생할 수 있다.

이 문제를 완화하기 위해, 각 rollout 내에서 최종 정답 달성에 대한 각 step의 기여도를 기반으로 Q-value를 업데이트한다. 광범위한 MCTS rollout을 통해 지속적으로 정답으로 이어지는 step은 더 높은 Q-value를 얻고, 간헐적으로 성공하면 적당한 Q-value를 얻고, 지속적으로 잘못된 step은 낮은 Q-value를 얻는다.

본 논문은 이러한 step-level Q-value를 얻기 위해 두 가지 annotation 방법을 도입하였다.

Terminal-guided annotation

처음 두 라운드 동안 PPM을 사용할 수 없거나 정확도가 부족할 경우, terminal-guided annotation을 사용한다. \(q(s_i)^k\)를 $k$번째 rollout에서 back-propagation 후 step $s_i$에 대한 $q$ 값이라 하면, step별 Q-value를 다음과 같이 계산한다.

\[\begin{equation} q(s_i)^k = q(s_i)^{k-1} + q(s_d)^k \end{equation}\]

첫 번째 rollout에서 초기 $q$ 값은 $q(s_i)^0 = 0$이다. 이 step에서 정답이 자주 나오면 $q$ 값이 증가하고, 그렇지 않으면 감소한다. 최종 노드 $s_d$는 정답일 경우 $q(s_d) = 1$, 그렇지 않을 경우 $q(s_d) = −1$로 평가된다.

PPM-augmented annotation

세 번째 라운드부터는 PPM을 사용하여 각 step에 점수를 매겨 더욱 효과적인 생성을 수행한다. 유의미한 $q$ 값을 얻기 위해 여러 번의 rollout을 필요로 하는 terminal-guided annotation 방식과 달리, PPM은 0이 아닌 초기 $q$ 값을 직접 예측한다. 또한 PPM은 policy 모델이 더 높은 품질의 step을 생성하도록 지원하여 올바른 경로로 해답을 가이드한다.

Step $s_i$에 대해 PPM은 부분 궤적을 기반으로 $q(s_i)^0$ 값을 예측한다.

\[\begin{equation} q(s_i)^0 = \textrm{PPM} (x \oplus s_1 \oplus s_2 \oplus \ldots \oplus s_{i-1} \oplus s_i) \end{equation}\]

이 $q$ 값은 MCTS back-propagation을 통해 터미널 노드의 $q(s_d)$ 값을 기반으로 업데이트된다. 터미널 노드 $s_d$의 경우, 학습 데이터 생성 시 PPM 점수를 사용하지 않는다. 대신, 실제 레이블을 기반으로 더 정확한 점수를 할당한다.

2. Process Preference Model

고품질의 step 수준 학습 데이터를 확보하는 것은 여전히 어렵다. 기존 방법은 사람이 직접 작성한 주석이나 MCTS에서 생성한 점수를 사용하여 각 step의 점수를 레이블링하였다. 이렇게 레이블링된 점수는 학습 타겟으로 사용되며, MSE loss와 같은 방법을 사용하여 예측 점수와 레이블링된 점수의 차이를 최소화한다. 결과적으로, 레이블링된 step 수준 점수의 정확도가 최종 reward 모델의 효과를 결정한다.

그러나, 정확한 step별 점수를 매기는 것은 여전히 해결되지 않았다. 광범위한 MCTS 도입을 통해 Q-value의 신뢰성은 향상되었지만, 세분화된 step별 품질을 정확하게 평가하는 것은 여전히 어렵다. 전문가 수준의 인간 주석조차도 일관성, 특히 대규모 환경에서 어려움을 겪으며, 이로 인해 학습 레이블에 내재된 노이즈가 발생한다.

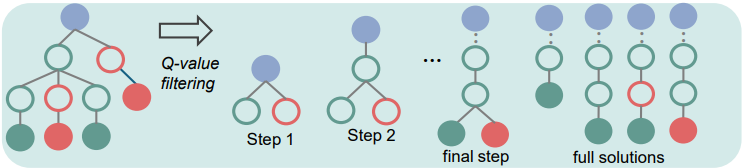
본 논문은 step 수준의 positive-negative 선호도 쌍을 구성하여 process preference model (PPM)을 학습시키는 새로운 학습 방법을 도입하였다. Q-value를 직접적인 reward 레이블로 사용하는 대신, 선호도 쌍 구성을 위해 MCTS 트리에서 step을 선택하는 데 Q-value를 사용한다. 각 step에서 Q-value가 가장 높은 두 후보를 positive step으로, Q-value가 가장 낮은 두 후보를 negative step으로 선택한다.

중요한 점은 선택된 positive step은 정답으로, negative step은 오답으로 이어져야 한다는 것이다. 중간 step에서는 positive 쌍과 negative 쌍이 동일한 이전 step을 공유한다. 단, 최종 답변 step의 경우, 동일한 추론 경로가 다른 최종 답변을 생성하는 경우가 드물기 때문에 이러한 제약을 완화한다. 평균 Q-value가 가장 높은 두 개의 정답 경로를 positive로, 평균 Q-value가 가장 낮은 두 개의 오답 경로를 negative로 선택한다.

다음과 같이, 표준 Bradley-Terry 모델을 사용하여 pairwise rank loss를 정의한다.

\[\begin{equation} \mathcal{L}_\textrm{ppm} (\theta) = -\frac{1}{4} \mathbb{E}_{x, y_i^\textrm{pos}, y_i^\textrm{neg} \in \mathbb{D}} [\log (\sigma (r_\theta (x, y_i^\textrm{pos}) - r_\theta (x, y_i^\textrm{neg})))] \\ \textrm{when } i \textrm{ is not final answer step}, \; \begin{cases} y_i^\textrm{pos} = s_1 \oplus \ldots \oplus s_{i-1} \oplus s_i^\textrm{pos} \\ y_i^\textrm{neg} = s_1 \oplus \ldots \oplus s_{i-1} \oplus s_i^\textrm{neg} \end{cases} \end{equation}\]

(\(r_\theta (x, y_i)\)는 PPM 출력, $x$는 문제, $y$는 첫 번째 step에서 $i$번째 step으로 가는 궤적, $\sigma$는 sigmoid function)

3. Self-Evolved Deep Thinking

Math Problems Collection

저자들은 주로 NuminaMath와 MetaMath에서 정답이 있는 74.7만 개의 수학 문제로 구성된 대규모 데이터셋을 수집하였다. 특히, 초등학교 수준의 문제가 LLM의 복잡한 수학 추론 능력을 크게 향상시키지 않는다는 점을 고려하여 NuminaMath의 대회 수준 문제 (ex. 올림피아드, AIME/AMC)만 포함했다. 제한된 대회 수준 문제를 보완하기 위해, 7,500개의 MATH train set과 3,600개의 AMC-AIME train set의 시드 문제를 기반으로 GPT-4를 사용하여 새로운 문제를 합성했다. 그러나 GPT-4는 종종 풀 수 없는 문제나 어려운 시드 문제에 대한 잘못된 해답을 생성했다. 이러한 문제를 필터링하기 위해, GPT-4가 문제당 10개의 해답을 생성하도록 하고, 최소 3개의 일관된 해답을 가진 문제만 유지하도록 했다.

Reasoning Trajectories Collection

747k 수학 데이터셋의 원래 해답을 사용하는 대신, 더 높은 품질의 step-by-step으로 검증된 추론 궤적을 생성하기 위해 광범위한 MCTS rollout을 수행한다. 각 라운드에서 수학 문제당 16번의 rollout을 수행하여 16개의 추론 궤적을 생성한다. 생성된 궤적의 정답 비율을 기준으로 문제를 난이도별로 분류한다.

• 쉬움: 모든 해답이 맞은 문제
• 보통: 맞은 해답도 있고 틀린 해답도 있는 문제
• 어려움: 모든 해답이 틀린 문제

정답 궤적이 없는 어려움 문제의 경우, 16번의 rollout을 포함하는 추가 MCTS를 수행한다. 그 후, 모든 step-by-step 궤적과 Q-value를 수집하고 필터링하여 policy SLM과 PPM을 학습시킨다.

Self-evolution Recipe

SLM의 성능이 약하기 때문에, 더 높은 품질의 데이터를 점진적으로 생성하기 위해 총 4라운드의 자가 진화를 수행한다. 각 라운드는 MCTS를 사용하여 step-by-step으로 검증된 추론 궤적을 생성하고, 이를 사용하여 새로운 policy SLM과 PPM을 학습시킨다. 이렇게 생성된 새로운 모델은 다음 라운드에서 사용된다.

Round 1: Bootstrapping an initial strong policy SLM-r1

SLM이 상당히 좋은 학습 데이터를 스스로 생성할 수 있도록, 초기 강력한 policy 모델을 fine-tuning하기 위한 부트스트랩 라운드를 수행한다. DeepSeek-Coder-V2-Instruct(236B)를 사용하여 MCTS를 실행하여 supervised fine-tuning (SFT) 데이터를 수집한다. 이 라운드에서는 사용 가능한 reward 모델이 없으므로, Q-value에 대해 terminal-guided annotation을 사용하고 효율성을 위해 MCTS rollout 횟수를 8회로 제한한다. 정답을 도출하기 위해, 평균 Q-value가 가장 높은 상위 2개 궤적을 SFT 데이터로 선택하고, 이를 사용하여 첫 번째 policy SLM인 SLM-r1을 fine-tuning한다.

Round 2: Training a reliable PPM-r2

2라운드에서는 policy 모델을 7B SLM-r1로 업데이트하여 더욱 신뢰할 수 있는 Q-value 주석을 위한 광범위한 MCTS rollout을 수행하고, 최초의 신뢰할 수 있는 reward 모델인 PPM-r2를 학습시킨다. 구체적으로, 문제당 16회의 MCTS rollout을 수행한다. Step-by-step으로 검증된 추론 경로는 품질과 Q-value 정밀도가 모두 상당히 향상된다.

Round 3: PPM-augmented MCTS to significantly improve data quality

3라운드에서는 신뢰할 수 있는 PPM-r2를 사용하여 PPM-augmented MCTS를 수행하여 데이터를 생성하고, 이를 통해 상당히 향상된 품질의 궤적을 도출한다. 생성된 추론 궤적과 Q-value는 새로운 policy SLM-r3와 PPM-r3를 학습시키는 데 사용되며, 두 모델 모두 상당히 개선된다.

Round 4: Solving challenging problems

3라운드 이후, 초등학교 수준의 문제와 MATH 수준의 문제는 높은 성공률을 달성했지만, 올림피아드급 문제의 62.16%만이 training set에 포함되었다. 이는 SLM의 성능 저하 때문만은 아니며, 많은 올림피아드 문제가 GPT-4나 o1로는 해결되지 않은 채 남아 있기 때문이다.

저자들은 데이터 커버리지를 개선하기 위해 간단한 전략을 채택했다. 16번의 rollout 후에도 해결되지 않은 문제에 대해서는 64번의 rollout을 추가로 수행하고, 필요한 경우 128번까지 늘린다. 또한, 다양한 랜덤 시드를 사용하여 여러 차례 MCTS 트리 expansion을 수행한다. 이를 통해 올림피아드급 문제의 성공률을 80.58%로 높였다.

네 번의 자가 진화 라운드를 거친 후, 74.7만 개의 수학 문제 중 90.25%가 training set에 포함되었다. 나머지 미해결 문제 중 대부분은 합성 문제이다. 무작위로 추출한 20개의 문제를 저자들이 직접 검토한 결과, 19개의 문제가 잘못 레이블링되어 있음을 확인했다. 따라서 미해결 문제는 품질이 낮다고 결론짓고 4라운드에서 자가 진화를 중단하였다.

Evaluation

1. Main Results

다음은 여러 수학 벤치마크에서 다른 LLM들과 비교한 결과이다.

다음은 test-time 계산량을 늘렸을 때, 즉 더 많은 궤적을 샘플링하였을 때의 추론 성능을 비교한 그래프이다.

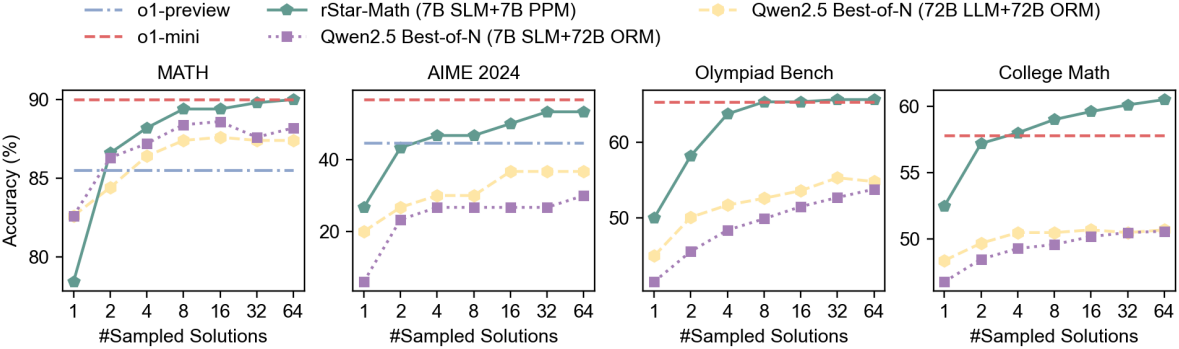
2. Ablation Study and Analysis

다음은 각 라운드가 끝난 후의 모델에 대한 추론 성능을 비교한 결과이다.

다음은 step-by-step으로 검증된 추론 궤적을 SFT 데이터셋으로 사용하였을 때의 추론 성능을 다른 SFT 데이터셋과 비교한 결과이다. (Base model: Qwen2.5-Math-7B)

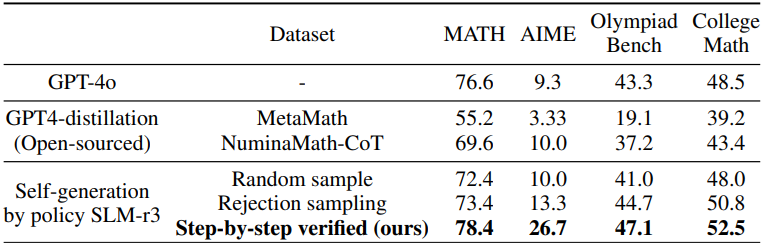
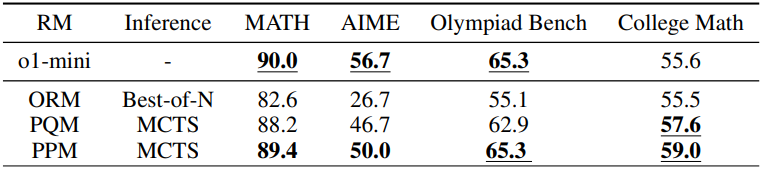
다음은 reward 모델에 대한 ablation 결과이다.