[논문리뷰] Restructuring Vector Quantization with the Rotation Trick

ICLR 2025. [Paper] [Github]
Christopher Fifty, Ronald G. Junkins, Dennis Duan, Aniketh Iyengar, Jerry W. Liu, Ehsan Amid, Sebastian Thrun, Christopher Ré
Stanford University | Google DeepMind
8 Oct 2024

Introduction

Vector quantization (VQ)은 VQ-VAE에서 널리 사용된다. VQ-VAE는 인코더의 출력과 디코더의 입력 사이에 VQ layer가 있는 오토인코더로, bottleneck에서 학습된 표현을 quantize한다. VQ-VAE는 SOTA 생성 모델에서 널리 사용되지만, 그 gradient는 미분 불가능한 VQ layer를 통과해야 하기 때문에 디코더에서 인코더로 바로 흐를 수 없다.

미분 불가능 문제에 대한 해결책은 straight-through estimator (STE)를 통해 기울기를 근사하는 것이다. Backpropagation을 하는 동안 STE는 디코더 입력의 기울기를 인코더 출력으로 복사 붙여넣기 하여 quantization 연산을 완전히 건너뛴다. 그러나 이러한 근사화는 모델 성능의 저하와 codebook collapse로 이어질 수 있다. Codebook collapse는 codebook의 상당 부분이 0으로 수렴하고 모델에서 사용되지 않는 현상이다. Codebook collapse가 발생하지 않더라도 codebook이 종종 활용되지 않아 VQ-VAE의 정보 용량이 제한된다.

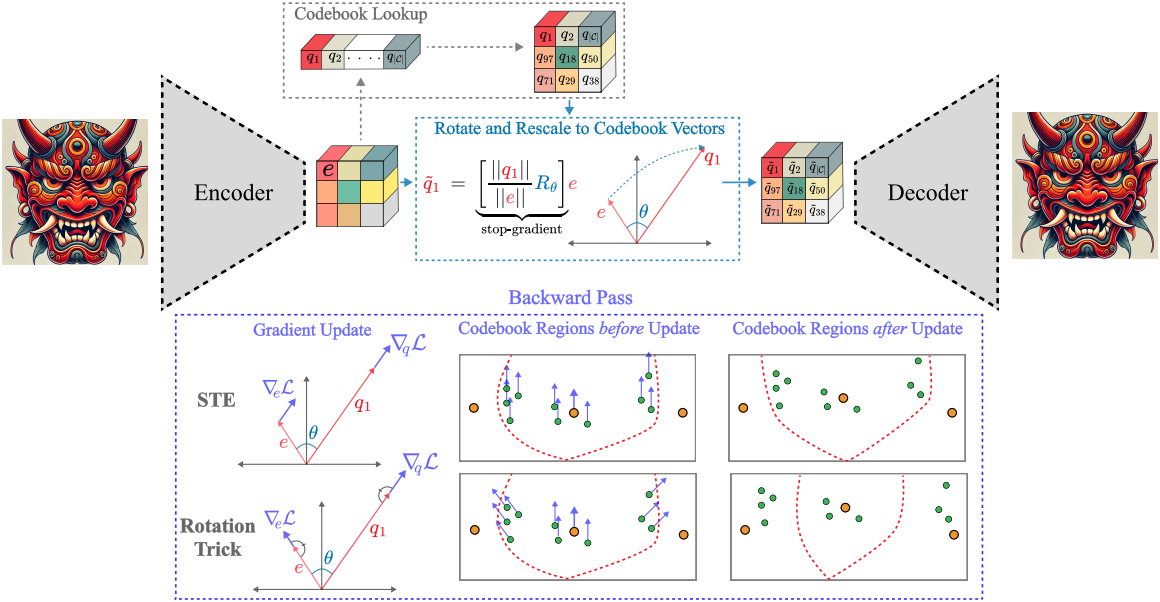
본 논문에서는 VQ-VAE에서 VQ layer를 통해 gradient를 전파하는 대체 방법을 제안하였다. 주어진 인코더 출력 $e$와 가장 가까운 codebook 벡터 $q$에 대해 선형 변환 (rotation, rescaling)을 통해 $e$를 $q$로 부드럽게 변환한 다음 이 $\hat{q}$를 디코더로 보낸다. 디코더의 입력 $\hat{q}$가 이제 $e$의 부드러운 선형 변환으로 처리되므로 디코더에서 인코더로 gradient가 다시 흐른다. Rotation과 rescaling을 통한 미분을 피하기 위해 둘 다 $e$와 $q$에 대한 상수로 처리한다. 이 재구성을 rotation trick이라고 한다.

Rotation trick은 forward pass에서 VQ-VAE의 출력을 변경하지 않는다. 그러나 backward pass 중에 VQ layer 이후의 $q$와 \(\nabla_q \mathcal{L}\) 사이의 각도가 VQ layer 이전의 $e$와 \(\nabla_e \mathcal{L}\) 사이의 각도와 같아진다. 이 각도를 유지하면 상대적 각도 거리와 크기가 gradient로 인코딩되고 동일한 codebook 영역 내의 포인트가 업데이트되는 방식이 변경된다.

STE는 동일한 codebook 영역 내의 모든 포인트에 동일한 업데이트를 적용하여 상대적 거리를 유지한다. 그러나 rotation trick은 gradient 벡터의 방향에 따라 동일한 codebook 영역 내의 포인트를 더 멀리 밀어내거나 더 가깝게 끌어당길 수 있다. 멀리 밀어내는 것은 codebook 사용량 증가에 해당할 수 있고 가깝게 끌어당기는 것은 quantization error를 낮추는 데 해당할 수 있다. 두 경우 모두 왜곡을 줄이고 VQ layer의 정보 용량을 늘리는 데 바람직하다.

Rotation trick은 재구성 성능을 크게 개선하고, codebook 사용량을 늘리고, 인코더 출력과 해당 codebook 벡터 간의 거리를 줄인다. VQGAN을 ImageNet에서 rotation trick으로 학습시키면 재구성 FID가 5.0에서 1.1로, 재구성 IS가 141.5에서 200.2로 개선되고, codebook 사용량이 2%에서 27%로 증가하고, quantization error가 100배 이상 감소한다.

Straight Through Estimator (STE)

입력 $x \in \mathcal{X}$에 대해, 사후 분포 \(p_\mathcal{E} (e \vert x)\)를 parameterize하는 deterministic mapping으로 인코더를 정의한다. VQ layer $\mathcal{Q} (\cdot)$는 인코더 출력 $e$에 가장 가까운 codebook 벡터 $q \in \mathcal{C}$를 선택하는 함수이다.

\[\begin{equation} \mathcal{Q} (q = i \vert e) = \begin{cases} 1 & \; \textrm{if} \; i = \underset{1 \le j \le \vert \mathcal{C} \vert}{\arg \min} \| e - q_j \|_2 \\ 0 & \; \textrm{otherwise} \end{cases} \end{equation}\]

디코더는 재구성에 대한 조건부 분포 \(p_\mathcal{D} (\tilde{x} \vert q)\)를 parameterize하는 deterministic mapping으로 정의된다. VAE에서와 같이 loss function은 ELBO에서 따르며, \(p_\mathcal{E} (e \vert x)\)가 deterministic하고 codebook 벡터에 대한 활용이 균일하다고 가정하기 때문에 KL-divergence 항은 0이 된다.

VQ-VAE에서는 codebook 벡터를 학습하기 위해 codebook loss 항 \(\| \textrm{sg} (e) - q \|_2^2\)를 추가하고 인코더의 출력을 codebook 벡터 쪽으로 끌어오기 위해 commitment loss 항 \(\beta \| e - \textrm{sg} (q) \|_2^2\)를 추가하였다 ($\textrm{sg}$는 stop-gradient). 따라서 예측된 재구성 $\hat{x}$에 대한 전체 loss는 다음과 같다.

\[\begin{equation} \mathcal{L} (\tilde{x}) = \| x - \tilde{x} \|_2^2 + \| \textrm{sg} (e) - q \|_2^2 + \beta \| e - \textrm{sg} (q) \|_2^2 \end{equation}\]

\(\| x - \tilde{x} \|_2^2\) 항만 디코더의 함수이기 때문에 이 항에만 초점을 맞추자. Backpropagation을 하는 동안 모델은 VQ layer 함수 Q(·)를 통해 미분해야 합니다. Backward pass를 세 항으로 나눌 수 있다.

\[\begin{equation} \frac{\partial \mathcal{L}}{\partial x} = \frac{\partial \mathcal{L}}{\partial q} \frac{\partial q}{\partial e} \frac{\partial e}{\partial x} \end{equation}\]

($\frac{\partial \mathcal{L}}{\partial q}$, $\frac{\partial q}{\partial e}$, $\frac{\partial e}{\partial x}$는 각각 디코더, vector quantization layer, 인코더를 통한 backpropagation)

VQ는 미분 불가능하므로 $\frac{\partial q}{\partial e}$를 계산할 수 없고, 이 항을 통해 gradient를 흐르게 하여 backpropagation을 통해 인코더를 업데이트할 수 없다.

미분 불가능성 문제를 해결하기 위해 STE는 $q$에서 $e$로 기울기를 복사한다. 즉, STE는 backward pass에서 $\frac{\partial q}{\partial e}$를 단위 행렬 $I$로 설정한다.

\[\begin{equation} \frac{\partial \mathcal{L}}{\partial x} = \frac{\partial \mathcal{L}}{\partial q} I \frac{\partial e}{\partial x} \end{equation}\]

처음 두 항 $\frac{\partial \mathcal{L}}{\partial q} \frac{\partial q}{\partial e}$는 $\frac{\partial \mathcal{L}}{\partial e}$로 결합되는데, 실제로는 $e$에 의존하지 않는다. 결과적으로 codebook 벡터 $q$에 의해 생성된 Voronoi 파티션 내의 $e$의 위치는 $q$에 가깝든 멀든 인코더에 대한 gradient 업데이트에 영향을 미치지 않는다.

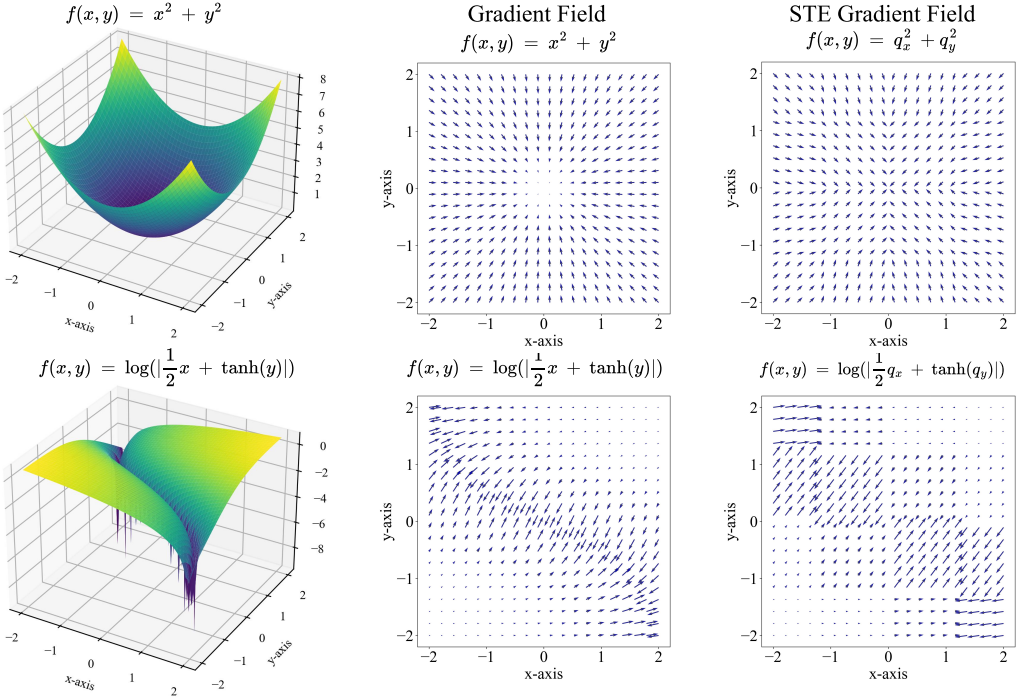
위 그림은 두 가지 예제 함수에 대하여 시각화한 것이다. STE 근사에서 인코더 출력의 gradient는 어디에 인코더 출력 $e$가 있는지와 관계없이 각 Voronoi 파티션의 해당 codebook 벡터의 gradient로 대체된다. 결과적으로 gradient field는 codebook의 16개 벡터에 대해 모두 동일한 gradient 업데이트가 있는 16개의 다른 영역으로 분할된다.

STE를 Hessian 근사나 이중 forward pass로 대체하여 $\frac{\partial \mathcal{L}}{\partial e}$를 계산하면 성능이 더 나빠진다. 이는 $e$에 대한 정확한 gradient를 계산하는 것이 실제로 AutoEncoder의 gradient이며, VAE와 VQ-VAE가 AutoEncoder의 overfitting 경향과 일반화의 어려움을 감안하여 대체하도록 설계된 모델이기 때문이다. 따라서 정확한 gradient를 사용하면 인코더가 AutoEncoder처럼 학습되고 디코더가 VQ-VAE처럼 학습된다. 이러한 불일치는 성능이 떨어지는 또 다른 요인이다.

The Rotation Trick

STE에서 qauntize된 영역 내에서 $e$의 위치는 $q$에 가깝든 멀리 떨어져 있든 인코더에 대한 gradient 업데이트에 영향을 미치지 않으며, 이는 정보를 잃는 것이다. 이 정보를 캡처하는 것, 즉 $q$에 대한 $e$의 위치를 ​​사용하여 gradient를 $\frac{\partial q}{\partial e}$를 통해 변환하는 것은 인코더의 gradient 업데이트에 유익할 수 있으며 STE보다 개선될 수 있다.

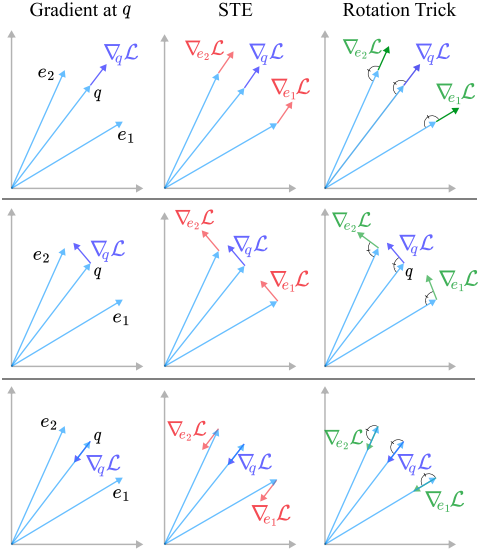
기하학적으로 볼 때, gradient \(\nabla_q \mathcal{L}\)을 $q$에서 $e$로 어떻게 움직일지, 그리고 이 움직임 동안 \(\nabla_q \mathcal{L}\)과 $q$의 어떤 특성을 보존해야 하는지가 중요하다. STE는 gradient를 $q$에서 $e$로 옮겨 방향과 크기가 보존되도록 한다. 그러나 본 논문은 \(\nabla_q \mathcal{L}\)을 $e$로 이동시킬 때 \(\nabla_q \mathcal{L}\)과 $q$ 사이의 각도가 보존되도록 한다. 이 접근 방식을 rotation trick이라 부른다.

1. The Rotation Trick Preserves Angles

인코더 출력 $e$에 대해 $q = \mathcal{Q}(e)$가 해당 codebook 벡터를 나타낸다고 하자. $\mathcal{Q}(\cdot)$는 미분 불가능하므로 backward pass 중에 이 $\mathcal{Q}(\cdot)$를 통해 gradient가 흐를 수 없다. STE는 \(\nabla_q \mathcal{L}\)이 $q$에서 $e$로 이동할 때 기울기 \(\nabla_q \mathcal{L}\)의 방향과 크기를 유지하여 이 문제를 해결하였다.

\[\begin{equation} \tilde{q} = e - \underbrace{(q - e)}_{\textrm{constant}} \end{equation}\]

이는 인코더 출력의 gradient를 디코더 입력의 gradient로 설정한다. Rotation trick은 forward pass를 $q$와 $e$를 정렬하는 rotation 및 rescaling으로 수정한다.

\[\begin{equation} \tilde{q} = \underbrace{\left[ \frac{\| q \|}{\| e \|} R \right]}_{\textrm{constant}} \end{equation}\]

$R$은 $e$를 $q$에 맞추는 회전 변환이고, $\frac{| q |}{| e |}$는 $e$를 $q$와 같은 크기로 rescaling한다. $R$과 $\frac{| q |}{| e |}$는 모두 $e$의 함수이다. 이 종속성을 통한 미분을 피하기 위해 미분할 때 $R$와 $\frac{| q |}{| e |}$를 상수로 취급한다.

Rotation trick은 forward pass의 출력을 변경하지 않지만 backward pass는 변경한다. STE에서처럼 $\frac{\partial q}{\partial e} = I$로 설정하는 대신, rotation trick은 $\frac{\partial q}{\partial e}$를 rotation 및 rescaling 변환으로 설정한다.

\[\begin{equation} \frac{\partial \tilde{q}}{\partial e} = \frac{\| q \|}{\| e \|} R \end{equation}\]

결과적으로 $\frac{\partial q}{\partial e}$는 $q$의 codebook 파티션에서 $e$의 위치에 따라 변경되고, 특히 \(\nabla_q \mathcal{L}\)과 $q$ 사이의 각도는 \(\nabla_q \mathcal{L}\)이 $e$로 이동함에 따라 유지된다. STE가 기울기를 $q$에서 $e$로 변환하지만, rotation trick은 \(\nabla_q \mathcal{L}\)과 $q$ 사이의 각도가 유지되도록 회전한다.

2. Efficient Rotation Computation

$e$를 $q$로 회전시키는 회전 변환 $R$은 Householder matrix reflection을 사용하여 효율적으로 계산할 수 있다.

\[\begin{equation} \hat{e} = \frac{e}{\| e \|}, \; \hat{q} = \frac{q}{\| q \|}, \; \lambda = \frac{\| q \|}{\| e \|}, \; r = \frac{\hat{e} + \hat{q}}{\| \hat{e} + \hat{q} \|} \end{equation}\]

로 정의하면, $e$를 $q$에 맞추는 회전 및 rescaling은 다음과 같다.

\[\begin{aligned} \tilde{q} &= \lambda R e \\ &= \lambda (I - 2rr^\top + 2 \hat{q} \hat{e}^\top) e \\ &= \lambda (e - 2rr^\top e + 2 \hat{q} \hat{e}^\top e) \end{aligned}\]

이런 방식으로 계산하면 외적을 계산하지 않아도 되므로 최소한의 GPU VRAM을 소모한다. 또한 STE로 학습한 VQ-VAE와 rotation trick으로 학습한 VQ-VAE 간의 학습 시간은 거의 동일하다.

3. Voronoi Partition Analysis

VQ는 왜곡(quantization 오차 \(\| e - q \|_2^2\))이 낮고 정보 용량(codebook 활용도)이 높을 때 잘 작동한다. Rotation trick으로 학습한 VQ-VAE는 STE로 학습한 VQ-VAE와 비교했을 때 quantization 오차를 10배 줄이고 codebook 사용을 크게 늘린다.

STE가 동일한 파티션 내의 모든 포인트에 동일한 업데이트를 적용하는 반면, rotation trick은 Voronoi 영역 내의 포인트 위치에 따라 업데이트를 변경한다. Gradient 벡터의 방향에 따라 동일한 영역 내의 포인트를 더 멀리 밀어내거나 더 가깝게 끌어당길 수 있다. 밀어내는 경우 codebook 사용량이 증가되는 경우에 해당하며, 가깝게 끌어당기는 경우 quantization 오차를 낮추는 경우에 해당한다.

($e$와 $q$ 사이 거리의 변화)

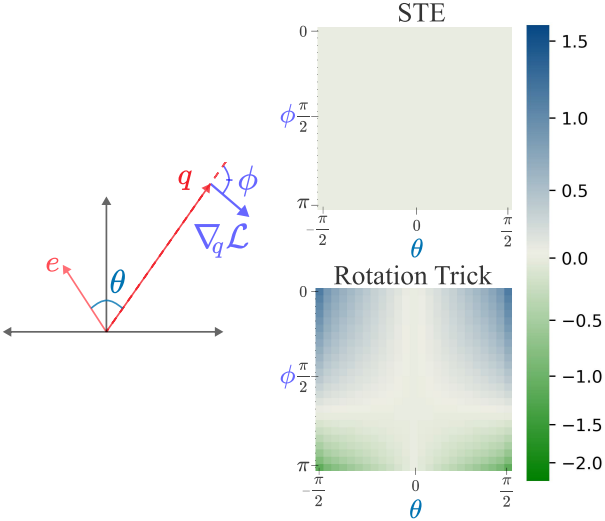
$\theta$를 $e$와 $q$ 사이의 각도로 하고 $\phi$를 $q$와 \(\nabla_q \mathcal{L}\) 사이의 각도라 하자. \(\nabla_q \mathcal{L}\)과 $q$가 같은 방향을 가리킬 때, 즉 $\phi < \pi/2$일 때, $\theta$의 크기가 큰 인코더 출력은 STE 업데이트에 의해 이동될 것보다 더 멀리 밀려난다. 위 그림은 이 효과를 보여준다. $\theta$가 큰 점(파란색 영역)은 $\theta$가 작은 점(상아색 영역)보다 $q$에서 더 멀리 이동한다.

\(\nabla_q \mathcal{L}\)과 $q$가 반대 방향을 가리킬 때, 즉 $\phi > \pi/2$일 때, $\theta$의 크기가 큰 인코더 출력은 업데이트 후 codebook 벡터 쪽으로 더 가깝게 당겨진다.

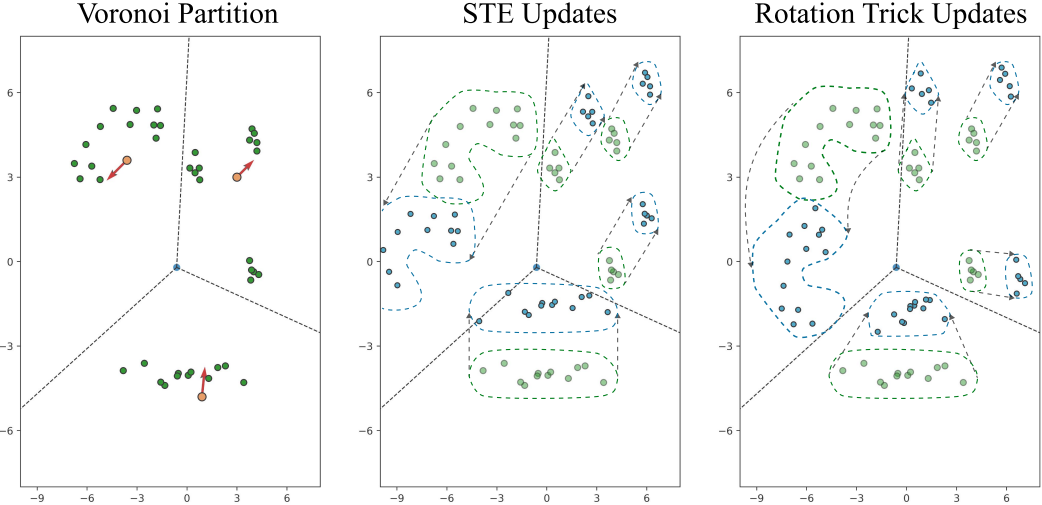
위 그림에서 오른쪽 상단 파티션은 $\phi < \pi/2$에 해당하며, codebook 벡터에 대한 각도가 비교적 큰 경계에 있는 두 개의 클러스터는 밀려나고 codebook 벡터에 대한 각도가 작은 클러스터는 함께 이동한다. 경계에 있는 점을 다른 영역으로 밀어내는 것은 codebook 활용도를 높이는 데 바람직하며, 이 기능은 같은 영역의 모든 점을 같은 양만큼 움직이는 STE에서는 발생하지 않는다.

하단 파티션은 $\phi > \pi/2$에 해당하며, 동일한 Voronoi 영역 내의 점들 사이의 거리는 업데이트된 codebook 벡터의 위치로 끌려감에 따라 감소한다. 점들 사이의 거리를 유지하는 STE 업데이트와 달리, rotation trick은 $\theta$가 큰 점들을 업데이트 후 codebook 벡터 쪽으로 더 가깝게 당긴다. 이 기능은 quantization error를 줄이고 인코더가 타겟 codebook 벡터에서 벗어나지 못하게 하는 데 바람직하다.

두 기능을 함께 사용하면 VQ의 두 가지 요구 사항, 즉 정보 용량 증가와 왜곡 감소를 모두 달성할 수 있다. 선택한 codebook 벡터와의 $\theta$가 큰 인코더 출력은 바깥쪽을 가리키는 gradient에 의해 다른, 아마도 사용되지 않는 codebook 영역으로 밀려나 codebook 활용도가 증가한다. 동시에 중심을 가리키는 gradient는 codebook 벡터 주변에 느슨하게 클러스터링된 점들을 서로 더 가깝게 당겨 선택한 codebook 벡터에서 벗어나기 힘들게 만들고 quantization error를 줄인다.

Experiments

1. VQ-VAE Evaluation

다음은 ImageNet에서 학습된 VQ-VAE에 대한 결과이다.

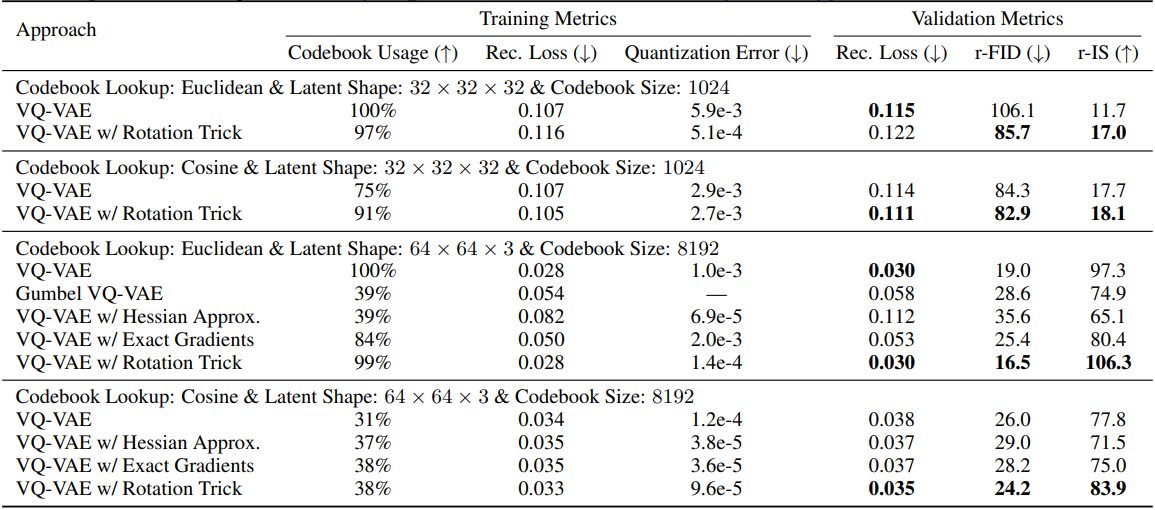
2. VQGAN Evaluation

다음은 autoregressive한 생성을 위한 VQGAN에 대한 결과이다. (ImageNet, FFHQ & CelebA-HQ)

다음은 latent diffusion을 위한 VQGAN에 대한 결과이다. (ImageNet)

3. ViT-VQGAN Evaluation

다음은 ImageNet에서 학습된 ViT-VQGAN에 대한 결과이다.

Limitations

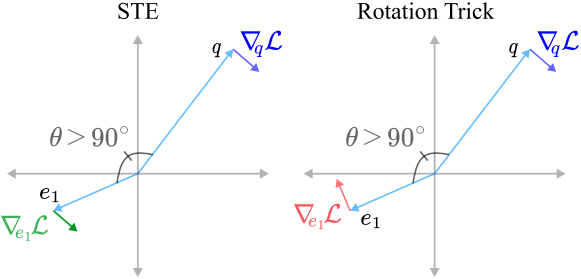
인코더 출력 $e$ 또는 codebook 벡터 $q$가 0 norm에 가까워지면 $e$와 $q$ 사이의 각도가 둔각이 될 수 있다. 이런 경우 rotation trick은 기울기 \(\nabla_q \mathcal{L}\)을 $q$에서 $e$로 전송할 때 과도하게 회전시켜 \(\nabla_q \mathcal{L}\)과 \(\nabla_e \mathcal{L}\)이 다른 방향을 가리키게 된다.

이는 $e \approx q$일 때 \(\nabla_q \mathcal{L} \approx \nabla_e \mathcal{L}\)이라는 가정을 위반하고 STE로 학습시킨 VQ-VAE보다 성능이 떨어질 가능성이 높다. 설계상 codebook 벡터는 매핑된 벡터와 각도가 가까워야 하기 때문에 $e$와 $q$ 사이의 둔각은 매우 가능성이 낮지만, $e$ 또는 $q$가 0 norm을 갖도록 하는 제한이 있는 경우 rotation trick은 STE보다 성능이 떨어질 가능성이 높다.