[논문리뷰] RoFormer: Enhanced Transformer with Rotary Position Embedding
arXiv 2021. [Paper] [HuggingFace]
Jianlin Su, Yu Lu, Shengfeng Pan, Ahmed Murtadha, Bo Wen, Yunfeng Liu
Zhuiyi Technology Co., Ltd.
20 Apr 2021
Introduction
최근 Transfer를 기반으로 구축된 사전 학습된 언어 모델은 다양한 자연어 처리 (NLP) task의 SOTA 성능을 달성했으며, self-attention 메커니즘을 활용하여 주어진 코퍼스의 컨텍스트 표현을 의미적으로 포착한다.
현재 언어 모델들의 self-attention 아키텍처가 위치와 무관하다는 것은 주목할 만한 사실이다. 학습 프로세스에 위치 정보를 인코딩하기 위한 다양한 접근 방식이 제안되었다. 한편으로는 미리 정의된 함수를 통해 생성된 절대적 위치 인코딩이 맥락적 표현에 더해졌고, 다른 한편으로는 상대적 위치 정보를 attention 메커니즘으로 인코딩하는 상대적 위치 인코딩에 초점을 맞췄다.
본 논문은 언어 모델의 학습 프로세스에 위치 정보를 활용하기 위해 Rotary Position Embedding (RoPE)이라는 새로운 방법을 도입하였다. RoPE는 회전 행렬로 절대적 위치를 인코딩하는 한편, self-attention 공식에 명시적인 상대적 위치 종속성을 통합한다. RoPE는 시퀀스 길이 유연성을 가지고 있으며, 상대적 거리가 증가함에 따라 토큰 간 종속성이 감소하며, linear self-attention에 상대적 위치 인코딩을 장착할 수 있다. RoPE를 갖춘 향상된 Transformer인 RoFormer는 다양한 장문 텍스트 분류 벤치마크 데이터셋에서 baseline에 비해 더 나은 성능을 보인다.
Background
$N$개의 입력 토큰의 시퀀스를 \(\mathbb{S}_N = \{w_i\}_{i=1}^N\)이라 하자. \(\mathbb{S}_N\)의 단어 임베딩은 \(\mathbb{E}_N = \{\mathbf{x}_i\}_{i=1}^N\)이며, 여기서 \(\mathbf{x}_i \in \mathbb{R}^d\)는 위치 정보가 없는 토큰 $w_i$의 $d$차원 단어 임베딩 벡터이다.
Self-attention은 먼저 단어 임베딩에 위치 정보를 통합하고 이를 query, key, value 표현으로 변환한다.
\[\begin{aligned} \mathbf{q}_m &= f_q (\mathbf{x}_m, m) \\ \mathbf{k}_n &= f_k (\mathbf{x}_n, n) \\ \mathbf{v}_n &= f_v (\mathbf{x}_n, n) \end{aligned}\]Absolute position embedding
$f_q$, $f_k$, $f_v$의 일반적인 선택은 다음과 같이 absolute position embedding \(\mathbf{p}_i \in \mathbb{R}^d\)를 사용하는 것이다.
\[\begin{aligned} f_q (\mathbf{x}_m, m) &= \mathbf{W}_q (\mathbf{x}_m + \mathbf{p}_m) \\ f_k (\mathbf{x}_n, n) &= \mathbf{W}_k (\mathbf{x}_n + \mathbf{p}_n) \\ f_v (\mathbf{x}_n, n) &= \mathbf{W}_v (\mathbf{x}_n + \mathbf{p}_n) \end{aligned}\]\(\mathbf{p}_i\)는 토큰 \(\mathbf{x}_i\)의 위치에 따라 달라지는 $d$차원 벡터이다. Transformer는 sinusoidal function을 사용하여 \(\mathbf{p}_i\)를 정의하였다.
\[\begin{aligned} \mathbf{p}_{i, 2t} &= \sin (k / 10000^{2t/d}) \\ \mathbf{p}_{i, 2t+1} &= \cos (k / 10000^{2t/d}) \end{aligned}\](\(\mathbf{p}_{i,2t}\)는 $d$차원 벡터 \(\mathbf{p}_i\)의 $2t$번째 요소)
Relative position embedding
Self-Attention with Relative Position Representations 논문은 relative position embedding을 제안하였다.
\[\begin{aligned} f_q (\mathbf{x}_m) &= \mathbf{W}_q \mathbf{x}_m \\ f_k (\mathbf{x}_n, n) &= \mathbf{W}_k (\mathbf{x}_n + \tilde{\mathbf{p}}_r^k) \\ f_v (\mathbf{x}_n, n) &= \mathbf{W}_v (\mathbf{x}_n + \tilde{\mathbf{p}}_r^v) \end{aligned}\]여기서 \(\tilde{\mathbf{p}}_r^k, \tilde{\mathbf{p}}_r^v \in \mathbb{R}^d\)는 학습 가능한 relative position embedding이다. $r = \textrm{clip}(m − n, r_\textrm{min}, r_\textrm{max})$는 위치 $m$과 $n$ 사이의 상대적 거리를 나타낸다. 상대적 위치 정보가 특정 거리를 넘어서면 유용하지 않다는 가설로 상대적 거리를 잘라냈다.
Transformer-XL은 absolute position embedding \(\mathbf{p}_n\)을 relative position embedding \(\tilde{\mathbf{p}}_{m-n}\)로 대체하고, \(\mathbf{p}_m\)을 학습 가능한 벡터 $\mathbf{u}$, $\mathbf{v}$로 대체하였다.
\[\begin{aligned} \mathbf{q}_m^\top \mathbf{k}_n &= \mathbf{x}_m^\top \mathbf{W}_q^\top \mathbf{W}_k \mathbf{x}_n + \mathbf{x}_m^\top \mathbf{W}_q^\top \mathbf{W}_k \mathbf{p}_n + \mathbf{p}_m^\top \mathbf{W}_q^\top \mathbf{W}_k \mathbf{x}_n + \mathbf{p}_m^\top \mathbf{W}_q^\top \mathbf{W}_k \mathbf{p}_n \\ &= \mathbf{x}_m^\top \mathbf{W}_q^\top \mathbf{W}_k \mathbf{x}_n + \mathbf{x}_m^\top \mathbf{W}_q^\top \tilde{\mathbf{W}}_k \tilde{\mathbf{p}}_{m-n} + \mathbf{u}^\top \mathbf{W}_q^\top \mathbf{W}_k \mathbf{x}_n + \mathbf{v}^\top \mathbf{W}_q^\top \tilde{\mathbf{W}}_k \tilde{\mathbf{p}}_{m-n} \end{aligned}\]또한 \(f_v (\mathbf{x}_j) = \mathbf{W}_v \mathbf{x}_j\)로 설정하여 value 항의 위치 정보를 제거하였다. 이후 논문들은 attention 가중치에만 상대적 위치 정보를 인코딩하였다.
Text-to-Text Transfer Transformer (T5)는 학습 가능한 bias $b_{i,j}$를 사용하였으며, 여러 projection matrix들을 사용하여 한 쌍의 단어나 위치를 모델링하였다.
\[\begin{equation} \mathbf{q}_m^\top \mathbf{k}_n = \mathbf{x}_m^\top \mathbf{W}_q^\top \mathbf{W}_k \mathbf{x}_n + \mathbf{p}_m^\top \mathbf{U}_q^\top \mathbf{U}_k \mathbf{p}_n + b_{i,j} \end{equation}\]DeBERTa는 absolute position embedding \(\mathbf{p}_m\)과 \(\mathbf{p}_n\)을 단순히 relative position embedding \(\tilde{\mathbf{p}}_{m-n}\)으로 대체하였다.
\[\begin{equation} \mathbf{q}_m^\top \mathbf{k}_n = \mathbf{x}_m^\top \mathbf{W}_q^\top \mathbf{W}_k \mathbf{x}_n + \mathbf{x}_m^\top \mathbf{W}_q^\top \mathbf{W}_k \tilde{\mathbf{p}}_{m-n} + \tilde{\mathbf{p}}_{m-n}^\top \mathbf{W}_q^\top \mathbf{W}_k \mathbf{x}_n \end{equation}\]이 모든 접근 방식들은 Transformer의 self-attention \(\mathbf{q}_m^\top \mathbf{k}_n\)을 기반으로 변경을 시도하였으며, 일반적으로 컨텍스트 표현에 위치 정보를 직접 추가하도록 도입했다. 반면, 본 논문의 접근 방식은 바로 relative position embedding을 유도하는 것을 목표로 하였다.
Proposed approach
1. Formulation
Transformer 기반 언어 모델링은 일반적으로 self-attention 메커니즘을 통해 개별 토큰의 위치 정보를 활용한다. \(\mathbf{q}_m^\top \mathbf{k}_n\)은 일반적으로 서로 다른 위치에 있는 토큰 간의 지식 전달을 가능하게 한다. 상대적 위치 정보를 통합하기 위해 query \(\mathbf{q}_m\)과 key \(\mathbf{k}_n\)의 내적을 함수 $g$로 공식화해야 한다. 이 함수는 단어 임베딩 \(\mathbf{x}_m\), \(\mathbf{x}_n\)과 이들의 상대적 위치 $m − n$만을 입력 변수로 취한다. 즉, 내적은 상대적인 형태로만 위치 정보를 인코딩해야 한다.
\[\begin{equation} \langle f_q (\mathbf{x}_m, m), f_k (\mathbf{x}_n, n) \rangle = g (\mathbf{x}_m, \mathbf{x}_n, m - n) \end{equation}\]궁극적인 목표는 위의 관계를 준수하기 위해 함수 \(f_q (\mathbf{x}_m, m)\)과 \(f_k (\mathbf{x}_n, n)\)을 풀기 위한 동등한 인코딩 메커니즘을 찾는 것이다.
2. Rotary position embedding
2D case
2차원의 간단한 경우에서는 2D 평면에서의 벡터의 기하학적 속성과 그 복소 형식을 사용하여 해가 다음과 같다.
\[\begin{aligned} f_q (\mathbf{x}_m, m) &= (\mathbf{W}_q \mathbf{x}_m) e^{im \theta} \\ f_k (\mathbf{x}_n, n) &= (\mathbf{W}_k \mathbf{x}_n) e^{in \theta} \\ g (\mathbf{x}_m, \mathbf{x}_n, m-n) &= \textrm{Re} [(\mathbf{W}_q \mathbf{x}_m) (\mathbf{W}_k \mathbf{x}_n)^\ast e^{i(m-n) \theta}] \end{aligned}\]$\textrm{Re} [\cdot]$은 복소수의 실수 부분이고, \((\mathbf{W}_k \mathbf{x}_n)^\ast\)는 \((\mathbf{W}_k \mathbf{x}_n)\)의 켤레 복소수이다. \(f_{\{q,k\}}\)를 다음과 같이 행렬의 곱셈으로 쓸 수 있다.
\[\begin{equation} f_{\{q,k\}} (\mathbf{x}_m, m) = \begin{pmatrix} \cos m \theta & - \sin m \theta \\ \sin m \theta & \cos m \theta \end{pmatrix} \begin{pmatrix} W_{\{q,k\}}^{(11)} & W_{\{q,k\}}^{(12)} \\ W_{\{q,k\}}^{(21)} & W_{\{q,k\}}^{(22)} \end{pmatrix} \begin{pmatrix} x_m^{(1)} \\ x_m^{(2)} \end{pmatrix} \end{equation}\]Relative position embedding을 통합하는 것은 간단하다. Affine-transform된 단어 임베딩 벡터를 위치 인덱스의 각도 배수만큼 회전하면 된다.
General form
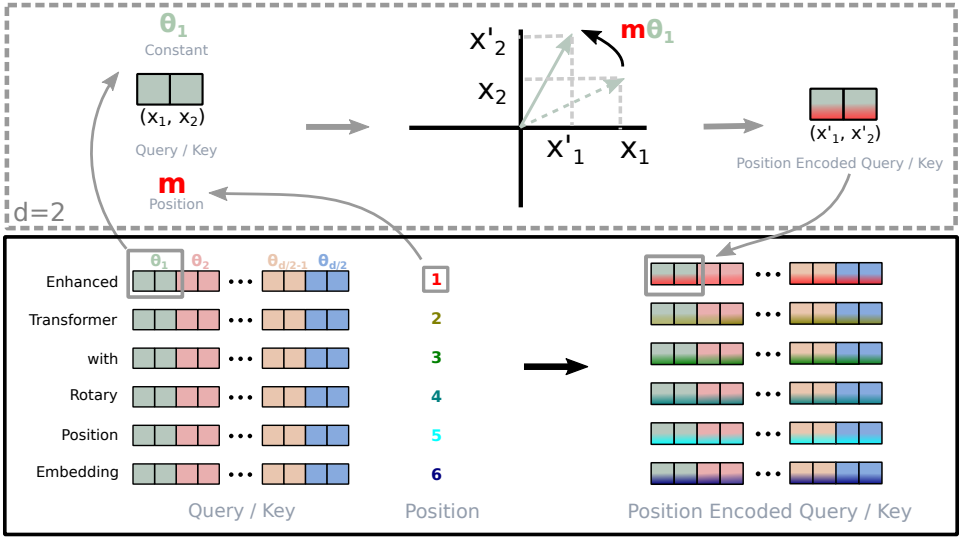
2차원에서 결과를 $d$가 짝수인 모든 $\mathbf{x}_i \in \mathbb{R}^d$로 일반화하기 위해, $d$차원 공간을 $d/2$개의 부분 공간으로 나누고 내적의 선형성을 이용해 부분 공간을 결합하여 \(f_{\{q,k\}}\)를 다음과 같이 바꾼다.
Self-attention에 RoPE를 적용하면 다음과 같다.
\[\begin{equation} \mathbf{q}_m^\top \mathbf{k}_n = (\mathbf{R}_{\Theta, m}^d \mathbf{W}_q \mathbf{x}_m)^\top (\mathbf{R}_{\Theta, n}^d \mathbf{W}_k \mathbf{x}_n) = \mathbf{x}_m^\top \mathbf{W}_q^\top \mathbf{R}_{\Theta, n-m}^d \mathbf{W}_k \mathbf{x}_n \end{equation}\]\(\mathbf{R}_{\Theta}^d\)는 직교 행렬이므로 위치 정보를 인코딩하는 동안 안정성을 보장한다.
\(\mathbf{R}_{\Theta}^d\)의 원소가 대부분 0이기 때문에 위와 같이 행렬 곱셈을 직접 적용하는 것은 계산적으로 효율적이지 않다. 그 대신 다음과 같이 효율적으로 계산할 수 있다.
\[\begin{equation} \mathbf{R}_{\Theta, m}^d \mathbf{x} = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ \vdots \\ x_{d-1} \\ x_d \end{pmatrix} \otimes \begin{pmatrix} \cos m \theta_1 \\ \cos m \theta_1 \\ \cos m \theta_2 \\ \cos m \theta_2 \\ \vdots \\ \cos m \theta_{d/2} \\ \cos m \theta_{d/2} \end{pmatrix} + \begin{pmatrix} -x_2 \\ x_1 \\ -x_4 \\ x_3 \\ \vdots \\ -x_d \\ x_{d-1} \end{pmatrix} \otimes \begin{pmatrix} \sin m \theta_1 \\ \sin m \theta_1 \\ \sin m \theta_2 \\ \sin m \theta_2 \\ \vdots \\ \sin m \theta_{d/2} \\ \sin m \theta_{d/2} \end{pmatrix} \end{equation}\]기존 position embedding들의 가산적 특성과 대조적으로 RoPE는 곱셈적이다. 또한, RoPE는 self-attention과 함께 적용될 때 가산적인 위치 인코딩을 변형하는 대신 회전 행렬 곱을 통해 자연스럽게 상대적 위치 정보를 통합한다.
3. Properties of RoPE
Long-term decay
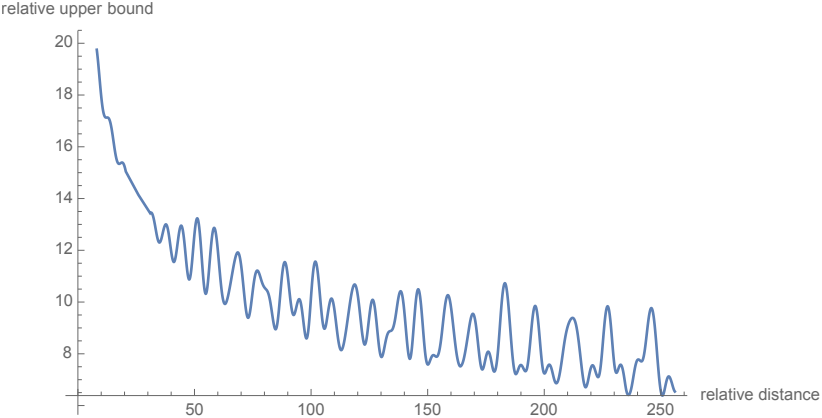
저자들은 Transformer를 따라 $\theta_i = 10000^{−2i/d}$로 설정했으며, 이 설정은 long-term decay 속성을 제공한다. 즉, 상대적 위치가 증가하면 내적이 감소한다. 이 속성은 상대적 거리가 긴 토큰 쌍은 연결이 적어야 한다는 직관과 일치한다.
RoPE with linear attention
Self-attention은 다음과 같이 더 일반적인 형태로 다시 쓸 수 있다.
\[\begin{equation} \textrm{Attention} (\mathbf{Q}, \mathbf{K}, \mathbf{V})_m = \frac{\sum_{n=1}^N \textrm{sim} (\mathbf{q}_m, \mathbf{k}_n) \mathbf{v}_n}{\sum_{n=1}^N \textrm{sim} (\mathbf{q}_m, \mathbf{k}_n)} \end{equation}\]원래의 self-attention은 \(\textrm{sim} (\mathbf{q}_m, \mathbf{k}_n) = \exp (\mathbf{q}_m^\top \mathbf{k}_n / \sqrt{d})\)를 선택하며, 모든 토큰 쌍에 대해 query와 key의 내적을 계산해야 하기 때문에 복잡도가 $O(N^2)$이다. Linear attention은 다음과 같다.
\[\begin{equation} \textrm{Attention} (\mathbf{Q}, \mathbf{K}, \mathbf{V})_m = \frac{\sum_{n=1}^N \phi (\mathbf{q}_m)^\top \psi (\mathbf{k}_n) \mathbf{v}_n}{\sum_{n=1}^N \phi (\mathbf{q}_m)^\top \psi (\mathbf{k}_n)} \end{equation}\]$\phi (\cdot)$와 $\psi (\cdot)$는 일반적으로 non-negative function이다. RoPE는 회전을 통해 위치 정보를 주입하므로 hidden representation의 norm이 변경되지 않는다. 따라서 회전 행렬에 non-negative function의 출력을 곱하여 RoPE를 linear attention과 결합할 수 있다.
\[\begin{equation} \textrm{Attention} (\mathbf{Q}, \mathbf{K}, \mathbf{V})_m = \frac{\sum_{n=1}^N (\mathbf{R}_{\Theta, m}^d \phi (\mathbf{q}_m))^\top (\mathbf{R}_{\Theta, n}^d \psi (\mathbf{k}_n)) \mathbf{v}_n}{\sum_{n=1}^N \phi (\mathbf{q}_m)^\top \psi (\mathbf{k}_n)} \end{equation}\]분자의 합에 음수 항이 포함될 수 있다. 각 value \(\mathbf{v}_i\)에 대한 가중치는 엄격하게 정규화되지 않았지만, 계산이 여전히 value의 중요성을 모델링할 수 있다.
Experiments
1. Machine Translation
다음은 WMT 2014 English-German 번역 성능을 Transformer와 비교한 표이다.

2. Pre-training Language Modeling
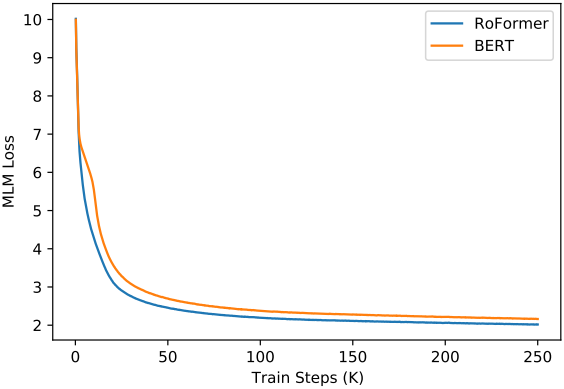
다음은 BERT와 RoFormer의 학습 loss를 비교한 그래프이다.
3. Fine-tuning on GLUE tasks
다음은 GLUE task에 fine-tuning한 RoFormer와 BERT를 비교한 표이다.

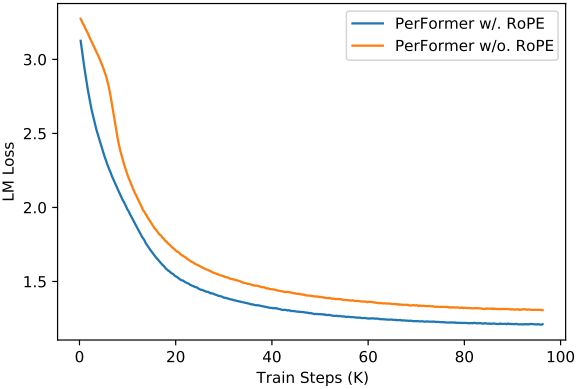
4. Performer with RoPE
다음은 RoPE 유무에 따른 PerFormer의 학습 loss를 비교한 그래프이다.
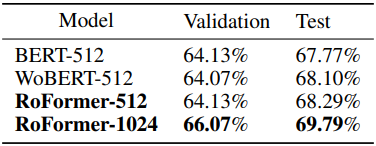
5. Evaluation on Chinese Data
다음은 중국어 데이터로 사전 학습시킨 RoFormer를 BERT, WoBERT와 CAIL2019-SCM task에서 비교한 표이다. (BERT와 WoBERT는 absolute position embedding 사용)