[논문리뷰] Reinforcement Learning Teachers of Test Time Scaling

arXiv 2025. [Paper] [Page] [Github]
Edoardo Cetin, Tianyu Zhao, Yujin Tang
Sakana AI
10 Jun 2025

Introduction

강화학습(RL)에서 탐색(exploration)은 핵심적인 과제 중 하나이다. Reward가 sparse할 경우, 에이전트가 초기 state에서 주어진 task를 해결할 수 있는 능력이 없다면 학습 신호를 전혀 제공할 수 없다. 최근에는 언어 모델(LM)의 확장으로서 RL 추론이 떠오르면서 탐색 문제는 다시 중요한 과제로 떠오르고 있다.

RL의 대표적인 동기는, reward function에 의해 유도되는 부분적인 해법으로부터 출발하여 완전히 새로운 task를 처음부터 학습할 수 있다는 가능성이다. 그러나 RL 추론 프레임워크에서는 일종의 정답 여부만을 나타내는 one-hot reward를 사용하기 때문에, dense한 학습 신호를 제공하지 못하고, 대신 초기 모델이 시도한 응답 중 정답에만 reward를 부여하는 식으로 작동한다. 이는 언어 모델의 초기 잠재 능력을 넘어선 일반화를 이루지 못하게 만든다. 그 결과, 이러한 방식은 주로 이미 강력하고 성능이 좋은 대형 모델에서만 일관된 성능 향상을 보여준다.

이러한 근본적인 한계와 RL의 학습 불안정성으로 인해 distillation은 현재 추론 패러다임의 또 다른 구성 요소로 등장했다. 이 경우 RL로 학습된 LM의 test-time 역할은 student가 새로운 문제를 풀 수 있도록 추론 설명을 제공하는 teacher 역할을 하는 것이다. 이 teacher-student 패러다임은 더 작고 성능이 낮은 모델을 학습시키기 위해 널리 사용될 뿐만 아니라, 향후 RL iteration에서 더 나은 최종 수렴을 달성하기 위해 teacher의 초기 체크포인트를 student로 삼아 cold-start하는 데에도 활용된다. 그러나 정확성 기반 reward로 강화된 문제 해결 능력은 distillation의 목표와 완전히 일치하지 않는다. 이러한 불일치를 설명하기 위해 현재 파이프라인은 teacher 출력의 휴리스틱 기반 후처리에 크게 의존한다.

본 논문은 효과적인 distillation을 도출하도록 특별히 학습된 Reinforcement Learned Teacher (RLT)를 통해 RL의 탐색 과제를 피하는 프레임워크를 제안하였다. 저자들의 주요 직관은 간단하다. 실제 teacher의 능력은 복잡한 정리, 증명 또는 답을 스스로 생각해 낼 수 있는지 여부로 측정되지 않는다. 중요한 것은 쉽게 구할 수 있는 student에게 유익한 설명을 고안해 낼 수 있는 능력이다. 따라서 기존의 RL 추론 프레임워크에서 벗어나, 모델에게 먼저 생각을 하고 처음으로 새로운 해설을 제시하도록 과제를 부여한다. 대신, RL teacher는 문제의 해결책이 이미 주어진 프롬프트에 있는 상황에서 효과적인 설명을 제공하는 더 쉬운 문제를 맡는다. Student의 log probability를 사용하여 dense reward를 제공하는 RLT를 학습시켜 teacher의 설명에서 각 문제의 GT 해설에 대한 학생의 이해도와 설명 자체의 논리적 비약에 대한 해석 가능성을 평가한다.

본 논문은 70억 개의 파라미터를 갖는 가벼운 RLT의 출력으로 student를 distillation함으로써, 훨씬 더 많은 파라미터를 갖는 추론 언어 모델에 의존하는 기존 파이프라인보다 훨씬 높은 성능을 보여주었다. RLT의 설명을 distillation하여 32B student를 학습시키고 기존 RL 최적화를 cold-start하는 경우에도 탁월한 이점을 제공한다. 전반적으로, 이러한 결과는 더 강력하고, 더 작으며, 재사용성이 높은 전문화된 teacher에 초점을 맞춤으로써 RL의 막대한 비용을 극복하는 동시에, 값비싼 휴리스틱 기반 distillation 파이프라인에 대한 현재의 의존성을 제거하였다.

Inducing reasoning in language models

1. Reinforcement learning

최근 DeepSeek R1은 증명 가능한 해설 \(\{s_1, \ldots, s_N\}\)이 주어진 질문 집합 $$D = {q_1, \ldots, q_N}$으로 LM을 fine-tuning하여, 효과적인 추론 능력을 이끌어내고, 어려운 수학 및 코딩 task에서 성능을 크게 향상시킬 수 있음을 보여주었다. DeepSeek R1의 학습은 GRPO라는 online RL 알고리즘으로 수행하며, 이는 critic 모델을 사용하지 않고 단순한 몬테카를로 value 추정 방식을 사용한다.

GRPO는 LM $\pi_\theta$가 샘플링된 각 질문 $q \in D$에 대해 $G \gg 1$개의 그룹화된 출력 세트 \(o_1, \ldots, o_G\)를 생성하도록 하여 다음 objective를 최적화한다.

\[\begin{equation} J(\theta) = \mathbb{E}_{q \sim D, \{o\}_1^G \sim \pi_\theta (\cdot \vert q)} \left[ \frac{1}{G} \sum_{i=1}^G (A_i - \beta \mathbb{D}_\textrm{KL} (\pi_\theta \, \| \, \pi_\textrm{ref})) \right] \end{equation}\]

여기서 advantage $A_i$는 각 그룹 내에서 각 출력의 reward $r_i$를 정규화하여 얻는다.

\[\begin{equation} A_i = \frac{r_i - \textrm{mean}(\{r_1, \ldots, r_G\})}{\textrm{std}(\{r_1, \ldots, r_G\})} \end{equation}\]

디자인의 핵심 구성 요소는 LM에게 생성된 각 출력 $o_i$를 <think>와 <solution> 태그로 구분된 두 개의 형식화된 섹션 $t_{o_i}$ $s_{o_i}$로 분해하도록 요청하는 시스템 프롬프트이다. 이러한 구조는 형식화되지 않은 출력에는 $r_i = −1$, 틀렸지만 형식화된 출력에는 $r_i = −0.5$, 그리고 정확하고 형식화된 출력에는 $r_i = 1$의 reward를 할당함으로써 강제된다. 이 전략으로 학습한 결과, 언어 모델의 출력 길이가 생각, 검증, 수정 단계가 등장함에 따라 점진적으로 증가하며, 이는 인간의 사고 과정을 반영하는 것과 유사하다.

2. Supervised distillation

Supervised distillation은 RL의 단점을 보완하기 위해 최근 추론 모델을 학습시키는 데 사용되는 또 다른 중요한 단계이다. 위의 $J(\theta)$와 같은 online RL objective가 붕괴를 방지하려면 모델이 초기화 시 0이 아닌 gradient를 가진 해설을 생성할 수 있는 어느 정도의 확률을 이미 가지고 있어야 한다. 이러한 속성 때문에 RL objective는 모델의 gradient에 해설의 정보를 항상 포함하는 cross-entropy objective보다 훨씬 적용하기 어렵다.

이러한 이분법의 결과로, supervised learning을 사용하여 대규모 RL 학습된 LM의 추론 흔적을 distillation하는 것은 비용이 저렴할 뿐만 아니라 작고 성능이 낮은 모델에서 추론을 유도하는 데 RL 자체를 수행하는 것보다 훨씬 더 효과적이다. 또한 RL은 특히 장시간 학습 동안 불안정성과 출력 저하가 발생하기 쉽다. 이러한 한계점으로 인해 DeepSeek R1은 여러 iteration에 걸쳐 RL 학습을 수행한다. 각 중간 iteration의 끝에서 RL 학습된 모델을 사용하여 원래 초기 체크포인트의 cold-starting에 사용되는 distillation 데이터셋을 다시 수집하고 다음 RL iteration을 위한 더 강력한 초기화 체크포인트를 얻는 방식으로 수행된다.

Distillation 프롬프트 데이터셋 \(D_\textrm{SD} = \{d_1, \ldots, d_N\}\)을 구성하는 것은 추론 시스템 프롬프트와 함께 RL로 학습된 LM \(\pi_\theta\)를 사용하여 증명 가능한 질문의 코퍼스에 답하는 것을 포함하며, 이는 여러 휴리스틱으로 선택할 수 있다. 각 질문에 대한 LM의 출력 \(o \sim \pi_\theta (\cdot \vert q)\)은 정확성을 보장하기 위해 GT 해설과 비교하여 필터링되며, 추가적인 수동 개선 단계를 통해 후처리된다.

Reinforcement learning teachers

1. The implications of training teacher models as students

저자들은 현대 추론 프레임워크에서 LM이 수행할 수 있는 역할을 학습 역할과 추론 역할로 구분하였다. RL 학습 후 LM \(\pi_\theta\)는 종종 직접 배포되지 않고, 약한 모델을 fine-tuning하고 향후 RL 반복을 cold-start하기 위한 distillation 데이터셋을 얻는 데 사용된다. 따라서 이러한 모델은 향후 학습 모델 $\pi$가 학습할 수 있도록 설명을 제공하는 teacher 역할을 할 수 있다.

이러한 teacher-student 패러다임은 RL 학습에 사용되는 objective와 teacher의 test-time 역할 간의 잠재적 불일치를 드러낸다. 전통적인 환경에서 teacher는 어려운 문제를 처음부터 해결하는 능력을 향상시키기 위해 sparse한 정확성 reward를 통해 학습받는다. 이는 내재적인 탐색 과제로 인해 기본 모델의 원래 역량을 넘어서는 task에 RL 학습을 적용하는 것을 불가능하게 할 뿐만 아니라, teacher의 실제 최종 목표, 즉 student가 스스로 해설을 도출하는 데 필요한 기술을 학습할 수 있는 출력을 생성하는 것과도 일치하지 않는다.

본 논문은 RL의 탐색 과제를 피하고 이러한 목표 불일치를 해소하는, teacher로 사용될 RL 추론 모델을 위한 새로운 학습 프레임워크를 제안하였다. 이 프레임워크는 훨씬 쉬운 task 구성, dense한 reward, 그리고 신중하게 설계된 학습 레시피로 구성되어 있으며, 이를 통해 새로운 유형의 전문화된 Reinforcement Learned Teacher (RLT)를 학습시킬 수 있다.

2. Aligning the task of teacher models

기존 RL 패러다임에서 각 문제에 대한 해설 $s_i$는 모델에 명시적으로 제공되지 않고 LM의 출력 $s_{o_i}$ 내에서 해당 해설의 정확성을 확인하는 데만 사용된다. 해설에 대한 직접 액세스나 정보를 배제하면 완전히 새로운 테스트 문제를 처음부터 푸는 test-time objective와 학습이 일치하지만, 모델이 첫 번째 성공적인 시도 전까지 gradient를 받지 못하기 때문에 탐색이 어려워지는 것이다.

그러나 저자들의 주요 관찰은 알려진 해설이 있는 문제에 대한 효과적인 distillation 데이터셋 \(D_\textrm{SD}\)를 생성하는 test-time teaching objective는 그러한 해설에 대한 액세스를 명시적으로 제공함으로써 크게 촉진될 수 있다는 것이다. 쉽게 사용할 수 있는 해설에 대한 액세스를 의지할 수 있고, 따라서 student에게 설명이 얼마나 유익한지에 전적으로 집중할 수 있게 된다.

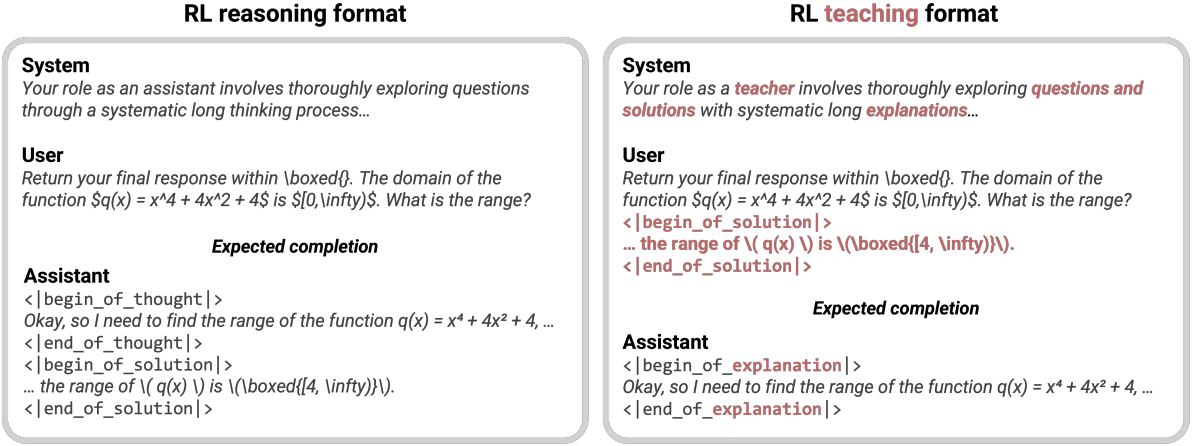
이를 위해 위 그림에서 볼 수 있듯이, RLT는 새로운 형식 스타일을 사용하여 각 문제에 대한 질문과 해설을 모두 입력으로 제공하고, 두 가지를 연결하는 step-by-step 설명을 작성하도록 과제를 부여받는다. 저자들은 자연스러운 진행을 유지하면서 teacher의 출력을 학생의 distillation을 위해 직접 재사용할 수 있도록 프롬프트를 설계하였다. 즉, 각 출력을 생성하기 전에 RLT의 시스템 프롬프트와 입력 질문에 solution 토큰 $s_i$와 solution 태그를 추가한다.

3. Evaluating the quality of explanations

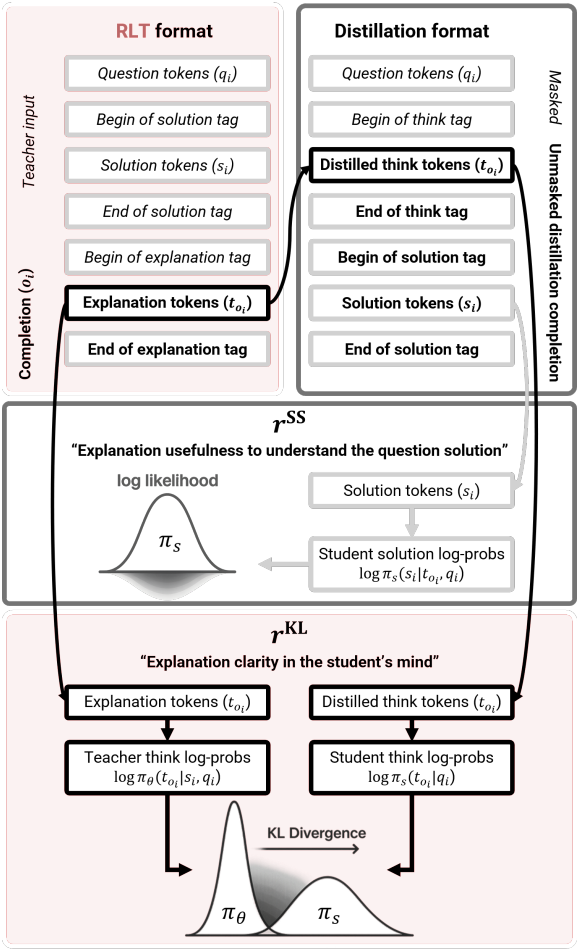
RLT를 학습시키기 위한 reward function은 student $\pi$가 해설 $s_i$를 회복하도록 유도하는 두 개의 항으로 구성되며, 이는 student의 관점에서 질문 자체의 논리적 연속이기도 하다. 특히, teacher \(\pi_\theta\)의 각 출력 $o_i$에 대해 think 토큰 $t_{o_i}$를 추출하고, 질문 $q_i$를 앞에 붙이고 해설 $s_i$를 뒤에 붙여 student 증류 프롬프트 $d_i$를 구성한다. 위 그림에서 볼 수 있듯이, 각 distillation 프롬프트는 student 모델에 입력으로 제공되어 토큰별 log probability 집합이 얻어지며, 이는 다음과 같이 두 개의 reward 항으로 처리된다.

\(r_i^\textrm{SS}\)는 주어진 문제 $q_i$와 맥락 내 think 토큰 $t_{o_i}$에 대한 student의 해설 $s_i$에 대한 이해도를 정량화한다. 이 첫 번째 reward 항은 solution 토큰에 대한 student의 log probability로 계산된다.

\[\begin{equation} r^\textrm{SS} (o_i, s_i, q_i) = \textrm{avg} \{ \textrm{log} \pi_s^{s_i} \} + \alpha \textrm{min} \{ \textrm{log} \pi_s^{s_i} \} \\ \textrm{where} \quad \pi_s^{s_i} = \pi_s (s_i \, \vert \, t_{o_i}, q_i) \end{equation}\]

\(r_i^\textrm{KL}\)는 think 토큰 자체가 teacher의 관점과 비교하여 student의 관점에서 해석 가능한 논리적 연속인지 여부를 정량화한다. 이 두 번째 reward 항은 teacher의 분포와 student의 분포 사이의 think 토큰에 대한 KL divergence를 계산한다.

\[\begin{equation} r^\textrm{KL} (o_i, s_i, q_i) = \textrm{avg} \left\{ \mathbb{D}_\textrm{KL} \left( \pi_\theta^{t_{o_i}} \, \| \, \pi_s^{t_{o_i}} \right) \right\} + \textrm{max} \left\{ \mathbb{D}_\textrm{KL} \left( \pi_\theta^{t_{o_i}} \, \| \, \pi_s^{t_{o_i}} \right) \right\} \\ \textrm{where} \quad \pi_s^{t_{o_i}} = \pi_s (t_{o_i} \, \vert \, q_i), \quad \pi_\theta^{t_{o_i}} = \pi_\theta (t_{o_i} \, \vert \, s_i, q_i) \end{equation}\]

RLT reward는 이 두 항을 가중치 계수 $\lambda$와 결합하여 얻는다.

\[\begin{equation} r_i^\textrm{RLT} = r^\textrm{SS} (o_i, s_i, q_i) - \lambda r^\textrm{KL} (o_i, s_i, q_i) \end{equation}\]

\(r_i^\textrm{SS}\)를 최적화하면 student가 해설 $s_i$에 도달할 likelihood를 최대화하는 think 토큰 $t_{o_i}$를 포함하는 설명이 생성된다. 그러나 이 항만으로는 student를 step-by-step으로 가이드하는 설명과 학습할 수 있는 논리적 경로 없이 해설의 likelihood를 높이는 설명을 구분할 수 없다. 후자의 극단적인 예로는 likelihood를 높이기 위해 단순히 solution 토큰을 반복하는 설명으로, 새로운 문제에 접근할 때 적용할 수 있는 추론 방법의 일반적인 예를 제시하지 못하는 것이다.

따라서 \(r_i^\textrm{KL}\)을 도입함으로써 정확히 이 간극을 메울 수 있으며, 이는 distillation 프롬프트 $d_i$ 내에서 질문 $q_i$와 이전 think 토큰들만을 컨텍스트로 사용할 때, 출력 설명의 각 think 토큰이 너무 낮은 확률을 가지지 않도록 teacher의 분포를 student의 분포에 맞춰 조정하는 효과를 가진다. 즉, 이 항을 도입함으로써 teacher의 설명이 따라가는 논리적 경로의 각 단계가 학생의 기존 이해와 질문만을 바탕으로 보았을 때 여전히 의미가 있도록 정규화하는 것이다.

또한, 평균뿐 아니라 min/max 연산과 결합함으로써 reward가 어떤 개별 토큰도 무시하지 않도록 하여, 해설의 길이나 think 토큰의 수에 관계없이 공정하게 작동하도록 보장한다. 이러한 고려 없이 개별 논리 단계를 생략하면 해설의 길이에 따라 \(r_i^\textrm{SS}\)가 편향되거나, teacher가 어려우나 필수적인 논리 단계를 피하면서도 \(r_i^\textrm{KL}\)의 영향을 줄이기 위해 지나치게 긴 설명을 선호하는 문제가 발생할 수 있다.

4. Pulling everything together: the RLT training paradigm

RLT 프레임워크는 LM의 컨디셔닝 및 reward에 대한 최소한의 수정만으로 모든 RL 알고리즘과 함께 사용할 수 있다. 본 논문에서는 간단한 GRPO 레시피를 사용하여 다음과 같은 objective를 도출하였다.

\[\begin{equation} J^\textrm{RLT} (\theta) = \mathbb{E}_{q, s \sim D, \{o\}_1^G \sim \pi_\theta (\cdot \vert s, q)} \left[ \frac{1}{G} \sum_{i=1}^G (A_i^\textrm{RLT} - \beta \mathbb{D}_\textrm{KL} (\pi_\theta \, \| \, \pi_\textrm{ref})) \right] \end{equation}\]

정확성 기반 reward와 달리, 이 학습 신호는 본질적으로 dense하여 task 전문성을 달성하지 않더라도 RLT 출력에 대한 유익한 순위를 제공한다. 이러한 근본적인 차이점은 최적화를 크게 촉진한다.

Experiments

1. Test-time reasoning across teachers and students

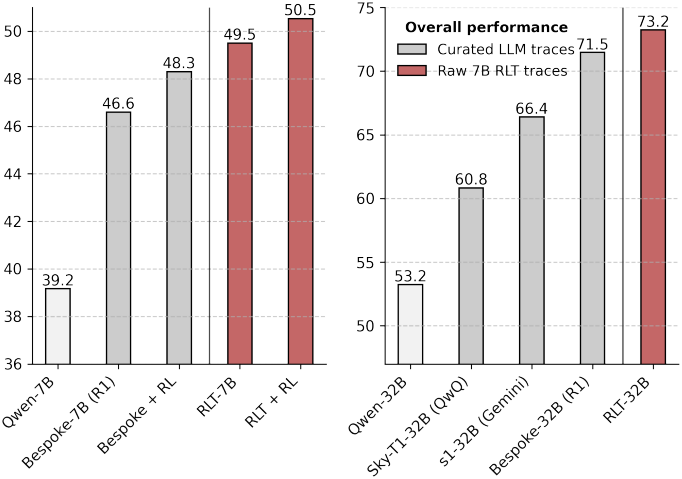
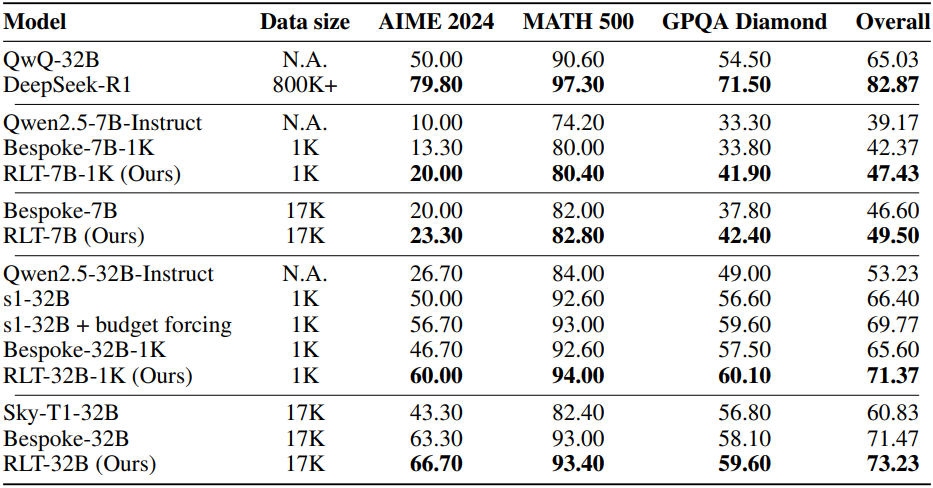
다음은 기존 distillation 파이프라인들과 성능을 비교한 결과이다.

2. RLTs to cold-start RL

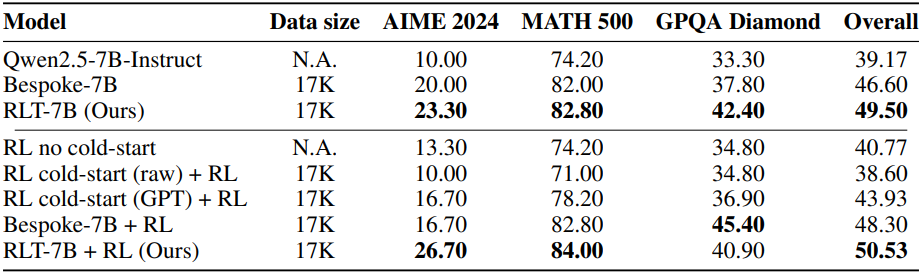
다음은 기존 RL을 cold-start하였을 때의 성능을 기존 distillation 파이프라인들과 비교한 결과이다.

3. Out-of-domain zero-shot transfer

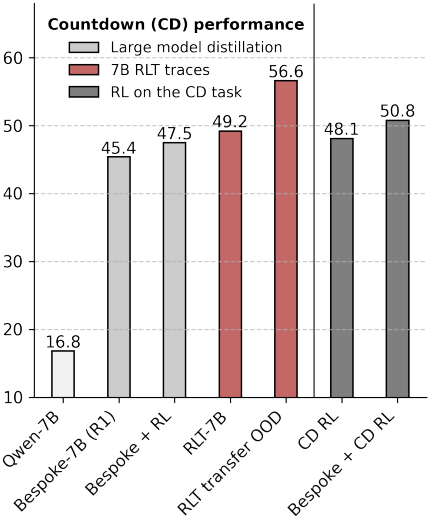
다음은 out-of-distribution 성능을 비교한 그래프이다.

4. Explanation reward analysis

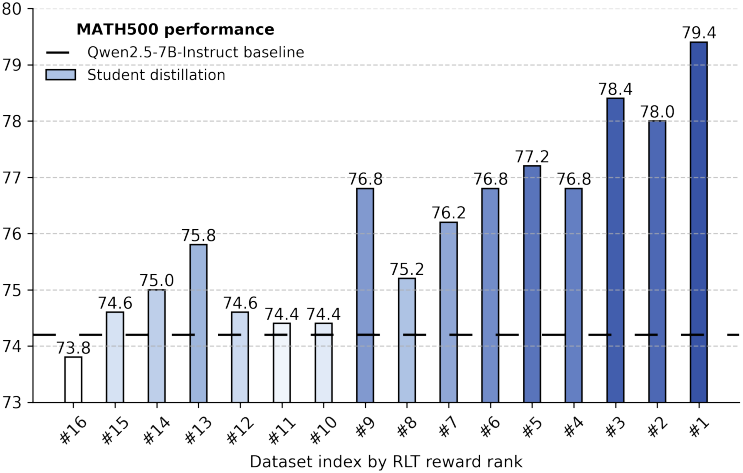
다음은 상대적인 RLT reward를 기준으로 distillation 데이터셋을 16개의 그룹으로 나누고, 각 데이터셋으로 학습한 후의 성능을 RLT reward에 대하여 비교한 그래프이다.

다음은 후처리한 후의 R1 출력과 RLT의 설명을 비교한 예시이다.