[논문리뷰] Scalable Adaptive Computation for Iterative Generation (RIN)

ICML 2023. [Paper] [Github]
Allan Jabri, David Fleet, Ting Chen
Google Research, Brain Team | Department of EECS, UC Berkeley
22 Dec 2022

Introduction

효과적인 신경망 아키텍처의 설계는 딥러닝의 성공에 결정적이었다. 최신 가속기 하드웨어의 영향을 받은 CNN과 Transformer와 같은 주요 아키텍처는 입력 데이터 (ex. 이미지 픽셀, 이미지 패치, 토큰 시퀀스)에 대해 고정되고 균일한 방식으로 계산을 할당한다. 자연 데이터의 정보는 종종 고르지 않게 분포되거나 중복성을 나타내므로 확장성을 향상시키기 위해 적응형 방식으로 계산을 할당하는 방법을 묻는 것이 중요하다. 이전 연구들에서는 보조 메모리나 global unit이 있는 네트워크와 같이 보다 역동적이고 입력이 분리된 계산을 연구했지만 적응형 계산을 활용하여 큰 입력 및 출력 space가 있는 task로 효과적으로 확장하는 일반 아키텍처는 아직 파악하기 어렵다.

본 논문에서는 이미지와 동영상 생성과 같은 고차원 생성 모델링 task에서 나타나는 이 문제를 고려한다. 예를 들어 간단한 배경이 있는 이미지를 생성할 때 적응형 아키텍처는 이상적으로는 구조가 거의 없거나 전혀 없는 영역(ex. 하늘)이 아닌 복잡한 개체와 텍스처가 있는 영역에 계산을 할당할 수 있어야 한다. 동영상을 생성할 때 프레임 간 중복성을 활용하여 정적인 영역에 더 적은 계산을 할당해야 한다. 이러한 불균일한 계산 할당은 고차원 데이터에서 더 중요하지만, 밀도가 높은 행렬 곱셈을 사용하는 고정 계산 그래프에 대한 선호도를 고려할 때 최신 하드웨어에서는 이를 효율적으로 달성하는 것이 어렵다.

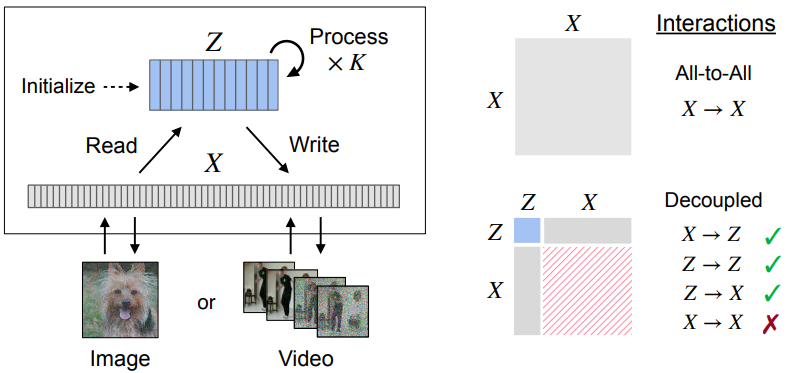
본 논문은 이 문제를 해결하기 위해 위 그림과 같은 Recurrent Interface Networks (RIN)이라는 새로운 아키텍처를 도입했다. RIN에서 hidden unit은 interface와 latent로 분할된다. Interface unit은 입력에 로컬로 연결되며 입력 크기에 따라 선형적으로 증가한다. 반면 latent는 입력 space에서 분리되어 보다 간결한 표현을 형성한다.

계산은 “read-process-write” block의 스택에서 진행된다. 각 block에서는 고용량 글로벌 처리를 위해 interface에서 정보를 선택적으로 읽어 latent로 전송한 다음, incremental update가 interface로 다시 전송된다. Latent와 interface 간의 교대 계산을 통해 로컬 레벨과 글로벌 레벨에서 정보를 처리하고 더 나은 라우팅을 위해 컨텍스트를 축적할 수 있다. 따라서 RIN은 균일한 모델보다 계산을 더 효율적으로 할당하며, 자연 데이터에서 흔히 볼 수 있듯이 정보가 입력에 고르지 않게 분산되거나 중복될 때 특히 잘 확장된다.

정보의 반복적인 라우팅에는 약간의 오버헤드가 필요하며, 이는 특히 얕은 네트워크의 경우 latent가 컨텍스트 없이 초기화되면 잠재적인 효율성 향상을 무색하게 할 수 있다. 이 비용은 네트워크 입력이 점진적으로 변경되고 지속적인 컨텍스트가 반복을 통해 활용되어 사실상 더 깊은 네트워크를 형성할 수 있는 recurrent한 계산과 관련된 시나리오에서 줄일 수 있다.

구체적인 응용으로 denoising diffusion model을 사용한 이미지 및 비디오의 반복적인 생성을 고려한다. Recurrence를 활용하기 위해 latent가 효과적인 정보 라우팅 비용을 줄이기 위한 “warm-start” 메커니즘으로 latent self-conditioning을 제안한다. 각 iteration에서 latent를 다시 초기화하는 대신 이전 iteration의 latent를 추가 컨텍스트로 사용한다. RNN과 유사하지만 시간에 따른 backpropagation이 필요하지 않다.

Method

1. Overview

RIN에서 interface는 입력 공간에 로컬로 연결되고 토큰화 형식(ex. 패치 임베딩)을 통해 초기화되는 반면 latent는 데이터에서 분리되고 학습 가능한 임베딩으로 초기화된다. 기본 RIN 블록은 interface와 latent 간에 정보를 라우팅하여 계산을 할당한다. 여러 block을 쌓음으로써 bottom-up 및 top-down 컨텍스트가 다음 block의 라우팅을 알릴 수 있도록 interface와 latent를 점진적으로 업데이트할 수 있다 (위 그림 참고). 마지막으로 readout function (ex. linear projection)은 최종 interface 표현에서 네트워크의 출력을 생성한다.

Interface는 데이터에 연결되어 있기 때문에 입력 크기에 따라 선형적으로 증가하고 크기가 클 수 있지만, latent unit의 수는 훨씬 작을 수 있다. Interface에서 직접 작동하는 계산(ex. 토큰화, 읽기, 쓰기)은 입력 space 전체에서 균일하지만 균일한 계산의 양을 제한하기 위해 상대적으로 가볍게 설계되었다. 고용량 처리는 latent를 위해 남겨 두며, interface에서 선택적으로 정보를 읽어서 형성되므로 대부분의 계산이 입력의 구조와 내용에 맞게 조정될 수 있다. 입력에 중복성이 있는 경우 latent는 보다 효율적인 처리를 위해 입력을 추가로 압축할 수 있다.

U-Net과 같은 convolutional network와 비교할 때 RIN은 전역 계산을 위해 고정된 downsampling 또는 upsampling에 의존하지 않는다. Transformer와 비교하여 RIN은 입력 도메인 전체에서 유사한 유연성을 위해 positional encoding이 있는 토큰들의 집합에서 작동하지만 토큰당 컴퓨팅 및 메모리 요구 사항을 줄이기 위해 토큰에서 pairwise attention을 피한다. Perceiver와 같은 다른 분리된 아키텍처와 비교할 때 interface와 latent 사이의 교대 계산을 통해 엄청나게 큰 latent 집합 없이 보다 표현이 풍부한 라우팅이 가능한다.

RIN은 다재다능하지만 정보 라우팅을 추가로 준비하기 위해 영구 컨텍스트를 전파할 수 있도록 시간이 지남에 따라 입력이 점진적으로 변경될 수 있는 recurrent setting에서 이점이 더욱 두드러진다. 따라서 여기에서는 diffusion model을 사용하여 반복적인 생성에 RIN을 적용하는 데 중점을 둔다.

2. Iterative Generation with Diffusion Models

Diffusion model은 일련의 state transition을 학습하여 알려진 사전 분포의 noise $\epsilon$을 데이터 분포의 $x_0$에 매핑한다. Noise에서 데이터로의 이 reverse transition을 학습하기 위해 $x_0$에서 $x_t$로의 forward transition이 먼저 정의된다.

\[\begin{equation} x_t = \sqrt{\gamma(t)} x_0 + \sqrt{1 - \gamma(t)} \epsilon \end{equation}\]

$\epsilon \sim \mathcal{N}(0,I)$이고 $t \sim \mathcal{U}(0,1)$이며 $\gamma(t)$는 1에서 0으로 단조 감소하는 함수이다. $x_t$에서 $x_{t- \Delta}$로의 transition을 모델링하도록 직접 신경망을 학습시키는 대신, 신경망 $f(x_t, t)$가 $x_t$에서 $\epsilon$을 예측한 다음 $x_t$와 추정된 $\tilde{\epsilon}$에서 $x_{t- \Delta}$를 추정한다. $f(x_t, t)$를 위한 목적 함수는 다음과 같다.

\[\begin{equation} \mathbb{E}_{t \sim \mathcal{U}(0,1), \epsilon \sim \mathcal{N}(0,I)} \| f(\sqrt{\gamma(t)} x_0 + \sqrt{1 - \gamma(t)} \epsilon, t) - \epsilon \|^2 \end{equation}\]

학습된 모델에서 샘플을 생성하기 위해 일련의 state transition $x_1 \rightarrow x_{1 - \Delta} \rightarrow \cdots \rightarrow x_0$을 따른다. 이는 각 state $x_t$에서 반복적으로 $f$를 적용하여 $\epsilon$을 추정하고 DDPM의 transition 규칙을 사용하여 $x_{t-\Delta}$를 추정한다. $f$의 반복적인 적용을 통한 $x$의 점진적 개선은 RIN에 자연스럽게 적합하다. 네트워크는 noisy한 이미지 $x_t$, timestep $t$, 선택적 컨디셔닝 변수를 입력으로 사용하여 추정된 노이즈 $\tilde{\epsilon}$을 출력한다.

3. Elements of Recurrent Interface Networks

Interface Initialization

Interface는 입력 $x$를 $n$개의 벡터의 집합 $X \in \mathbb{R}^{n \times d}$에서 $x$를 토큰화하여 초기화된다. 예를 들어 ViT와 유사한 선형 패치 임베딩을 사용하여 이미지를 패치 토큰 집합으로 변환한다. 동영상의 경우 3D 패치를 사용한다. 위치를 나타내기 위해 패치 임베딩은 학습 가능한 위치 인코딩과 더해진다. 토큰화 외에도 모델은 도메인에 구애받지 않으며, 이는 $X$가 단순히 벡터 집합이기 때문이다.

Latent Initialization

Latent $Z \in \mathbb{R}^{m \times d’}$는 학습된 임베딩으로서 초기화되며, 입력에 독립적이다. 클래스 레이블이나 timestep $t$와 같은 컨디셔닝 변수는 임베딩에 매핑되며, 간단하게 latent들의 집합에 concat된다. $n$은 $x$의 크기에 선형인 반면, $m$은 입력 크기에서 분리되며 큰 입력의 경우에도 작게 유지될 수 있으며, 이는 라우팅이 처리를 위해 interface에서 정보를 적응적으로 선택하기 때문이다.

Core Computation Block

RIN 블록은 $X$에서 $Z$로 읽고, $Z$를 처리하고, 업데이트를 다시 $X$에 기록하여 정보를 라우팅한다. 저자들은 Transformer의 핵심 구성 요소로 이러한 연산을 구현한다.

\[\begin{aligned} \textrm{Read: } Z &= Z + \textrm{MHA} (Z, X) \\ Z &= Z + \textrm{MLP} (Z) \\ \textrm{Process: } Z &= Z + \textrm{MHA} (Z, Z) \\ [\times K] \;\; Z &= Z + \textrm{MLP} (Z) \\ \textrm{Write: } X &= X + \textrm{MHA} (X, Z) \\ X &= X + \textrm{MLP} (X) \\ \end{aligned}\]

$\textrm{MLP}$는 multi-layer perceptron이고 $\textrm{MHA} (Q, K)$는 query가 $Q$이고 key와 value가 $K$인 multi-head attention이다. Processing layer의 수 $K$는 interface와 latent들에서 발생하는 계산의 비율을 조절하는 데 사용된다. Hidden unit간의 정보 교환 관점에서 MHA는 벡터를 통해 정보를 전파한다 (즉, latent들 사이 또는 latent와 interface 사이). 반면 MLP(공유 가중치를 사용하여 벡터 방식으로 적용됨)는 채널을 통해 정보를 혼합한다. 여기서 interface에 대한 계산은 MHA 다음에 MLP가 오는 것처럼 쓰기 연산으로 접한다.

RIN block을 쌓아 latent가 컨텍스트를 축적하고 incremental update를 interface에 쓸 수 있도록 할 수 있다. 출력 예측을 생성하기 위해 해당 interface 토큰에 readout layer (ex. linear projection)을 적용하여 로컬 출력(ex. 이미지 또는 비디오 패치)을 예측한다. 그런 다음 로컬 출력이 결합되어 원하는 출력을 형성한다 (ex. 패치는 단순히 이미지로 재구성됨).

4. Latent Self-Conditioning

RIN은 라우팅 정보에 의존하여 컴퓨팅을 입력에 일부에 동적으로 할당한다. 효과적인 라우팅은 입력별 latent에 의존하며 입력별 latent는 interface 정보를 읽어서 구축된다. 이 반복적인 프로세스는 특히 네트워크가 컨텍스트 없이, 즉 “cold-start”에서 시작하는 경우 적응형 계산의 이점을 무색하게 할 수 있는 추가 비용을 발생시킬 수 있다. 직관적으로, 인간은 환경 변화에서 유사한 “cold-start” 문제에 직면하며 관련 정보를 추론하는 능력을 향상시키기 위해 새로운 상태에 점진적으로 익숙해져야 한다. “Warm-up”을 위한 충분한 시간 없이 컨텍스트가 빠르게 전환되면 반복적으로 비용이 많이 드는 적응에 직면하게 된다. RIN의 “warm-up” 비용은 글로벌 컨텍스트가 지속되는 동안 입력이 점진적으로 변경되는 순차적 계산 세팅으로 유사하게 줄일 수 있다. 저자들은 이러한 세팅에서 각 forward pass에 누적된 latent들에서 유용한 컨텍스트가 존재한다고 가정한다.

Warm-starting Latents

위와 같은 이유로 이전 step에서 계산된 latent들을 사용하여 latent들을 “warm-up”하는 것을 제안한다. 현재 timestep $t$에서의 초기 latent들은 입력에 독립적인 학습 가능한 임베딩 $Z_{emb}$과 $t’$에서의 이전 latent들의 변환($t’$에서 연관된 입력의 함수)의 합이다.

\[\begin{equation} Z_t = Z_{emb} + \textrm{LayerNorm} (Z_{t'} + \textrm{MLP} (Z_{t'})) \end{equation}\]

LayerNorm은 scaling과 bias가 모두 0으로 초기화되므로, 학습 초기에는 $Z_t = Z_{emb}$이다.

원칙적으로 이는 이전 timestep의 latent $Z_{t’}$의 존재성에 의존하고, 확장성을 방해할 수 있는 역전파를 통한 반복과 학습을 필요로 한다. Diffusion model의 주요 이점은 transition의 chain이 조건부로 독립적인 step으로 분해되어 저자들이 보존하고자 하는 고도로 병렬화 가능한 학습을 허용한다는 것이다. 이를 위해 시간 $t$에 대한 자체 unconditional한 예측으로 denoising network를 조절하는 self-conditioning 테크닉에서 영감을 얻는다.

조건부 denoising network $f(x_t, t, Z_{t’})$를 고려하자. 학습 중에 특정 확률로 $f(x_t, t, 0)$를 사용하여 직접 \(\tilde{\epsilon}_t\)를 계산한다. 반면에 $f(x_t, t, 0)$를 적용하여 $Z_{t’}$의 추정으로 latent $\tilde{Z}_t$를 얻고, $f(x_t, t, \textrm{sg}(\tilde{Z}_t))$로 예측값을 계산한다. 여기서 $\textrm{sg}$는 stop-gradient 연산으로, latent 추정에 역전파가 흐르지 못하도록 한다.

Inference 시에는 이전 timestep $t’$의 latent들을 직접 사용하여 현재 timestep $t$의 latent들을 초기화한다. 이 bootstrapping 절차는 학습 시간을 약간 증가시키지만 (stop-gradient로 인해 실제로는 25%보다 적음), inference 시간에 드는 비용은 무시할 수 있다. 데이터 레벨에서의 self-conditioning과 달리 여기서는 신경망의 latent 활성화를 조절하므로 이를 latent self-conditioning이라고 한다.

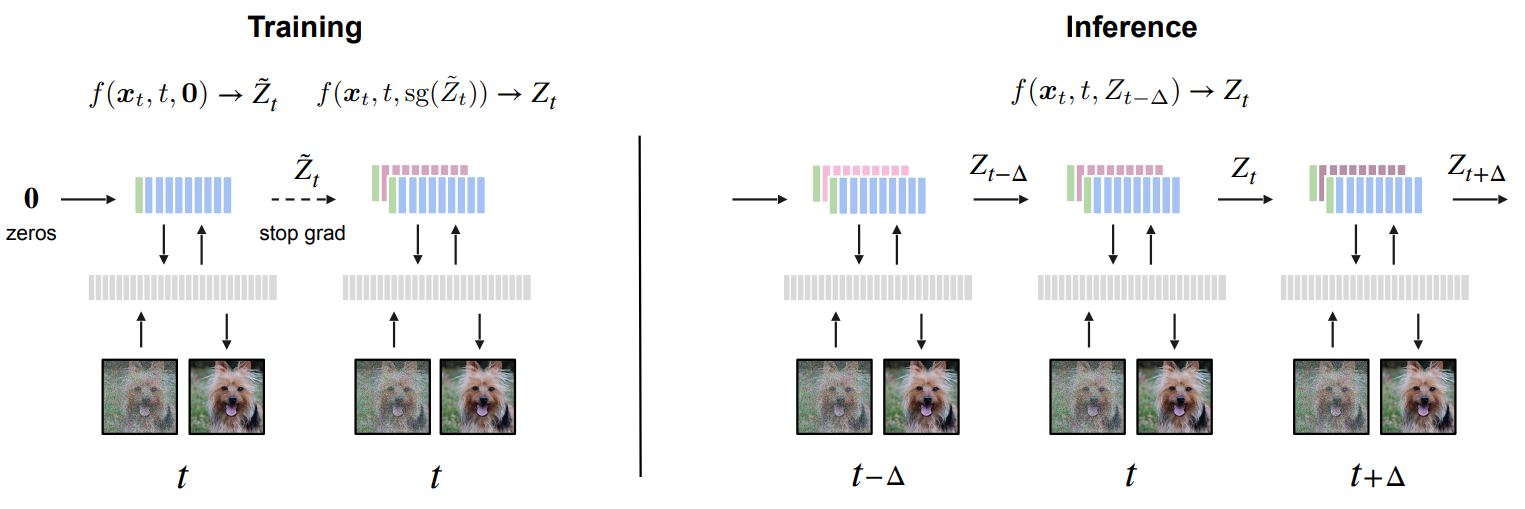
위 그림은 제안된 latent self-conditioning을 사용한 학습과 샘플링 과정을 나타낸 것이다. Algorithm 1과 2는 diffusion process의 학습과 샘플링에 대한 제안된 수정 사항을 보여준다

Experiments

1. Implementation Details

Sigma Noise Schedule

연속 시간 noise schedule 함수 $\gamma(t)$을 사용하며 cosine schedule을 기본으로 한다. 저자들은 cosine schedule이 가끔씩 고해상도 이미지에서 불안정하다는 것을 발견했으며, 이것이 굉장히 높거나 낮은 noise level을 샘플링할 확률이 상대적으로 높기 때문이라고 추측한다. 따라서 저자들은 시그모이드 함수 기반의 다른 schedule을 실험하였으며, 다양한 temperature를 사용하여 중간 noise level에 더 많은 가중치를 두었다. 실험 결과는 아래 그래프와 같다.

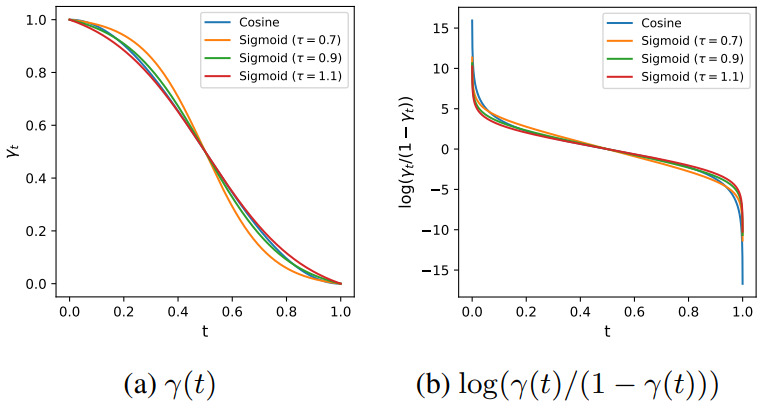
기본 temperature는 0.9으로 설정하였다.

Tokenization and Readout

이미지 생성의 경우, 겹치지 않는 패치들을 추출한 다음 linear projection을 통해 이미지를 토큰화한다. 64$\times$64, 128$\times$128 이미지는 패치 사이즈를 4로 두었으며, 256$\times$256 이미지는 패치 사이즈를 8로 두었다. 출력을 생성하기 위해 interface 토큰에 linear projection을 적용하고 각 project된 토큰을 unfold하여 예측된 패치들을 얻는다.

동영상의 경우, 이미지와 동일한 방식으로 예측을 생성한다. 16$\times$64$\times$64 크기의 입력의 경우 2$\times$4$\times$4 크기의 패치를 사용한다. 조건부 생성의 경우 학습 중에 입력의 리부로 컨텍스트 프레임을 제공받는다. 샘플링 중에는 컨텍스트 프레임이 고정된다.

위 표는 task에 따른 모델의 configuration을 비교한 것이다.

2. Experimental Setup

이미지 생성의 경우 ImageNet 데이터셋을 주로 사용한다. Center crop과 random left-right flipping만을 사용한다. CIFAR-10도 사용하여 모델이 작은 데이터셋에서 학습될 수 있음을 보인다. 평가의 경우, FID와 Inception Score를 metric으로 사용하며 5만 개의 샘플을 1000 step으로 생성하여 사용한다.

동영상 예측의 경우 16$\times$64$\times$64 해상도에서 Kinetics-600 데이터셋을 사용한다. 평가의 경우, FVD와 Inception Score를 사용하며 5만 개의 샘플을 400이나 1000 step으로 생성하여 사용한다.

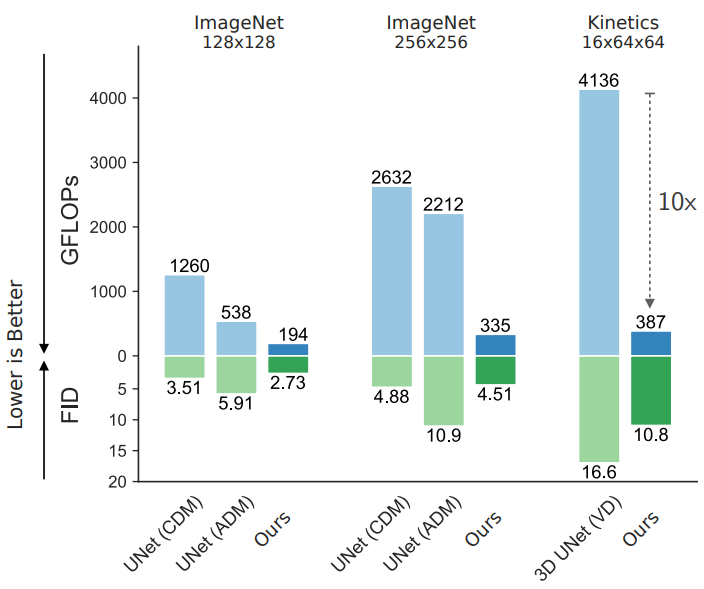
3. Comparison to SOTA

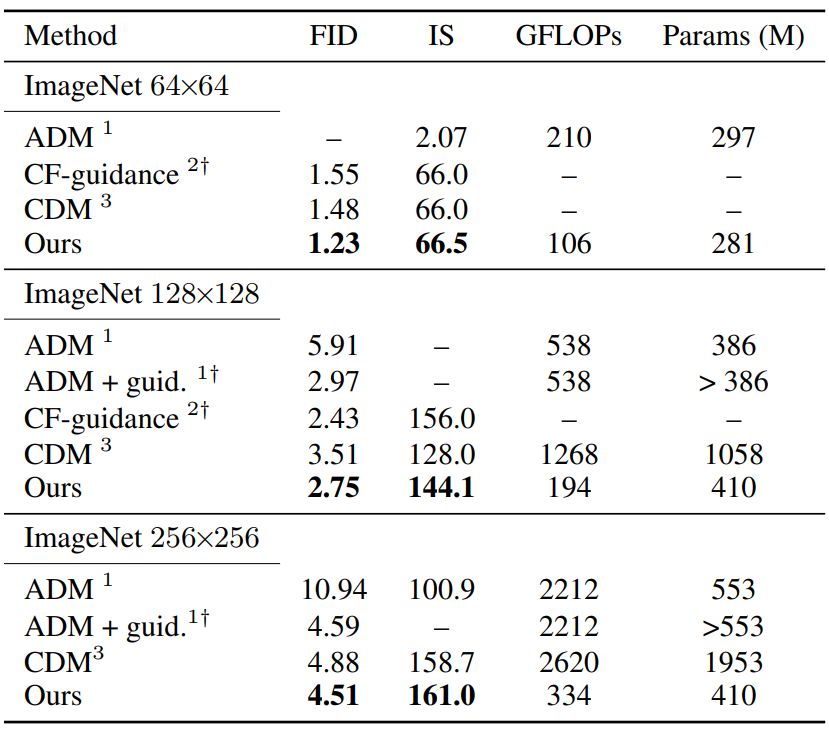
Image Generation

다음은 기존 state-of-the-art diffusion model들과 ImageNet에서 비교한 표이다.

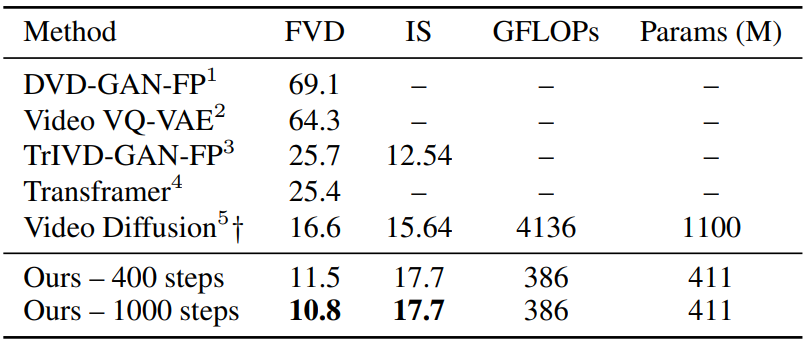
Video Generation

다음은 Kinetics-600 동영상 예측 벤치마크에서 기존 방법들과 본 논문의 모델을 비교한 표이다.

4. Ablations

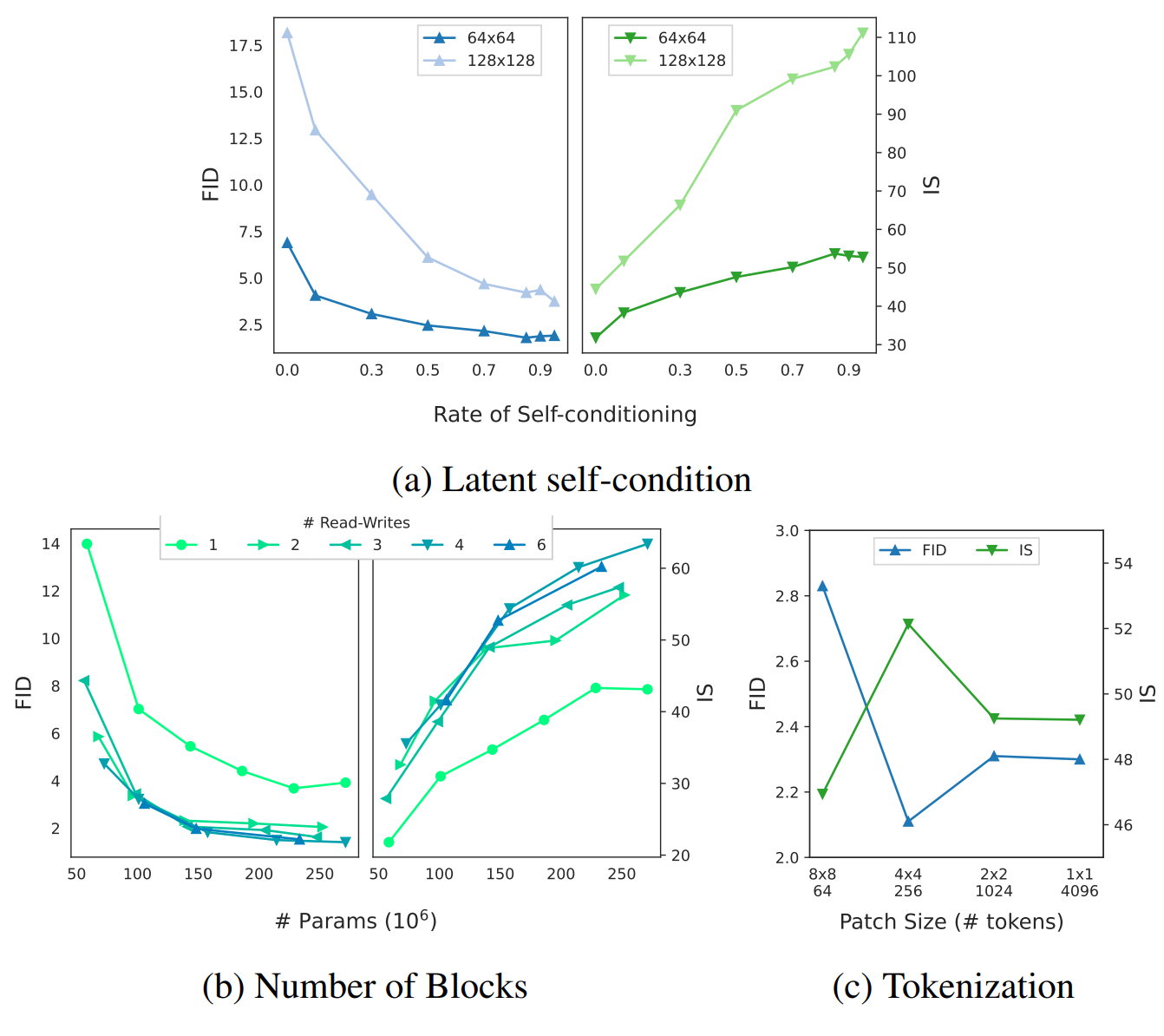
(a)는 학습을 위한 self-conditioning rate의 효과를 나타낸 그래프로, self-conditioning이 중요하다는 것을 볼 수 있다. (b)는 read-write/routing frequency의 효과를 나타낸 그래프로, 여러번의 read-write가 좋은 결과를 얻는 데 중요하다는 것을 알 수 있다. (c)는 토큰화의 효과를 나타낸 그래프로, 모델이 inference에서 많은 토큰을 다룰 수 있음을 보여준다.

다음은 학습과 샘플링에서의 noise schedule의 효과를 나타낸 것이다.

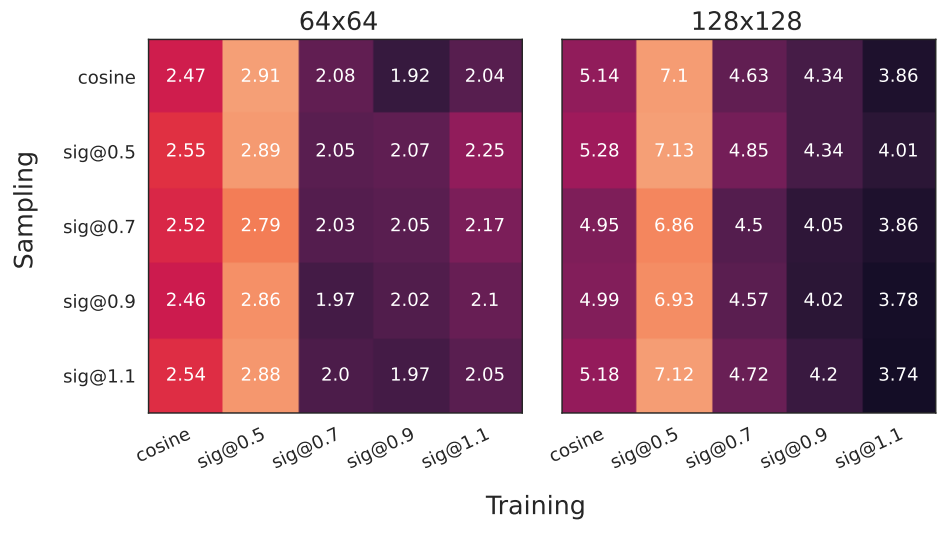
학습 중에 적합한 temperature를 사용한 sigmoid schedule이 cosine schedule보다 좋다는 것을 보여주며, 특히 큰 이미지에서 효과가 크다. 샘플링의 경우 noise schedule의 효과가 크지 않으며 cosine schedule을 사용해도 충분하다.

5. Visualizing Adaptive Computation

네트워크의 긴급 적응 계산을 더 잘 이해하기 위해 읽기 연산의 attention 분포를 시각화하여 정보가 라우팅되는 방식을 분석한다. 이미지 생성의 경우 이는 이미지의 어느 부분이 가장 많이 사용되고 latent 계산이 할당되는 지를 나타낸다.

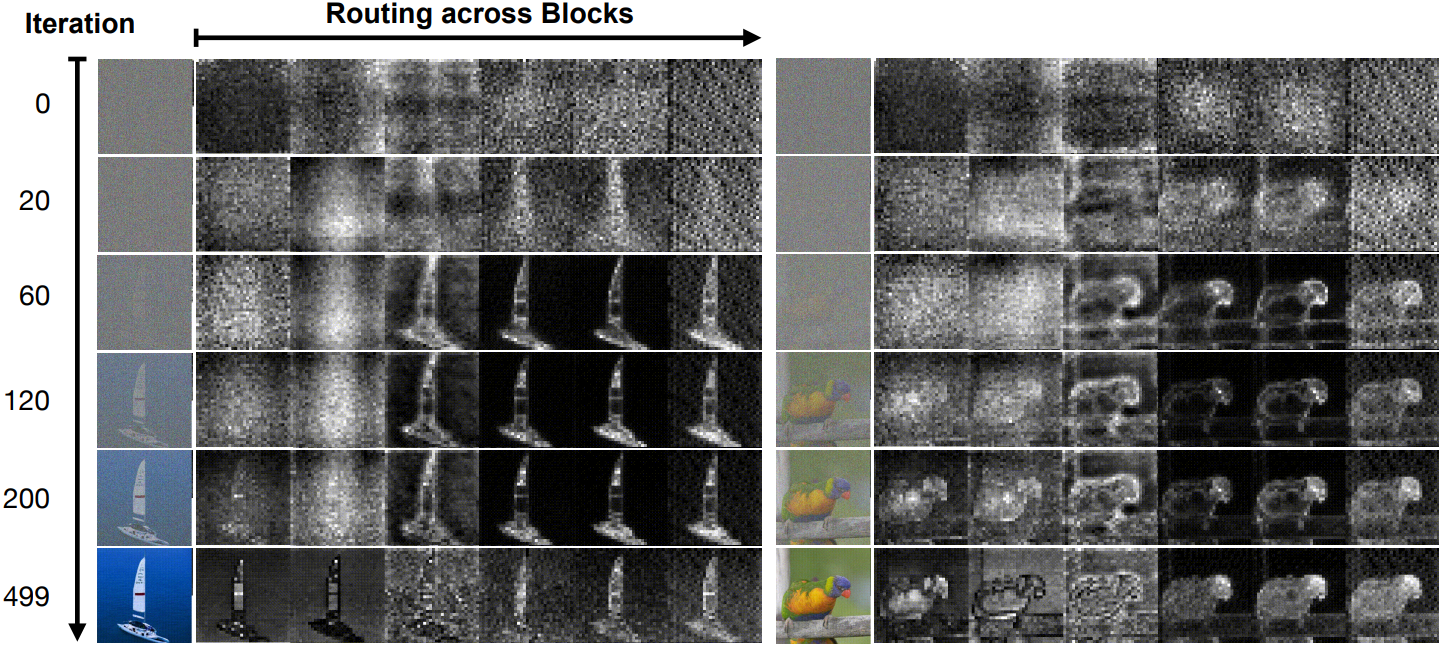
위 그림은 각 forward pass의 block을 통한 read attention (latent에 대한 평균) 뿐만 아니라 reverse process에서 두 샘플의 진행을 보여준다. Reverse process가 진행됨에 따라 초기 읽기 (latent self-conditioning에 의해 guide됨)는 샘플의 정보 밀도에 의해 점점 더 편향된다. 또한, 저자들은 read attention 분포가 정보가 높은 영역을 선호하는 방식으로 더 희박해짐, 즉 낮은 엔트로피가 된다는 것을 발견했다. Read attention은 고용량 계산을 위해 정보를 latent로 로드하기 때문에 모델이 필요에 따라 가장 중요한 정보에 동적으로 계산을 할당하는 방법을 학습한다는 것을 의미한다.