[논문리뷰] Reversible Vision Transformers (Rev-ViT)
CVPR 2022. [Paper] [Github]
Karttikeya Mangalam, Haoqi Fan, Yanghao Li, Chao-Yuan Wu, Bo Xiong, Christoph Feichtenhofer, Jitendra Malik
Meta AI, FAIR | UC Berkeley
9 Feb 2023
Introduction
컴퓨터 비전의 딥 러닝 혁명은 고성능 하드웨어 가속기의 기반 위에 자리잡고 있다. 특수 목적의 AI 가속기에 힘입어 SOTA 모델에 대한 컴퓨팅 요구 사항이 기하급수적으로 증가하고 있다. 그러나 컴퓨팅은 이야기의 절반에 불과하다. 다른 하나는 메모리 대역폭 병목 현상으로, 가속기 FLOPs의 피크와 비교하여 비례적으로 확장하기가 어렵다. 특히, 가속기 FLOPs의 피크는 2년마다 약 3.1배의 비율로 증가하고 있다. 그러나 최대 대역폭은 2년마다 ~1.4배의 비율로만 확장된다. 이러한 차이는 지난 3년 동안 약 3개월마다 필요한 컴퓨팅이 두 배로 증가한 transformer에서 더욱 악화되어 전체 모델 성능과 학습 속도가 모두 메모리에 밀접하게 묶여 있는 소위 memory wall이 발생했다.
따라서 대역폭이 제한된 모델의 경우 재계산을 통해 메모리를 위해 계산을 거래하는 것이 작업 최적화 알고리즘을 사용하는 것보다 실제로 더 효율적일 수 있다. 신경망 모델을 학습하는 경우 activation을 저장한 다음 DRAM에서 로드하는 대신 다시 계산하여 이를 달성할 수 있다. 학습 속도 외에도, 깊이에 대한 ViT 확장은 자연스럽게 GPU 메모리 용량에 영향을 미치며, 특히 SOTA 모델은 중간 activation의 높은 메모리 공간으로 인해 종종 batch size가 1로 제한되는 동영상 인식과 같은 메모리가 부족한 방식에서 더욱 그렇다.
본 논문은 비가역적인 변형들에 비해 매우 유리한 activation 메모리 공간을 갖춘 시각적 인식 아키텍처 클래스인 Reversible Vision Transformer (Rev-ViT)를 제안하였다. 효율적인 즉석 activation 재계산으로 GPU activation 캐싱을 trade-off함으로써 reversible vision transformer는 모델 깊이에서 activation 메모리 증가를 효과적으로 분리한다. NLP 커뮤니티에서는 기계 번역을 위한 reversible transformer에 대한 초기 연구를 수행했지만 이러한 연구들은 깊이보다는 더 긴 시퀀스 길이에 중점을 둔다.
본 논문의 실험은 ViT를 가역 아키텍처에 직접 적용하면 내부 sub-block residual connection으로 인한 학습 수렴 불안정으로 인해 더 깊은 모델에 맞게 확장되지 않음을 보여준다.
본 논문에서는 이 문제를 극복하기 위해 ViT와 MViT의 residual 경로를 재구성하였다. 저자들은 가역적 구조가 더 강력한 고유 정규화를 가지고 있음을 발견했다. 따라서 더 가벼운 augmentation과 residual block 사이의 측면 연결을 사용하였다.
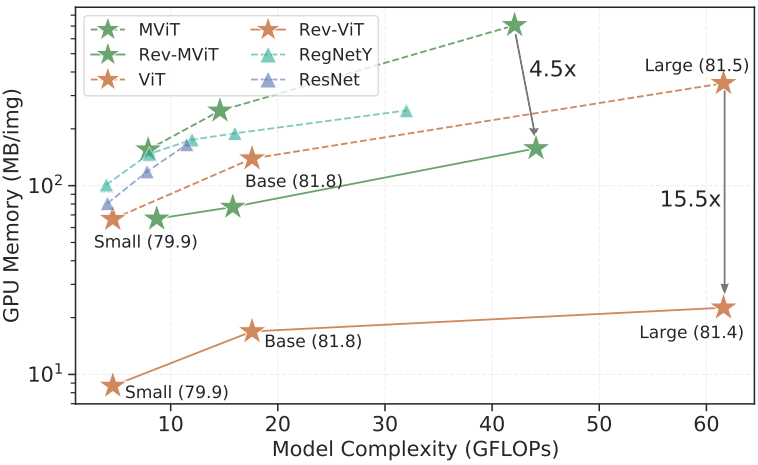
저자들은 이미지 분류, object detection, 동영상 분류와 같은 이미지 인식 task 전반에 걸쳐 광범위하게 벤치마킹하였다. 이 모든 task에서 Rev-ViT는 성능 저하가 무시할 수 있는 비가역적 transformer에 비해 경쟁력 있는 성능을 가지고 있다. 또한 가역 모델은 이미지당 메모리 공간이 매우 유리하여 가역 학습을 통해 ViT-Large 모델에서 15.5배, MViTLarge 모델에서 4.5배를 절약한다.
Approach
1. Reversible Block Structure
Reversible transformer는 출력의 가역성을 허용하기 위해 가역 변환(reversible transformation)의 구조를 따르는 가역 블록의 스택으로 구성된다.
1.1 Reversible Transformation
다음과 같이 임의의 미분가능한 함수 $F(\cdot) : \mathbb{R}^{d} \rightarrow \mathbb{R}^d$를 사용하여 2개의 $d$ 차원 텐서 $[I_1; I_2]$로 분할된 입력 텐서 $I$를 마찬가지로 텐서 $[O_1; O_2]$로 분할된 출력 텐서 $O$로 변환하는 변환 $T_1$을 생각해 보자.
\[\begin{equation} I = \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} \xrightarrow[T_1]{} \begin{bmatrix} O_1 \\ O_2 \end{bmatrix} = \begin{bmatrix} I_1 \\ I_2 + F(I_1) \end{bmatrix} = O \end{equation}\]위의 변환 $T_1$은 $T_1^\prime \circ T_1$이 항등 변환이 되도록 역변환 $T_1^prime$을 허용한다. 또한 다음과 같이 $G(\cdot) : \mathbb{R}^d \rightarrow \mathbb{R}^d$ 함수를 사용하여 유사한 전치 변환 $T_2$를 고려하자.
\[\begin{equation} I = \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} \xrightarrow[T_2]{} \begin{bmatrix} O_1 \\ O_2 \end{bmatrix} = \begin{bmatrix} I_1 + G(I_2) \\ I_2 \end{bmatrix} = O \end{equation}\]$T_1$과 유사하게 $T_2$도 역변환 $T_2^\prime$을 허용한다. 이제 입력 벡터 $I$의 두 파티션을 변환하고 다음과 같이 얻는 $T = T_2 \circ T_1$을 고려하자.
\[\begin{equation} I = \begin{bmatrix} I_1 \\ I_2 \end{bmatrix} \xrightarrow[T]{} \begin{bmatrix} O_1 \\ O_2 \end{bmatrix} = \begin{bmatrix} I_1 + G(I_2 + F(I_1)) \\ I_2 + F(I_1) \end{bmatrix} = O \end{equation}\]당연히 $T$는 $T^\prime (T(I)) = I$를 따르는 역변환 $T^\prime = T_1^\prime \circ T_2^\prime$를 제공한다. 역변환 $T^\prime$은 함수 $F$와 $G$를 정확히 한 번 쿼리하므로 순방향 변환 $T$와 동일한 계산 비용을 갖는다.
1.2 Vanilla networks require caching activations
역전파 메커니즘을 생각해보자. 계산 그래프 노드 $\mathcal{M}$, 해당 하위 노드 \(\{\mathcal{N}_j\}\), 최종 loss에 대한 하위 노드의 기울기 \(\{\frac{d \mathcal{L}}{d \mathcal{N}_j}\}\)가 주어지면 역전파 알고리즘은 chain rule을 사용하여 $\mathcal{M}$에 대한 기울기를 다음과 같이 계산한다.
\[\begin{equation} \frac{d \mathcal{L}}{d \mathcal{M}} = \sum_{\mathcal{N}_j} \bigg( \frac{\partial f_j}{\partial \mathcal{M}} \bigg)^\top \frac{d \mathcal{L}}{d \mathcal{N}_j} \end{equation}\]여기서 $f_j$는 상위 노드 $\mathcal{N}_j$를 계산하는 함수를 나타내며 $\mathcal{M}$은 그 중 하나이다. Jacobian $\frac{\partial f_j}{\partial \mathcal{M}}$은 현재 노드 $\mathcal{M}$에 대한 $f_j$ 출력의 편미분을 계산해야 한다.
이제 가장 간단한 신경망 레이어 $f(X) = W^\top X$를 생각해 보자. 여기서 $X$는 네트워크 내부의 중간 activation이다. 위에서 설명한 역전파 알고리즘을 적용하여 부모 노드에 대한 미분계수를 계산하고 출력 $Y$를 유일한 자식 노드 $\mathcal{N}_j$로 사용하면 다음을 얻는다.
\[\begin{equation} \frac{d \mathcal{L}}{dW} = \bigg( \frac{d \mathcal{L}}{dY} \bigg) X^\top, \quad \frac{d \mathcal{L}}{dX} = W \frac{d \mathcal{L}}{dY} \end{equation}\]따라서 역전파 알고리즘은 가중치에 대한 기울기를 계산하기 위해 backward pass에서 사용할 수 있도록 forward pass의 중간 activation이 필요하다.
일반적으로 이는 backward pass에 사용하기 위해 GPU 메모리에 중간 activation을 캐싱함으로써 달성된다. 이를 통해 추가 메모리 비용으로 빠른 기울기 계산이 가능하다. 또한 네트워크의 순차적 특성으로 인해 loss 기울기가 계산되고 캐싱된 메모리가 해제되기 전에 모든 레이어의 activation이 캐싱되어야 한다. 이러한 의존성은 최대 메모리 사용량에 큰 영향을 미치므로 네트워크 깊이 $D$에 선형 종속이 된다.
1.3 Learning without caching activations
가역 변환 $T$로 변환된 입력을 사용하면 변환 출력에서 입력을 다시 계산할 수 있다. 따라서 이러한 가역적 변환으로 구성된 네트워크는 중간 activation을 저장할 필요가 없다. 출력의 backward pass에서 쉽게 다시 계산할 수 있기 때문이다. 그러나 가역 변환 $T$는 학습된 함수의 속성에 중요한 제약을 둔다.
등차원 제약. 함수 $F$와 $G$는 입력 공간과 출력 공간에서 차원이 같아야 한다. 따라서 feature 차원은 $T$에서 일정하게 유지되어야 한다. 이 제약 조건은 feature 차원의 변경이 필요한 ResNet과 같은 다른 비전 아키텍처에는 방해가 되지만 전체 레이어에서 일정한 feature 차원을 유지하는 ViT 아키텍처에서는 쉽게 충족된다.
2. Reversible Vision Transformers
2.1 Adapting ViT to Two-Residual-Streams
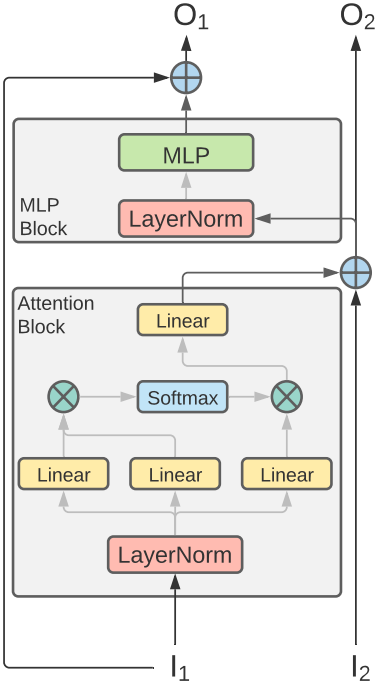
위 그림은 ViT 아키텍처에 적용된 가역 변환 $T$를 보여준다. 입력은 가역성을 유지하면서 변환된 두 개의 분할된 텐서 $I_1$과 $I_2$로 구성된다. 이는 각각의 입력 $I_1$과 $I_2$가 함수 $F$와 $G$를 사용하여 서로 정보를 혼합하면서 자신의 residual 스트림을 유지하는 2개의 residual 스트림 아키텍처로 이어진다. ViT를 따라 Multi-head attention과 MLP sub-block을 각각 함수 $F$와 $G$를 사용한다.
2.2 Boundary Conditions
ViT 아키텍처는 하나의 residual 스트림만 사용하므로 두 개의 residual 스트림 설계를 지원하도록 아키텍처를 수정해야 한다.
- Initiation: Stem을 그대로 유지하고 patchification 출력 activation을 $I_1$과 $I_2$로 보낸다. 이 디자인 선택은 채널 크기를 따라 절반으로 분할하는 RevNet과 다르다.
- Termination: 정보를 보존하려면 최종 classifier head 전에 두 개의 residual 경로를 융합해야 한다. 저자들은 융합 계산 오버헤드를 줄이기 위해 먼저 입력을 layer-normalize한 다음 concatenate하는 것을 제안하였다.
2.3 Reconfiguring Residual Connections
Residual connection은 심층 네트워크에서 신호 전파에 중요한 역할을 한다. 가역 변환 $T$ 자체도 가역성을 유지하기 위해 두 스트림 사이의 residual connection에 의존한다. 흥미롭게도 저자들은 Rev-ViT에서 residual connection과 신호 전파 사이의 주요 관계를 관찰하였다.
더 나은 기울기 흐름을 위해 신경망 블록을 residual block으로 둘러싸는 것이 일반적인 관행이지만 $I_1$ 또는 $I_2$ 입력에는 그러한 연결이 없다. 특히 $I_1$과 $I_2$ 스트림 모두에 대한 MLP와 Attention sub-block 주변의 내부 residual connection이 없다. 대신, 각 residual 스트림에 대한 residual connection은 다른 스트림을 통해 흐르며 가역 변환 $T$에 존재하는 고유한 skip connection을 통해 작동한다. 이러한 내부 skip connection은 더 깊은 모델에 대한 학습 수렴에 해로운 반면 더 얕은 모델에 대해서는 추가 이득을 가져오지 않으며, 저자들은 Rev-ViT 블록에 대해서는 이를 완전히 생략하기로 결정했다.
3. Reversible Multiscale Vision Transformers
최근 제안된 MViT 아키텍처는 시각적 해상도를 다운샘플링하고 채널 차원을 업샘플링하여 모델 내부의 feature 레이어 구조를 개발하였다. MViT는 이미지 및 동영상 분류 벤치마크 모두에서 SOTA 결과를 얻었다. 저자들은 가역 디자인의 유연성을 보여주기 위해 MViT 모델에 이 디자인을 적용했다. Rev-MViT 아키텍처는 MViT 모델과 동일한 구조로 구성되지만 두 개의 서로 다른 레이어인 Stage Transition과 Stage-Preserving 블록을 사용한다.
3.1 Stage-Transition block
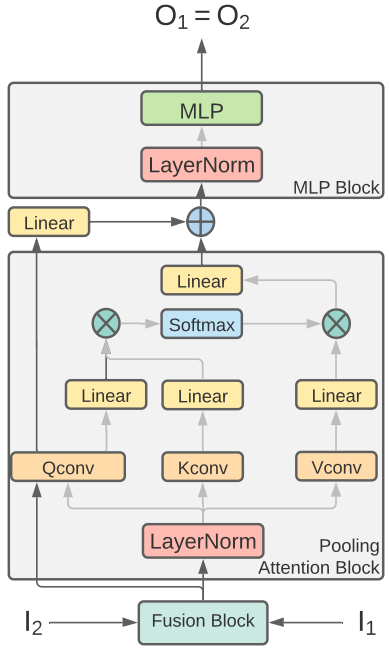
위 그림은 제안된 stage-transition block의 아키텍처를 보여준다. Stage-transition block은 다음과 같은 중요한 수정 사항을 통해 MViT의 해상도 업샘플링 블록 디자인을 밀접하게 따른다.
Lateral Connections. Residual 스트림 $I_1$과 $I_2$는 stage-transition block의 시작 부분에서 측면 연결을 통해 융합된다. 이를 통해 각 스트림에서 별도로 계산을 반복하지 않고도 해상도 다운샘플링과 feature 업샘플링을 효율적으로 계산할 수 있다.
Feature Upsampling. MViT는 해상도 업샘플링 블록 이전의 마지막 MLP 블록에서 feature 업샘플링을 수행한다. 저자들은 stage-transition 블록의 pooling attention sub-block 내에서 채널 업샘플링 단계를 이동할 것을 제안하였다. 구체적으로 풀링 채널별 컨벌루션 레이어 다음의 linear layer에서 query, key, value 벡터를 업샘플링하는 것을 제안하였다. 이는 다음과 같은 2가지 이점이 있다.
- 모든 feature 차원 변경이 동일한 블록 내에서 동기화되도록 허용하고 다른 블록이 feature 차원을 그대로 유지하도록 허용
- MLP와 풀링 레이어에서 추가 비용 절감
Rev-ViT 아키텍처에서와 같이 stage-transition block에서는 동일한 경계 조건을 따른다.
3.2 Stage-Preserving Block
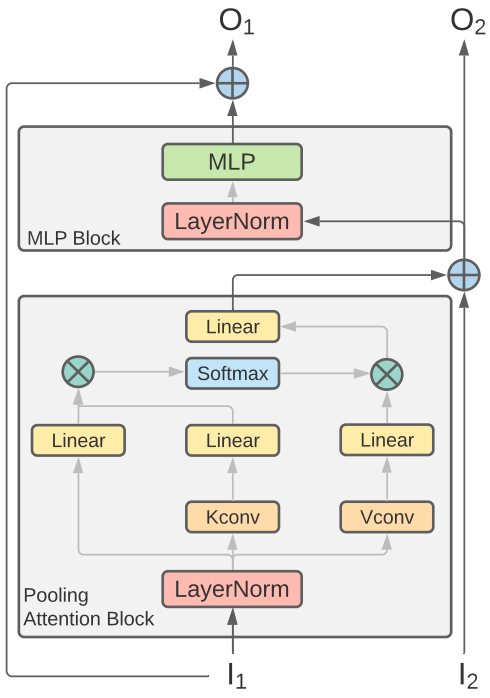
위 그림은 MViT 아키텍처에 적용된 가역 변환 $T$를 보여준다. 디자인은 multi-head pooling attention이 추가된 Rev-ViT 블록의 디자인과 매우 유사하다. Attention이 key와 value 텐서에 대한 pooling을 사용하여 시퀀스 길이를 변경하더라도 출력 차원은 여전히 유지된다. 따라서 stage-preserving block은 여전히 등차원 제약 조건을 따르므로 완전히 가역적이고 activation 캐싱 없이 학습될 수 있다.
각 stage-transition block은 시공간 해상도를 변경하므로 전체 MViT 네트워크에서 제한된 횟수만 발생한다. 즉, 대부분의 계산과 메모리 사용량이 stage-preserving block 내에서 수행되며 완전히 가역적이다. Stage-transition block과 stage-preserving block 모두에 대해 Rev-ViT 블록에서와 동일한 residual connection 회로를 따른다.
Results
- 데이터셋
- 이미지 분류: ImageNet-1K
- 동영상 분류: Kinetics 400, Kinetics 600
- Object detection: MS-COCO
1. Image Classification
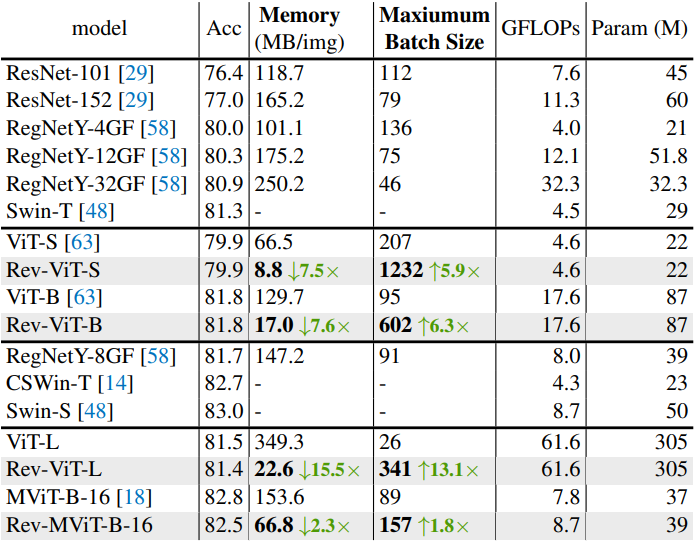
다음은 ImageNet-1K 분류에 대하여 이전 방법들과 비교한 표이다.
2. Video Classification
다음은 Kinetics-400 동영상 분류에 대하여 이전 방법들과 비교한 표이다.
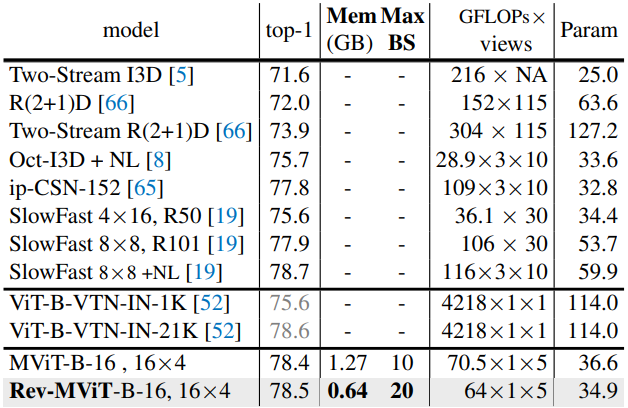
다음은 Kinetics-600 동영상 분류에 대하여 이전 방법들과 비교한 표이다.
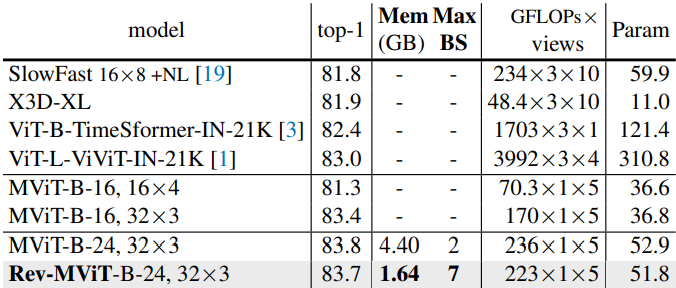
3. Object Detection
다음은 MS-COCO object detection에 대하여 이전 방법들과 비교한 표이다.
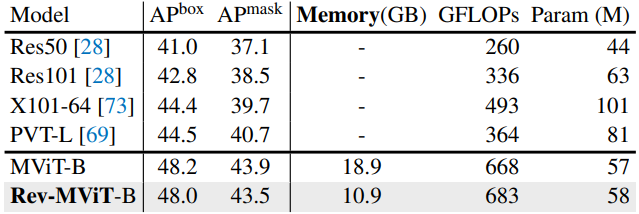
4. Ablations
다음은 Rev-ViT-B 학습에 대한 ablation 결과이다.

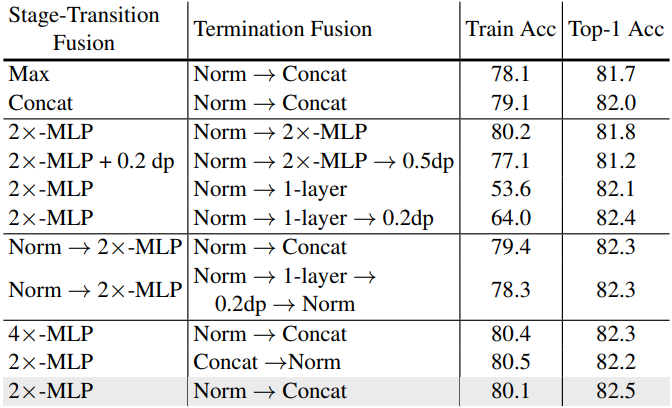
다음은 측면 융합 전략에 대한 ablation 결과이다.
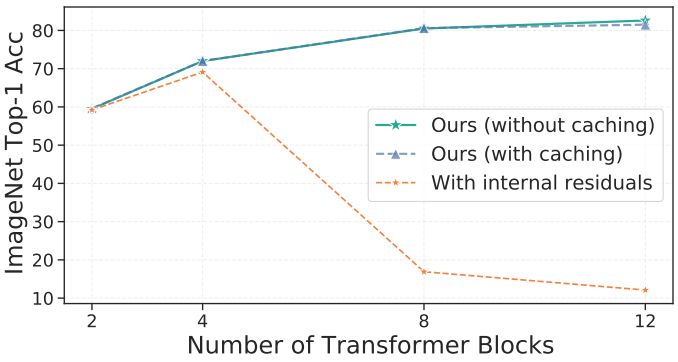
다음은 activation 캐싱과 내부 residual에 대한 ablation 결과이다.
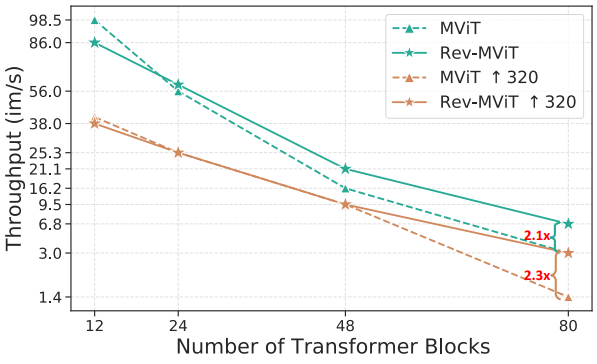
다음은 모델 크기와 입력 해상도에 대한 이미지 처리량(throughput)을 비교한 그래프이다.
다음은 최대 batch size 크기를 비교한 그래프이다.