Diffusion은 신이고 GPT는 무적이다

arXiv 2023. [Paper] [Github]
Yutao Sun, Li Dong, Shaohan Huang, Shuming Ma, Yuqing Xia, Jilong Xue, Jianyong Wang, Furu Wei
Microsoft Research | Tsinghua University
17 Jul 2023

Introduction

Transformer는 처음에 recurrent model의 순차 학습 문제를 극복하기 위해 제안된 사실상의 대규모 언어 모델을 위한 아키텍처가 되었다. 그러나 Transformer의 학습 병렬화는 step당 $O(N)$ 복잡도와 메모리 바인딩된 key-value 캐시로 인해 Transformer를 배포하기 어렵게 만들기 때문에 비효율적인 inference의 대가를 치르게 된다. 시퀀스 길이가 늘어나면 GPU 메모리 소비와 대기 시간이 증가하고 inference 속도가 감소한다.


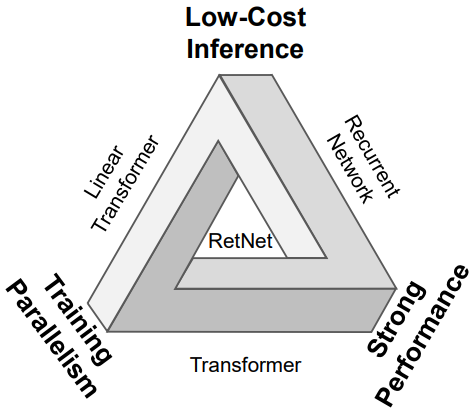
효율적인 $O(1)$ inference를 갖는 동시에 Transformer로서 학습 병렬성과 경쟁력 있는 성능을 유지하는 것을 목표로 차세대 아키텍처를 개발하기 위한 수많은 노력이 계속되었다. 위의 목표, 즉 위 그림의 소위 “불가능한 삼각형”을 동시에 달성하는 것은 어렵다.

연구에는 세 가지 주요 방향이 있었다. 첫째, 선형화된 attention은 표준 attention 점수 $\exp(q \cdot k)$를 커널 $\phi(q) \cdot \phi (k)$로 근사화하므로 autoregressive inference이 반복 형식으로 다시 쓸 수 있다. 그러나 Transformer에 비해 모델링 능력과 성능이 좋지 않아 대중화에 걸림돌이 되고 있다. 두 번째 가닥은 학습 병렬성을 희생하면서 효율적인 inference를 위해 recurrent model로 돌아가는 것이다. 이에 대한 해결책으로 가속을 위해 element-wise 연산자를 사용하지만 표현 능력과 성능이 저하된다. 세 번째 연구 라인에서는 attention을 S4와 같은 다른 메커니즘으로 대체하는 방법을 탐구한다. 이전 연구들 중 그 어느 것도 불가능한 삼각형을 돌파하지 못해 Transformer를 뛰어넘는 확실한 승자가 나오지 않았다.

본 논문에서는 저비용 inference, 효율적인 긴 시퀀스 모델링, Transformer와 비교할 수 있는 성능, 병렬 모델 학습을 동시에 달성하는 Retentive Network (RetNet)을 제안하였다. 구체적으로, multi-head attention을 대체하기 위하여 세 가지 계산 패러다임, 즉 병렬 표현, 순환 표현, 청크별 순환 표현을 갖는 멀티스케일 retention 메커니즘을 도입한다.

  1. 병렬 표현은 GPU 장치를 완전히 활용할 수 있도록 학습 병렬성을 강화한다.
  2. Recurrent 표현은 메모리와 계산 측면에서 효율적인 $O(1)$ inference를 가능하게 한다. 배포 비용과 대기 시간을 크게 줄일 수 있다. 게다가 키-값 캐시 트릭 없이 구현이 크게 단순화되었다.
  3. 청크별 순환 표현은 효율적인 긴 시퀀스 모델링을 수행할 수 있다. 계산 속도를 위해 각 로컬 블록을 병렬로 인코딩하는 동시에 GPU 메모리를 절약하기 위해 글로벌 블록을 반복적으로 인코딩한다.

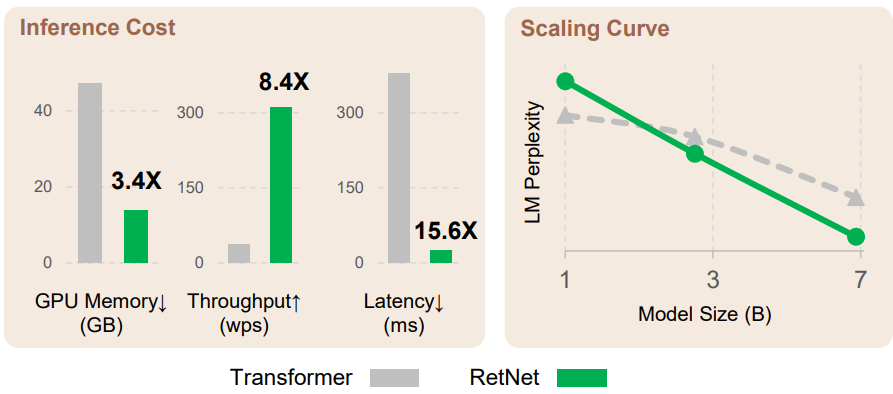
저자들은 RetNet을 Transformer 및 그 변형들과 비교하기 위해 광범위한 실험을 수행하였다. 언어 모델링에 대한 실험 결과는 RetNet이 스케일링 곡선과 in-context learning 측면에서 지속적으로 경쟁력이 있음을 보여준다. 게다가 RetNet의 inference 비용은 길이에 따라 변하지 않는다. 7B 모델과 8k 시퀀스 길이의 경우 RetNet은 key-value 캐시를 사용하는 Transformer보다 8.4배 더 빠르게 디코딩하고 70%의 메모리를 절약한다. 또한 학습 중에 RetNet은 표준 Transformer보다 25~50%의 메모리 절약과 7배의 가속을 달성하며 고도로 최적화된 FlashAttention에 대한 이점을 제공한다. 게다가 RetNet의 inference 대기 시간은 batch size에 민감하지 않으므로 엄청난 처리량을 허용한다. 흥미로운 속성들로 인해 RetNet은 대규모 언어 모델을 위한 Transformer의 강력한 후계자가 되었다.

Retentive Networks

Retentive network (RetNet)는 Transformer와 유사한 레이아웃 (즉, residual connection, pre-LayerNorm)을 따르는 $L$개의 동일한 블록으로 쌓인다. 각 RetNet 블록에는 multi-scale retention (MSR) 모듈과 feed-forward network (FFN) 모듈이라는 두 개의 모듈이 포함되어 있다.

입력 시퀀스 $x = x_1 \cdots x_{\vert x \vert}$가 주어지면, RetNet은 autoregressive 방식으로 시퀀스를 인코딩한다. 입력 벡터 \(\{x_i\}_{i=1}^{\vert x \vert}\)은 먼저 \(X^0 = [x_1, \cdots, x_{\vert x \vert}] \in \mathbb{R}^{\vert x \vert \times d_\textrm{model}}\)로 압축된다. 여기서 $d_\textrm{model}$은 hidden 차원이다. 그런 다음 컨텍스트화된 벡터 표현 $X^l = \textrm{RetNet}_l (X^{l-1}), l \in [1, L]$을 계산한다.

1. Retention

본 논문은 반복과 병렬의 이중 형태를 갖는 retention 메커니즘을 도입하였다. 따라서 반복적으로 추론을 수행하면서 병렬 방식으로 모델을 학습시킬 수 있다.

입력 $X \in \mathbb{R}^{\vert x \vert \times d_\textrm{model}}$이 주어지면 이를 1차원 함수 $v(n) = X_n \cdot w_V$로 project한다. 상태 $s_n$을 통해 $v(n) \mapsto o(n)$을 매핑하는 시퀀스 모델링 문제를 생각해 보자. 단순화를 위해 $v(n)$, $o(n)$을 $v_n$, $o_n$으로 표시하자. 다음과 같이 반복적인 방식으로 매핑을 공식화한다.

\[\begin{aligned} s_n &= As_{n-1} + K_n^\top v_n, \quad A \in \mathbb{R}^{d \times d}, K_n \in \mathbb{R}^{1 \times d} \\ o_n &= Q_n s_n = \sum_{m=1}^n Q_n A^{n-m} K_m^\top v_m, \quad Q_n \in \mathbb{R}^{1 \times d} \end{aligned}\]

여기서 $v_n$을 상태 벡터 $s_n$에 매핑한 다음 선형 변환을 구현하여 시퀀스 정보를 반복적으로 인코딩한다.

다음으로 projection $Q_n$, $K_n$가 컨텐츠를 인식하도록 만든다.

\[\begin{equation} Q = XW_Q, \quad K = XW_K \end{equation}\]

여기서 $W_Q, W_K \in \mathbb{R}^{d \times d}$는 학습 가능한 행렬이다.

행렬 $A$를 대각화한다.

\[\begin{equation} A = \Lambda (\gamma e^{i \theta}) \Lambda^{-1}, \quad \textrm{where} \; \gamma, \theta \in \mathbb{R}^d \end{equation}\]

그런 다음 \(A = \Lambda (\gamma e^{i \theta})^{n-m} \Lambda^{-1}\)을 얻는다. $\Lambda$를 $W_Q$와 $W_K$에 흡수함으로써 매핑 식을 다음과 같이 다시 쓸 수 있다.

\[\begin{aligned} o_n &= \sum_{m=1}^n Q_n (\gamma e^{i \theta})^{n-m} K_m^\top v_m \\ &= \sum_{m=1}^n (Q_n (\gamma e^{i \theta})^n) (K_m (\gamma e^{i \theta})^{-m})^\top v_m \end{aligned}\]

여기서 $Q_n (\gamma e^{i \theta})^n$, $K_m (\gamma e^{i \theta})^{-m}$는 xPos로 알려져 있다. 즉, Transformer를 위해 제안된 상대 위치 임베딩이다. $\gamma$를 스칼라로 더욱 단순화하면 위 식은 다음과 같다.

\[\begin{equation} o_n = \sum_{m=1}^n \gamma^{n-m} (Q_n e^{in \theta})(K_m e^{im \theta})^\dagger v_m \end{equation}\]

여기서 $\vphantom{1}^{\dagger}$는 켤레 전치 (conjugate transpose)이다. 위 공식을 학습 인스턴스 내에서 쉽게 병렬화할 수 있다.

The Parallel Representation of Retention


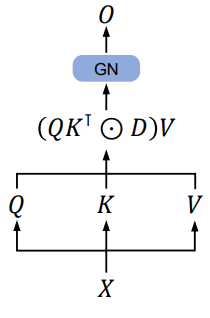
위 그림에 표시된 것처럼 retention layer는 다음과 같이 정의된다.

\[\begin{equation} Q = (XW_Q) \odot \Theta, \quad K = (XW_K) \odot \bar{\Theta}, \quad V = XW_V \\ \Theta_n = e^{in \theta}, \quad D_{nm} = \begin{cases} \gamma^{n-m}, & n \ge m \\ 0, & n < m \end{cases} \\ \textrm{Retention}(X) = (QK^\top \odot D) V \end{equation}\]

여기서 $\bar{\Theta}$는 $\Theta$의 켤레 복소수이고 $D \in \mathbb{R}^{\vert x \vert \times \vert x \vert}$는 인과 마스킹 (causal masking)과 상대 거리에 따른 exponential decay를 하나의 행렬로 결합한다. Self-attention과 유사하게 병렬 표현을 사용하면 GPU를 사용하여 모델을 효율적으로 학습시킬 수 있다.

The Recurrent Representation of Retention


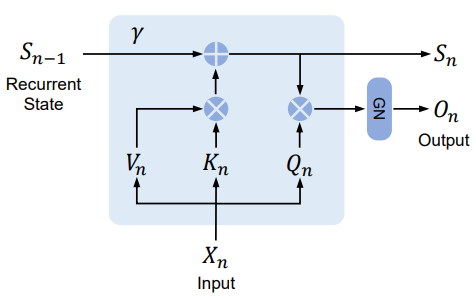
위 그림에서 볼 수 있듯이 제안된 메커니즘은 inference에 유리한 RNN으로 쓸 수도 있다. $n$번째 timestep에 대해 다음과 같이 출력을 반복적으로 얻는다.

\[\begin{aligned} & S_n = \gamma S_{n-1} + K_n^\top V_n \\ & \textrm{Retention}(X_n) = Q_n S_n, \quad n = 1, \cdots, \vert x \vert \end{aligned}\]

The Chunkwise Recurrent Representation of Retention

특히 긴 시퀀스의 경우 학습 속도를 높이기 위해 병렬 표현과 순환 표현의 하이브리드 형태를 사용할 수 있다. 입력 시퀀스를 청크로 나눈다. 각 청크 내에서 병렬 표현을 따라 계산을 수행한다. 대조적으로, 청크 사이의 정보는 순환 표현에 따라 전달된다. $B$를 청크 길이하고 하면, 다음 식을 통해 $i$번째 청크의 retention 출력을 계산한다.

\[\begin{equation} Q_{[i]} = Q_{Bi:B(i+1)}, \quad K_{[i]} = K_{Bi:B(i+1)}, \quad V_{[i]} = V_{Bi:B(i+1)} \\ R_i = K_{[i]}^\top (V_{[i]} \odot \zeta) + \gamma^B R_{i-1}, \quad \zeta_{ij} = \gamma^{B-i-1} \\ \textrm{Retention}(X_{[i]}) = (Q_{[i]} K_{[i]}^\top \odot D) V_{[i]} + (Q_{[i]} R_{i-1}) \odot \xi, \quad \xi_{ij} = \gamma^{i+1} \end{equation}\]

여기서 $[i]$는 $i$번째 청크를 나타낸다. 즉, $x_{[i]} = [x_{(i-1)B+1}, \cdots, x_{iB}]$이다.

2. Gated Multi-Scale Retention

각 레이어에 $h = d_\textrm{model} / d$개의 고정 head를 사용한다. 여기서 $d$는 head 차원이다. Head는 서로 다른 파라미터 행렬 $W_Q, W_K, W_V \in \mathbb{R}^{d \times d}$를 사용한다. 또한 multi-scale retention (MSR)은 각 head에 대해 서로 다른 $\gamma$를 할당한다. 단순화를 위해 서로 다른 레이어 간에 $\gamma$를 동일하게 설정하고 고정된 상태로 유지한다. 또한, retention layer의 비선형성을 높이기 위해 swish gate를 추가했다. 입력 $X$가 주어지면 레이어를 다음과 같이 정의한다.

\[\begin{aligned} \gamma &= 1 - 2^{-5-\textrm{arange}(0, h)} \in \mathbb{R}^h \\ \textrm{head}_i &= \textrm{Retention} (X, \gamma_i) \\ Y &= \textrm{GroupNorm}_h (\textrm{Concat} (\textrm{head}_1, \cdots, \textrm{head}_h)) \\ \textrm{MSR} (X) &= (\textrm{swish}(XW_G) \odot Y) W_O \end{aligned}\]

여기서 $W_G, W_O \in \mathbb{R}^{d_\textrm{model} \times d_\textrm{model}}$은 학습 가능한 파라미터이고 GroupNorm은 각 head의 출력을 정규화한다.

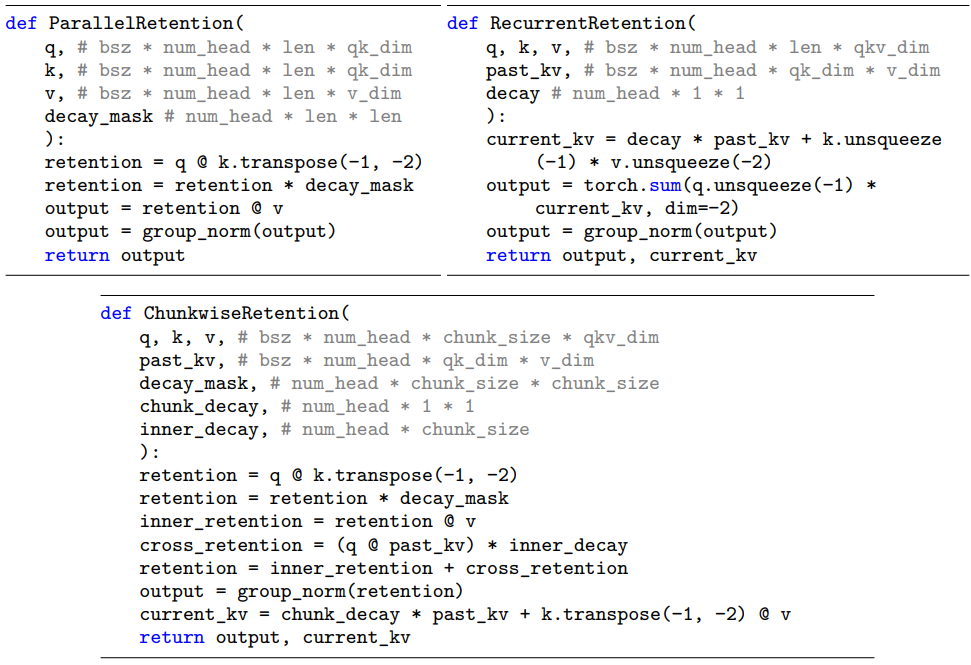
Retention의 pseudocode는 아래 그림에 요약되어 있다.

Retention Score Normalization

GroupNorm의 스케일 불변 특성을 활용하여 retention 레이어의 수치적 정밀도를 향상시킨다. 특히, GroupNorm 내에서 스칼라 값을 곱하여도 출력과 역방향 기울기에 영향을 주지 않는다.

\[\begin{equation} \textrm{GroupNorm}(\alpha \ast \textrm{head}_i) = \textrm{GroupNorm}(\textrm{head}_i) \end{equation}\]

저자들은 세 가지 정규화 요소를 구현하였다.

\[\begin{aligned} QK^\top &\rightarrow \frac{QK^\top}{\sqrt{d}} \\ D &\rightarrow \tilde{D}_{nm} = \frac{D_{nm}}{\sqrt{\sum_{i=1}^n D_{ni}}} \\ R = QK^\top \odot D &\rightarrow \tilde{R}_{nm} = \frac{R_{nm}}{\max (\vert \sum_{i=1}^n R_{ni} \vert, 1)} \end{aligned}\]

그러면 retention 출력은 $\textrm{Retention}(X) = \tilde{R} V$가 된다. 위의 트릭은 스케일 불변 속성으로 인해 forward pass와 backward pass 모두의 수치적 흐름을 안정화하면서 최종 결과에 영향을 미치지 않는다.

3. Overall Architecture of Retention Networks

$L$ 레이어 retention network의 경우 multi-scale retention (MSR)과 feed-forward network (FFN)을 쌓아 모델을 구축한다. 입력 시퀀스 \(\{x_i\}_{i=1}^{\vert x \vert}\)는 단어 임베딩 레이어를 통해 벡터로 변환된다. 압축된 임베딩 $X^0 = [x_1, \cdots, x_{\vert x \vert}] \in \mathbb{R}^{\vert x \vert \times d_\textrm{model}}$을 입력으로 사용하고 모델 출력 $X^L$을 계산한다.

\[\begin{aligned} Y^l &= \textrm{MSR} (\textrm{LN} (X^l)) + X^l \\ X^{l+1} &= \textrm{FFN} (\textrm{LN} (Y^l)) + Y^l \end{aligned}\]

여기서 $\textrm{LN}(\cdot)$은 LayerNorm이다. FFN 부분은 $\textrm{FFN}(X) = \textrm{gelu}(XW_1)W_2$로 계산된다. 여기서 $W_1$, $W_2$는 파라미터 행렬이다.

Training

학습 과정에서 병렬 표현과 청크별 순환 표현을 사용한다. 시퀀스 또는 청크 내의 병렬화는 GPU를 효율적으로 활용하여 계산을 가속화한다. 더 좋은 점은 청크별 순환 표현이 특히 긴 시퀀스 학습에 유용하다는 것이다. 이는 FLOPs와 메모리 소비 측면에서 모두 효율적이다.

Inference

순환 표현은 inference 중에 사용되며, 이는 autoregressive 디코딩에 잘 맞는다. $O(1)$ 복잡도는 동일한 결과를 얻으면서 메모리 및 inference 지연 시간을 줄인다.

4. Relation to and Differences from Previous Methods


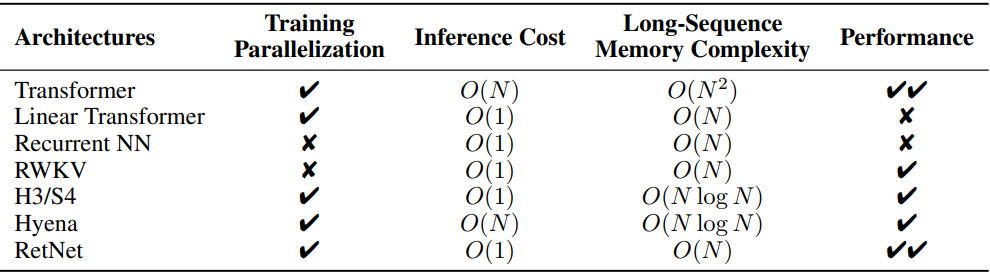
위 표는 RetNet을 다양한 관점에서 이전 방법들과 비교한 것이다. 비교 결과는 “불가능한 삼각형”을 반영한다. 또한 RetNet은 청크별 순환 표현으로 인해 긴 시퀀스에 대해 선형 메모리 복잡도를 갖는다.

Experiments

  • 데이터셋: Pile, C4, The Stack
  • 구현 디테일
    • batch size: 400만 토큰 (최대 길이 2048)
    • step 수: 25만 (1000억 토큰)
    • optimizer: AdamW ($\beta_1$ = 0.9, $\beta_2$ = 0.98, weight decay = 0.05)
    • warmup step: 375 (linear decay)
    • 학습 안정성을 위해 DeepNet을 따라 파라미터 초기화
    • 512개의 AMD MI200 GPU에서 학습

다음은 언어 모델링 실험에서 사용한 모델의 크기와 학습 hyperparameter이다.

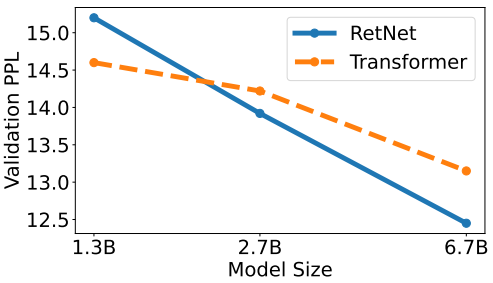
1. Comparisons with Transformer

다음은 모델 크기에 따른 perplexity (PPL)를 비교한 그래프이다.


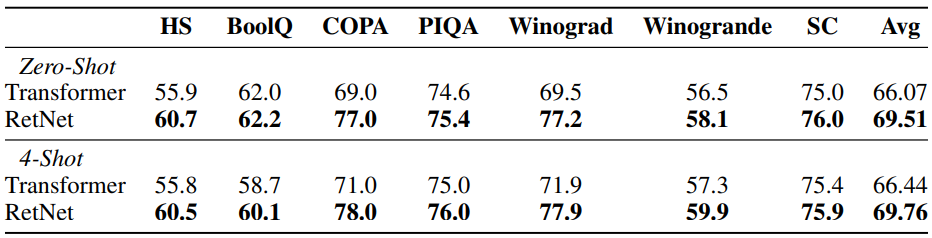
다음은 Transformer와 RetNet의 zero-shot 및 few-shot 성능 비교한 표이다.

2. Training Cost

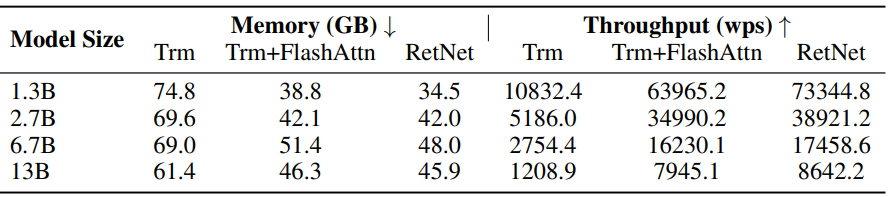
다음은 Transformer (Trm), FlashAttention을 사용한 Transformer (Trm+FlashAttn), RetNet의 학습 비용을 비교한 표이다. (wps: 초당 단어 처리량)

3. Inference Cost

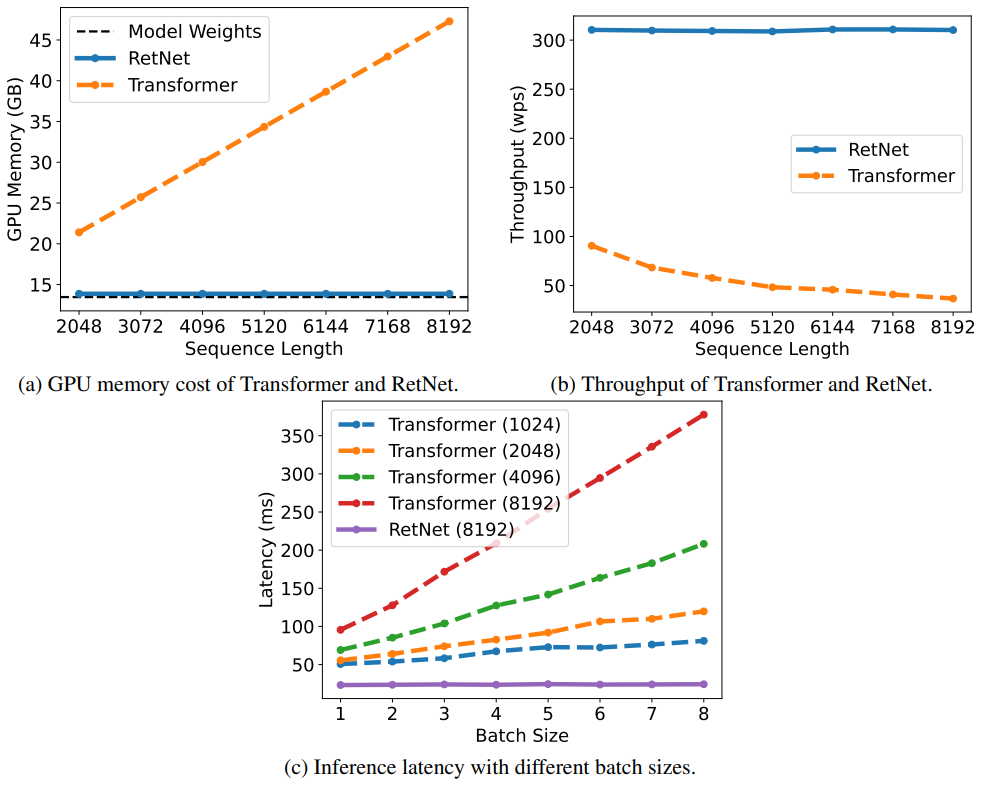
다음은 Transformer와 RetNet의 inference를 비교한 그래프이다.

4. Comparison with Transformer Variants

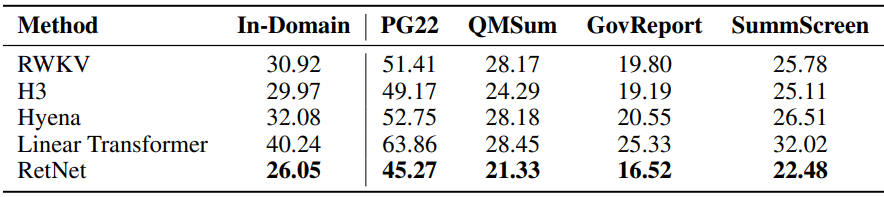
다음은 언어 모델링에 대한 perplexity를 다양한 방법들과 비교한 표이다.

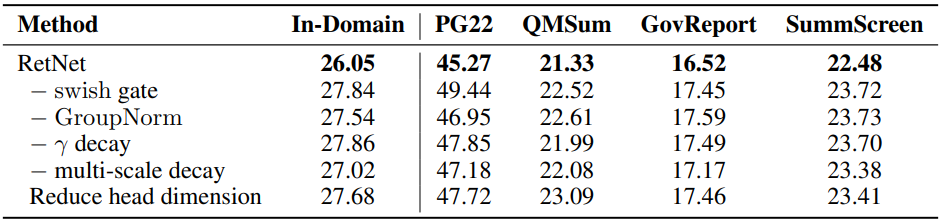
5. Ablation Studies

다음은 ablation study 결과이다.

You may also enjoy