[논문리뷰] Representation Alignment for Generation: Training Diffusion Transformers Is Easier Than You Think

ICLR 2025 (Oral). [Paper] [Page] [Github]
Sihyun Yu, Sangkyung Kwak, Huiwon Jang, Jongheon Jeong, Jonathan Huang, Jinwoo Shin, Saining Xie
KAIST | Korea University | Scaled Foundations | New York University
9 Oct 2024

Introduction

본 논문에서는 diffusion model 학습의 주요 과제가 고품질의 내부 표현 $\textbf{h}$를 학습해야 한다는 필요성에서 비롯된다는 점을 밝힌다. 또한 저자들은 외부 표현 \(\textbf{y}_\ast\)의 지원을 받을 때 diffusion model의 학습 과정이 훨씬 더 쉽고 효율적으로 개선됨을 보여준다. 구체적으로, \(\textbf{y}_\ast\)로 활용되는 self-supervised learning 기반 시각적 표현을 활용한 간단한 정규화 기법을 제안하여 DiT의 학습 효율성과 생성 품질을 크게 향상시켰다.

본 논문에서는 SiT 모델과 DINOv2를 사용하여 분석을 수행하였다. 이전 연구들과 유사하게, 먼저 사전 학습된 diffusion model이 의미 있는 표현을 학습한다는 것을 먼저 확인했다. 그러나 이러한 표현은 DINOv2가 생성한 표현보다 현저히 떨어진다. 또한, diffusion model이 학습한 표현과 DINOv2의 표현 간의 정렬이 여전히 미흡하다는 것을 발견했다. 이를 확인하기 위해 표현 정렬을 측정했다. 마지막으로, diffusion model과 DINOv2 간의 정렬이 학습 시간이 길어지고 모델 크기가 커질수록 지속적으로 향상되는 것을 관찰했다.

이러한 통찰력은 외부 self-supervised 표현을 통합하여 생성 모델을 개선하는 데 영감을 주었다. 그러나 self-supervised 비전 인코더를 사용할 때 이 접근 방식은 간단하지 않다. 첫 번째 문제는 입력 불일치이다. Diffusion model은 noise가 포함된 입력 \(\tilde{\textbf{x}}\)을 사용하는 반면, 대부분의 self-supervised 인코더는 깨끗한 이미지 $\textbf{x}$로 학습된다. 이 문제는 사전 학습된 VAE 인코더에서 압축된 latent 이미지 $\textbf{z} = E(\textbf{x})$를 입력으로 사용하는 latent diffusion model에서 더욱 두드러진다. 또한, 비전 인코더는 재구성이나 생성과 같은 task를 위해 설계되지 않았다. 따라서 저자들은 사전 학습된 self-supervised 표현을 diffusion 표현으로 distillation하는 정규화 기법을 사용하여 diffusion model의 feature 학습을 유도함으로써 고품질 표현을 유연하게 통합하는 방법을 제시하였다.

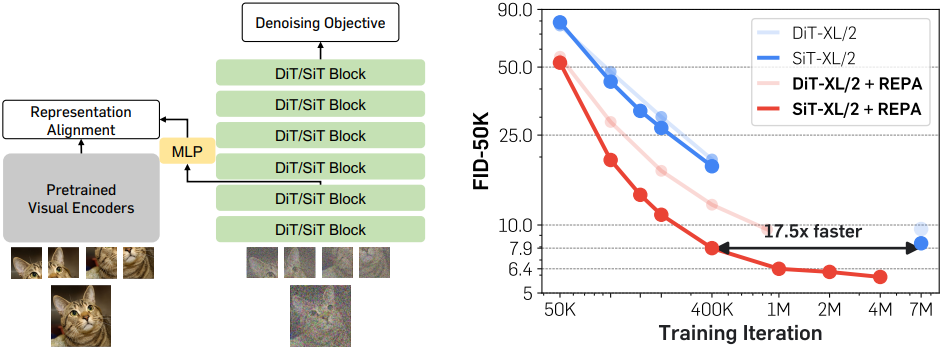
구체적으로, 본 논문에서는 DiT 아키텍처를 기반으로 구축된 간단한 정규화 기법인 REPresentation Alignment (REPA)를 소개한다. REPA는 깨끗한 이미지 $\textbf{x}$의 사전 학습된 self-supervised 표현 \(\textbf{y}_\ast\)를 noise가 포함된 입력 이미지 \(\tilde{\textbf{x}}\)의 DiT 표현 $\textbf{h}$로 distillation한다. 이 정규화는 표현 $\textbf{h}$의 semantic 간극을 줄이고 목표 self-supervised 표현 \(\textbf{y}_\ast\)와 더 잘 정렬되도록 한다. 특히, 이러한 향상된 정렬은 DiT의 생성 성능을 크게 향상시킨다. 흥미롭게도, REPA를 사용하면 처음 몇 개의 DiT block만 정렬해도 충분한 표현 정렬을 달성할 수 있다. 결과적으로, DiT의 후반 layer는 정렬된 표현을 기반으로 고주파 디테일을 포착하는 데 집중할 수 있어 생성 성능이 더욱 향상된다.

SiT의 경우, 클래스 조건부 ImageNet 생성에서 단 40만 iteration만으로 FID 7.9를 달성했는데, 이는 기존 SiT보다 17.5배 이상 빠른 결과이다. 또한, classifier-free guidance (CFG)를 적용했을 때, 최종 FID를 2.06에서 1.80으로 향상시키고, guidance interval을 적용했을 때 FID 1.42라는 SOTA 결과를 달성했다.

Method

1. Overview

데이터 $\textbf{x} \in \mathcal{X}$에 대한 목표 분포를 $p(\textbf{x})$라고 하자. 본 논문의 목표는 $p(\textbf{x})$에서 추출한 데이터셋을 사용하여 모델 분포를 통해 $p(\textbf{x})$를 근사하는 것이다. 계산 비용을 줄이기 위해 latent diffusion 기법을 채택하였으며, $\textbf{x}$는 사전 학습된 VAE의 인코더를 사용하여 \(\textbf{z} = E(\textbf{x})\)로 압축된다.

본 논문에서는 $\textbf{v}$-prediction과 같은 loss를 사용하여 diffusion model \(\textbf{v}_\theta (\textbf{z}_t, t)\)를 학습함으로써 이러한 분포를 학습하고자 한다. 여기서 저자들은 self-supervised 표현 학습의 맥락에서 denoising score matching을 다시 살펴보았다. 이러한 관점에서 diffusion model은 인코더 \(f_\theta (\textbf{z}_t) = \textbf{h}_t\)와 디코더 \(g_\theta (\textbf{h}_t) = \textbf{v}_t\)의 합성으로 생각할 수 있으며, 인코더 \(f_\theta\)는 타겟 \(\textbf{v}_t\)를 재구성하는 표현 \(\textbf{h}_t\)를 암시적으로 학습한다.

그러나 입력 공간을 예측하여 좋은 표현을 학습하는 것은 어려운 과제이다. 모델이 불필요한 디테일을 제거하는 데 어려움을 겪는 경우가 많기 때문이다. 이는 강력한 표현을 개발하는 데 매우 중요하다. 본 논문에서는 대규모 diffusion model 학습의 핵심 한계점이 표현 학습에 있다고 주장한다. 또한, diffusion model이 시각적 표현을 독립적으로 학습하는 데만 의존하는 대신, 고품질의 외부 시각적 표현을 모델에 제공함으로써 학습 과정을 간소화할 수 있다는 가설을 제시하였다.

이러한 문제를 해결하기 위해, 저자들은 DiT 아키텍처를 활용한 REPresentation Alignment (REPA)라는 간단한 정규화 방법을 제안하였다. 이 정규화 방법은 사전 학습된 self-supervised 기반 시각적 표현을 DiT로 간단하고 효과적으로 distillation한다. 이를 통해 diffusion model은 풍부한 외부 semantic 표현을 생성에 활용할 수 있게 되어 성능이 크게 향상된다.

2. Observations

이를 더 자세히 살펴보기 위해, 저자들은 먼저 ImageNet에서 사전 학습된 SiT 모델의 layer별 동작을 조사하였다. 특히, SiT와 DINOv2 모델 간의 표현 차이를 측정하는 데 초점을 맞추었다. 이를 semantic 차이, feature 정렬 진행 과정, 그리고 최종 feature 정렬이라는 세 가지 관점에서 분석하였다.

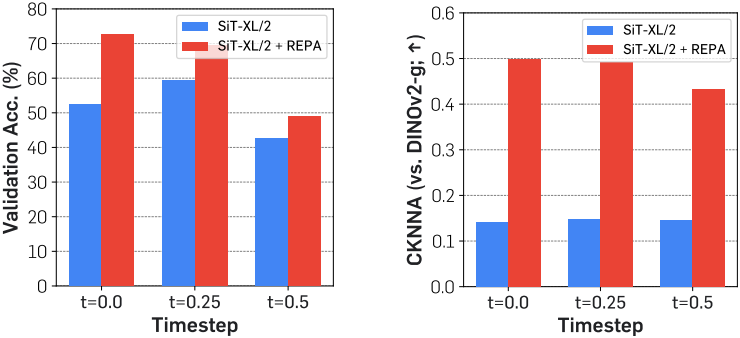
Semantic 차이의 경우, 700만 iteration의 학습을 거친 SiT 모델의 feature에 대한 linear probing 결과와 DINOv2 feature를 사용한 linear probing 결과를 비교하였다. SiT 모델은 글로벌하게 pooling된 hidden state에 대하여 linear probing을 수행한다. 다음으로, feature 정렬을 측정하기 위해 커널 정렬 metric인 CKNNA를 사용한다. CKNNA를 통해 서로 다른 표현 간의 정렬을 정량적으로 평가할 수 있다.

DiT는 SOTA 비전 인코더와 비교했을 때 상당한 semantic 격차를 보인다.

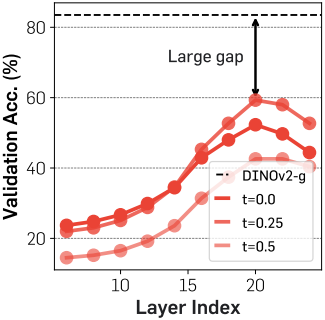
위 그림에서 볼 수 있듯이, 사전 학습된 SiT의 hidden state 표현은 20번째 layer에서 비교적 높은 linear probing 피크를 달성한다. 그러나 그 성능은 DINOv2에 비해 여전히 현저히 낮아 두 표현 간에 semantic 격차가 상당함을 나타낸다. 또한, 이 피크에 도달한 후 linear probing 성능이 급격히 저하되는 것을 발견했는데, 이는 SiT가 고주파 디테일을 포함하는 이미지를 생성하기 위해 풍부한 semantic 표현 학습에만 집중하는 방식에서 벗어나야 함을 시사한다.

Diffusion 표현은 이미 다른 시각적 표현과 약하게 정렬되어 있다.

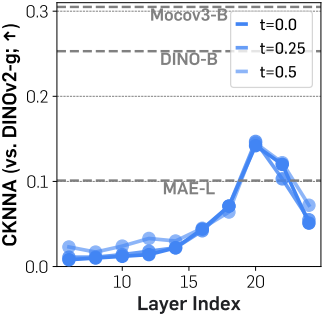
위 그림에서는 CKNNA를 사용하여 SiT와 DINOv2 간의 표현 정렬을 보여준다. SiT 모델 표현은 MAE보다 더 나은 정렬을 보이지만, 정렬 점수는 다른 self-supervised learning 방법과 DINOv2 간의 정렬 점수보다 여전히 낮다. 이러한 결과는 SiT 표현이 DINOv2 표현과 어느 정도 정렬되지만, 그 정렬은 여전히 ​​약하다는 것을 시사한다.

모델 크기가 커지고 오래 학습할수록 정렬도가 향상된다.

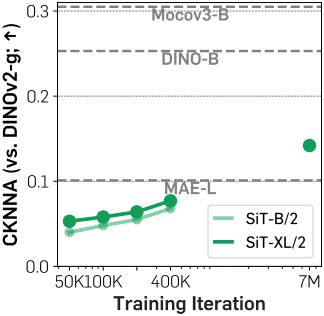
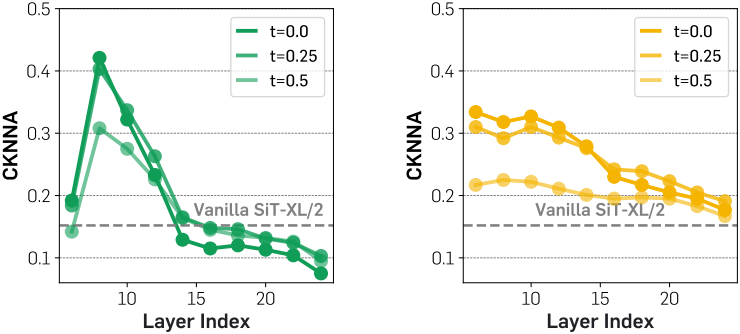
또한 저자들은 다양한 모델 크기와 학습 iteration 수에 따른 CKNNA 값을 측정했다. 위 그림에서 볼 수 있듯이, 모델 크기가 커지고 학습이 길어질수록 정렬도가 향상되는 것을 확인할 수 있다. 그러나 700만 iteration 후에도 정렬도는 여전히 낮으며, 다른 self-supervised learning 기반 비전 인코더 간의 정렬도 수준에는 미치지 못한다.

이러한 결과들은 SiT 모델에만 국한된 것이 아니라 다른 denoising 기반 transformer에서도 관찰된다.

3. Representation alignment with self-supervised representations

REPA는 모델의 hidden state에 대한 패치 단위 projection을 사전 학습된 self-supervised 시각적 표현과 정렬한다. 특히, 깨끗한 이미지 표현을 타겟으로 사용하였다. 이 정규화의 목표는 diffusion transformer의 hidden state가 유용한 semantic 정보를 포함하는 noise가 있는 입력으로부터 noise에 불변하는 깨끗한 시각적 표현을 예측하도록 하는 것이다. 이는 이후 layer가 타겟을 재구성하는 데 의미 있는 guidance를 제공한다.

$f$를 사전 학습된 인코더라고 하고 깨끗한 이미지 \(\textbf{x}_\ast\)를 고려하자. \(\textbf{y}_\ast = f(\textbf{x}_\ast) \in \mathbb{R}^{N \times D}\)를 인코더 출력이라고 하자. $N$과 $D$는 각각 $f$의 패치 개수와 임베딩 차원이다. MLP로 구성된 학습 가능한 projection head \(h_\phi\)를 사용하여 \(\textbf{h}_t = f_\theta (\textbf{z}_t)\)의 차원을 \(h_\phi (\textbf{h}_t) \in \mathbb{R}^{N \times D}\)로 맞춘다.

REPA는 사전 학습된 표현 \(\textbf{y}_\ast\)와 hidden state \(\textbf{h}_t\) 사이의 패치별 유사성을 최대화함으로써 정렬을 달성한다.

\[\begin{equation} \mathcal{L}_\textrm{REPA} (\theta, \phi) = - \mathbb{E}_{\textbf{x}_\ast, \epsilon, t} \left[ \frac{1}{N} \sum_{n=1}^N \textrm{sim} (\textbf{y}_\ast^{[n]}, h_\phi (\textbf{h}_t^{[n]})) \right] \end{equation}\]

($n$은 패치 인덱스, $\textrm{sim}(\cdot, \cdot)$은 미리 정의된 유사도 함수)

이 정규화 loss를 원래의 diffusion loss에 추가한다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{diffusion} + \lambda \mathcal{L}_\textrm{REPA} \end{equation}\]

본 논문에서는 주로 DiT에서 사용되는 Improved DDPM과 SiT에서 사용되는 linear stochastic interpolants라는 두 가지 인기 있는 loss에 대한 이러한 정규화의 영향을 조사하였지만, 다른 loss도 고려할 수 있다.

Experiments

1. Component-wise analysis

다음은 구성 요소별 분석 결과이다.

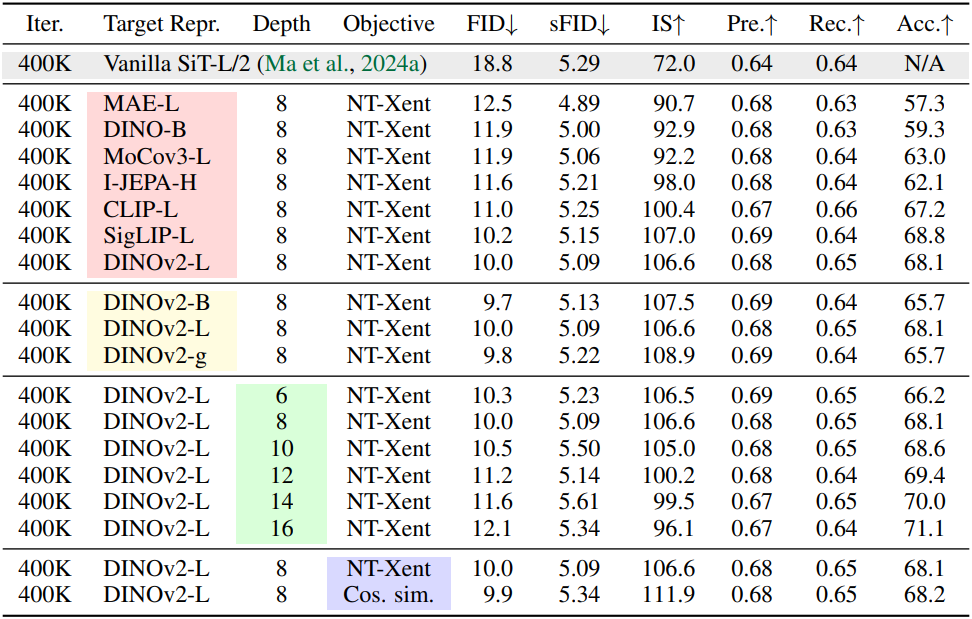
다음은 REPA의 scalability를 나타낸 결과이다.

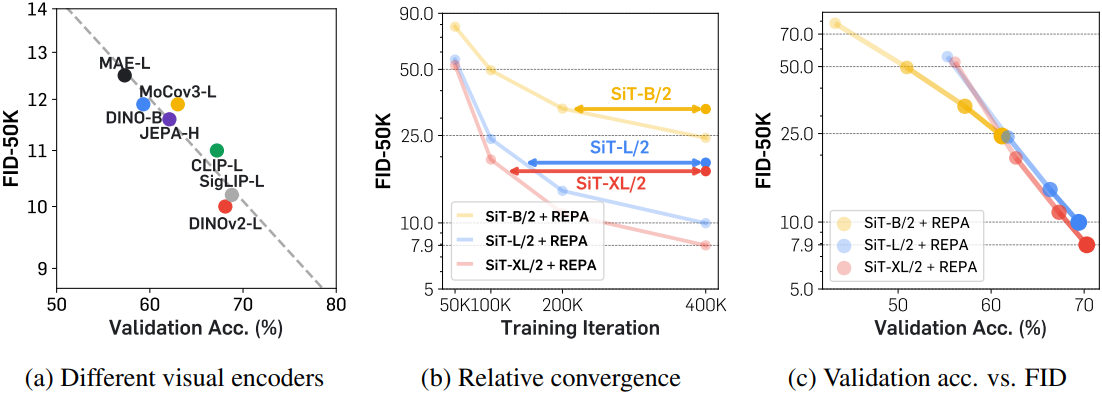
2. System-level comparison

다음은 기본 DiT 및 SiT와 FID를 비교한 결과이다.

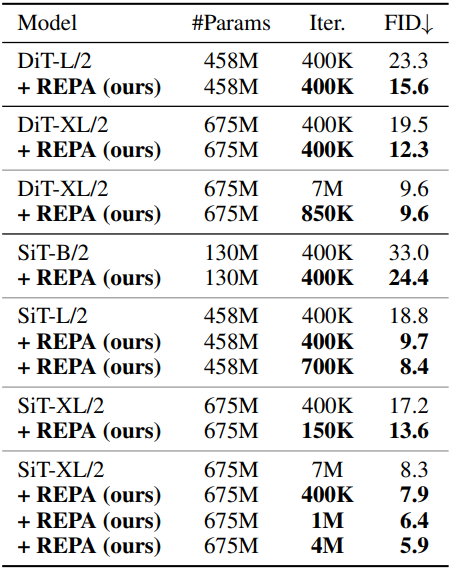
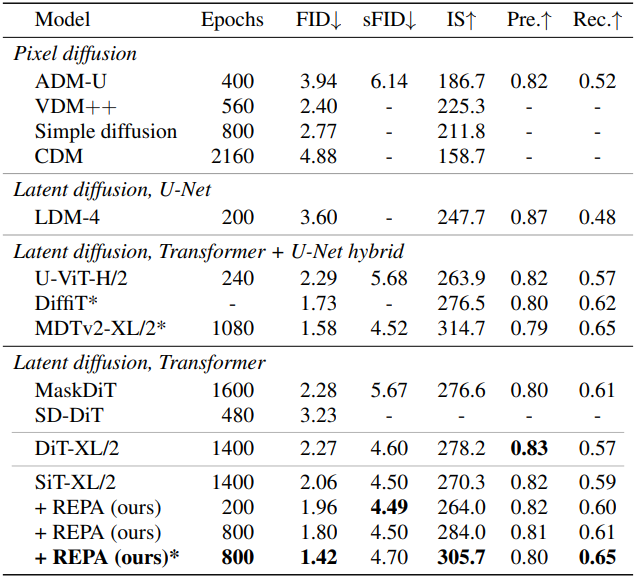
다음은 다른 SOTA 모델들과 비교한 결과이다. (*는 CFG 사용)

다음은 학습 iteration에 따른 생성된 샘플들을 비교한 것이다.

3. Ablation studies

다음은 timestep에 따른 표현 격차를 비교한 결과이다.

다음은 타겟 표현에 따른 표현 정렬을 비교한 결과이다.

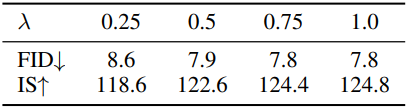
다음은 $\lambda$에 따른 FID와 IS를 비교한 결과이다.