[논문리뷰] Relightable 3D Gaussian: Real-time Point Cloud Relighting with BRDF Decomposition and Ray Tracing

arXiv 2023. [Paper] [Page] [Github]
Jian Gao, Chun Gu, Youtian Lin, Hao Zhu, Xun Cao, Li Zhang, Yao Yao
Nanjing University | Fudan University
27 Nov 2023

Introduction

사실적인 렌더링을 위해 멀티뷰 이미지에서 3D 장면을 재구성하는 것은 컴퓨터 비전과 그래픽이 교차하는 근본적인 문제이다. 최근 NeRF의 개발로 미분 가능한 렌더링 기술이 엄청난 인기를 얻었으며 이미지 기반의 novel view synthesis에서 탁월한 능력을 입증했다. 그러나 NeRF의 보급에도 불구하고 암시적 표현의 학습과 렌더링에는 상당한 시간 투자가 필요하므로 실시간 렌더링에 극복할 수 없는 과제가 있다. 느린 샘플링 문제를 해결하기 위해 그리드 기반 구조 활용 및 고급 baking을 위한 사전 계산(pre-computation)을 포함하여 다양한 가속 알고리즘이 제안되었다.

최근에는 3D Gaussian Splatting(3DGS)이 제안되어 큰 주목을 받았다. 이 방법은 3D 장면을 표현하기 위해 3D Gaussian point 집합을 사용하고 타일 기반 rasterization을 통해 지정된 뷰에 이러한 점들을 투영한다. 각 3D Gaussian point의 속성은 포인트 기반의 미분 가능한 렌더링을 통해 최적화된다. 특히 3DGS는 가장 효율적인 Instant-NGP와 동등한 학습 속도로 이전의 SOTA 방법과 비슷하거나 이를 능가하는 품질로 실시간 렌더링을 달성한다. 그러나 현재 3DGS는 다양한 조명 조건에서 relighting될 수 있는 장면을 재구성할 수 없으므로 이 방법은 novel view synthesis에만 적용할 수 있다. 또한 사실적인 렌더링을 달성하는 데 중요한 구성 요소인 ray tracing 추적은 포인트 기반 표현에서 해결되지 않은 과제로 남아 있어 3DGS를 그림자 및 빛 반사와 같은 렌더링 효과에서 제한한다.

본 논문에서는 재구성된 3D 포인트 클라우드의 relighting, 편집, ray tracing을 지원하는 3D Gaussian 표현만을 기반으로 하는 포괄적인 렌더링 파이프라인을 개발하는 것을 목표로 하였다. 추가적으로 각 3D Gaussian point에 normal(법선), BRDF 속성, 입사광 정보를 할당하여 포인트별 빛 반사율을 모델링하였다. 3DGS의 일반 볼륨 렌더링과 달리 PBR(물리 기반 렌더링)을 적용하여 각 3D Gaussian point에 대한 PBR color를 얻은 다음 알파 합성을 통해 해당 이미지 픽셀에 대해 렌더링된 색상을 얻는다. 견고한 재료 및 조명 추정을 위해 입사광을 글로벌 환경 맵과 로컬 입사광 필드로 분할했다. 포인트 기반 ray tracing 문제를 해결하기 위해 각 3D Gaussian point의 효율적인 visibility baking과 그림자 효과가 있는 장면의 사실적인 렌더링을 가능하게 하는 Bounding Volume Hierarchy (BVH) 기반의 새로운 tracing 방법을 제안하였다. 또한 최적화 중에 재질 및 조명 모호성을 완화하기 위해 새로운 base color 정규화, BRDF smoothness, 조명 정규화를 포함하는 적절한 정규화가 도입되었다.

Relightable 3D Gaussians

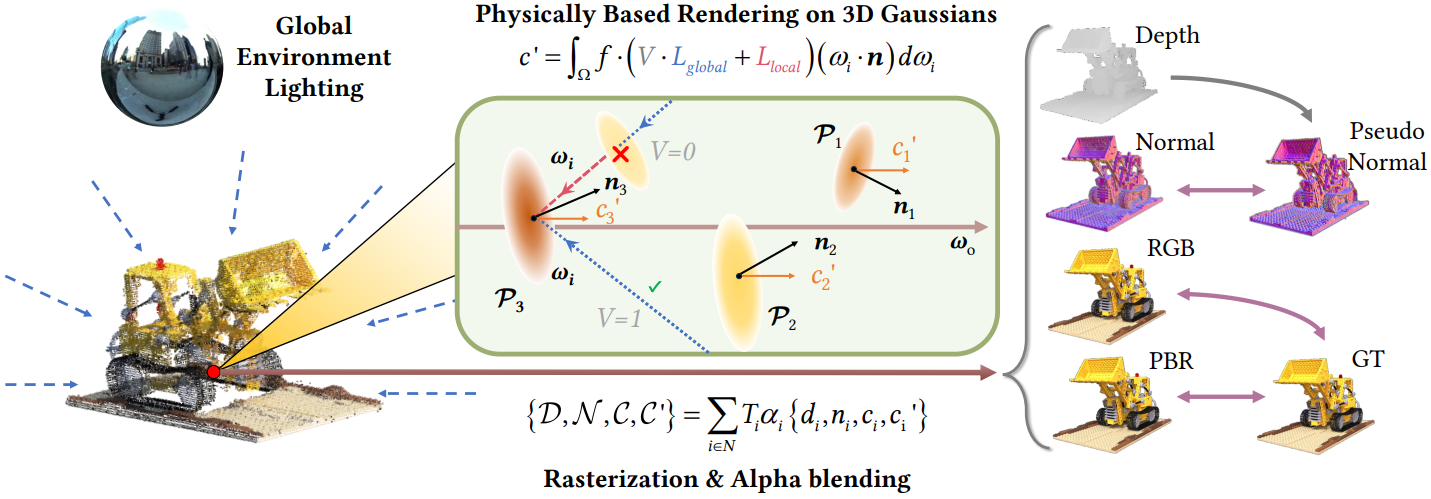
본 논문은 3DGS를 기반으로 한 멀티뷰 이미지 컬렉션에서 재료와 조명을 분해하기 위해 맞춤화된 새로운 파이프라인을 도입한다. 이 파이프라인의 개요는 위 그림에 나와 있다.

1. Geometry Enhancement

장면 형상, 특히 표면 법선은 사실적인 물리 기반 렌더링에 필수적이다. 따라서 강력한 BRDF 추정을 위해 장면 형상을 더욱 정규화한다.

Normal Estimation

저자들은 각 3D Gaussian에 대해 normal 속성 $n$을 통합하고 이를 PBR에 최적화하는 전략을 고안하였다.

한 가지 방법은 3D Gaussian의 공간적 평균을 기존 포인트 클라우드로 처리하고 로컬 평면성(local planarity) 가정을 기반으로 normal을 추정하는 것이다. 그러나 이 접근 방식은 포인트가 sparse하고 더 중요하게는 포인트의 부드러운 특성으로 인해 방해를 받는다. 이는 물체 표면과의 부정확한 정렬을 의미하며 이는 부정확한 추정으로 이어질 수 있다.

이러한 제한 사항을 해결하기 위해 저자들은 역전파를 통해 초기 랜덤 벡터로부터 $n$을 최적화하는 방법을 제안하였다. 이 프로세스에는 지정된 시점에 대한 depth map과 normal map의 렌더링이 수반된다.

\[\begin{equation} \{\mathcal{D}, \mathcal{N}\} = \sum_{i \in N} T_i \alpha_i \{d_i, n_i\} \end{equation}\]

여기서 $d_i$와 $n_i$는 포인트의 깊이와 normal을 나타낸다. 그런 다음 로컬 평면성(local planarity) 가정 하에 렌더링된 깊이 $\mathcal{D}$로부터 계산된 렌더링된 normal $\mathcal{N}$과 pseudo normal \(\tilde{\mathcal{N}}\) 사이의 일관성을 장려한다. Normal 일관성은 다음과 같이 정량화된다.

\[\begin{equation} \mathcal{L}_n = \| \mathcal{N} - \tilde{\mathcal{N}} \|_2 \end{equation}\]

Multi-View Stereo as Geometry Clues

실제 장면은 종종 복잡한 기하학적 구조를 나타내며, 이는 주로 일반적인 기하학적 모양의 모호성으로 인해 3DGS가 만족스러운 기하학적 구조를 생성하는 데 상당한 어려움을 겪는다. 이 문제를 해결하기 위해 저자들은 강력한 성능과 일반화 가능성을 보여주는 Multi-View Stereo(MVS)의 기하학적 단서를 통합할 것을 제안하였다. Vis-MVSNet을 활용하여 뷰별 depth map을 추정한 다음 photometric 일관성과 기하학적 일관성을 검사하여 필터링한다. 렌더링된 깊이 $\mathcal{D}$와 필터링된 MVS depth map \(\mathcal{D}_\textrm{mvs}\) 사이의 일관성을 다음과 같이 보장한다.

\[\begin{equation} \mathcal{L}_d = \| \mathcal{D} - \mathcal{D}_\textrm{mvs} \|_1 \end{equation}\]

\(\mathcal{L}_n\)과 비슷하게 렌더링된 normal $\mathcal{N}$과 MVS 깊이 \(\mathcal{D}_\textrm{mvs}\)로부터 계산된 normal \(\tilde{\mathcal{N}}_\textrm{mvs}\) 사이에도 normal 일관성 \(\mathcal{L}_{n, \textrm{mvs}}\)가 적용된다.

2. BRDF and Light Modeling

Recap on the Rendering Equation

렌더링 방정식은 재료 특성과 형상을 고려하여 표면과의 조명 상호 작용을 다음과 같이 모델링한다.

\[\begin{equation} L_o (\omega_o, x) = \int_\Omega f (\omega_o, \omega_i, x) L_i (\omega_i, x) (\omega_i \cdot n) d \omega_i \end{equation}\]

여기서 $x$와 $n$은 surface point와 normal 벡터이다. $f$는 BRDF 속성을 모델링하고, $L_i$와 $L_o$는 $\omega_i$와 $\omega_o$ 방향으로 들어오고 나가는 빛의 radiance(휘도)를 나타낸다. $\Omega$는 표면 위의 반구형 도메인을 의미한다.

이전 방법들은 일반적으로 미분 가능한 렌더링을 통해 광선과 표면 사이의 교차점을 획득하는 것으로 시작하는 순차적 파이프라인을 채택한 다음 PBR을 용이하게 하기 위해 이러한 점에 렌더링 방정식을 적용하였다. 그러나 이 접근 방식은 본 논문의 프레임워크의 맥락에서 심각한 문제가 발생한다. 렌더링된 depth map에서 표면을 추출하는 것이 가능하지만 이러한 surface point에서 좌표 기반의 글로벌 neural field를 쿼리하면 각 iteration에서 전체 이미지를 렌더링하기 위해 렌더링 방정식을 수백만 개의 surface point에 적용해야 하므로 과도한 계산 비용이 부과된다.

저자들은 이 문제를 해결하기 위해 먼저 Gaussian 레벨에서 PBR color \(\{c_i^\prime\}_{i=0}^N\)을 계산한 후 알파 블렌딩을 통해 PBR 이미지 $\mathcal{C}^\prime$을 렌더링하는 것을 제안하였다.

\[\begin{equation} \mathcal{C}^\prime = \sum_{i \in N} T_i \alpha_i c_i^\prime \end{equation}\]

이 방법은 두 가지 이유로 인해 더 효율적이다.

1. PBR은 모든 픽셀이 아닌 더 적은 수의 3D Gaussian에서 수행된다. 각 Gaussian은 스케일을 기반으로 여러 픽셀에 영향을 미치기 때문이다.
2. 각 Gaussian에 대해 개별 속성을 할당함으로써 글로벌한 neural field가 필요하지 않다.

BRDF Parameterization

위에서 설명한 대로 각 Gaussian에 추가 BRDF 속성 (base color $b \in [0, 1]^3$, roughness $r \in [0, 1]$, metallic $m \in [0, 1]$)을 할당한다. 저자들은 NeILF에서와 같이 단순화된 Disney BRDF 모델을 채택하였다. BRDF 함수 $f$는 diffuse 항 $f_d = \frac{1-m}{\pi} \cdot b$와 specular 항으로 나뉜다.

\[\begin{equation} f_s (\omega_o, \omega_i) = \frac{D(h; r) \cdot F(\omega_o, h; b, m) \cdot G(\omega_i, \omega_o, h; r)}{(n \cdot \omega_i) \cdot (n \cdot \omega_o)} \end{equation}\]

여기서 $h$는 half vector (camera vector와 light vector의 중간 벡터)이고, $D$, $F$, $G$는 각각 정규 분포 함수, Fresnel 항 및 geometry 항을 나타낸다.

Incident Light Modeling

각 Gaussian에 대해 NeILF를 직접 최적화하는 것은 지나치게 제한되지 않을 수 있으므로 입사광을 외형에서 정확하게 분해하기가 어렵다. 입사광을 글로벌 성분과 로컬 성분으로 나누어 prior를 적용한다. $\omega_i$ 방향에서 Gaussian으로 샘플링된 입사광은 다음과 같다.

\[\begin{equation} L_i (\omega_i) = V(\omega_i) \cdot L_\textrm{global} (\omega_i) + L_\textrm{local} (\omega_i) \end{equation}\]

여기서 visibility 항 $V(\omega_i)$와 local light 항 \(L_\textrm{local}(\omega_i)\)는 각 Gaussian에 대한 Spherical Harmonics(SH)로 parameterize되며 각각 $v$와 $l$로 표시된다. Global light 항 $l^\textrm{env}$은 글로벌하게 공유되는 SH로 parameterize된다. 각 3D Gaussian에 대해 피보나치 샘플링을 통해 반구 공간에 대한 $N_s$개의 입사 방향을 샘플링하여 수치적 적분을 한다. 그러면 Gaussian의 PBR color는 다음과 같다.

\[\begin{equation} c^\prime (\omega_o) = \sum_{i=0}^{N_s} (f_d + f_s (\omega_o, \omega_i)) L_i (\omega_i) (\omega_i \cdot n) \Delta \omega_i \end{equation}\]

요약하자면, 본 논문의 방법은 3D 장면을 relightable 3D Gaussian 집합과 글로벌한 환경 조명 $l^\textrm{env}$로 나타낸다. 여기서 $i$번째 가우시안 \(\mathcal{P}_i\)는 다음과 같이 parameterize된다.

\[\begin{equation} \{\mu_i, q_i, s_i, o_i, c_i, n_i, b_i, r_i, m_i, v_i, l_i\} \end{equation}\]

3. Regularization

NeILF에서 지적했듯이 최적화 과정에서 재료와 조명 사이에는 모호성이 존재한다. 이 문제를 해결하기 위해 재질과 조명의 그럴듯한 분해를 촉진하기 위해 정규화가 구현되었다.

Base Color Regularization

이상적인 base color는 그림자와 하이라이트가 없는 상태에서 관찰된 이미지 $\mathcal{C}$와 특정 색조 유사성을 나타내야 한다는 전제에 따라 base color에 대한 새로운 정규화를 도입한다. 렌더링된 base color \(\mathcal{C}_b = \sum_{i \in N} T_i \alpha_i b_i\)에 대한 레퍼런스 역할을 하는 그림자와 하이라이트가 감소된 이미지 \(\mathcal{C}_\textrm{target}\)을 생성한다.

\[\begin{aligned} \mathcal{L}_b &= \| \mathcal{C}_b - \mathcal{C}_\textrm{target} \|_1 \\ \mathcal{C}_\textrm{target} &= w \cdot \mathcal{C}_h + (1 - w) \cdot \mathcal{C}_s \\ \mathcal{C}_s &= 1 - (1 - \mathcal{C}) \cdot (1 - \mathcal{C}) \\ \mathcal{C}_h &= \mathcal{C} \cdot \mathcal{C} \\ w &= 1/(1 + \exp(−\psi(\mathcal{C}_v − 0.5))) \end{aligned}\]

여기서 \(\mathcal{C}_s\)와 \(\mathcal{C}_h\)는 각각 그림자가 없는 이미지와 하이라이트가 없는 이미지이다. $w$는 가중치이며 $\psi$는 실험적으로 5로 설정되고 \(\mathcal{C}_v = \max (R, G, B)\)는 HSV 색상의 value(명도) 성분이다. max 연산이 demodulation에 거의 근접하므로 value 성분은 광원의 색상과 관계없이 하이라이트와 그림자를 효과적으로 구분한다.

Light Regularization

백색 입사광을 가정하여 조명 정규화를 적용한다.

\[\begin{equation} \mathcal{L}_\textrm{light} = \sum_c (L_c - \frac{1}{3} \sum_c L_c), \quad c \in \{R, G, B\} \end{equation}\]

Bilateral Smoothness

부드러운 색상이 있는 영역에서는 BRDF 속성이 크게 변하지 않을 것으로 예상된다. Metallic에 대한 smoothness 제약 조건을 다음과 같이 정의한다.

\[\begin{equation} \mathcal{L}_\textrm{s, m} = \| \nabla M \| \exp (- \| \nabla C_\textrm{gt} \|) \end{equation}\]

여기서 $M$은 \(M = \sum_{i \in N} T_i \alpha_i m_i\)로 주어진 렌더링된 metallic map이다. 마찬가지로 roughness와 base color에 대한 smoothness 제약 조건 \(\mathcal{L}_\textrm{s,r}\)과 \(\mathcal{L}_\textrm{s,b}\)도 정의한다.

Point-based Ray Tracing

본 논문은 조명이 밝은 3D Gaussian에 정확한 그림자 효과를 적용한 실시간 및 사실적인 렌더링을 위해 새로운 포인트 기반 ray tracing 방식을 도입하였다.

1. Ray Tracing on 3D Gaussians

3D Gaussian에 대해 본 논문이 제안한 ray tracing 기술은 Bounding Volume Hierarchy (BVH)를 기반으로 구축되어 광선을 따라 visibility를 효율적으로 쿼리할 수 있다. 본 논문의 방법은 병렬성을 최대화하고 실시간 BVH 구성을 용이하게 하는 binary radix tree를 구성하는 in-place 알고리즘인 Maximizing Parallelism in the Construction of BVHs, Octrees, and k-d Trees 논문의 아이디어를 채택하였다. 이 알고리즘은 학습 프로세스 내에서 ray tracing을 통합하는 데 중추적인 역할을 한다. 구체적으로, 각 iteration에서 3D Gaussian으로부터 binary radix tree를 구성한다. 여기서 각 leaf node는 Gaussian에 대한 bounding box를 나타내고 각 internal node는 두 자식의 bounding box를 나타낸다.

가장 가까운 교차점만 필요한 불투명 다각형 메쉬를 사용한 ray tracing과 달리, 반투명 Gaussian을 사용한 ray tracing에서는 잠재적으로 광선의 투과율에 영향을 미칠 수 있는 모든 Gaussian을 고려해야 한다. 3DGS에서는 픽셀에 대한 Gaussian의 기여도가 2D 픽셀 공간에서 계산된다. 3D Gaussian을 2D Gaussian으로 변환하는 데는 근사가 포함되어 픽셀 공간에서 2D Gaussian과 동일한 영향을 미치는 동등한 3D 포인트의 식별이 복잡해진다. 따라서 3D Gaussian의 기여도가 최고조에 달하는 광선을 따라 영향력 있는 3D 포인트의 위치를 대략적으로 추정한다.

\[\begin{equation} t_j = \frac{(\mu - r_o)^\top \Sigma r_d}{r_d^\top \Sigma r_d} \end{equation}\]

여기서 $r_o$와 $r_d$는 광선의 원점과 방향 벡터를 나타내며, 앞서 언급한 $\omega_i$에 해당한다. 이어서, 광선에 대한 Gaussian의 기여도 $\alpha_j$를 다음과 같이 결정할 수 있다.

\[\begin{equation} \alpha_j = o_i G(r_o + t_j r_d). \end{equation}\]

광선에 따른 투과율 방정식 $T_i = \prod_{j=1}^{i−1} (1 − \alpha_j)$을 고려하면 $\alpha_j$의 순서가 $T_i$에 영향을 미치지 않는다는 것이 분명하다. 이는 광선을 따라 가우시안이 만나는 순서가 전반적인 투과율에 영향을 미치지 않음을 나타낸다.

위 그림에서 볼 수 있듯이 binary radix tree의 root node부터 시작하여 광선과 각 node의 자식들의 경계 볼륨 간에 교차 테스트가 반복적으로 수행된다. Leaf node에 도달하면 관련 Gaussian이 식별된다. 이 순회를 통해 투과율 $T$는 점진적으로 감쇠된다.

\[\begin{equation} T_i = (1 - \alpha_{i-1}) T_{i-1}, \quad \textrm{for} \; i = 1, \ldots, j-1 \quad \textrm{with} \; T_1 = 1 \end{equation}\]

Ray tracing 속도를 높이기 위해 광선의 투과율이 특정 임계값 $T_\textrm{min}$ 아래로 떨어지면 프로세스가 종료된다.

2. Visibility Estimation and Baking

저자들은 local light과 global light의 분해에서 잠재적인 모호성을 확인했다. 합리적인 분해를 위한 중요한 visibility 항 $V$는 제안된 ray tracing을 통해 계산될 수 있다. 그러나 계산 복잡성으로 인해 최적화 중에 ray tracing을 통해 visibility를 직접 쿼리하는 것은 바람직하지 않다. 대신, 단일 광선의 visibility는 3D Gaussian의 형상에만 의존한다는 관찰을 기반으로 먼저 해당 경로를 따라 해당 Gaussian의 $\alpha_i$를 통합하여 광선의 visibility를 3D Gaussian에 baking한 다음 학습 가능한 visibility를 추적된 visibility $T$로 supervise한다.

\[\begin{equation} \mathcal{L}_v = \| V - T \|_2 \end{equation}\]

Visibility baking으로 인해 ray tracing을 수행하는 데 필요한 랜덤 광선 수가 크게 줄어들기 때문에 supervision에는 큰 부담이 되지 않는다. 게다가 baking된 visibility는 정확한 shading 효과로 실시간 렌더링을 크게 촉진한다.

3. Realistic Relighting

저자들은 relightable 3D Gaussian을 위해 맞춤화된 그래픽 파이프라인을 구성하였다. 이 파이프라인은 다양한 장면에 대한 적응성을 보여주며 다양한 환경 맵에서 원활한 relighting을 가능하게 한다. 각각 relightable 3D Gaussian 집합으로 표시되는 여러 물체를 고유한 환경 맵 아래의 새로운 장면으로 결합할 때 파이프라인은 먼저 ray tracing을 통해 각 Gaussian point에 대해 baking한 visibility 항 $v$를 fine-tuning하여 물체 사이의 가려짐 관계를 정확하게 업데이트한다. 그 후 렌더링 프로세스는 Gaussian 레벨에서 PBR을 적용하는 것으로 시작하여 알파 블렌딩을 활용하는 것으로 마무리된다. 앞서 언급한 접근 방식을 통해 정확한 그림자 효과로 이미지를 효율적으로 렌더링할 수 있다. 또한 오프라인 렌더링의 경우 3D Gaussian에 대한 ray tracing에만 의존하여 훨씬 뛰어난 이미지 품질을 달성할 수 있다.

Experiments

1. Training Details

안정적인 최적화를 보장하기 위해 학습 절차는 두 단계로 나뉜다. 먼저, 추가 normal $n$으로 보강된 3DGS 모델을 최적화한다. 또한 적응형 밀도 제어를 위해 normal gradient 조건을 추가한다. 그 후, 첫 번째 단계에서 이미 안정된 형상을 사용하여 visibility 항 $v$를 baking하는 ray tracing 방법으로 시작한 다음 포괄적인 파이프라인을 사용하여 전체 파라미터들을 최적화한다. 두 번째 단계에서는 PBR에 대해 Gaussian당 $N_s = 24$개의 광선을 샘플링한다. 아래 표는 사용된 loss와 그 가중치의 전체 목록이다. 초기 단계에서는 30,000번의 iteration, 두 번째 단계에서는 10,000번의 iteration으로 모델을 학습시킨다. 모든 실험은 NVIDIA GeForce RTX 3090 GPU 1개에서 수행되었다.

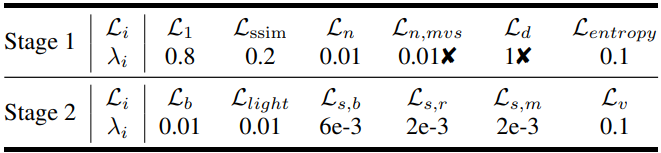
($\unicode{x2718}$: 합성 데이터셋에서는 사용되지 않았음)

2. Performance

다음은 NeRF 합성 데이터셋에서의 novel view synthesis 결과를 정량적으로 비교한 표이다.

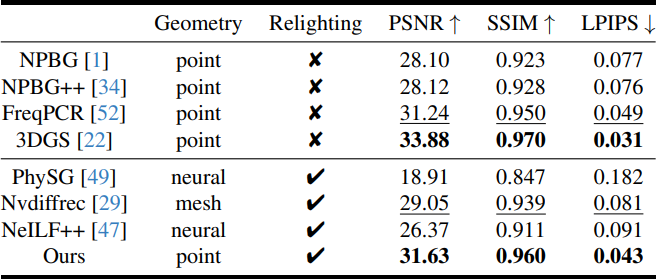
다음은 NeRF 합성 데이터셋과 DTU 데이터셋에서 정성적으로 비교한 결과이다.

다음은 DTU 데이터셋에서의 결과를 다른 방법들과 비교한 표이다.

다음은 BRDF 추정 결과를 시각화한 것이다.

3. Ablation Study

다음은 주요 구성 요소에 대한 ablation 결과이다.

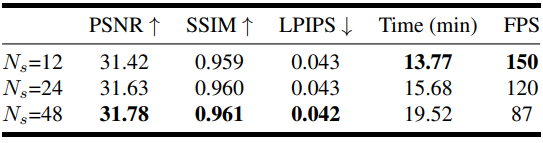
다음은 샘플 수에 대한 ablation 결과이다.