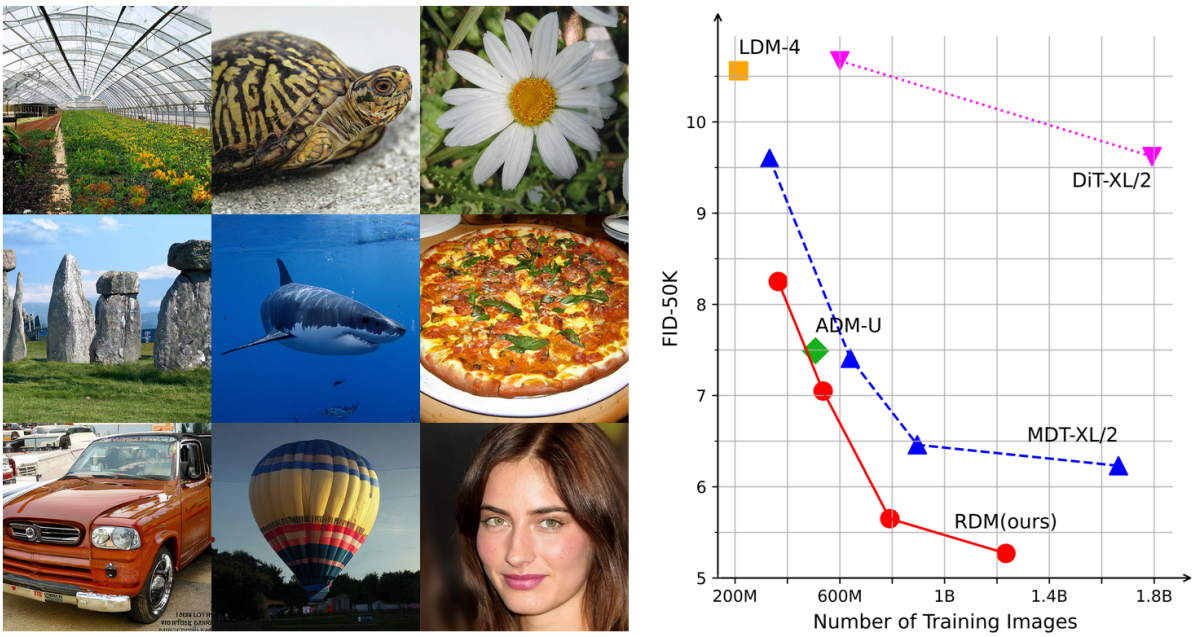
[논문리뷰] Relay Diffusion: Unifying diffusion process across resolutions for image synthesis (RDM)

ICLR 2024 (Spotlight). [Paper] [Github]
Jiayan Teng, Wendi Zheng, Ming Ding, Wenyi Hong, Jianqiao Wangni, Zhuoyi Yang, Jie Tang
Tsinghua University | Zhipu AI
4 Sep 2023

Introduction

Diffusion model은 GAN과 autoregressive model의 뒤를 이어 최근 몇 년 동안 가장 널리 사용되는 생성 모델이 되었다. 그러나 고해상도 이미지에 대한 diffusion model을 학습하는 데는 여전히 과제가 존재한다. 보다 구체적으로 말하면 두 가지 주요 장애물이 있다.

학습 효율성

다양한 해상도에 걸쳐 메모리와 계산 비용의 균형을 맞추기 위해 UNet이 장착되어 있지만 diffusion model에는 고해상도 이미지를 학습시키는 데 여전히 많은 양의 리소스가 필요하다. 널리 사용되는 솔루션 중 하나는 latent space에서 diffusion model을 학습시키고 결과를 다시 픽셀로 매핑하는 것이다. 이는 빠르지만 필연적으로 일부 낮은 수준의 아티팩트가 발생한다. 계단식 방법은 다양한 크기의 일련의 super-resolution diffusion model을 학습시키는데, 이는 효과적이지만 각 단계에 대해 개별적으로 완전한 샘플링이 필요하다.

Noise Schedule

Diffusion model에는 각 단계에서 Gaussian noise의 양을 제어하기 위한 noise schedule이 필요하다. Noise schedule의 설정은 성능에 큰 영향을 미치며, 대부분의 최신 모델은 linear schedule 또는 cosine schedule을 따른다. 그러나 이상적인 noise schedule은 해상도에 따라 달라진다. 결과적으로 32$\times$32 또는 64$\times$64 픽셀의 해상도를 위해 설계된 공통 schedule을 사용하여 고해상도 모델을 직접 학습시키는 데 최선의 성능을 발휘하지 못한다.

이러한 장애물은 이전 연구자들이 고해상도 이미지 생성을 위한 효과적인 end-to-end diffusion model을 확립하는 데 방해가 되었다. Diffusion Models Beat GANs on Image Synthesis 논문은 256$\times$256 ADM을 직접 학습하려고 시도했지만 계단식 파이프라인보다 성능이 훨씬 떨어지는 것을 발견했다. 다른 연구들 (ex. simple diffusion)도 고해상도 예시에 대한 noise schedule과 아키텍처의 hyperparameter를 신중하게 조정했지만 품질은 여전히 SOTA 계단식 방법과 비교할 수 없다.

본 논문의 의견으로는 계단식 방법은 학습 효율성과 noise schedule 모두에 기여한다.

1. 가장 효율적인 조합을 찾기 위해 각 단계마다 모델 크기와 아키텍처를 조정할 수 있는 유연성을 제공한다.
2. 저해상도 조건이 존재하면 초기 샘플링 step이 쉬워지므로 공통 noise schedule이 super-resolution 모델에 실행 가능한 baseline으로 적용될 수 있다.
3. 고해상도 이미지는 저해상도 이미지보다 인터넷에서 얻기가 더 어렵다.

계단식 방법은 저해상도 샘플의 지식을 활용하는 동시에 고해상도 이미지를 생성하는 능력을 유지할 수 있다. 따라서 현 단계에서 계단식 방식을 end-to-end 방식으로 완전히 대체하는 것은 유망한 방향이 아닐 수 있다.

계단식 방법의 단점도 분명하다.

1. 저해상도 부분이 결정되었음에도 불구하고 순수 noise에서 시작하는 완전한 diffusion model은 여전히 super-resolution을 위해 학습되고 샘플링되므로 시간이 많이 걸린다.
2. Ground-truth와 생성된 저해상도 조건 사이의 분포 불일치는 성능을 저하시키므로, 차이를 완화하기 위해 conditioning augmentation과 같은 트릭이 매우 중요해진다.
3. 고해상도 단계의 noise schedule은 아직까지 잘 연구되지 않았다.

본 논문에서는 이전 계단식 방법의 단점을 개선하기 위한 새로운 계단식 프레임워크인 Relay Diffusion Model (RDM)을 제시하였다. 각 단계에서 모델은 조건을 설정하고 순수한 noise에서 시작하는 대신 마지막 단계의 결과로부터 diffusion을 시작한다. 본 논문의 방법은 계단식 모델이 “릴레이 경주”처럼 함께 작동하기 때문에 relay diffusion model로 명명되었다.

Method

1. Motivation

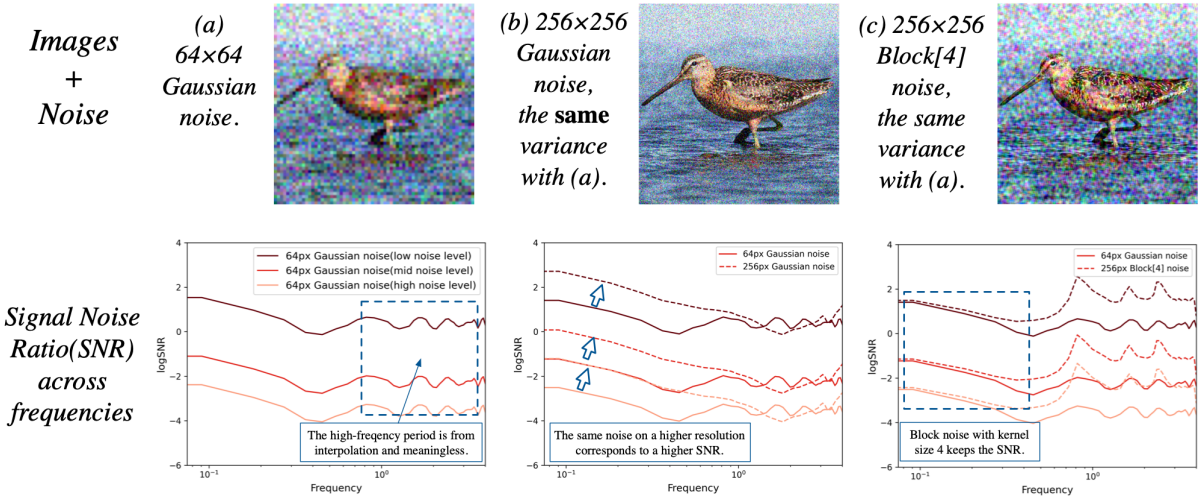
Noise schedule은 diffusion model에 매우 중요하며 해상도에 따라 다르다. 위 그림의 (a)와 (b)의 첫 번째 행을 보면, 64$\times$64 이미지를 적절하게 손상시키는 특정 noise level은 256$\times$256 이미지를 손상시키지 못할 수 있다. 저자들은 주파수 스펙트럼 관점의 분석이 이 현상을 잘 이해하는 데 도움이 될 수 있음을 발견했다.

Diffusion process의 푸리에 스펙트럼 분석

다양한 해상도의 자연 이미지를 다양한 주파수로 샘플링된 시각적 신호의 결과로 볼 수 있다. 64$\times$64 이미지와 256$\times256 이미지의 주파수 특성을 비교하기 위해 64$\times$64 이미지를 256$\times$256으로 업샘플링하고 Discrete Cosine Transformation (DCT)를 수행한 후 256-point DCT 스펙트럼에서 비교할 수 있다. 위 그림의 (a)의 두 번째 행은 다양한 주파수와 diffusion step에서의 신호 대 잡음비 (SNR)를 보여준다. 위 그림의 (b)를 보면 더 높은 해상도에서 동일한 noise level이 주파수 영역 (저주파 부분)에서 더 높은 SNR을 가져온다는 것을 분명히 알 수 있다.

특정 diffusion step에서 SNR이 높다는 것은 학습 중에 신경망이 입력 이미지를 더 정확하게 가정하지만 SNR이 증가한 후에는 초기 단계에서 그렇게 정확한 이미지를 생성하지 못할 수도 있음을 의미한다. 이러한 학습-inference 불일치는 샘플링 중에 step별로 누적되어 성능 저하로 이어진다.

고해상도 equivalence로서의 block noise

64$$\times64에서 256$\times$256으로 업샘플링한 후 64$\times$64의 독립적인 Gaussian noise는 4$\times$4 그리드의 noise가 되어 주파수 표현이 크게 변경된다. 결정론적 경계가 없는 $s \times s$-그리드 noise의 변형을 찾기 위해 본 논문은 Gaussian noise가 근처 위치와 상관되는 block noise를 제안하였다. 보다 구체적으로, noise $\epsilon_{x_0, y_0}$과 $\epsilon_{x_1, y_1}$ 사이의 공분산은 다음과 같이 정의된다.

\[\begin{equation} \textrm{Cov} (\epsilon_{x_0, y_0}, \epsilon_{x_1, y_1}) = \frac{\sigma^2}{s^2} \max (0, s - \textrm{dis} (x_0, x_1)) \max (0, s - \textrm{dis} (y_0, y_1)) \end{equation}\]

여기서 $\sigma^2$은 noise의 분산이고 $s$는 hyperparameter 커널 크기이다. 여기서 $\textrm{dis}(\cdot, \cdot)$ 함수는 Manhattan distance이다. 단순화를 위해 이미지의 위쪽 및 아래쪽 가장자리와 왼쪽 및 오른쪽 가장자리를 연결하여 결과를 얻는다.

\[\begin{equation} \textrm{dis} (x_0, x_1) = \min (\vert x_0 - x_1 \vert, x_\textrm{max} - \vert x_0 - x_1 \vert) \end{equation}\]

커널 크기 $s$의 block noise는 $s \times s$개의 독립적인 Gaussian noise를 평균하여 생성할 수 있다. 독립적인 Gaussian noise 행렬 $\epsilon$이 있다고 가정하면 block noise 구성 함수 $\textrm{Block}[s] (\cdot)$은 다음과 같이 정의된다.

\[\begin{equation} \textrm{Block}[s] (\epsilon)_{x,y} = \frac{1}{s} \sum_{i=0}^{s-1} \sum_{j=0}^{s-1} \epsilon_{x-i, y-j} \end{equation}\]

여기서 \(\textrm{Block}[s] (\epsilon)_{x,y}\)는 위치 $(x, y)$의 block noise이고 $\epsilon_{−x} = \epsilon_{x_\textrm{max} − x}$이다. 위 그림의 (c)는 256$\times$256에서 커널 크기 $s = 4$인 block noise가 64$\times$64 이미지의 독립적인 Gaussian noise와 유사한 주파수 스펙트럼을 가짐을 보여준다.

위의 분석은 초기 diffusion step에서 block noise를 도입하여 고해상도 이미지에 대한 end-to-end 모델을 설계할 수 있는 반면 계단식 모델은 이미 큰 성공을 거두었음을 나타내는 것으로 보인다. 따라서 계단식 모델의 재검토가 필요하다.

계단식 모델이 이 문제를 완화하는 이유는 무엇인가?

이전 연구들의 실험에서는 공정한 설정에서 계단식 모델이 end-to-end 모델보다 더 나은 성능을 발휘한다는 것을 이미 보여주었다. 이러한 모델들은 일반적으로 모든 step에서 동일한 noise schedule을 사용하는데, 계단식 모델이 SNR 증가에 영향을 받지 않는 이유는 무엇일까? 그 이유는 super-resolution step에서는 저해상도 조건이 초기 단계의 어려움을 크게 완화하므로 SNR이 높을수록 더 정확한 입력이 필요하고 정확도는 모델의 성능 범위 내에 있기 때문이다.

자연스러운 아이디어는 고해상도 단계의 저주파 정보가 이미 저해상도 조건에 의해 결정되었기 때문에 업샘플링된 결과에서 직접 생성을 계속하여 학습 및 샘플링 step을 모두 줄일 수 있다는 것이다. 그러나 저해상도 이미지의 생성은 완벽하지 않으므로, ground-truth와 생성된 저해상도 이미지 간의 분포 불일치를 해결하는 것이 우선이다.

2. Relay Diffusion

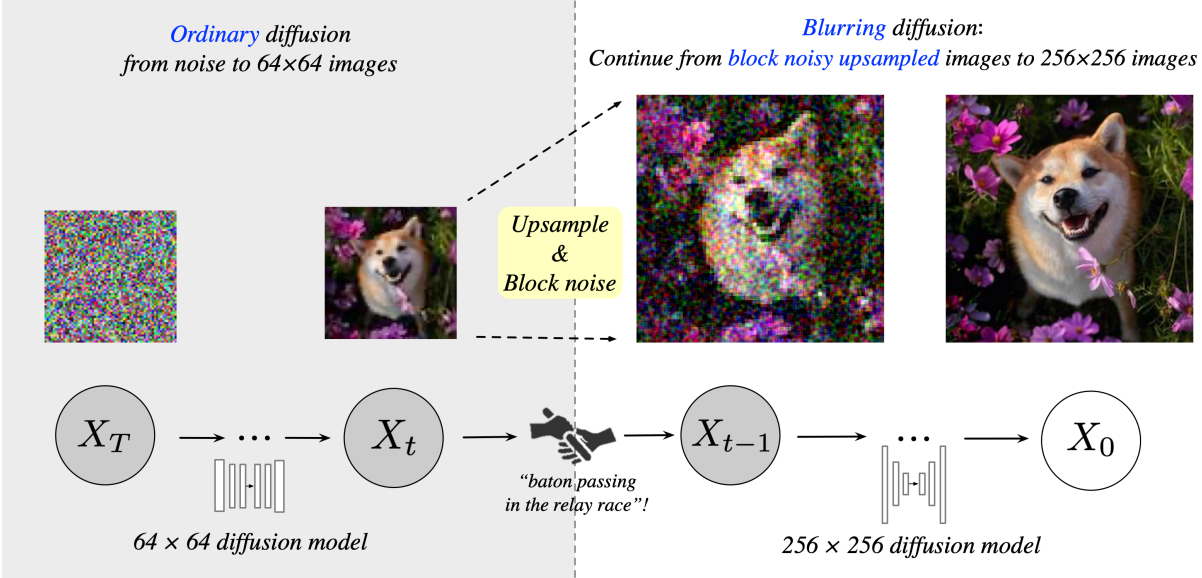
본 논문은 block noise와 patch-level blurring diffusion으로 단계를 연결하는 계단식 파이프라인인 relay diffusion model (RDM)을 제안하였다. CDM과 달리 RDM은 고해상도로 업샘플링할 때 저해상도로 생성된 이미지의 동등성을 고려한다. 생성된 64$\times$64 저해상도 이미지 $x_0^L = x^L + \epsilon_L$을 실제 분포의 샘플 $x^L$과 나머지 noise $\epsilon_L \sim \mathcal{N} (0, \beta_0^2 I)$로 분해할 수 있다고 가정한다. 앞서 언급했듯이 $\epsilon_L$의 256$\times$256 equivalence $\epsilon_H$는 분산 $\beta_0^2$을 갖는 block noise이다. 업샘플링 후에 $x^L$은 $x^H$가 되며, 여기서 각 4$\times$4 그리드는 동일한 픽셀 값을 공유한다. 이것을 patch-wise blurring diffusion의 시작 상태로 정의할 수 있다.

이미지의 전체 공간에 대해 열 방출 (heat dissipation)을 수행하는 blurring diffusion model과 달리, 본 논문은 업샘플링 스케일과 동일한 크기의 각 4$\times$4 패치에 대해 독립적으로 열 방출을 구현하는 것을 제안하였다. 먼저 일련의 patch-wise blurring matrix \(\{D_t^p\}\)를 정의한다. Forward process는 다음과 같이 표현된다.

\[\begin{equation} q(x_t \vert x_0) = \mathcal{N} (x_t \vert V D_t^p V^\top x_0, \sigma_t^2 I), \quad t \in \{0, \ldots, T\} \end{equation}\]

여기서 $V^\top$는 DCT의 projection matrix이고 $\sigma_t$는 noise의 분산이다. 여기서 $D_T^p$는 $x^H$와 동일한 분포에서 $V D_T^p V^\top x_0$을 보장하기 위해 선택되었다. 즉, blurring process가 궁극적으로 각 4$\times$4 패치의 픽셀 값을 동일하게 만든다는 의미이다.

RDM의 고해상도 단계의 목적 함수는 일반적으로 구현 시 EDM 프레임워크를 따른다. Loss function은 실제 데이터 $x$에 적합하도록 denoiser function $D$를 예측하여 정의되며 다음과 같다.

\[\begin{equation} \mathbb{E}_{x \sim p_\textrm{data}, t \sim \mathcal{U}(0,1), \epsilon \sim \mathcal{N}(0,I)} \| D (x_t, \sigma_t) - x \|^2 \\ \textrm{where} \quad x_t = \underbrace{V D_t^p V^\top}_{\textrm{blurring}} x + \frac{\sigma}{\sqrt{1 + \alpha^2}} (\epsilon + \alpha \cdot \underbrace{\textrm{Block}[s] (\epsilon')}_{\textrm{block noise}}) \end{equation}\]

여기서 $\epsilon$과 $\epsilon’$은 두 개의 독립적인 Gaussian noise이다. RDM과 EDM 학습의 주요 차이점은 손상된 샘플 $x_t$가 단순히 $x_t = x + \epsilon$이 아니라 블러링된 이미지, block noise, Gaussian noise가 혼합되어 있다는 것이다. 이상적으로는 noise가 block noise에서 고해상도 Gaussian noise로 점진적으로 전환되어야 하지만, block noise의 저주파 성분이 Gaussian noise보다 훨씬 크기 때문에 가중 평균 전략이 충분히 잘 수행된다. 고주파 성분의 경우에는 그 반대이다. $\alpha$는 hyperparameter이고 normalizer $\frac{1}{\sqrt{1 + \alpha^2}}$은 noise의 분산을 유지하는 데 사용된다. $\sigma^2$은 변경되지 않는다.

CDM과 비교하여 RDM의 장점은 다음과 같다.

1. RDM은 고해상도 단계에서 저주파 정보 재생성을 건너뛰고 학습 및 샘플링 step 수를 줄이기 때문에 더 효율적이다.
2. RDM은 저해상도 컨디셔닝과 conditioning augmentation 트릭을 제거하므로 더욱 간단하다. 저해상도 조건과의 cross-attention으로 인한 소비도 절약된다.
3. RDM은 Markovian denoising process이기 때문에 RDM은 성능 면에서 더 잠재력이 있다. 저해상도 이미지의 모든 아티팩트는 고해상도 단계에서 수정될 수 있으며, CDM은 저해상도 조건에 대응하도록 학습된다.

End-to-end 모델과 비교하였을 때 RDM은 모델 크기를 조정하고 더 많은 저해상도 데이터를 활용하는 데 더 유연하다.

3. Stochastic Sampler

RDM은 forward process에서 기존 diffusion model과 다르기 때문에 샘플링 알고리즘도 변경해야 한다. 본 논문은 1차 sampler와 2차 sampler (Heun’s method) 사이를 전환할 수 있는 유연성으로 인해 EDM sampler에 중점을 두었다.

Heun’s method은 1차 샘플링의 correction을 위한 추가 단계를 도입한다. 1차 샘플링 step의 업데이트 방향은 기울기 항

\[\begin{equation} d_n = \frac{x_n - x_\theta (x_n, \sigma_{t_n})}{\sigma_{t_n}} \end{equation}\]

에 의해 제어된다. Correction step에서는 평균 기울기 항 $\frac{d_n + d_{n−1}}{2}$로 현재 상태를 업데이트한다. Heun’s method는 $t_n$과 $t_{n−1}$ 사이의 기울기 항 $\frac{dx}{dt}$의 변화를 고려한다. 따라서 더 적은 샘플링 step을 허용하면서 더 높은 품질을 달성한다.

본 논문은 DDIM의 변형을 따라 RDM의 super-resolution 단계의 blurring diffusion에 EDM sampler를 적용한다. 이미지의 noisy한 상태 \(\{x_i\}_{i=0}^N\)에 대응하여 샘플링 step의 인덱스를 \(\{t_i\}_{i=0}^N\)으로 정의한다. Blurring diffusion을 적용하기 위해 이미지는 DCT에 의해 $u_i = V^\top x_i$로 주파수 공간으로 변환된다. DDIM은 inference 분포를 사용하여 diffusion process를 설명한다. 이를 blurring diffusion을 위해 다음과 같이 쓸 수 있다.

\[\begin{equation} q_\delta (u_{1:N} \vert u_0) = q_\delta (u_N \vert u_0) \prod_{n=2}^N q_\delta (u_{n-1} \vert u_n, u_0) \end{equation}\]

여기서 \(\delta \in \mathbb{R}_{\ge 0}^N\)은 분포에 대한 인덱스 벡터를 나타낸다. 모든 $n > 1$에 대해 reverse process는 다음과 같다.

\[\begin{equation} q_\delta (u_{n-1} \vert u_n, u_0) = \mathcal{N} (u_{n-1} \vert \frac{1}{\sigma_{t_n}} (\sqrt{\sigma_{t_{n-1}}^2 - \delta_n^2} u_n + (\sigma_{t_n} D_{t_{n-1}}^p - \sqrt{\sigma_{t_{n-1}}^2 - \delta_n^2} D_{t_n}^p) u_0), \delta_n^2 I) \end{equation}\]

정규 분포의 평균은 $q(u_n \vert u_0) = \mathcal{N} (u_n \vert D_{t_n}^p u_0, \sigma_{t_n}^2 I)$인 blurring diffusion 공식과 일치하도록 forward process를 보장한다. 인덱스 벡터 $\delta$가 0이면 sampler는 ODE sampler로 변환된다. 저자들은 sampler에 대해 $\delta_n = \eta \sigma_{t_{n−1}}$을 설정했다. 여기서 $\eta \in [0, 1)$는 샘플링 중에 주입된 랜덤성의 스케일을 제어하는 고정 스칼라이다. 이 정의를 위 식에 치환하면 sampler 함수를 다음과 같이 얻을 수 있다.

\[\begin{equation} u_{n-1} = (D_{t_{n-1}}^p + \gamma_n (I - D_{t_n}^p)) u_n + \sigma_{t_n} (\gamma_n D_{t_n}^p - D_{t_{n-1}}^p) \frac{u_n - \tilde{u}_0}{\sigma_{t_n}} + \eta \sigma_{t_{n-1}} \epsilon \\ \textrm{where} \quad \gamma_n = \sqrt{1 - \eta^2} \frac{\sigma_{t_{n-1}}}{\sigma_{t_n}} \end{equation}\]

Blurring diffusion 외에 block noise도 고려해야 하며, 단순히 Gaussian noise $\epsilon$을 block noise와 Gaussian noise의 가중 합인 $\tilde{\epsilon}$으로 대체하면 된다. \(\tilde{u}_0 = u_\theta (u_n, \sigma_{t_n})\)은 신경망에 의해 예측된다.

RDM의 super-resolution 단계에 대한 stochastic sampler는 Algorithm 1에 요약되어 있다.

Experiments

• 데이터셋: CelebA-HQ, ImageNet

1. Results

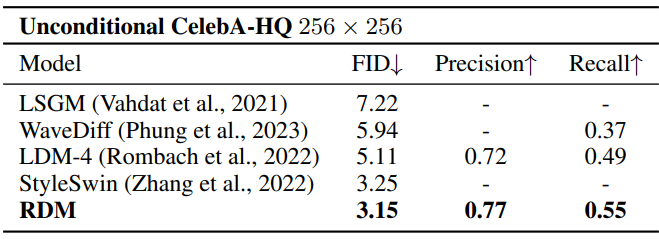
다음은 CelebA-HQ 256$\times$256에서 unconditional 이미지 생성 성능을 비교한 표이다.

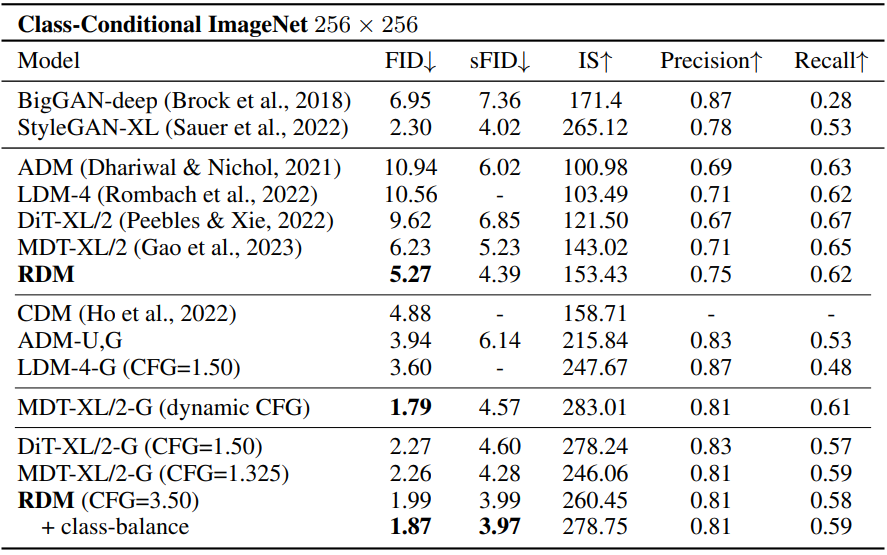
다음은 ImageNet 256$\times$256에서 클래스 조건부 이미지 생성 성능을 비교한 표이다.

2. Ablation Study

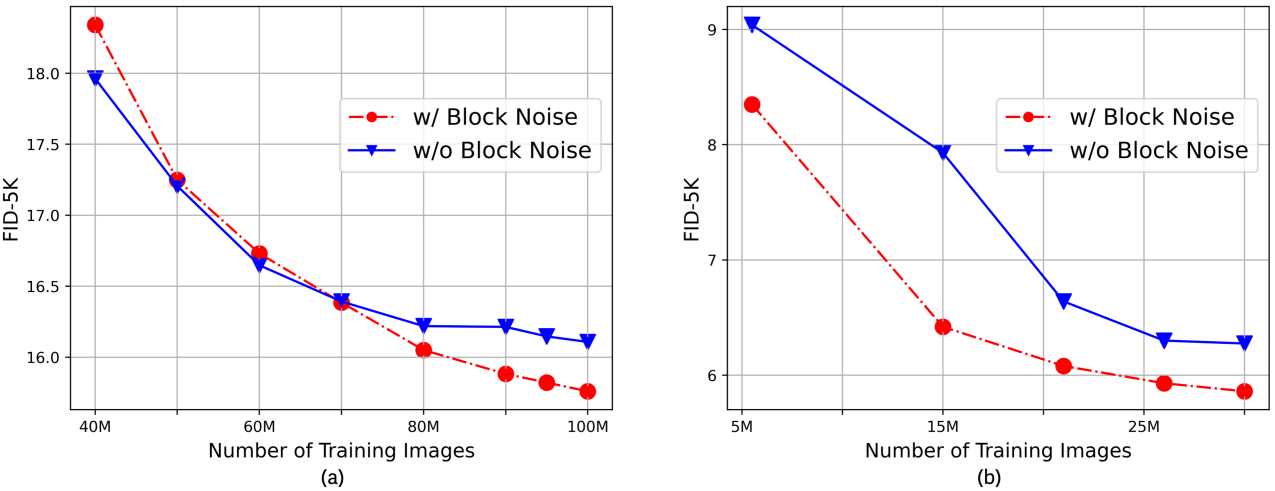
다음은 block noise의 유무에 따른 성능을 ImageNet 256$\times$256 (a)과 CelebA-HQ 256$\times$256 (b)에서 학습한 RDM으로 비교한 그래프이다. ($\alpha = 0.15$, $s = 4$)

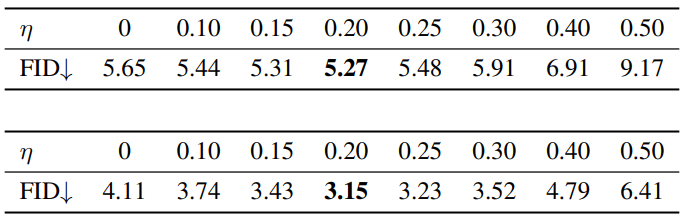
다음은 sampler의 stochasticity $\eta$에 따른 FID를 ImageNet 256$\times$256 (위)과 CelebA-HQ 256$\times$256 (아래)에서 비교한 표이다.

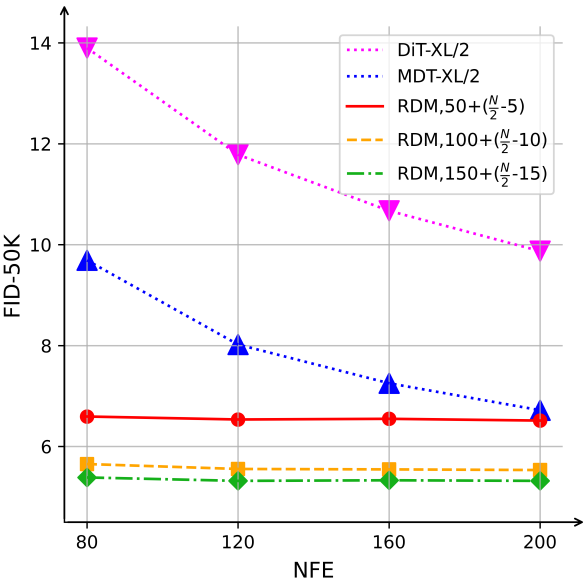
다음은 다양한 샘플링 step 수에 대한 FID를 ImageNet에서 비교한 그래프이다. $N$은 NFE이고, $10n+ (\frac{N}{2} −n)$은 첫 번째 단계에서 $10n$, 두 번째 단계에서 $\frac{N}{2} − n$을 의미한다.