[논문리뷰] Ref-NeRF: Structured View-Dependent Appearance for Neural Radiance Fields
CVPR 2022 (Oral). [Paper] [Page] [Github]
Dor Verbin, Peter Hedman, Ben Mildenhall, Todd Zickler, Jonathan T. Barron, Pratul P. Srinivasan
Harvard University | Google
7 Dec 2021

Introduction
NeRF는 새로운 시점에서 3D 장면의 사실적인 이미지를 렌더링한다. 장면의 입력 3D 좌표가 주어지면 spatial MLP는 해당 포인트에서 해당 volume density를 출력하고 directional MLP는 입력 viewing direction을 따라 해당 포인트에서 outgoing radiance를 출력한다. NeRF의 렌더링은 언뜻 타당해 보일 수 있지만 면밀히 검사하면 물리적으로 그럴듯한 방식으로 표면을 부드럽게 이동하는 대신 렌더링된 뷰 사이에서 페이드 인 및 페이드 아웃되는 허위 광택 아티팩트가 드러난다.
이러한 아티팩트는 NeRF의 두 가지 근본적인 문제로 인해 발생한다.
첫째, 각 포인트에서 outgoing radiance는 viewing direction의 함수이기 때문에 보간(interpolation)에 적합하지 않다. 아래 그림과 같이 단순한 예시의 경우에도 장면의 실제 radiance 함수가 viewing direction, 특히 specular highlight 주변에 따라 빠르게 변한다는 것을 보여준다. 결과적으로 NeRF는 학습 이미지에서 관찰된 특정 viewing direction에서만 정확하게 렌더링할 수 있으며 새로운 시점에서의 interpolation은 열악하다.
둘째, NeRF는 정반사(specular reflection)를 표현할 때 표면의 점에서 방출되는 view-dependent radiance 대신 물체 내부의 emitter를 사용하여 정반사를 위조하는 경향이 있다. 이 때문에 물체가 반투명하거나 흐린 껍질을 갖게 된다.
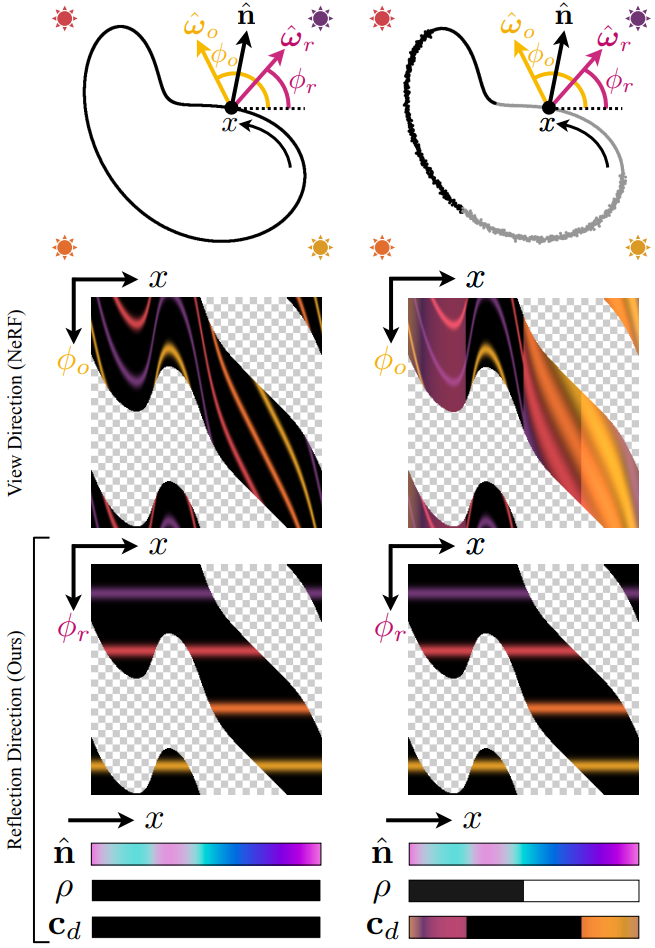
본 논문의 핵심 통찰력은 NeRF의 view-dependent 표현을 구조화하면 함수를 더 간단하고 보간하기 쉽게 만들 수 있다는 것이다. 본 논문은 viewing 벡터 대신 로컬 normal 벡터에 대한 viewing 벡터의 반사를 입력으로 하여 directional MLP를 reparameterize하는 Ref-NeRF라고 하는 모델을 제시하였다.
위 그림에서 볼 수 있듯이 이 reflected radiance가 표면 방향의 변화에 영향을 받지 않기 때문에 장면 전체에서 일정하다는 것을 보여준다. 결과적으로 directional MLP가 interpolation 커널 역할을 하기 때문에 Ref-NeRF는 가까운 점 사이의 외형 정보를 더 잘 공유하여 보간된 뷰에서 보다 현실적으로 렌더링할 수 있다.
또한 Integrated Directional Encoding (IDE)을 도입하고, outgoing radiance를 명시적인 diffuse 성분과 specular 성분으로 구조화하여 장면의 재료와 텍스처의 변화에도 reflected radiance 함수가 부드럽게 유지되도록 한다.
이러한 개선 사항을 통해 Ref-NeRF는 뷰에 따른 외형을 정확하게 보간할 수 있지만, 개선 사항들은 NeRF의 형상에서 추정된 normal 벡터에 의존한다. 이는 NeRF의 기하학적 구조가 흐리고 표면에 집중되어 있지 않으며 normal 벡터에 너무 잡음이 많아 반사 방향을 계산하는 데 유용하지 않기 때문에 문제가 된다. 저자들은 NeRF의 normal 벡터의 품질을 크게 향상시키고 volume density가 표면 주위에 집중되도록 장려하는 volume density에 대한 새로운 regularizer를 사용하여 이 문제를 개선하였다. 이를 통해 모델은 정확한 반사 벡터를 계산하고 사실적인 정반사를 렌더링할 수 있다.
저자들은 mip-NeRF에 이러한 변경 사항들을 적용하였다. Ref-NeRF는 새로운 시점의 SOTA 렌더링을 생성하고 반사성이 높거나 광택이 나는 물체에 대한 이전 SOTA 뷰 합성 방법의 품질을 크게 향상시켰다. 또한, outgoing radiance의 구조화는 설득력 있는 장면 편집 능력을 가능하게 하는 해석 가능한 성분 (normal 벡터, 거칠기, diffuse texture, specular tint)을 생성한다.
Structured View-Dependent Appearance

Ref-NeRF는 각 포인트에서 outgoing radiance를 들어오는 radiance, diffuse color, 거칠기, specular tint로 구조화한다. 이는 viewing direction에 따라 parameterize된 outgoing radiance보다 장면 전체의 부드러운 보간에 더 적합하다. Directional MLP에서 이러한 성분을 명시적으로 사용함으로써 Ref-NeRF는 specular highlight와 반사의 모양을 정확하게 재현할 수 있다. 또한, Ref-NeRF의 outgoing radiance의 분해를 통해 장면 편집이 가능하다.
1. Reflection Direction Parameterization
NeRF는 viewing direction을 직접 사용하는 반면, Ref-NeRF는 대신 로컬 normal 벡터에 대하여 반사된 viewing direction의 함수로 outgoing radiance를 reparameterize한다.
\[\begin{equation} \hat{\boldsymbol{\omega}}_r = 2 (\hat{\boldsymbol{\omega}}_o \cdot \hat{\mathbf{n}}) \hat{\mathbf{n}} - \hat{\boldsymbol{\omega}}_o \end{equation}\]여기서 \(\hat{\boldsymbol{\omega}}_o = - \hat{\mathbf{d}}\)는 공간의 한 포인트에서 카메라를 가리키는 단위 벡터이고, $\hat{\mathbf{n}}$는 해당 포인트의 normal 벡터이다. 이러한 reparameterization은 specular 모양을 보간에 더 적합하게 만든다.
반사된 viewing direction에 대해 회전 대칭인 BRDF의 경우, 즉 일부 lobe function $p$에 대해 \(f(\hat{\boldsymbol{\omega}}_i, \hat{\boldsymbol{\omega}}_o) = p(\hat{\boldsymbol{\omega}}_r \cdot \hat{\boldsymbol{\omega}}_i)\)를 충족하고 interreflection이나 self-occlusion과 같은 현상을 무시한 BRDF의 경우, view-dependent radiance는 반사 방향 \(\hat{\boldsymbol{\omega}}_r\)만의 함수이다.
\[\begin{equation} L_\textrm{out} (\hat{\boldsymbol{\omega}}_o) \propto \int L_\textrm{in} (\hat{\boldsymbol{\omega}}_i) p(\hat{\boldsymbol{\omega}}_r \cdot \hat{\boldsymbol{\omega}}_i) d \hat{\boldsymbol{\omega}}_i = F (\hat{\boldsymbol{\omega}}_r) \end{equation}\]따라서 반사 방향으로 directional MLP를 쿼리함으로써 \(\hat{\boldsymbol{\omega}}_r\)의 함수로 이 적분을 출력하도록 학습시킨다. 보다 일반적인 BRDF는 프레넬 효과(Fresnel Effect)와 같은 현상으로 인해 viewing direction과 normal 벡터 사이의 각도에 따라 달라질 수 있으므로 directional MLP에 \(\hat{\mathbf{n}} \cdot \hat{\boldsymbol{\omega}}_o\)도 입력한다.
2. Integrated Directional Encoding
공간적으로 변화하는 재료가 포함된 현실적인 장면에서 radiance는 반사 방향만의 함수로 표현될 수 없다. 거친 재료의 모양은 반사 방향에 따라 천천히 변하는 반면, 매끄럽거나 반짝이는 재료의 모양은 빠르게 변한다. 저자들은 directional MLP가 연속적인 거칠기를 갖는 재료의 outgoing radiance의 함수를 효율적으로 표현할 수 있도록 하기 위해 Integrated Directional Encoding (IDE)을 도입하였다. IDE는 mip-NeRF의 integrated positional encoding에서 영감을 받았다.
먼저, NeRF에서 수행된 것처럼 sinusoidal 집합으로 방향을 인코딩하는 대신 spherical harmonic의 집합 \(\{Y_\ell^m\}\)으로 방향을 인코딩한다. 이 인코딩은 구에 고정되어 있다는 이점을 제공하며, 이는 유클리드 공간에서의 위치 인코딩의 효율성에 중요하다.
다음으로 하나의 벡터 대신 반사 벡터 분포를 인코딩하여 거칠기가 다른 재료에 대해 추론할 수 있는 directional MLP를 활성화한다. von Mises-Fisher (vMF) 분포 (정규화된 구형 가우시안)를 사용하여 단위 구에 정의된 이 분포를 반사 벡터 \(\hat{\boldsymbol{\omega}}_r\)을 중심으로 하고 $\kappa = 1/\rho$로 정의된 concentration parameter $\kappa$를 사용하여 모델링한다. 거칠기 $\rho$는 spatial MLP에서 출력되고 표면의 거칠기를 결정한다. $\rho$ 값이 클수록 vMF 분포에서 더 넓은 거친 표면을 표현한다. IDE는 이 vMF 분포에서 spherical harmonic 집합의 기댓값을 사용하여 반사 방향 분포를 인코딩한다.
\[\begin{equation} \textrm{IDE} (\hat{\boldsymbol{\omega}}_r, \kappa) = \{ \mathbb{E}_{\hat{\boldsymbol{\omega}} \sim \textrm{vMF} (\hat{\boldsymbol{\omega}}_r, \kappa)} [Y_\ell^m (\hat{\boldsymbol{\omega}})] : (\ell, m) \in \mathcal{M}_L \} \\ \mathcal{M}_L = \{ (\ell, m) : \ell = 1, \ldots, 2^L, m = 0, \ldots, \ell \} \end{equation}\]vMF 분포에서 spherical harmonic의 기대값은 다음과 같은 간단한 closed-form 표현을 가진다.
\[\begin{equation} \mathbb{E}_{\hat{\boldsymbol{\omega}} \sim \textrm{vMF} (\hat{\boldsymbol{\omega}}_r, \kappa)} [Y_\ell^m (\hat{\boldsymbol{\omega}})] = A_\ell (\kappa) Y_\ell^m (\hat{\boldsymbol{\omega}}_r) \end{equation}\]그리고 $\ell$번째 감쇠 함수 $A_\ell (\kappa)$는 간단한 지수 함수를 사용하여 잘 근사될 수 있다.
\[\begin{equation} A_\ell (\kappa) \approx \exp \bigg( - \frac{\ell (\ell+1)}{2 \kappa} \bigg) \end{equation}\]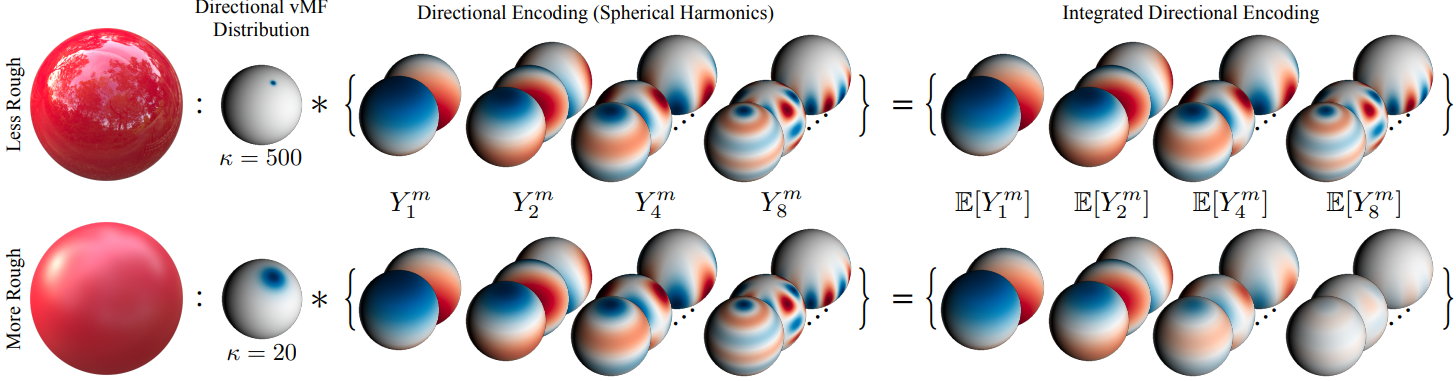
위 그림은 IDE가 직관적임을 보여준다. $\kappa$를 낮춰 재료의 거칠기를 증가시키는 것은 IDE의 spherical harmonics를 높은 차수 $\ell$로 감쇠시키는 것에 해당하며, 그 결과 view-dependent color의 고주파수를 제한하는 더 넓은 interpolation 커널이 생성된다.
3. Diffuse and Specular Colors
Diffuse color가 위치만의 함수라는 사실을 사용하여 diffuse 성분과 specular 성분을 분리함으로써 outgoing radiance의 함수를 더욱 단순화한다. Spatial MLP를 수정하여 diffuse color \(\mathbf{c}_d\)와 specular tint \(\mathbf{s}\)를 출력하고 이를 directional MLP에서 제공하는 specular color \(\mathbf{c}_s\)와 결합하여 하나의 색상 값을 얻는다.
\[\begin{equation} \mathbf{c} = \gamma (\mathbf{c}_d + s \odot \mathbf{c}_s) \end{equation}\]여기서 $\odot$은 element-wise multiplication이며 $\gamma$는 선형 색상을 sRGB로 변환하고 출력 색상을 $[0, 1]$에 놓이도록 clip하는 고정된 tone mapping 함수이다.
4. Additional Degrees of Freedom
조명의 interreflection이나 self-occlusion과 같은 효과로 인해 조명이 장면 전체에 걸쳐 공간적으로 다양해진다. 따라서 spatial MLP에 의해 출력된 bottleneck 벡터 $\mathbf{b}$를 directional MLP에 추가로 전달하여 reflected radiance가 3D 위치에 따라 변경될 수 있도록 한다.
Accurate Normal Vectors
앞서 설명한 outgoing radiance의 구조화는 반사광 보간을 위한 더 나은 parameterization을 제공하지만 정확한 반사 방향 벡터를 위해서는 volume density의 좋은 추정에 의존한다. 그러나 NeRF 기반 모델에 의해 복구된 volume density는 두 가지 제한 사항을 안고 있다.
- Volume density 기울기에서 추정된 normal 벡터는 종종 극도로 잡음이 많다.
- NeRF는 specular highlight를 만들기 위해 diffuse 표면 아래에 emitter를 넣어 가짜로 만드는 경향이 있다. 이는 diffuse 표면이 반투명해지기 때문에 최선이 아니다.
저자들은 반사 방향을 계산하기 위해 normal을 예측하여 첫 번째 문제를 해결하였다. 광선을 따라 각 위치 \(\mathbf{x}_i\)에 대해 spatial MLP에서 3-벡터를 출력한 다음 이를 정규화하여 normal 예측 \(\hat{\mathbf{n}}_i^\prime\)을 얻는다. 이러한 예측된 normal을 간단한 페널티를 사용하여 각 광선상의 밀도 기울기 normal 샘플 \(\{\hat{\mathbf{n}}_i\}\)와 일치시킨다.
\[\begin{equation} \mathcal{R}_\textrm{p} = \sum_i w_i \| \hat{\mathbf{n}}_i - \hat{\mathbf{n}}_i^\prime \|^2 \end{equation}\]여기서 $w_i$는 광선상의 $i$번째 샘플의 가중치이다. \(\hat{\mathbf{n}}_i^\prime\)은 기울기 연산자가 MLP의 interpolation 커널에서 high-pass filter 역할을 하기 때문에 \(\{\hat{\mathbf{n}}_i\}\)보다 더 부드러운 경향이 있다.
저자들은 렌더링된 색상에 기여하는 광선상의 샘플에서 뒤쪽을 향하는, 즉 카메라에서 멀어지는 방향의 normal에 불이익을 주는 새로운 정규화 항을 도입하여 두 번째 문제를 해결하였다.
\[\begin{equation} \mathcal{R}_\textrm{o} = \sum_i w_i \, \textrm{max} (0, \hat{\mathbf{n}}_i^\prime \cdot \hat{\mathbf{d}})^2 \end{equation}\]이 정규화는 흐린 표면에 대한 페널티 역할을 한다. 샘플은 가시적이고 (높은 $w_i$) volume density가 광선을 따라 감소할 때 (내적이 양수) 페널티를 받는다. 이러한 페널티로 인해 Ref-NeRF는 반사광을 반투명 표면 아래에 숨겨진 emitter로 설명하는 것을 방지하고 결과적으로 향상된 normal을 통해 directional MLP를 쿼리하는 데 사용할 정확한 반사 방향을 계산할 수 있다.
Experiments
- 구현 디테일: mip-NeRF 위에 구현
- 동일한 spatial MLP (레이어 8개, hidden unit 256개, ReLU)
- 더 큰 directional MLP (레이어 8개, hidden unit 256개, ReLU)
Shiny Blender Dataset
NeRF에서 사용하는 Blender 데이터셋에는 복잡한 형상을 가진 다양한 개체가 포함되어 있지만 재료의 다양성 측면에서 심각하게 제한되어 있으며 대부분의 장면은 거의 Lambertian이다. 보다 까다로운 재료 특성을 조사하기 위해 저자들은 NeRF의 데이터셋과 유사한 조건 (장면당 학습 이미지 100개, 테스트 이미지 200개)에서 Blender에서 렌더링된 6개의 서로 다른 광택이 있는 개체가 포함된 Shiny Blender 데이터셋을 만들었다.
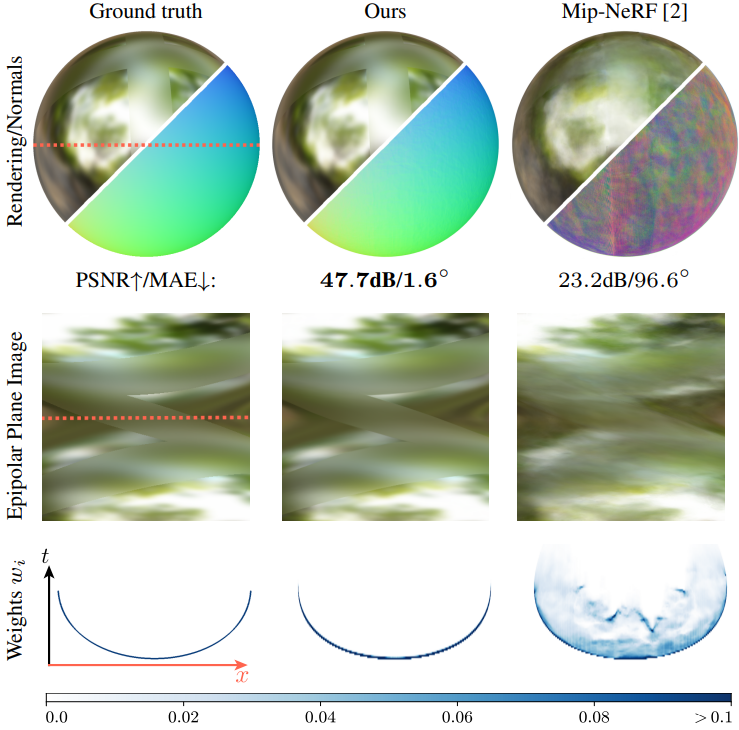
다음은 Shiny Blender 데이터셋에서 반사가 강한 장면에 대하여 Ref-NeRF를 mip-NeRF와 비교한 결과이다.

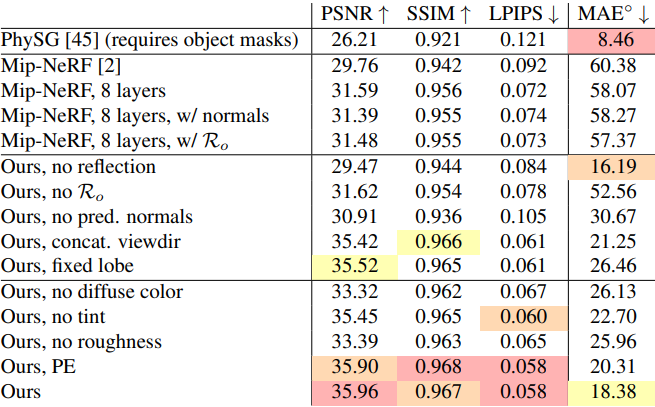
다음은 Shiny Blender 데이터셋에서 최근 뷰 합성 방법들과 비교한 결과이다.
Blender Dataset
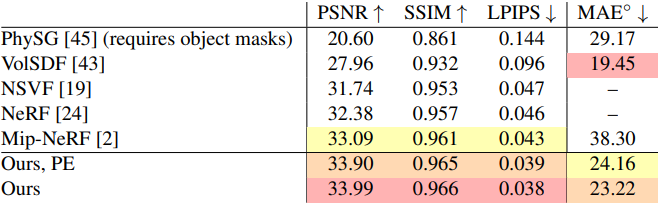
다음은 NeRF 논문의 Blender 데이터셋에서 최근 뷰 합성 방법들과 비교한 결과이다.

Real Captured Scenes
다음은 실제 장면에 대한 결과이다.

Scene Editing
다음은 장면 성분의 편집 예시이다.

Limitations
- 이전 방법들보다 더 많은 계산이 필요하다. IDE를 평가하는 것은 위치 인코딩을 계산하는 것보다 약간 느리고, normal 벡터를 계산하기 위해 spatial MLP의 기울기를 통해 역전파하는 것은 mip-NeRF보다 약 25% 느려진다.
- 반사 방향에 따른 outgoing radiance의 reparameterization은 interreflection이나 가까운 조명을 명시적으로 모델링하지 않으므로 이러한 경우 mip-NeRF에 대한 개선이 줄어든다.