[논문리뷰] Rectified Point Flow: Generic Point Cloud Pose Estimation
NeurIPS 2025 (Spotlight). [Paper] [Page] [Github]
Tao Sun, Liyuan Zhu, Shengyu Huang, Shuran Song, Iro Armeni
Stanford University | NVIDIA Research
5 Jun 2025
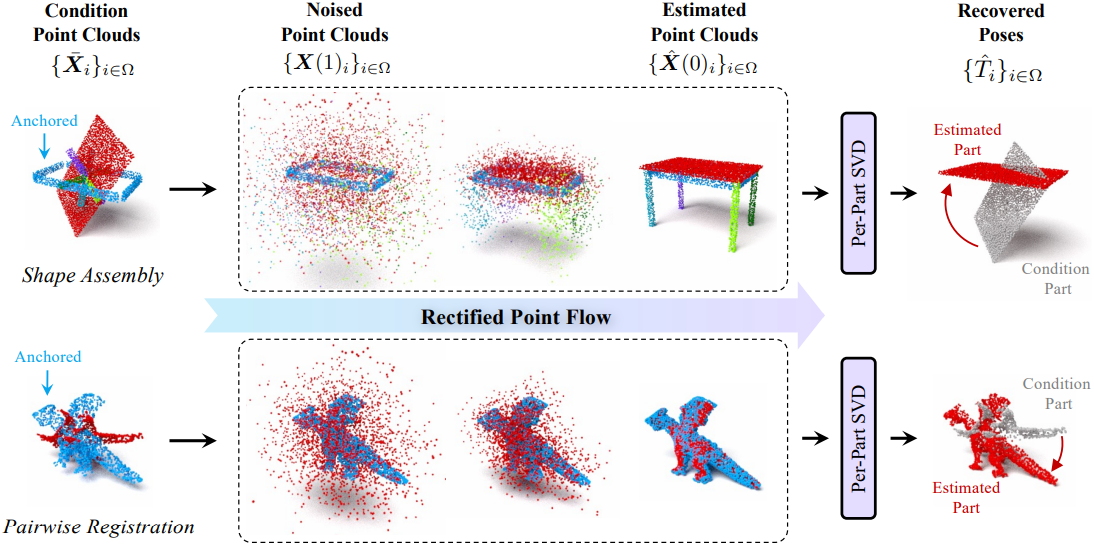
Introduction
Multi-part shape 조립은 본질적으로 제약이 부족하다. Part들은 종종 대칭적이거나, 상호 교환 가능하거나, 기하학적으로 모호하여 여러 가지 그럴듯한 로컬 구성이 발생한다. 결과적으로, 기존의 part별 registration은 로컬하게는 유효하지만 의도된 조립과 전체적으로는 일치하지 않는 뒤집히거나 정렬되지 않은 구성을 생성할 수 있다. 이러한 모호성을 극복하려면 강력한 supervision이나 휴리스틱에 의존하지 않고도 부품의 동일성, 상대적 배치, 그리고 전체적인 shape 일관성에 대해 공동으로 추론할 수 있는 모델이 필요하다.
본 논문에서는 입력 geometry에 대한 연속적인 point-wise flow field을 학습하는 문제를 일반적인 포인트 클라우드 포즈 추정을 위한 생성적 접근법으로 제시하며, 이를 통해 조립된 shape들에 대한 prior를 효과적으로 포착한다. 본 논문에서 제안하는 Rectified Point Flow는 유클리드 공간에서 랜덤 Gaussian noise로부터 조립된 object들의 포인트 클라우드를 향해 이동하는 점들의 움직임을 모델링한다. 이렇게 학습된 flow는 part-level transformation을 암묵적으로 인코딩하여 하나의 프레임워크 내에서 포즈 추정과 생성적 shape 조립을 모두 가능하게 한다. Rectified Point Flow는 점별 feature를 추출하는 인코더와, 주어진 feature를 기반으로 최종 조립 위치를 예측하는 flow model로 구성된다.
Part 간 관계에 대한 기하학적 인식을 심어주기 위해, 저자들은 대규모 3D shape 데이터셋을 사용하여 인코더를 사전 학습시켰다. 구체적으로, binary classification task로써 각 점마다 part 간 중첩을 예측한다. 다양한 task에 맞춰진 데이터 소스에 구애받지 않고 데이터를 생성할 수 있으며, 완벽한 메쉬나 시뮬레이션을 필요로 하지 않는다. 이는 포즈 추정을 위한 scalable한 사전 학습을 향한 중요한 단계이다.
본 논문의 flow 기반 포즈 추정은 세 가지 측면에서 기존의 포즈 벡터 추정과 다르다.
- Shape-포즈 공동 추론: 완전한 shape을 재구성하는 동시에 part 포즈 추정을 가능하게 한다.
- Scalable한 shape 사전 학습: 최종 조립된 포인트 클라우드를 예측하도록 학습함으로써, 모델은 다양한 데이터셋과 part 정의로부터 학습할 수 있으며, scalable한 학습이 가능하다.
- 내재적 대칭 처리: SE(3) 공간에서 포즈 벡터를 직접 예측하는 대신, 포인트 클라우드에 대한 유클리드 공간에서 작업한다. 이를 통해 모델은 대칭, part 상호 교환성, 공간적 모호성에 본질적으로 robust하다.
Pose Estimation via Rectified Point Flow
1. Problem Definition
여러 object part로 구성된 포인트 클라우드 집합 \(\{\textbf{X}_i \in \mathbb{R}^{3 \times N_i}\}_{i \in \Omega}\)를 고려하자 ($\Omega$는 part 인덱스 집합). 목표는 $\textbf{X}$의 각 part를 정렬하여 글로벌 좌표계에서 하나의 조립된 object $\textbf{Y}$를 형성하는 rigid transformation 집합 \(\{T_i \in \textrm{SE}(3)\}_{i \in \Omega}\)을 구하는 것이다.
\[\begin{equation} \textbf{X} = \bigcup_{i \in \Omega} \textbf{X}_i \in \mathbb{R}^{3 \times N}, \quad \textbf{Y} = \bigcup_{i \in \Omega} T_i \textbf{X}_i \in \mathbb{R}^{3 \times N}, \quad N = \sum_{i \in \Omega} N_i \end{equation}\]글로벌 translation 및 rotation 모호성을 제거하기 위해 첫 번째 part($i = 0$)를 앵커로 설정하고 해당 앵커의 좌표계를 글로벌 좌표계로 정의한다.
2. Overlap-aware Point Encoding

포즈 추정은 연결된 part 간의 서로 겹치는 영역에서 나오는 기하학적 단서에 의존한다. 본 논문에서는 pose-invariant point feature를 생성할 수 있는 task 독립적인 overlap-aware encoder를 사전 학습시켰다. 위 그림에서 볼 수 있듯이, 서로 다른 part에서 겹치는 점을 식별하도록 인코더 $F$를 학습시킨다. 주어진 part 집합 \(\{\textbf{X}_i\}_{i \in \Omega}\)에 대하여, 먼저 임의의 rigid transformation \(\tilde{T}_i \in \textrm{SE}(3)\)을 적용하고 변환된 포인트 클라우드 \(\tilde{\textbf{X}}_i = \tilde{T}_i \textbf{X}_i\)를 인코더에 대한 입력으로 구성한다. 이러한 data augmentation을 통해 인코더는 더욱 robust한 pose-invariant feature를 학습할 수 있다. 그런 다음 인코더는 part $i$의 $j$번째 점에 대해 point feature \(C_{i,j} \in \mathbb{R}^d\)를 계산한 후 overlap head (MLP)가 겹침 확률 \(\hat{p}_{i,j}\)를 추정한다. 바이너리 GT 레이블 $p_{i,j}$는 점 \(\tilde{\textbf{x}}_{i,j}\)가 다른 part의 적어도 한 점의 반경 $\epsilon$ 내에 있는 경우 1이다.
인코더와 overlap head를 모두 binary cross-entropy loss를 사용하여 학습시킨다. 미리 정의된 part segmentation이 없는 object의 경우, 기존 3D part segmentation 방법을 사용하여 필요한 레이블을 생성한다. 학습된 인코더에서 추출된 feature는 이후 Rectified Point Flow 모델의 컨디셔닝 입력으로 사용된다.
3. Generative Modeling for Pose Estimation
Overlap-aware encoder는 part 간의 잠재적 중첩 영역을 식별하지만, 특히 여러 개의 유효한 조립 구성을 허용하는 대칭 object의 경우 최종 정렬을 결정할 수는 없다. 이러한 한계를 해결하기 위해, 저자들은 포인트 클라우드 포즈 추정을 조건부 생성 문제로 재구성했다. 이 접근 방식을 통해 Rectified Point Flow는 추출된 point feature를 활용하여 모든 가능한 조립 상태의 조건부 분포를 샘플링하여 입력 포인트 클라우드의 likelihood를 최대화하는 추정치를 생성한다. 포즈 추정을 생성 문제로 재구성함으로써, 데이터의 대칭성과 part 호환성으로 인해 발생하는 내재적인 모호성을 자연스럽게 수용할 수 있다.
Preliminaries
Rectified Flow (RF)는 소스 분포의 샘플 $\textbf{X}(0)$를 타겟 분포의 $\textbf{X}(1)$로 변환하는 방법을 학습하는 생성 모델링 프레임워크이다. Forward process는 timestep $t$를 사용한 두 샘플 간의 linear interpolation으로 정의된다.
\[\begin{equation} \textbf{X}(t) = (1-t) \textbf{X}(0) + t \textbf{X}(1), \quad t \in [0, 1] \end{equation}\]Reverse process는 velocity field \(\nabla_t \textbf{X}(t)\)로 모델링되며, 이는 conditional flow matching (CFM) loss를 사용하여 학습되는 네트워크 \(\textbf{V}(t, \textbf{X}(t) \,\vert\, \textbf{X})\)로 parameterize된다.
\[\begin{equation} \mathcal{L}_\textrm{CFM}(\textbf{V}) = \mathbb{E}_{t, \textbf{X}} [\| \textbf{V} (t, \textbf{X}(t) \,\vert\, \textbf{X}) - \nabla_t \textbf{X}(t) \|^2] \end{equation}\]Rectified Point Flow
본 논문에서는 포인트 클라우드들의 3D 유클리드 좌표에 RF를 직접 적용하였다. Part $i$에서 샘플링된 $M_i$개의 점에 대하여, \(\textbf{X}_i (t) \in \mathbb{R}^{3 \times M_i}\)를 timestep $t$에서의 포인트 클라우드라 하자. $t = 0$에서 \(\{\textbf{X}_i (0)\}_{i \in \Omega}\)는 조립된 object $\textbf{Y}$에서 균일하게 샘플링되는 반면, $t = 1$에서 각 part의 점은 Gaussian $\mathcal{N}(0,I)$에서 독립적으로 샘플링된다.
그런 다음, 각 part에 대한 continuous flow를 noise가 있는 상태의 점과 조립된 상태의 점 사이의 3D 유클리드 공간에서 직선 interpolation으로 정의한다.
\[\begin{equation} \textbf{X}_i (t) = (1 - t) \textbf{X}_i (0) + t \textbf{X}_i (1), \quad t \in [0, 1] \end{equation}\]따라서 Rectified Point Flow의 velocity field는 다음과 같다.
\[\begin{equation} \frac{\textrm{d} \textbf{X}_i (t)}{\textrm{d} t} = \textbf{X}_i (1) - \textbf{X}_i (0) \end{equation}\]고정된 part($i = 0$)는 모든 $t \in [0, 1]$에 대해 \(\textbf{X}_0 (t) = \textbf{X}_0 (0)\)으로 설정한다. 이는 해당 점들의 속도를 0으로 만드는 마스크를 통해 구현된다. 모델이 각 부분 \(\hat{\textbf{X}}_i (0)\)의 조립된 포인트 클라우드를 예측하면, 해당 part의 포즈 $T_i$를 복구한다 (Procrustes problem).
\[\begin{equation} \hat{T}_i = \underset{\hat{T}_i \in \textrm{SE}(3)}{\arg \min} \| \hat{T}_i \textbf{X}_i - \hat{\textbf{X}}_i (0) \|_F \end{equation}\]SVD를 통해 고정되지 않은 모든 part들에 대한 포즈 \(\hat{T}_i\)를 풀면 포즈 추정이 완료된다.
Learning Objective
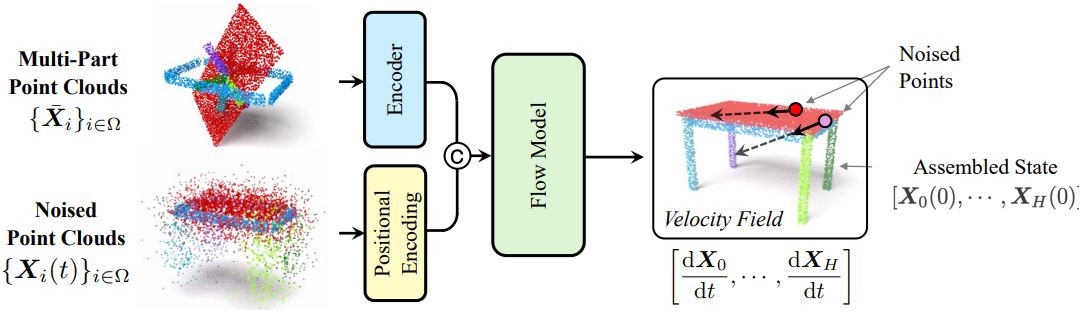
위 그림과 같이, noise가 적용된 포인트 클라우드 \(\{\textbf{X}_i (t)\}_{i \in \Omega}\)을 입력받고, \(\textbf{X}\)를 조건으로 하여 velocity field를 복원하는 flow model $V$를 학습시킨다. 먼저, 사전 학습된 인코더 $F$를 사용하여 $\textbf{X}$를 인코딩한다. 각 noise가 적용된 포인트 클라우드에 대해 3차원 좌표와 part 인덱스에 위치 인코딩을 적용하고, 이러한 임베딩을 point feature와 concat하여 결과를 flow model에 입력한다. 모든 점에 대하여 flow model에 의해 예측된 velocity field를 구하고, CFM loss로 flow model $V$를 최적화한다.
Experiments
- 구현 디테일
- 포인트 클라우드 인코더 backbone: PointTransformerV3 (PTv3)
- Flow model: Diffusion Transformer (DiT)
- 각 layer는 part별 self-attention과 모든 part에 대한 글로벌 self-attention을 수행
- GPU: NVIDIA A100 80GB 8개
- iteration: 40만
- effective batch size: 256
- optimizer: AdamW
- learning rate: $5 \times 10^{-4}$
- 처음 27.5만 iteration 후 2.5만 iteration마다 절반
학습에 사용된 데이터셋은 다음과 같다.
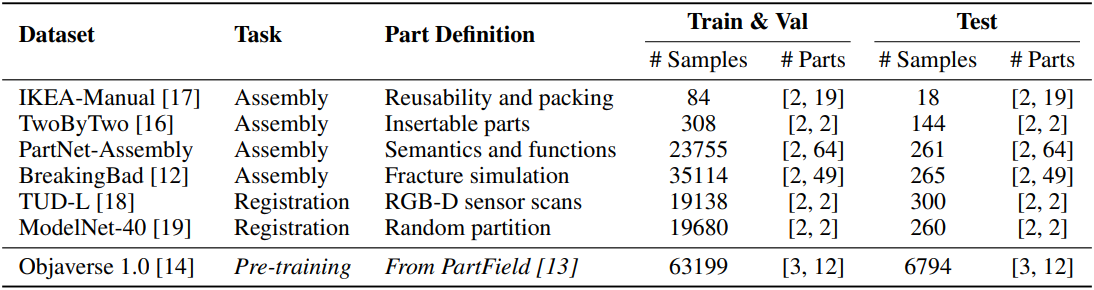
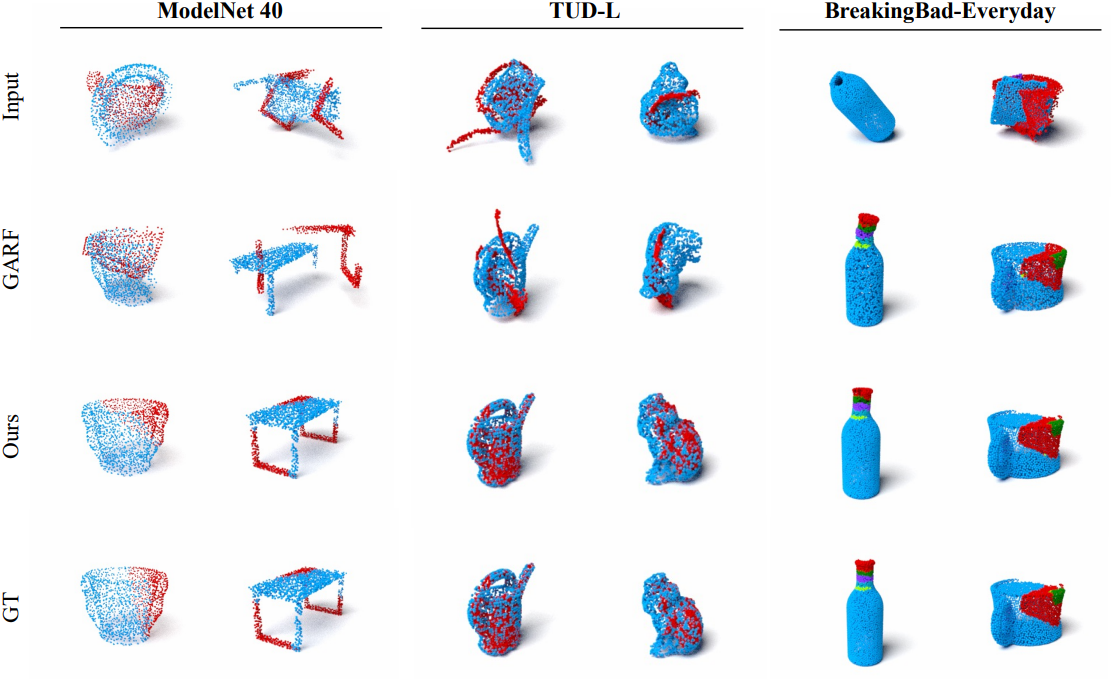
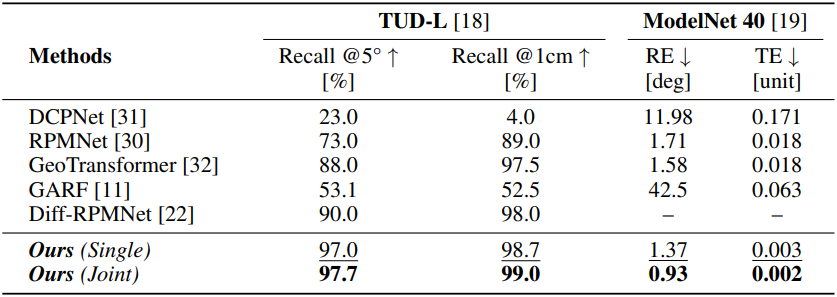
다음은 여러 part에 대한 조립 성능을 비교한 결과이다.

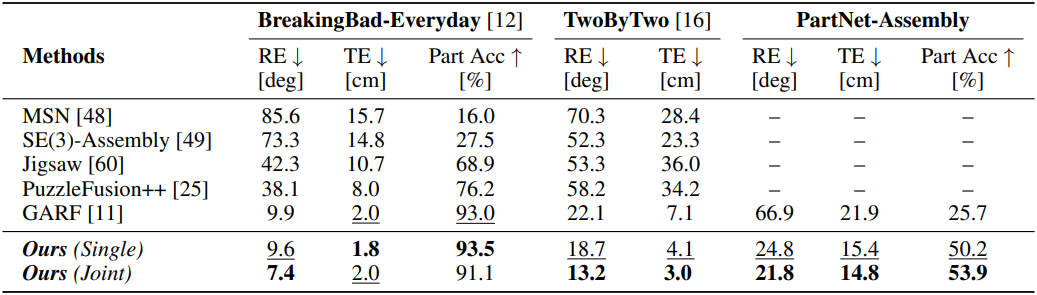
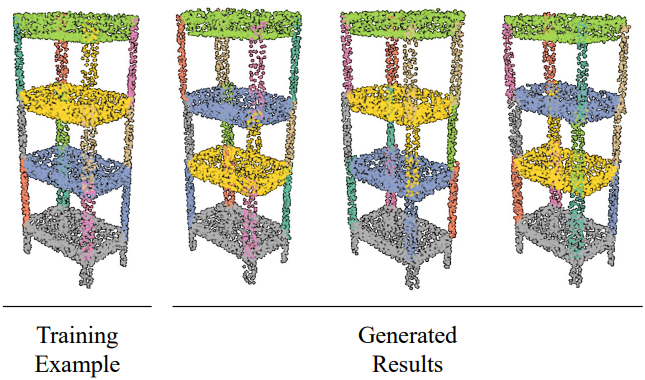
다음은 대칭적인 part에 대한 조립 예시이다.
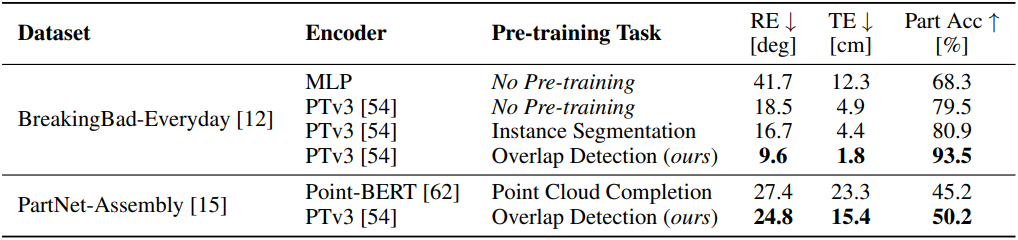
다음은 인코더 사전 학습에 대한 ablation 결과이다.
Limitations
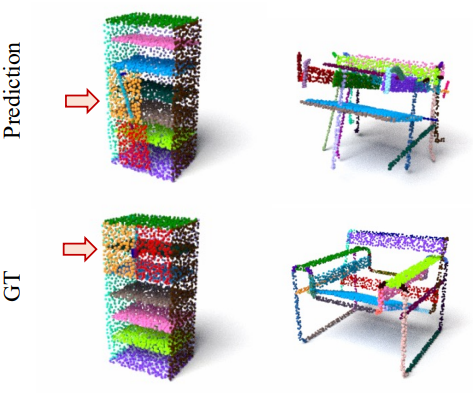
- 여러 가지 타당한 조립 결과를 생성할 수 있지만, 그중 일부는 기계적으로 기능하지 않을 수 있다.
- 특정 기하학적 복잡성을 초과하는 object를 처리할 수 없다.
- 모델이 처리할 수 있는 포인트 수에 한계가 있으며, 이는 대규모 object에 대한 사용을 제한한다.