[논문리뷰] RealFusion: 360° Reconstruction of Any Object from a Single Image

CVPR 2023. [Paper] [Page] [Github]
Luke Melas-Kyriazi, Christian Rupprecht, Iro Laina, Andrea Vedaldi
University of Oxford
21 Feb 2023

Introduction

본 논문은 단일 이미지가 주어진 어떤 물체의 360도 사진 재구성을 얻는 문제를 고려한다. 문제는 단일 이미지에 3D 재구성을 위한 충분한 정보가 포함되어 있지 않다는 것이다. 여러 시점에 액세스할 수 없으면 이미지는 개체의 3D 모양에 대한 약한 증거만 제공하고 개체의 한 면에 대해서만 제공한다. 그럼에도 불구하고 이 task를 해결할 수 있다는 증거가 있다. 숙련된 3D 아티스트라면 거의 모든 개체의 사진을 찍을 수 있고 충분한 시간과 노력이 주어지면 그럴듯한 3D 모델을 만들 수 있다. 작가는 자연 세계와 그 안에 포함된 사물에 대한 방대한 지식을 활용하여 이미지에서 누락된 정보를 보충함으로써 그렇게 할 수 있다.

이 문제를 알고리즘적으로 해결하려면 시각적 형상을 3D 세계의 강력한 통계 모델과 결합해야 한다. 최근 DALL-E, Imagen, Stable Diffusion과 같은 2D 이미지 generator의 폭발적인 증가는 그러한 모델이 그리 뒤지지 않을 수 있음을 시사한다. 이러한 방법들은 diffusion을 사용하여 매우 모호한 생성 task를 해결할 수 있으며 텍스트 설명, semantic map, 부분적으로 완료된 이미지, 단순히 랜덤 noise로부터 그럴듯한 2D 이미지를 얻을 수 있다. 분명히, 이러한 모델은 3D 세계가 아니라면 적어도 2D 이미지에서 표현되는 방식의 고품질 prior(사전 지식)를 가지고 있다. 따라서 이론적으로 방대한 양의 3D 데이터에 대해 학습된 3D diffusion model은 unconditional하게 또는 2D 이미지를 조건으로 하여 3D 재구성을 생성할 수 있어야 한다. 그러나 그러한 모델을 학습하는 것은 불가능하다. 수십억 개의 2D 이미지에 액세스할 수 있지만 3D 데이터에 대해서는 그렇지 않기 때문이다.

3D diffusion model 학습의 대안은 기존 2D 모델에서 3D 정보를 추출하는 것이다. 2D 이미지 generator는 실제로 주어진 개체의 여러 view를 샘플링하거나 검증하는 데 사용할 수 있다. 그런 다음 이러한 여러 view를 사용하여 3D 재구성을 수행할 수 있다. 몇몇 연구들은 초기 GAN 기반 generator를 사용하여 얼굴 및 합성 개체와 같은 간단한 데이터에 대해 어느 정도 성공을 거두었다. CLIP과 같은 대규모 모델과 최근 diffusion model의 가용성으로 점점 더 복잡한 결과를 얻었다. 가장 최근의 예는 텍스트 설명만으로 고품질 3D 모델을 생성하는 DreamFusion이다.

이러한 발전에도 불구하고 단일 이미지 3D 재구성 문제는 대부분 해결되지 않은 상태로 남아 있다. 사실, 이러한 최근의 방법들은 이 문제를 해결하지 못한다. 임의의 개체를 샘플링하거나 DreamFusion의 경우와 같이 텍스트 설명에서 시작한다.

Generator를 재구성으로 확장할 때의 문제는 적용 범위이다 (mode collapse라고도 함). 예를 들어 GAN을 기반으로 하는 고품질 얼굴 generator는 일반적으로 반전하기 어렵다. 다양한 고품질 이미지를 생성할 수 있지만 일반적으로 대부분의 이미지를 생성할 수는 없다. 이미지에 대한 컨디셔닝은 텍스트 설명보다 개체에 대한 훨씬 더 자세하고 미묘한 사양을 제공한다. Generator 모델이 이러한 모든 제약 조건을 충족할 수 있는지는 확실하지 않다.

본 논문에서는 diffusion model의 맥락에서 이 문제를 연구한다. 저자들은는 neural radiance field (NeRF)를 통해 물체의 3D 형상과 외관을 표현한다. 그런 다음 일반적인 렌더링 loss를 최소화하여 주어진 입력 이미지를 재구성하도록 radiance field를 학습한다. 동시에 객체의 임의의 다른 view를 샘플링하고 DreamFusion과 유사한 기술을 사용하여 diffusion prior로 제한한다.

저자들은 기본적으로 이 아이디어가 잘 작동하지 않는다는 것을 알게 되었다. 대신 많은 개선과 수정이 필요하다. 가장 중요한 변화는 diffusion model을 적절하게 컨디셔닝하는 것이다. 아이디어는 주어진 객체의 다른 view를 그럴듯하게 구성할 수 있는 “dream up” 또는 샘플 이미지의 prior를 구성하는 것이다. 주어진 이미지의 랜덤 augmentation에서 diffusion 프롬프트를 엔지니어링하여 이를 수행한다. 이러한 방식으로만 diffusion model이 의미 있는 3D 재구성을 허용하기에 충분히 강력한 제약 조건을 제공한다.

프롬프트를 올바르게 설정하는 것 외에도 기본 형상을 음영 처리하고 텍스처를 임의로 삭제(DreamFusion과 유사)하고 표면의 법선을 매끄럽게 하고 coarse-to-fine 방식으로 모델을 맞추는 정규화 도구도 추가한다. 먼저 개체의 전체 구조를 캡처한 다음 세밀한 디테일만 캡처한다. 또한 효율성에 중점을 두고 InstantNGP에 모델을 기반으로 한다. 이러한 방식으로 기존의 MLP 기반 NeRF 모델을 채택하는 경우 며칠이 아닌 몇 시간 안에 재구성을 달성한다.

저자들은 랜덤 이미지와 기존 벤치마크 데이터셋을 사용하여 접근 방식을 평가하였다. 완전한 2D-to-3D 모델을 학습하지 않으며 특정 개체 카테고리로 제한되지 않는다. 오히려 사전 학습된 2D generator를 prior로 사용하여 이미지별로 재구성을 수행한다. 그럼에도 불구하고 Shelf-Supervised Mesh Prediction을 포함하여 양적 및 질적으로 이전의 단일 이미지 reconstructor를 능가할 수 있다.

더 인상적이며 더 중요한 것은 제공된 입력 이미지와 잘 일치하는 그럴듯한 3D 재구성을 얻는다는 점이다. Diffusion prior가 사용 가능한 이미지 증거를 설명하기 위해 최선을 다하지만 항상 모든 디테일과 일치할 수는 없기 때문에 재구성이 완벽하지 않다. 그럼에도 불구하고 저자들은 본 논문의 결과가 접근 방식의 실행 가능성을 설득력 있게 보여주고 향후 개선을 위한 경로를 추적한다고 믿는다.

Method

1. Radiance fields and DreamFusion

Radiance fields

Radiance field (RF)는 3D 점 $x \in \mathbb{R}^3$를 불투명도 값 $\sigma(x) \in \mathbb{R}^{+}$과 색상 값 $c(x) \in \mathbb{R}^3$에 매핑하는 함수 쌍 $(\sigma(x), c(x))$이다. 이 두 함수가 신경망에 의해 구현될 때 RF를 neural radiance field (NeRF)라고 한다.

RF는 물체의 모양과 모양을 나타낸다. 이미지를 생성하기 위해 방출-흡수 모델을 사용하여 RF를 렌더링한다. $I \in \mathbb{R}^{3 \times H \times W}$가 이미지라고 가정하면 $I(u) \in \mathbb{R}^3$은 픽셀 $u$의 색상이다. $I(u)$를 계산하기 위해 카메라 중심에서 3D 이미지 평면의 점으로 해석되는 픽셀을 통해 광선 $r_u$를 투사한다. 이는 암시적으로 카메라 시점 $\pi \in SE(3)$을 설명한다. 그런 다음 일정한 간격 $\Delta$를 가지는 인덱스 \(\mathcal{N} = \{1, \ldots, N\}\)에 대하여 특정 개수의 샘플들 \((x_i \in r_u)_{i \in \mathcal{N}}\)을 얻는다. 색상은 다음과 같이 얻는다.

\[\begin{equation} I(u) = R (u; \sigma, c) = \sum_{i \in \mathcal{N}} (T_{i+1} - T_i) c (x_i) \\ T_i = \exp (- \Delta \sum_{j=0}^{i-1} \sigma (x_j)) \end{equation}\]

여기서 $T_i$는 광자가 재료에 흡수되지 않고 포인트 $x_i$에서 카메라 센서로 다시 전송될 확률이다.

중요한 것은 렌더링 함수 $R (u; \sigma, c)$가 미분 가능하여 표준 optimizer를 통해 모델을 학습육할 수 있다는 것이다. 구체적으로, RF는 $L^2$ 이미지 재구성 오차를 최소화하여 알려진 카메라 파라미터가 있는 이미지 $I$의 데이터셋 \(\mathcal{D} = \{(I, \pi)\}\)에 맞춰진다.

\[\begin{equation} \mathcal{L}_\textrm{rec} (\sigma, c; \mathcal{D}) = \frac{1}{\vert \mathcal{D} \vert} \sum_{(I, \pi) \in \mathcal{D}} \| I - R(\cdot; \sigma c, \pi) \|^2 \end{equation}\]

좋은 품질의 결과를 얻으려면 일반적으로 수십 또는 수백 개의 view 데이터셋이 필요하다.

여기서, 어떤 (알려지지 않은) 카메라 $\pi_0$에 해당하는 정확히 하나의 입력 이미지 $I_0$가 주어진 경우를 고려한다. 이 경우 단일 카메라에 대한 표준 시점 $\pi_0$을 가정할 수도 있다. 단일 교육 이미지로 위 식을 최적화하면 심각한 overfitting이 발생한다. loss가 0이지만 개체의 합리적인 3D 모델을 캡처하지 않는 쌍 $(\sigma, c)$를 찾는 것은 간단하다. 암시적으로 개체의 새로운 view를 상상하고 3D 재구성을 위해 누락된 정보를 제공하기 전에 사전 학습된 2D 이미지를 활용한다.

Diffusion models

Diffusion model은 이미지 $I$에 점진적으로 noise를 추가하는 프로세스를 반전하여 확률 분포 $p(I)$에서 샘플을 추출한다. Diffusion process는 분산 schedule \(\{\beta_t \in (0, 1)\}_{t=1}^T\)과 연관되며, 각 timestep에서 추가되는 noise의 양을 정의한다. 그러면 시간 $t$에서 샘플 $I$의 noisy한 버전은 다음과 같이 쓸 수 있다.

\[\begin{equation} I_t = \sqrt{\vphantom{1} \bar{\alpha}_t} I + \sqrt{1 - \bar{\alpha}_t} \epsilon \\ \epsilon \sim \mathcal{N}(0, I) \quad \alpha_t = 1 - \beta_t \quad \bar{\alpha}_t = \prod_{i=1}^t \alpha_i \end{equation}\]

그런 다음 noisy한 이미지 $I_t$과 noise 레벨 $t$를 입력으로 취하고 noise 성분 $\epsilon$을 예측하려고 시도하는 denoising 신경망 \(\hat{\epsilon} = \Phi (I_t; t)\)를 학습한다.

분포 $p(I)$에서 샘플을 추출하기 위해 샘플 $I_T \sim \mathcal{N} (0, I)$을 추출하는 것으로 시작한다. 그런 다음 지정된 샘플링 schedule에 따라 $\Phi$를 반복 적용하여 이미지의 noise를 점진적으로 제거하고 $p(I)$에서 샘플링된 $I_0$로 종료한다.

최신 diffusion model은 loss를 최소화하여 이미지의 대규모 컬렉션 \(\mathcal{D}' = \{I\}\)에서 학습된다.

\[\begin{equation} \mathcal{L}_\textrm{diff} (\Phi; \mathcal{D}') = \frac{1}{\vert \mathcal{D}' \vert} \sum_{I \in \mathcal{D}'} \| \Phi (\sqrt{\vphantom{1} \bar{\alpha}_t} I + \sqrt{1 - \bar{\alpha}_t} \epsilon, t) - \epsilon \|^2 \end{equation}\]

이 모델은 프롬프트 $e$로 컨디셔닝된 분포 $p(x \vert e)$에서 샘플을 추출하도록 쉽게 확장할 수 있다. 프롬프트에 대한 컨디셔닝은 네트워크 $\Phi$의 추가 입력으로 $e$를 추가하여 얻어지며 컨디셔닝 강도는 classifier-free guidance를 통해 제어할 수 있다.

DreamFusion and Score Distillation Sampling (SDS)

2D diffusion model $p(I \vert e)$와 프롬프트 $e$가 주어지면 DreamFusion은 여기에서 RF $(\sigma, c)$로 표시되는 해당 개념의 3D 변환을 추출한다. 카메라 파라미터 $\pi$를 랜덤으로 샘플링하고, 해당 view $I_\pi$를 렌더링하고, 모델 $p(I_\pi \vert e)$를 기반으로 view의 likelihood를 평가하고, 모델을 기반으로 생성된 view의 likelihood를 높이기 위하여 RF를 업데이트한다.

실제로 DreamFusion은 denoiser 네트워크를 고정된 critic으로 사용하고 gradient step을 취한다.

\[\begin{equation} \nabla_{(\sigma, c)} = \mathcal{L}_\textrm{SDS} (\sigma, c; \pi, e, t) = \mathbb{E}_{t, \epsilon} [w(t) (\Phi (\alpha_t I + \sigma_t \epsilon; t, e) - \epsilon) \cdot \nabla_{(\sigma, c)} I] \end{equation}\]

여기서 $I = R(\cdot; \sigma, c, \pi)$는 주어진 시점 $\pi$와 프롬프트 $e$에서 렌더링된 이미지이다. 이 프로세스를 Score Distillation Sampling (SDS)라고 한다.

위 식은 $\Phi$에 대한 Jacobian 항을 포함하지 않기 때문에 단순히 표준 diffusion model을 최적화하는 것과 다르다. 실제로 이 항을 제거하면 생성 품질이 향상되고 계산 및 메모리 요구 사항이 줄어든다.

좋은 3D 모양을 얻기 위해서는 DreamFusion에 이미지 샘플링에 사용하는 것보다 훨씬 큰 100의 매우 높은 안내 가중치로 classifier-free guidance를 사용하는 것이 필요하다. 결과적으로 생성은 다양성이 제한되는 경향이 있다. 주어진 프롬프트에 대해 가장 가능성이 높은 개체만 생성하므로 주어진 개체를 재구성하려는 본 논문의 목표와 양립할 수 없다.

2. RealFusion

본 논문의 목표는 단일 이미지 $I_0$에 포함된 객체의 3D 모델을 재구성하고 누락된 정보를 보충하기 위해 diffusion model $\Phi$에서 캡처된 prior를 활용하는 것이다. 두 가지 목적 함수를 동시에 사용하여 RF를 최적화하여 이를 달성한다.

1. 고정된 시점에서의 재구성 목적 함수
2. 각 iteration에서 랜덤하게 샘플링된 새로운 view에 대한 SDS 기반 prior 목적 함수

아래 그림은 전체 시스템의 다이어그램이다.

Single-image textual inversion as a substitute for alternative views

본 논문의 방법에서 가장 중요한 구성 요소는 대체 view 대신 단일 이미지 텍스트 inversion을 사용한다는 것이다. 이상적으로, 재구성 프로세스를 $I_0$에 있는 개체의 multi-view 이미지, 즉 $p(I \vert I_0)$의 샘플로 컨디셔닝하고 싶다. 이러한 이미지를 사용할 수 없기 때문에 대신 이 multi-view 정보에 대한 대안으로 이미지 $I_0$에 대해 특별히 텍스트 프롬프트 $e^{(I_0)}$를 합성한다.

본 논문의 아이디어는 $p(I \vert I_0)$의 유용한 근사치를 제공하기 위해 프롬프트 $e^{(I_0)}$를 엔지니어링하는 것이다. Pseudo-alternative-view 역할을 하는 입력 이미지의 랜덤 augmentation $g(I_0), g \in G$를 생성하여 이를 수행한다. 이러한 augmentation을 미니 데이터셋 \(\mathcal{D}' = \{g(I_0)\}_{g \in G}\)로 사용하고 프롬프트 $e^{(I_0)}$에 대한 diffusion loss \(\mathcal{L}_\textrm{diff} (\Phi(\cdot; e^{(I_0)}))\)를 최적화한다. 이 때 다른 모든 텍스트 임베딩과 모델 파라미터를 고정한다.

실제로 프롬프트는 “$\langle e \rangle$의 이미지”와 같은 템플릿에서 자동으로 파생된다. 여기서 “$\langle e \rangle$” ($= e^{(I_0)}$)는 diffusion model의 텍스트 인코더 vocabulary에 도입된 새로운 토큰이다. 최적화 절차는 최근에 제안된 textual-inversion 방법을 반영하고 일반화한다. Textual-inversion과 달리 단일 이미지 설정에서 작업하고 mutli-view가 아닌 학습을 위해 이미지 augmentation을 활용한다.

위 그림은 임베딩 $\langle e \rangle$에서 캡처된 디테일의 양을 보여준다.

Coarse-to-fine training

본 논문의 coarse-to-fine 학습 방법론을 설명하기 위해 먼저 기본 RF 모델인 InstantNGP를 간략하게 소개해야 한다. InstantNGP는 여러 해상도에서 feature grd 집합 \(\{G_i\}_{i=1}^L\)의 vertex에 feature를 저장하는 grid 기반 모델이다. 이러한 grid의 해상도는 가장 coarse한 해상도와 가장 fine한 해상도 사이의 기하학적 진행으로 선택되며 feature grid는 동시에 학습된다.

저자들은 계산 효율성과 학습 속도로 인해 기존의 MLP 기반 NeRF보다 InstantNGP를 선택하였다. 그러나 최적화 절차는 때때로 개체 표면에 작은 불규칙성을 생성한다. Coarse-to-fine 방식으로 학습하면 이러한 문제를 완화하는 데 도움이 된다. 학습의 전반부에서는 저해상도 feature grid \(\{G_i\}_{i=1}^{L/2}\)만 최적화하고 후반부에서는 모든 feature grid \(\{G_i\}_{i=1}^L\)를 최적화한다. 이 전략을 사용하여 효율적인 학습과 고품질 결과의 이점을 모두 얻는다.

Normal vector regularization

다음으로 형상이 매끄러운 법선을 갖도록 장려하기 위해 새로운 정규화 항을 도입한다. 이 항의 도입은 RF 모델이 때때로 낮은 수준의 아티팩트가 있는 표면을 생성한다는 관찰에 의한 것이다. 이러한 아티팩트를 해결하기 위해 RF가 매끄럽게 변하는 법선 벡터를 갖도록 권장한다. 특히, 3D가 아닌 2D에서 이 정규화를 수행한다.

각 iteration에서 RGB와 불투명도 값을 계산하는 것 외에도 광선을 따라 각 지점에 대한 법선을 계산하고 raymarching 방정식을 통해 이를 집계하여 법선 $N \in \mathbb{R}^{H \times W \times 3}$을 얻는다. Loss는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{normal} = \| N - \textrm{stopgrad} (\textrm{blur} (N, k)) \|^2 \end{equation}\]

여기서 $\textrm{stopgrad}$는 stop-gradient 연산이고 $\textrm{blur}(\cdot, k)$는 커널 크기가 $k$인 Gaussian blur이다 ($k = 9$ 사용).

3D에서 법선을 정규화하는 것이 더 일반적일 수 있지만 2D에서 작업하면 정규화 항의 분산이 줄어들고 우수한 결과를 얻을 수 있다.

Mask loss

입력 이미지 외에도 모델은 재구성하려는 개체의 마스크도 활용합한다. 실제로 기존의 이미지 매팅 모델을 사용하여 모든 이미지에 대해 이 마스크를 얻는다.

고정된 레퍼런스 시점 $R (\sigma, \pi_0) \in \mathbb{R}^{H \times W}$과 개체 마스크 $M$에서 렌더링된 불투명도 간의 차이에 간단한 $L^2$ loss 항을 추가하여 간단한 방식으로 이 마스크를 통합한다.

\[\begin{equation} \mathcal{L}_\textrm{rec, mask} = \| O - M \|^2 \end{equation}\]

최종 목적 함수는 다음 네 가지 항으로 구성된다.

\[\begin{aligned} \nabla_{\sigma, c} \mathcal{L} = \;& \nabla \mathcal{L}_\textrm{SDS} + \lambda_\textrm{normals} \cdot \nabla \mathcal{L}_\textrm{normals} \\ &+ \lambda_\textrm{image} \cdot \nabla \mathcal{L}_\textrm{image} + \lambda_\textrm{mask} \cdot \nabla \mathcal{L}_\textrm{mask} \end{aligned}\]

위 식의 상단 라인은 prior 목적 함수에 해당하고 하단 라인은 재구성 목적 함수에 해당한다.

Experiments

• 데이터셋: OpenImages
• 구현 디테일
  • Diffusion model prior: LAION에서 학습된 Stable Diffusion
  • InstantNGP: 해상도 레벨 16개, feature 차원 = 2, 최대 해상도 2048
  • 카메라: 평면 위 반경 1.8의 구에서 15도 각도에서 원점을 바라보도록 배치됨
  • \(\lambda_\textrm{image}\) = 5.0, \(\lambda_\textrm{mask}\) = 0.5, \(\lambda_\textrm{normals}\) = 0.5

1. Quantitative results

다음은 CO3D 데이터셋에서 Shelf-Supervised와 정성적으로 비교한 것이다.

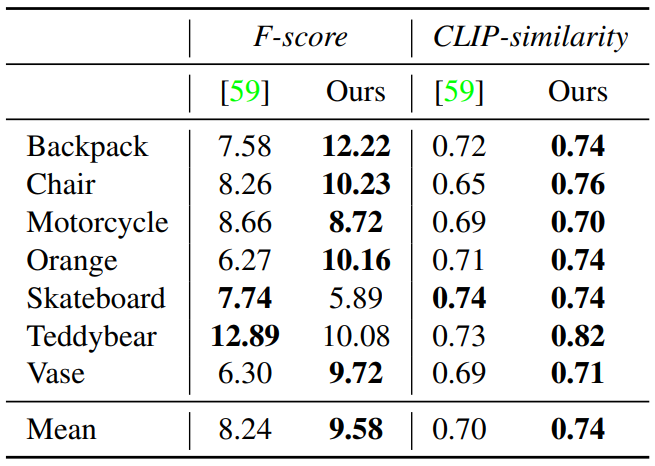
다음은 Shelf-Supervised와 7가지 카테고리에서 정량적으로 비교한 표이다.

2. Qualitative results

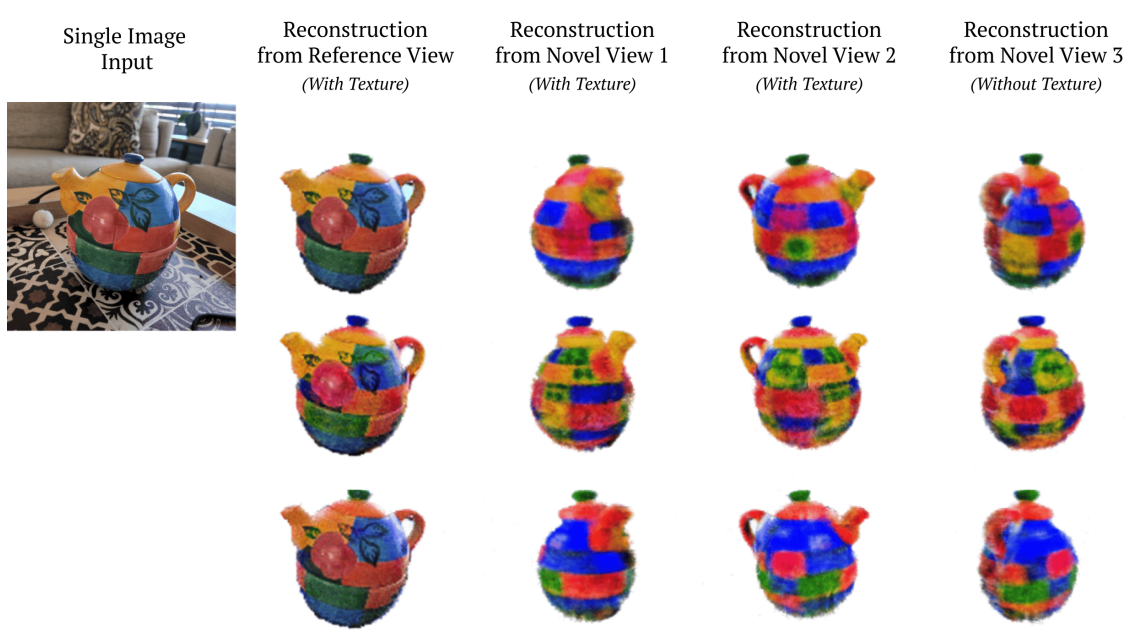
다음은 RealFusion의 정성적 결과이다.

다음은 multi-modal 이미지 재구성 예시이다.

다음은 RealFusion의 2가지 일반적인 실패 모드이다.

어떤 경우에는 모델이 수렴하지 못하고 어떤 경우에는 의미상 올바르지 않더라도 전면 view를 개체의 후면에 복사한다.

3. Analysis and Ablations

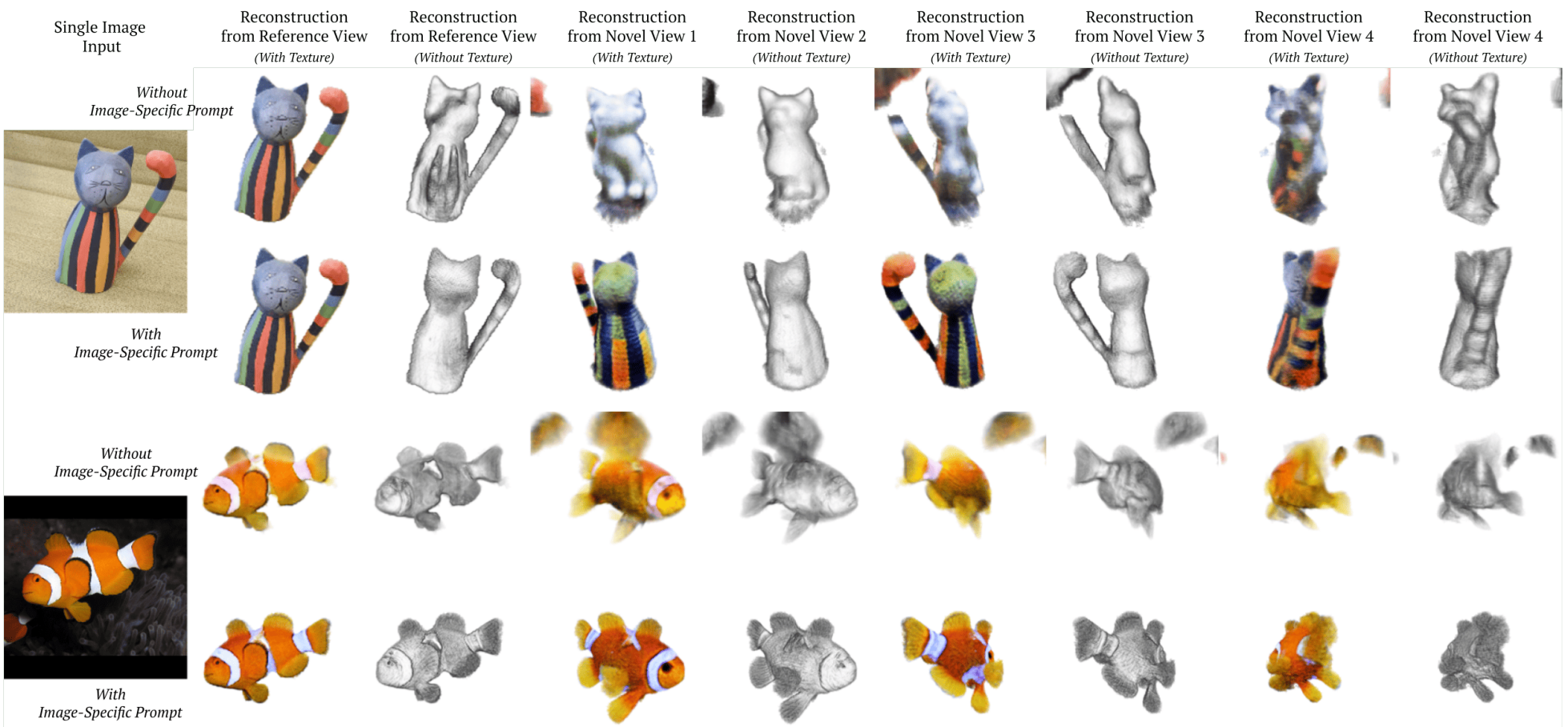
다음은 재구성 품질 측면에서 단일 이미지 textual inversion의 효과를 시각화한 것이다.

다음은 coarse-to-fine 학습의 효과를 시각화한 것이다.

다음은 재구성 품질 측면에서 부드러운 법선의 효과를 시각화한 것이다.

다음은 Stable Diffusion과 CLIP prior를 비교한 결과이다.