[논문리뷰] Real-time Photorealistic Dynamic Scene Representation and Rendering with 4D Gaussian Splatting
ICLR 2024. [Paper] [Page] [Github]
Zeyu Yang, Hongye Yang, Zijie Pan, Xiatian Zhu, Li Zhang
Fudan University | University of Surrey
16 Oct 2023
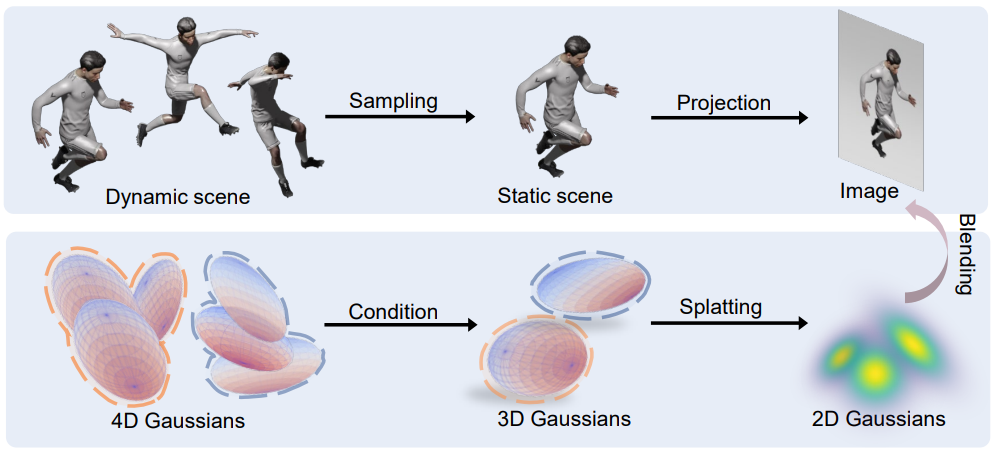
Introduction
2D 이미지에서 동적 장면을 모델링하고 사실적인 새로운 뷰를 실시간으로 렌더링하는 것은 컴퓨터 비전 및 그래픽에서 매우 중요하다. NeRF와 같은 최근의 혁신을 통해 사실적인 정적 장면 렌더링이 가능해졌지만 이러한 기술을 동적 장면에 적용하는 것은 여러 요인으로 인해 어렵다. 물체의 움직임은 재구성을 복잡하게 만들고 시간적 장면 역학은 상당한 복잡성을 추가한다. 더욱이 실제 애플리케이션은 동적 장면을 단안 동영상(monocular video)으로 캡처하는 경우가 많기 때문에 각 프레임에 대해 별도의 정적 장면 표현을 학습한 다음 이를 동적 장면 모델로 결합하는 것이 비현실적이다. 핵심 과제는 본질적인 상관관계를 유지하고 서로 다른 timestep에 걸쳐 관련 정보를 공유하는 동시에 관련되지 않은 시공간 위치 간의 간섭을 최소화하는 것이다.
동적인 novel view synthesis 방법은 두 가지 그룹으로 분류할 수 있다. 첫 번째 그룹은 장면 모션을 명시적으로 모델링하지 않고도 6D plenoptic function을 학습하기 위해 low-rank decomposition을 포함한 MLP 또는 그리드와 같은 구조를 사용한다. 서로 다른 시공간적 위치에 걸쳐 상관관계를 포착하는 이러한 방법의 효율성은 선택한 데이터 구조의 고유한 특성에 따라 달라진다. 그러나 기본 장면 모션에 적응하는 유연성이 부족하다. 결과적으로 이러한 방법은 시공간적 위치에 걸쳐 파라미터를 공유하는 문제로 인해 잠재적인 간섭이 발생하거나 너무 독립적으로 작동하여 물체의 움직임으로 인한 고유 상관관계를 활용하는 데 어려움을 겪는다.
대조적으로, 또 다른 그룹은 장면 역학이 일관된 기본 표현의 움직임이나 변형에 의해 유도된다고 제안한다. 이러한 방법은 장면 모션을 명시적으로 학습하여 공간과 시간에 걸쳐 상관 관계를 더 잘 활용할 수 있는 가능성을 제공한다. 그럼에도 불구하고 첫 번째 방법 그룹에 비해 복잡한 실제 장면에서 유연성과 확장성이 감소한다.
이러한 한계를 극복하기 위해 본 논문에서는 4D Gaussian 세트로 장면의 기본 시공간 4D 볼륨을 근사화하여 task를 재구성하였다. 특히, 4D rotation을 통해 Gaussian은 4D manifold에 맞추고 장면 고유 동작을 캡처할 수 있다. 또한 동적 장면에서 나타나는 외형의 시간적 진화를 모델링하기 위해 동적 장면에 대한 Spherical Harmonics를 일반화한 Spherindrical Harmonics를 도입하였다. 이 접근 방식은 다양한 조명 조건을 갖춘 복잡하고 동적인 장면에서 고해상도의 사실적인 새로운 뷰의 end-to-end 학습과 실시간 렌더링을 지원하는 최초의 모델이다. 또한 제안된 표현은 공간적, 시간적 차원 모두에서 해석 가능하고 확장성이 뛰어나며 적응성이 뛰어나다.
Method

1. Preliminary: 3D Gaussian Splatting
3D Gaussian Splatting은 이방성 Gaussian을 사용하여 정적 3D 장면을 표현한다. 잘 커스터마이징된 GPU 친화적인 rasterizer를 통해 이 표현을 통해 충실도가 높은 새로운 뷰를 실시간으로 합성할 수 있다.
Representation of 3D Gaussians
3D Gaussian Splatting에서는 장면이 3D Gaussian cloud로 표현된다. 각 Gaussian는 이론적으로 무한한 범위와 정규화되지 않은 Gaussian 함수로 정의된 주어진 공간적 위치 $x \in \mathbb{R}^3$에 대한 영향을 갖는다.
\[\begin{equation} p(x \vert \mu, \Sigma) = \exp \bigg( -\frac{1}{2} (x-\mu)^\top \Sigma^{-1} (x-\mu) \bigg) \end{equation}\]여기서 $\mu \in \mathbb{R}^3$은 평균 벡터이고 $\Sigma \in \mathbb{R}^{}$은 공분산 행렬이다. 다변량(multivariate) Gaussian의 정규화되지 않은 Gaussian 함수는 해당 조건 분포와 주변 확률 분포(marginal distribution)의 정규화되지 않은 Gaussian 함수의 곱으로 인수분해될 수 있다.
3D Gaussian의 평균 벡터 $\mu$는 $μ = (\mu_x, \mu_y, \mu_z)$로 parameterize되고, 공분산 행렬 $\Sigma$는 scaling matrix $S$와 rotation matrix $R$를 사용하여 $\Sigma = RSS^\top R^\top$로 인수분해된다. 여기서 $S = \textrm{diag}(s_x, s_y, s_z)$는 대각 성분으로 요약되는 반면 $R$은 단위 quaternion $q$로 구성된다. 또한 3D Gaussian에는 불투명도 $\alpha$와 함께 뷰에 따른 색상을 표현하기 위한 Spherical Harmonics(SH) 계수 집합도 포함되어 있다.
위의 모든 파라미터는 렌더링 loss의 supervision 하에 최적화될 수 있다. 최적화 프로세스 중에 3D Gaussian Splatting은 Gaussian 컬렉션에 대해 주기적으로 densification과 pruning을 수행하여 형상 및 렌더링 품질을 더욱 향상시킨다.
Differentiable rasterization via Gaussian splatting
렌더링 시 extrinsic matrix가 $E$이고 intrinsic matrix가 $K$인 뷰 $\mathcal{I}$의 픽셀 $(u, v)$가 주어지면 해당 색상 $\mathcal{I}(u, v)$는 깊이에 따라 정렬된 보이는 3D Gaussian을 혼합하여 계산될 수 있다.
\[\begin{equation} \mathcal{I} (u,v) = \sum_{i=1}^N p_i (u, v; \mu_i^\textrm{2d}, \Sigma_i^\textrm{2d}) \alpha_i c_i (d_i) \prod_{j=1}^{i-1} (1 - p_j (u, v; \mu_j^\textrm{2d}, \Sigma_j^\textrm{2d}) \alpha_j) \end{equation}\]여기서 $c_i$는 보는 방향 $d_i$에서 $i$번째로 보이는 Gaussian의 색상을 나타내고, $\alpha_i$는 불투명도를 나타내며, $p_i (u, v)$는 픽셀 $(u, v)$에서 $i$번째 Gaussian의 확률 밀도이다.
이미지 공간에서 $p_i (u, v)$를 계산하기 위해 perspective transformation을 선형화한다. 그런 다음 투영된 3D Gaussian을 2D Gaussian으로 근사화할 수 있다. 2D Gaussian의 평균은 다음과 같이 얻는다.
\[\begin{equation} \mu_i^\textrm{2d} = \textrm{Proj} (\mu_i \vert E, K)_{1:2} \end{equation}\]여기서 $\textrm{Proj} (\cdot \vert E, K)$는 intrinsic $K$와 extrinsic $E$가 주어진 경우 world space에서 image space으로의 변환을 나타낸다. 공분산 행렬은 다음과 같다.
\[\begin{equation} \Sigma_i^\textrm{2d} = (JE \Sigma E^\top J^\top)_{1:2, 1:2} \end{equation}\]여기서 $J$는 perspective transformation의 Jacobian 행렬이다.
2. 4D Gaussian for Dynamic Scenes
Problem formulation and 4D Gaussian splatting
동적 장면 모델링을 위해 3D Gaussian Splatting의 공식을 확장하려면 재구성이 필요하다. 동적 장면에서 뷰 $\mathcal{I}$에 대한 픽셀은 더 이상 이미지 평면의 한 쌍의 공간 좌표 $(u, v)$로만 인덱싱될 수 없으며, 추가 타임스탬프 $t$가 개입한다. 이는 식을 다음과 같이 확장하여 공식화된다.
\[\begin{equation} \mathcal{I} (u,v,t) = \sum_{i=1}^N p_i (u, v, t) \alpha_i c_i (d) \prod_{j=1}^{i-1} (1 - p_j (u, v, t) \alpha_j) \end{equation}\]$p_i (u, v, t)$는 조건부 확률 $p_i (u, v \vert t)$와 시간 $t$에서의 주변 확률 분포 $p_i (t)$의 곱으로 추가 인수분해될 수 있다.
\[\begin{equation} \mathcal{I} (u,v,t) = \sum_{i=1}^N p_i (t) p_i (u, v \vert t) \alpha_i c_i (d) \prod_{j=1}^{i-1} (1 - p_j (t) p_j (u, v \vert t) \alpha_j) \end{equation}\]$p_i (x, y, z, t)$를 4D Gaussian으로 설정한다. 조건부 분포 $p(x, y, z \vert t)$도 3D Gaussian이므로 유사하게 $p(u, v \vert t)$를 평면 Gaussian으로 유도할 수 있다.
이어서 4D Gaussian을 어떻게 표현하느냐 하는 문제가 나온다. 자연스러운 해결책은 공간과 시간에 대해 별개의 관점을 채택하는 것이다. 즉, $(x, y, z)$와 $t$가 서로 독립적이라고 생각하는 것이다.
\[\begin{equation} p_i (x, y, z \vert t) = p_i (x , y, z) \end{equation}\]이 가정 하에서 $\mathcal{I} (u,v,t)$에 대한 식은 원래 3D Gaussian에 추가 1D Gaussian $p_i (t)$를 추가하여 구현할 수 있다. 이 디자인은 3D Gaussian에 시간적 확장을 부여하거나 렌더링 timestep이 $p_i (t)$의 기대값에서 벗어날 때 불투명도를 낮추는 것으로 볼 수 있다. 그러나 이 접근 방식은 4D manifold의 합리적인 피팅을 달성할 수 있지만 장면의 기본 모션을 포착하기 어렵다.
Representation of 4D Gaussian
이 문제를 해결하기 위해 일관된 통합 4D Gaussian 모델을 공식화하여 시간과 공간 차원을 동일하게 처리하는 것이 좋다. 3D Gaussian Splatting과 유사하게 모델 최적화를 용이하게 하기 위해 공분산 행렬 $\Sigma$를 4D 타원체의 구성으로 parameterize한다.
\[\begin{equation} \Sigma = R S S^\top R^\top \end{equation}\]여기서 $S$는 scaling matrix이고 $R$은 4D rotation matrix이다. $S$는 대각 행렬이므로 $S = \textrm{diag}(s_x, s_y, s_z, s_t)$와 같이 대각 성분으로 나타낼 수 있다. 반면, 4D 유클리드 공간의 회전은 한 쌍의 isotropic rotation으로 분해될 수 있으며, 각 회전은 quaternion으로 표시될 수 있다.
구체적으로, 각각 왼쪽 isotropic rotation $q_l = (a, b, c, d)$와 오른쪽 isotropic rotation $q_r = (p, q, r, s)$가 주어지면 $R$은 다음과 같이 구성할 수 있다.
\[\begin{equation} R = L(q_l) R(q_r) = \begin{bmatrix} a & -b & -c & -d \\ b & a & -d & c \\ c & d & a & -b \\ d & -c & b & a \end{bmatrix} \begin{bmatrix} p & -q & -r & -s \\ q & p & s & -r \\ r & -s & p & q \\ s & r & -q & p \end{bmatrix} \end{equation}\]4D Gaussian의 평균은 $\mu = (\mu_x, \mu_y, \mu_z, \mu_t)$와 같은 4개의 스칼라로 표시될 수 있다.
결과적으로 조건부 3D Gaussian은 다음 식을 사용하여 다변량 Gaussian의 속성에서 파생될 수 있다.
\[\begin{aligned} \mu_{xyz \vert t} &= \mu_{1:3} + \Sigma_{1:3,4} \Sigma_{4,4}^{-1} (t - \mu_t) \\ \Sigma_{xyz \vert t} &= \Sigma_{1:3,1:3} - \Sigma_{1:3,4} \Sigma_{4,4}^{-1} \Sigma_{4,1:3} \end{aligned}\]$p_i (x, y, z \vert t)$는 3D Gaussian이므로 $p_i (u, v \vert t)$는 3D Gaussian Splatting과 같은 방법으로 유도할 수 있다. 또한 주변 확률 분포 $p_i (t)$는 1D Gaussian이다.
\[\begin{equation} p(t) = \mathcal{N}(t; \mu_4, \Sigma_{4,4}) \end{equation}\]색상과 불투명도를 누적할 때 $p_i (t)$를 고려하여 3D Gaussian Splatting에서 제안된 매우 효율적인 타일 기반 rasterizer를 적용하여 이 프로세스를 근사화할 수 있다.
4D spherindrical harmonics
원래 3D Gaussian Splatting에서 뷰에 따른 색상 $c_i (d)$는 일련의 SH 계수로 표시된다. 현실 세계의 동적인 장면을 보다 충실하게 모델링하려면 다양한 시점에 따른 외형 변화와 시간이 지남에 따라 색상이 변할 수 있도록 해야 한다.
프레임워크의 유연성을 활용하는 간단한 솔루션은 서로 다른 Gaussian을 직접 사용하여 서로 다른 시간에 동일한 지점을 나타내는 것이다. 그러나 이 접근 방식은 동일한 객체의 중복 및 중복 표현으로 이어져 최적화가 어렵다. 대신 저자들은 각 Gaussian의 출현 시간 변화를 직접적으로 나타내는 spherical harmonics(SH)의 4D 확장을 활용하기로 선택했다. 그러면 색상은 $c_i (d, t)$로 조작될 수 있다. 여기서 $d = (\theta, \phi)$는 구면 좌표계에서 정규화된 뷰 방향이고 $t$는 주어진 Gaussian의 기대값과 시점 간의 시간 차이이다.
본 논문은 SH를 다양한 1D 기반 함수와 병합하여 구성된 일련의 4D spherindrical harmonics(4DSH)의 조합으로 $c_i (d, t)$를 나타낼 것을 제안하였다. 계산상의 편의를 위해 채택된 1D 기반 함수로 푸리에 급수(Fourier series)를 사용한다. 결과적으로 4DSH는 다음과 같이 표현될 수 있다.
\[\begin{equation} Z_{nl}^m (t, \theta, \phi) = \cos \bigg( \frac{2\pi n}{T} t \bigg) Y_l^m (\theta, \phi) \end{equation}\]여기서 $Y_l^m$은 3D SH이다. $l \ge 0$은 degree를 나타내며, $m$은 $−l \le m \le l$을 만족하는 order이다. $n$은 푸리에 급수(Fourier series)의 차수이다. 4DSH는 spherindrical 좌표계에서 orthonormal basis를 형성한다.
3. Training
3D Gaussian Splatting을 따라 학습 중에 중간 최적화와 밀도 제어를 수행한다. 본 논문의 최적화 프로세스는 완전히 end-to-end이며, 기존의 프레임별 또는 다단계 학습 접근 방식과 달리 언제든지 샘플링하고 볼 수 있는 기능을 통해 전체 동영상을 처리할 수 있다.
Optimization
최적화에서는 렌더링 loss만 supervision으로 사용한다. 대부분의 장면에서 3D Gaussian Splatting의 기본 학습 일정과 결합하는 것은 만족스러운 결과를 얻기에 충분하다. 그러나 보다 극적인 변화가 있는 일부 장면에서는 시간적 깜박임 및 jitter와 같은 문제가 관찰된다. 저자들은 이것이 샘플링 기술로 인해 발생할 수 있다고 생각하였다. 저자들은 prior 정규화를 채택하는 대신 시간에 따른 간단한 batch 샘플링이 더 우수하여 동적 시각적 콘텐츠가 더 원활하고 시각적으로 보기 좋게 표시된다는 사실을 발견했다.
Densification in spacetime
밀도 제어 측면에서 단순히 view space 위치 기울기의 평균 크기를 고려하는 것만으로는 시간이 지남에 따라 재구성이 부족한지와 재구성이 과다한지 평가하기에는 충분하지 않다. 이 문제를 해결하기 위해 저자들은 추가 밀도 제어 지표로 $\mu_t$의 평균 기울기를 통합하였다. 또한 과도하게 재구성되기 쉬운 영역에서는 Gaussian 분할 중에 공간적 위치와 시간적 위치의 공동 샘플링을 사용하였다.
Experiments
- 데이터셋: Plenoptic Video, D-NeRF
- 구현 디테일
- iteration: 30,000
- batch size: 8
- 학습 중간에 densification을 중단
- loss 가중치, learning rate, threshold 등 hyperparameter는 3D Gaussian Splatting을 따름
- 학습 초기에 $q_l$과 $q_r$을 단위 quaternion으로 초기화
- 초기 시간 scaling을 장면 길이의 절반을 설정
- 시간 $t$에서 뷰를 렌더링할 때 $p(t) < 0.05$인 Gaussian 필터를 적용
- Plenoptic Video 데이터셋의 경우 colmap이 재구성하지 못한 먼 배경에 맞게 전체 장면을 둘러싸는 구에 균일하게 분포된 100,000개의 추가 포인트로 Gaussian을 추가로 초기화하고 10,000 iteration 후 최적화를 종료
1. Results of Dynamic Novel View Synthesis
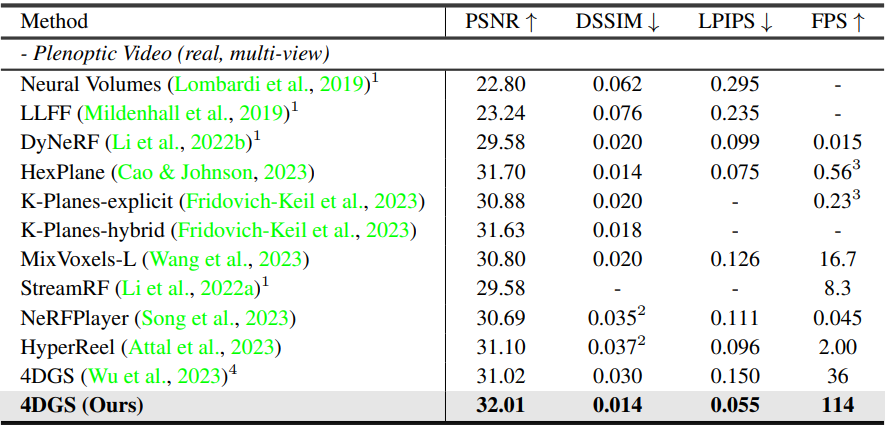
다음은 Plenoptic Video 벤치마크에서 SOTA 방법들과 비교한 결과이다.

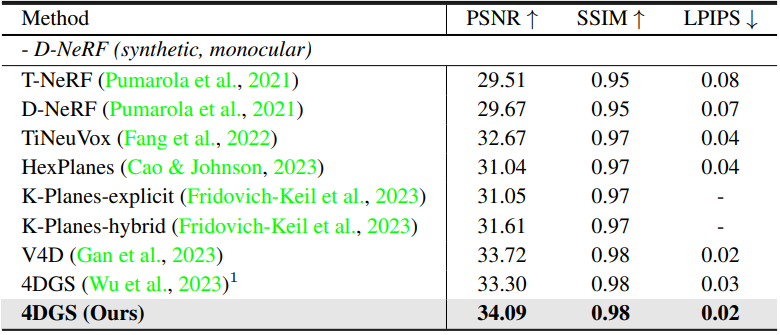
다음은 D-NeRF 데이터셋의 monocular dynamic scene에 대한 정량적 비교 결과이다.
2. Ablation and Analysis
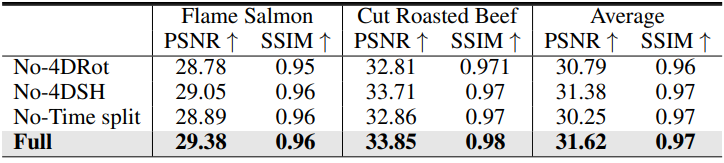
다음은 ablation study 결과이다.
다음은 4D Gaussian의 역학을 시각화한 것이다. GT Flow는 VideoFlow로 추출되었다.
