[논문리뷰] Residual Denoising Diffusion Models (RDDM)
CVPR 2024. [Paper] [Github]
Jiawei Liu, Qiang Wang, Huijie Fan, Yinong Wang, Yandong Tang, Liangqiong Qu
Chinese Academy of Sciences | Shenyang University | South China University of Technology | The University of Hong Kong
25 Aug 2023
Introduction
CNN 기반의 이미지 복원 방법은 다양한 이미지 degradation 프로세스를 효과적으로 모델링하고 degrade된 입력 이미지에서 선명한 이미지를 복구할 수 있다. 생성적 적대 학습을 통해 CNN은 이미지를 합성하고 편집할 수 있다. 그러나 CNN과 GAN을 사용하여 다양한 task를 처리하려면 별도의 네트워크 구조, loss function, 학습 전략을 생성해야 한다. 반면, diffusion model은 UNet 네트워크 구조만을 사용한 noise-to-image 매핑, $\ell_1$ loss, 간단한 denoising 학습 프로세스를 통해 다양하고 사실적인 이미지를 생성할 수 있다. 최근 조건부 diffusion model은 이미지 편집, 이미지 인페인팅, 이미지 복원 등 다양한 task에서 인기를 얻고 있다. 이러한 방법들은 원본 denoising diffusion process를 수정하지 않고 복원 프로세스를 가이드하기 위한 조건 입력으로 degrade된 이미지를 사용하여 diffusion model을 이미지 복원 task로 확장한다. 그러나 noise로부터 시작되는 reverse process는 불필요한 것으로 보이며, degrade된 이미지가 이미 알려져 있기 때문에 이미지 복원 task에 부당한 복잡성을 초래한다.
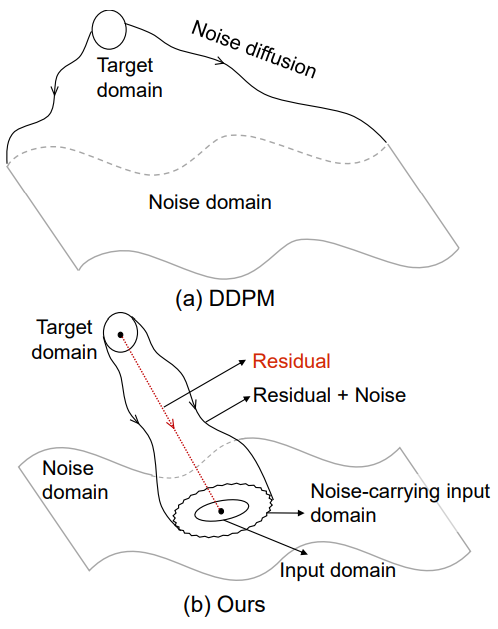
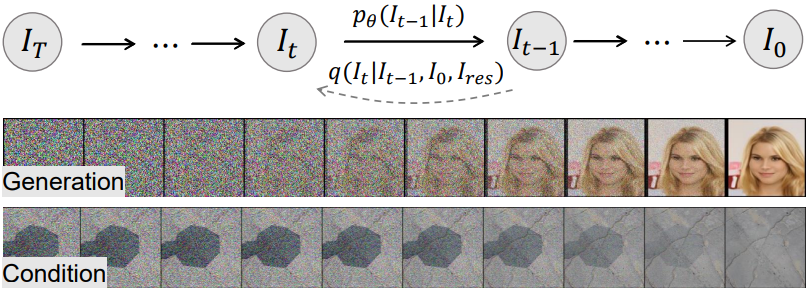
본 논문에서는 이미지 생성과 복원 모두를 위한 새롭고 통합적이며 해석 가능한 프레임워크인 Residual Denoising Diffusion Model (RDDM)을 제안한다. RDDM에서 residual은 타겟 영역에서 입력 영역으로의 directional diffusion을 나타내고, noise는 diffusion process의 랜덤 perturbation을 나타낸다. 위 그림에서 볼 수 있듯이 RDDM은 타겟 도메인을 noise가 있는 입력 도메인으로 확산시키는 반면, DDPM은 타겟 도메인을 noise 도메인으로 확산시킨다. 이미지 복원의 경우 RDDM은 forward diffusion 방향을 명확하게 표시하고 residual을 통해 생성 프로세스를 명시적으로 가이드할 수 있는 반면, DDPM은 diffusion process의 입력 도메인에 대한 정보를 포함하지 않고 조건부 입력을 통해 생성 프로세스를 암시적으로 가이드한다.
구체적으로, 본 논문은 입력 없는 이미지 생성과 조건부 입력을 사용한 이미지 복원을 모두 지원하기 위해 residual과 noise의 동시 diffusion을 허용하는 새로운 forward process를 재정의했다. 하나의 계수 schedule을 사용하여 noise와 이미지의 혼합 비율을 제어하는 이전 diffusion model과 달리, RDDM은 residual과 noise의 diffusion 속도를 제어하기 위해 두 개의 독립적인 계수 schedule을 사용한다. 저자들은 이러한 독립적인 diffusion 특성이 reverse process에서도 분명하다는 것을 발견했다. 예를 들어 테스트 중에 특정 범위 내에서 계수 schedule을 재조정해도 이미지 생성 결과에 영향을 미치지 않으며 먼저 residual을 제거한 다음 denoising을 수행하여 의미론적으로 일관된 이미지를 생성할 수도 있다. RDDM은 널리 사용되는 diffusion model과 호환된다. 즉, 샘플링 프로세스는 계수 schedule을 변환하여 DDPM 및 DDIM의 프로세스와 일치한다. 또한 RDDM은 기본적으로 조건부 입력을 지원하므로 $\ell_1$ 손실만으로 학습된 네트워크가 SOTA 이미지 복원 방법과 경쟁할 수 있다. 저자들은 RDDM이 diffusion model에 대한 residual의 중요성을 강조하면서 통합된 image-to-image translation 방법론을 촉진할 수 있을 것으로 예상한다.
Residual Denoising Diffusion Models
1. Directional Residual Diffusion Process with Perturbation
본 논문은 새로운 forward diffusion process를 제안한다.
\[\begin{equation} I_t = I_{t-1} + I_t^\textrm{res}, \quad I_t^\textrm{res} \sim \mathcal{N} (\alpha_t I_\textrm{res}, \beta_t^2 I) \end{equation}\]여기서 $I_t^\textrm{res}$는 state $I_{t-1}$에서 state $I_t$까지 랜덤 noise perturbation이 있는 directional residual diffusion을 나타낸다. 입력 도메인 $I_\textrm{in}$과 타겟 도메인 $I_0$ 사이의 차이는 residual $I_\textrm{res}$로 표시된다. 즉, $I_\textrm{res} = I_\textrm{in} − I_0$이다. 두 hyperparameter의 집합 $\alpha_t$와 $\beta_t$는 각각 residual과 noise diffusion을 제어한다. $I_t$는 reparameterization을 통해 얻을 수 있다.
\[\begin{aligned} I_t &= I_{t-1} + \alpha_t I_\textrm{res} + \beta_t \epsilon_{t-1} \\ &= I_{t-2} + (\alpha_{t-1} + \alpha_t) I_\textrm{res} + (\sqrt{\beta_{t-1}^2 + \beta_t^2}) \epsilon_{t-2} \\ &= \ldots \\ &= I_0 + \bar{\alpha}_t I_\textrm{res} + \bar{\beta}_t \epsilon \end{aligned}\] \[\begin{equation} \epsilon_{t-1}, \epsilon_{t-2}, \ldots, \epsilon \sim \mathcal{N} (0, I) \\ \bar{\alpha}_t = \sum_{i=1}^t \alpha_i, \quad \bar{\beta}_t = \sqrt{\sum_{i=1}^t \beta_i^2}, \quad t = 1, 2, \ldots, T \end{equation}\]$t = T$이면 \(\bar{\alpha}_T = 1\)이고
\[\begin{equation} I_T = I_0 = \bar{\alpha}_T I_\textrm{res} + \bar{\beta}_T \epsilon = I_\textrm{in} + \bar{\beta}_T \epsilon \end{equation}\]이다. 이미지 생성의 경우 \(I_\textrm{in} = 0, \bar{\beta}_T = 1, I_T = \epsilon\)이다. 이미지 복원의 경우 \(\bar{\beta}_T > 0\)이고 \(I_T = I_\textrm{in} + \bar{\beta}_T \epsilon\)이다. 여기서 이미지 생성을 위한 $I_T$는 순수한 Gaussian noise를 나타내고, 이미지 복원을 위한 $I_T$는 noise 포함하는 입력을 설명한다. Forward process의 결합 확률 분포는 다음과 같이 정의될 수 있다.
\[\begin{equation} q(I_{1:T} \vert I_0, I_\textrm{res}) := \prod_{t=1}^T q(I_t \vert I_{t-1}, I_\textrm{res}) \\ q(I_t \vert I_{t-1}, I_\textrm{res}) := \mathcal{N} (I_t; I_{t-1} + \alpha_t I_\textrm{res}, \beta_t^2 I) \end{equation}\]주변 확률 분포는 다음과 같다.
\[\begin{equation} q (I_t \vert I_0, I_\textrm{res}) = \mathcal{N} (I_t; I_0 + \bar{\alpha}_t I_\textrm{res}, \bar{\beta}_t^2 I) \end{equation}\]2. Perturbed Generation Process and Deterministic Implicit Sampling
확률론적 생성 프로세스와 결정론적 생성 프로세스를 통합하기 위해 $I_0$와 $I_\textrm{res}$가 주어지면 $I_t$에서 $I_{t−1}$로의 전송 확률을 정의한다.
\[\begin{equation} q_\sigma (I_{t-1} \vert I_t, I_0, I_\textrm{res}) := \mathcal{N} (I_{t-1}; I_0 + \bar{\alpha}_{t-1} I_\textrm{res} + \sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2} \frac{I_t - (I_0 + \bar{\alpha}_t I_\textrm{res})}{\bar{\beta}_t}, \sigma_t^2 I) \\ \textrm{where} \quad \sigma_t^2 = \frac{\eta \beta_t^2 \bar{\beta}_{t-1}^2}{\bar{\beta}_t^2} \end{equation}\]$\eta$는 생성 프로세스가 랜덤인지 ($\eta = 1$) 결정론적인지 ($\eta = 0$)를 제어하는 hyperparameter이다. 위 식에 의해 생성 프로세스는 다음과 같이 정의된다.
\[\begin{equation} p_\theta (I_{t-1} \vert I_t) = q_\sigma (I_{t-1} \vert I_t, I_0^\theta, I_\textrm{res}^\theta) \\ \textrm{where} \quad I_0^\theta = I_t - \bar{\alpha}_t I_\textrm{res}^\theta - \bar{\beta}_t \epsilon_\theta \end{equation}\]위 식을 사용하여 $x_{t−1}$은 다음과 같이 $x_t$에서 생성될 수 있다.
\[\begin{equation} I_{t-1} = I_t - (\bar{\alpha}_t - \bar{\alpha}_{t-1}) I_\textrm{res}^\theta - (\bar{\beta}_t - \sqrt{\bar{\beta}_{t-1}^2 - \sigma_t^2}) \epsilon_\theta + \sigma_t \epsilon_t \\ \textrm{where} \quad \epsilon_t \sim \mathcal{N} (0, I) \end{equation}\]$\eta = 0$, 즉 $\sigma_t = 0$이면, 결정론적 암시적 샘플링 방정식은 다음과 같다.
\[\begin{equation} I_{t-1} = I_t - (\bar{\alpha}_t - \bar{\alpha}_{t-1}) I_\textrm{res}^\theta - (\bar{\beta}_t - \bar{\beta}_{t-1}) \epsilon_\theta \end{equation}\]$\eta = 1$, 즉 $\sigma_t = 0$이면, 확률론적 perturbation 생성 방정식은 다음과 같다.
\[\begin{equation} I_{t-1} = I_t - (\bar{\alpha}_t - \bar{\alpha}_{t-1}) I_\textrm{res}^\theta - \frac{\beta_t^2}{\bar{\beta}_t} \epsilon_\theta + \frac{\beta_t \bar{\beta}_{t-1}}{\bar{\beta}_t} \epsilon_t \end{equation}\]3. Training Objective
DDPM과 DDIM은 noise만 추정하는 반면, RDDM은 residual $I_\textrm{res}^\theta$와 noise $\epsilon_\theta$를 모두 예측한다. 학습을 위해 다음과 같은 단순화된 loss function을 도출한다.
\[\begin{equation} L_\textrm{res} (\theta) := \mathbb{E} [\lambda_\textrm{res} \| I_\textrm{res} - I_\textrm{res}^\theta (I_t, t) \|^2] \\ L_\epsilon (\theta) := \mathbb{E} [\lambda_\epsilon \| \epsilon - \epsilon_\theta (I_t, t) \|^2] \end{equation}\]여기서 hyperparameter \(\lambda_\textrm{res}, \lambda_\epsilon \sim \{0, 1\}\)와 학습 입력 이미지는 $I_0$, $I_\textrm{res}$, $\epsilon$을 사용하여 합성된다. 실제로 $I_0를 $I_0 = I_\textrm{in} − I_\textrm{res}$로 대체할 수 있다.
\[\begin{equation} I_t = I_\textrm{in} + (\bar{\alpha}_t - 1) I_\textrm{res} + \bar{\beta}_t \epsilon \end{equation}\]샘플링 방법은 다음과 같이 3가지가 있다.
- $\lambda_\textrm{res} = 1$이고 $\lambda_\epsilon = 0$일 때 residual $I_\textrm{res}^\theta$는 네트워크에 의해 예측되는 반면 noise $\epsilon_\theta$는 $I_\textrm{res}^\theta$의 변환으로 표시된다.
- $\lambda_\textrm{res} = 0$이고 $\lambda_\epsilon = 1$일 때 noise $\epsilon_\theta$는 네트워크에 의해 예측되는 반면 residual $I_\textrm{res}^\theta$는 $\epsilon_\theta$의 변환으로 표시된다.
- $\lambda_\textrm{res} = 1$이고 $\lambda_\epsilon = 1$일 때 residual과 noise 모두 두 네트워크에 의해 예측된다.
두 번째 샘플링 방법은 noise만 추정하는 DDIM 및 DDPM과 유사하며 계수 schedule을 변환하여 DDPM 및 DDIM과 일치한다.
\[\begin{equation} \bar{\alpha}_t = 1 - \sqrt{\bar{\alpha}_\textrm{DDIM}^t} \quad \bar{\beta}_t = \sqrt{1 - \bar{\alpha}_\textrm{DDIM}^t}, \quad \sigma_t^2 = \sigma_t^2 (\textrm{DDIM}) \end{equation}\]Predicting Residual or Noise?
본 논문은 세 가지 샘플링 방법, 즉
- residual 예측 ($\lambda_\textrm{res} = 1$, $\lambda_\epsilon = 0$)
- noise 예측 ($\lambda_\textrm{res} = 0$, $\lambda_\epsilon = 1$)
- residual & noise 예측 ($\lambda_\textrm{res} = 1$, $\lambda_\epsilon = 1$)
을 제안하였다. 여기서는 실제 애플리케이션에 대한 최적의 샘플링 방법을 결정하는 것을 목표로 한다.

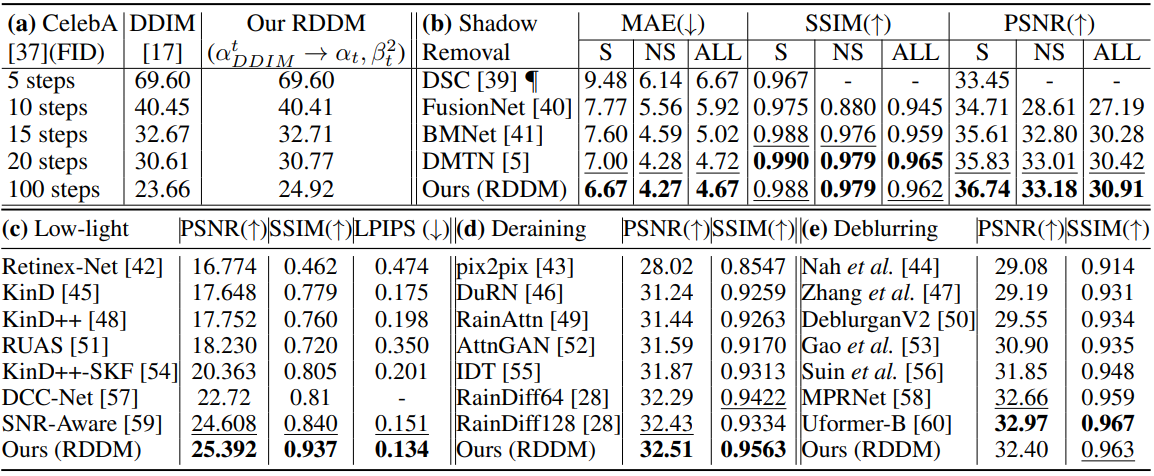
위 표는 noise 예측이 더 나은 FID와 IS의 이미지를 생성하지만 그림자 제거에는 효과적이지 않음을 보여준다. 이는 이미지 복원 task에서 $I_\textrm{res}^\theta$를 표현하기 위해 $\epsilon_\theta$를 사용하는 것이 부적절하기 때문일 수 있다. 반면, residual 예측은 그림자 제거에 대한 더 나은 결과를 보여 주지만 이미지 생성에 대한 FID는 더 나쁘다. 이러한 일관되지 않은 결과는 residual 예측이 확실성을 우선시하는 반면 noise 예측은 다양성을 강조한다는 사실에 기인한다. 저자들은 실험에서 이미지 생성을 위해 noise 예측을 사용하고 이미지 복원을 위해 residual & noise 예측을 사용하였다. 알려지지 않은 새로운 task에 대해 학습할 때 더 높은 확실성이 필요한 task에는 residual 예측을 사용하고 더 큰 다양성이 필요한 task에는 noise 예측을 사용하는 것이 좋다. 계산 리소스가 충분하면 noise 예측과 residual 예측을 위해 두 개의 개별 네트워크를 학습시키고 테스트 중에 최적의 샘플링 방법을 결정할 수 있다.
Experiments
- 데이터셋
- 이미지 생성: CelebA
- 그림자 제거: ISTD
- 저조도 향상: LOL
- deraining: RainDrop
- deblurring: GoPro
1. A Unified Diffusion Model for Image Generation and Restoration
다음은 이미지 생성과 복원에 대한 정량적 평가 결과이다.
다음은 이미지 생성과 복원에 대한 시각적 결과이다.

2. In-depth Analysis and Discussion
Decoupled Forward Diffusion Process
다음은 CelebA에서의 계수 schedule에 대한 정량적 비교 결과이다.
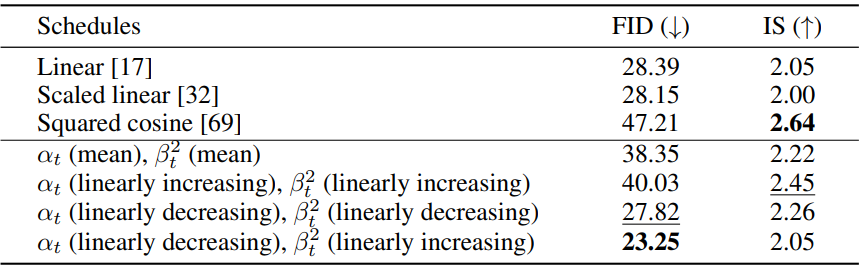
다음은 DDIM에서 RDDM으로의 계수 변환 결과이다.
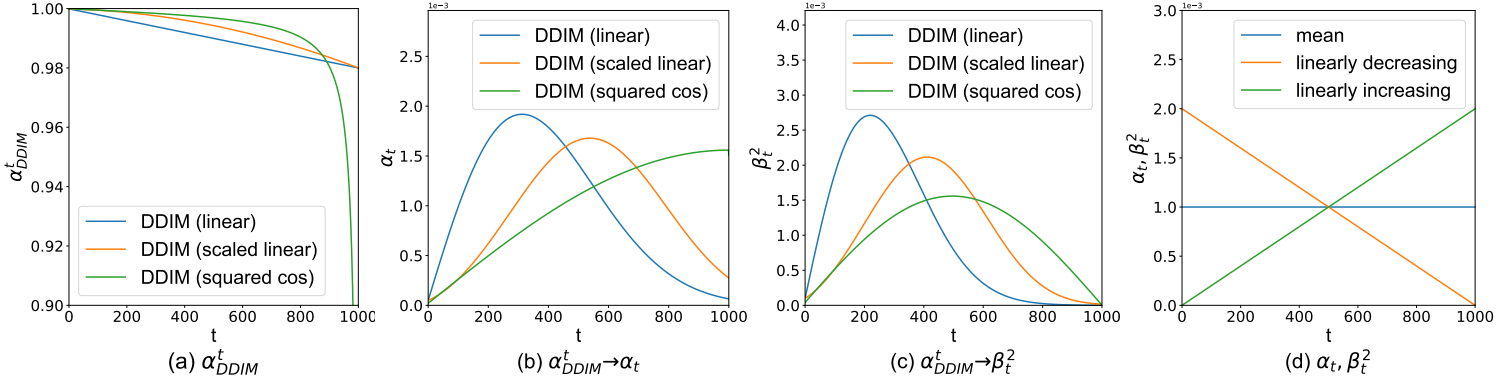
다음은 계수 schedule 재조정에 대한 분석 결과이다.

다음은 부분적으로 경로 독립적인 생성 프로세스에 대한 결과이다.
