[논문리뷰] Robust Classification via a Single Diffusion Model (RDC)
ICML 2024. [Paper] [Github]
Huanran Chen, Yinpeng Dong, Zhengyi Wang, Xiao Yang, Chengqi Duan, Hang Su, Jun Zhu
Tsinghua-Bosch Joint ML Center | Beijing Institute of Technology
24 May 2023
Introduction
딥러닝의 오랜 문제 중 하나는 딥러닝 모델이 잘못된 예측을 할 수 있는 적대적 예제에 대한 취약성으로, 인간이 감지할 수 없는 섭동을 추가하여 악의적으로 생성된다.
최근에 diffusion model은 Gaussian noise로 데이터를 점진적으로 교란시키는 forward process와 교란된 데이터에서 noise를 제거하는 방법을 학습하는 reverse process로 구성된 강력한 생성 모델로 등장했다. 일부 연구들은 다양한 방식으로 적대적 예제에 대한 robustness(견고성)를 개선하기 위해 diffusion model을 적용하려고 시도했다. 예를 들어, 적대적 이미지는 classifier에 공급되기 전에 diffusion model의 forward 및 reverse process를 통해 정제될 수 있다. 게다가 diffusion model에서 생성된 데이터는 adversarial training을 크게 개선하여 robustness 벤치마크에서 SOTA 결과를 얻을 수 있다. 이러한 연구들은 adversarial robustness 분야에서 diffusion model의 가능성을 보여주었다.
그러나 여전히 기존 방법의 몇 가지 제한 사항이 있다. 한편, diffusion 기반 정화 접근 방식은 일종의 기울기 난독화(gradient obfuscation)이며 정확한 기울기와 적절한 step 크기를 사용하여 효과적으로 공격할 수 있다. 저자들은 적대적 예시가 diffusion model이 다른 클래스의 이미지를 출력하도록 만들 수는 없지만 섭동이 완전히 제거되지는 않는다는 것을 관찰했다. 따라서 diffusion 기반 정화의 robustness가 좋지 않은 것은 주로 다운스트림 classifier의 취약성 때문이다. 반면, diffusion model에서 생성된 데이터를 사용하는 adversarial training 방법은 우수한 성능을 달성하지만 일반적으로 다양한 위협 모델에서 일반화할 수 없다.
요약하면, 이러한 방법은 diffusion model을 활용하여 판별적인 classifier의 robustness를 개선하지만 판별적 학습은 데이터 분포의 기본 구조를 캡처할 수 없으므로 학습 분포 밖의 입력 예측을 제어하기 어렵다. 생성적 접근 방식으로서 diffusion model은 전체 데이터 space에서 보다 정확한 score 추정이 가능하며 정확한 클래스 확률을 제공할 수도 있다. 따라서 diffusion model을 생성적 classifier로 변환하여 robustness를 개선하는 방법을 탐색한다.
본 논문에서는 adversarial robustness를 위해 기성 diffusion model에서 얻은 생성적 classifier인 Robust Diffusion Classifier (RDC)를 제안한다. 본 논문의 방법은 베이즈 정리를 통해 사전 분포가 $p(y)$인 diffusion model의 조건부 likelihood $p_\theta (x \vert y)$를 사용하여 클래스 확률 $p(y \vert x)$를 추정한다. 조건부 likelihood는 다양한 noise 레벨에서 모든 클래스에 대한 noise 예측 loss를 계산하는 변동 하한(VLB)에 의해 근사된다.
이론적으로 본 논문은 최적의 diffusion model이 일반적인 위협 모델에서 절대적인 robustness를 달성할 수 있음을 검증한다. 그러나 실제 diffusion model은 부정확한 밀도 추정 $p_\theta (x \vert y)$ 또는 likelihood와 해당 하한 사이의 큰 차이가 있어 성능이 저하될 수 있다. 이 문제를 해결하기 위해 diffusion classifier에 입력하기 전에 입력 데이터를 likelihood가 높은 영역으로 이동하는 사전 최적화 단계로 likelihood 최대화 방법을 제안한다. 따라서 RDC는 특정 적대적 공격에 대한 학습 없이 사전 학습된 diffusion model에서 직접 구성되어 다양한 위협 모델에서 robust classification을 수행할 수 있다.
Methodology

1. Preliminary: diffusion models
(자세한 내용은 DDPM 논문 리뷰 참고)
Forward process:
\[\begin{equation} q(x_t \vert x_0) = \mathcal{N} (x_t; \sqrt{\alpha_t} x_0, \sigma_t^2 I) \end{equation}\]Reverse process:
\[\begin{equation} p_\theta (x_{0:T}) = p(x_T) \prod_{t=1}^T p_\theta (x_{t-1} \vert x_t) \\ p_\theta (x_{t-1} \vert x_t) = \mathcal{N} (x_{t-1}; \mu_\theta (x_t, t), \tilde{\sigma}_t^2 I) \\ \mu_\theta (x_t, t) = \sqrt{\frac{\alpha_{t-1}}{\alpha_t}} \bigg( x_t - \sqrt{\frac{\sigma_t}{1 - \alpha_t}} \epsilon_\theta (x_t, t) \bigg) \end{equation}\]Diffusion loss:
\[\begin{equation} \mathbb{E}_{\epsilon, t} [w_t \| \epsilon_\theta (x_t, t) - \epsilon \|_2^2 ] \\ w_t = \frac{\sigma_t \alpha_{t-1}}{2 \tilde{\sigma}_t^2 (1 - \alpha_t) \alpha_t} = 1 \end{equation}\]조건부 생성:
\[\begin{equation} \mathbb{E}_{\epsilon, t} [w_t \| \epsilon_\theta (x_t, t, y) - \epsilon \|_2^2 ] \\ \epsilon_\theta (x_t, t) = \epsilon_\theta (x_t, t, y = \emptyset) \end{equation}\]2. Diffusion model for classification
입력 $x$가 주어지면 classifier는 모든 클래스 \(y \in \{1, 2, \cdots, K\}\)에 대한 확률 $p_\theta (y \vert x)$를 계산하고, $K$는 클래스의 수이며 가장 가능성 있는 클래스를
\[\begin{equation} \tilde{y} = \underset{y}{\arg \max} p_\theta (y \vert x) \end{equation}\]로 출력한다. 널리 사용되는 판별적 접근 방식은 조건부 확률 $p_\theta (y \vert x)$를 직접 학습하도록 CNN 또는 Vision Transformer를 학습시키지만, 학습 분포 밖에서 입력이 분류되는 방식을 제어하기 어렵기 때문에 $l_p$ norm 하에서 실제 예시 $x$에 가까운 적대적 예시 $x^\ast$에 대해
\[\begin{equation} \| x^\ast - x \|_p \le \epsilon_p \end{equation}\]로 정확하게 예측할 수 없다.
반면 diffusion model은 전체 데이터 space에 걸쳐 정확한 밀도 추정을 제공하도록 학습된다.
\[\begin{equation} p_\theta (y \vert x) \propto p_\theta (x \vert y) p(y) \end{equation}\]와 같은 베이즈 정리를 통해 diffusion model을 생성적 classifier로 변환함으로써 classifier가 데이터 space에서 더 정확한 조건부 확률 $p_\theta (y \vert x)$를 제공하여 더 나은 robustness로 이어진다. 본 논문에서는 단순화를 위해 균일한 prior $p(y) = 1 / K$를 가정하며, 이는 대부분의 데이터셋에 공통이다.
Log-likelihood와 diffusion loss 사이의 간격을 다음과 같이 정의한다.
\[\begin{equation} d(x, y, \theta) = \log p_\theta (x \vert y) + \mathbb{E}_{\epsilon, t} [w_t \| \epsilon_\theta (x_t, t, y) - \epsilon \|_2^2] \end{equation}\]$p(y) = 1 / K$이고 모든 $y$에 대해 $d(x, y, \theta) \rightarrow 0$이면, 조건부 확률 $p_\theta (y \vert x)$는 다음과 같이 계산할 수 있다.
\[\begin{equation} p_\theta (y \vert x) = \frac{\exp (- \mathbb{E}_{\epsilon, t} [w_t \| \epsilon_\theta (x_t, t, y) - \epsilon \|_2^2])}{\sum_{\hat{y}} \exp (- \mathbb{E}_{\epsilon, t} [w_t \| \epsilon_\theta (x_t, t, \hat{y}) - \epsilon \|_2^2])} \end{equation}\]$d(x, y, \theta)$가 0일 때 참인 diffusion loss를 사용하여 조건부 log-likelihood를 근사한다. 실제로 log-likelihood와 diffusion loss 사이에는 필연적으로 간격이 있지만 근사가 실험에서 잘 작동한다. 위 식은 랜덤 noise $\epsilon$과 timestep $t$에 대한 noise 예측 오차를 계산해야 한다. 게다가 본 논문의 방법은 $\log p(y)$에 의해 class $y$의 logit을 더하면 prior $p(y)$가 균일하지 않은 경우에도 적용할 수 있다. 여기서 $p(y)$는 학습 데이터에서 추정할 수 있다.
3. Robustness analysis under the optimal setting
$D$가 예시들의 집합이고 $D_y\subset D$를 ground-truth가 $y$인 예시들의 부분집합이라 하자. 최적의 diffusion model $\epsilon_{\theta_D^\ast} (x_t, t, y)$는 다음과 같다.
\[\begin{equation} \epsilon_{\theta_D^\ast} (x_t, t, y) = \sum_{x^{(i)} \in D_y} \frac{1}{\sigma_t} (x_t - \sqrt{\alpha_t} x^{(i)}) \cdot \textrm{softmax} \bigg( - \frac{1}{2 \sigma_t^2} \| x_t - \sqrt{\alpha_t} x^{(i)} \|_2^2 \bigg) \end{equation}\]최적의 diffusion model이 주어지면 최적의 diffusion classifier를 다음과 같이 쉽게 얻을 수 있다.
\[\begin{equation} p_{\theta_D^\ast} (y \vert x) = \textrm{softmax} (f_{\theta_D^\ast} (x)_y) \\ f_{\theta_D^\ast} (x)_y = - \mathbb{E}_{\epsilon, t} \bigg[ \frac{\alpha_t}{\sigma_t^2} \bigg\| \sum_{x^{(i)} \in D_y} s(x, x^{(i)}, \epsilon, t) (x - x^{(i)}) \bigg\|_2^2 \bigg] \end{equation}\]이다. 여기서 $s(x, x^{(i)}, \epsilon, t)$는 다음과 같다.
\[\begin{equation} s(x, x^{(i)}, \epsilon, t) = \textrm{softmax} \bigg( - \frac{1}{2 \sigma_t^2} \| \sqrt{\alpha_t} x + \sigma_t \epsilon - \sqrt{\alpha_t} x^{(i)} \|_2^2 \bigg) \end{equation}\]직관적으로 최적의 diffusion classifier는 클래스 $y$의 입력 예제 $x$와 실제 예제 $x^{(i)}$ 사이의 가중 평균 차이의 $l_2$ norm을 활용하여 $x$에 대한 logit을 계산한다. Classifier는 입력 $x$가 $D_{\tilde{y}}$에 속한 실제 예시에 더 근접한 경우 입력 $x$에 대한 레이블 $\tilde{y}$를 예측한다. 또한, $l_2$ norm은 가중치 $\alpha_t / \sigma_t^2$로 $t$에 대해 평균화된다. $\alpha_t / \sigma_t^2$가 $t$에 대해 단조롭게 감소하기 때문에 classifier는 noisy한 예제에 대해 작은 가중치를 부여하고 깨끗한 예제에 대해 큰 가중치를 부여한다. 이는 noisy한 예제가 classification에서 중요한 역할을 하지 않기 때문에 합리적이다.
4. Likelihood maximization
앞서 언급한 문제를 해결하기 위한 간단한 접근 방식은 diffusion model이 정확한 밀도 추정을 제공할 수 없거나 $d(x, y, \theta)$가 큰 영역에서 입력이 벗어날 수 있도록 $x$에 대해 diffusion loss \(\mathbb{E}_{\epsilon, t} [w_t \| \epsilon_\theta (x_t, t, y) - \epsilon \|_2^2 ]\)를 최소화하는 것이다. 그러나 $x$의 ground-truth 레이블을 알지 못하므로 최적화가 불가능하다. 대체 전략으로 unconditional diffusion loss를 최소화한다.
\[\begin{equation} \min_{\hat{x}} \mathbb{E}_{\epsilon, t} [w_t \| \epsilon_\theta (\hat{x}_t, t) - \epsilon \|_2^2 ], \quad \textrm{s.t. } \| \hat{x} - x \|_\infty \le \eta \end{equation}\]여기서 최적화된 입력 $\hat{x}$와 원래 입력 $x$ 사이의 $l_\infty$ norm을 $\eta$보다 작게 제한하여 $\hat{x}$를 다른 클래스의 영역으로 최적화하는 것을 방지한다. 위 식이 실제로 log-likelihood의 하한을 최대화하므로 이 접근 방식을 Likelihood Maximization이라고 한다.
위 식을 풀면 최적화된 입력 $\hat{x}$는 더 높은 log-likelihood를 가지게 되며, 이는 $\hat{x}$가 실제 데이터에 더 가깝다는 것을 나타낸다. 이 방법은 입력을 정화하는 것으로도 이해할 수 있다. 게다가, 적대적 예시는 일반적으로 ground-truth 클래스 $y$에 해당하는 실제 예시 근처에 있기 때문에 더 높은 $\log p(x)$ 방향을 따라 이동하면 아마도 더 높은 $\log p(x \vert y)$로 이어질 것이다. 따라서 $\hat{x}$는 diffusion classifier에 의해 보다 정확하게 분류될 수 있다. Likelihood Maximization은 적대적인 noise를 제거하는 것을 목표로 하기 때문에 다른 diffusion 기반 정화 접근 방식과 다르다. 그러나 diffusion classifier로 쉽게 분류할 수 있도록 높은 log-likelihood를 향해 데이터를 최적화하는 것을 목표로 한다. 기울기 방향을 안정화하고 바람직하지 않은 극소점을 피하기 위해 momentum optimizer로 위 식을 푼다.
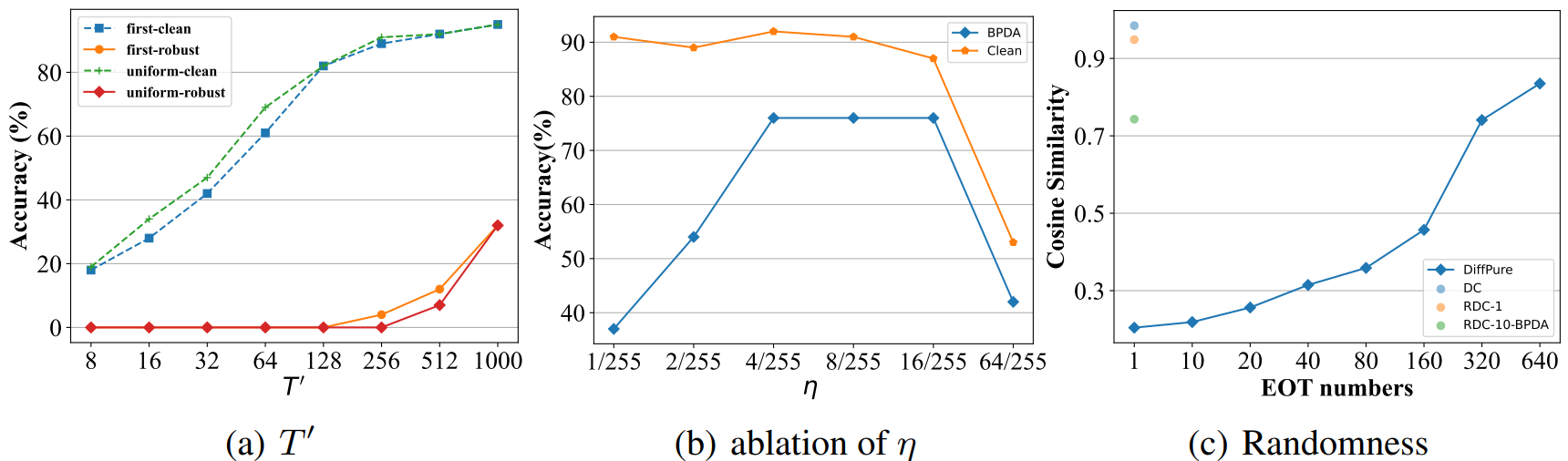
5. Variance reduction
$\epsilon$과 $t$의 expectation에 대한 diffusion loss를 추정하기 위한 일반적인 방법은 몬테카를로 샘플링을 사용하는 것이다. 이 샘플링은 적은 샘플로 높은 분산, 많은 샘플로 높은 시간 복잡도로 이어진다. 저렴한 계산 비용으로 분산을 줄이기 위해 $t$를 샘플링하는 대신 $t$에 대한 expectation을 다음과 같이 직접 계산한다.
\[\begin{equation} \mathbb{E}_{\epsilon, t} [w_t \| \epsilon_\theta (x_t, t, y) - \epsilon \|_2^2 ] = \frac{1}{T} \sum_{t=1}^T \mathbb{E}_\epsilon [w_t \| \epsilon_\theta (x_t, t, y) - \epsilon \|_2^2 ] \end{equation}\]위 식은 모든 timestep에 대한 noise 예측 오차를 계산해야 한다. $\epsilon$의 경우 여전히 몬테카를로 샘플링을 사용하지만 좋은 성능을 달성하려면 $\epsilon$ 하나만 샘플링해도 충분하다. 따라서 diffusion classifier는 diffusion model에서 비롯된 RDC의 주요 한계로 판별적 classifier보다 계산 비용이 더 많이 드는 diffusion model의 $K \times T$개의 forward pass가 필요하다. 일정한 간격으로 timestep을 선택하는 체계적인 샘플링을 통해 timestep의 수를 더 줄일 수 있다. Clean accuracy가 명백하게 하락하지는 않지만 timestep 수를 줄인 후 목적 함수가 더 이상 log-likelihood와 강한 상관 관계가 없기 때문에 robust accuracy에 상당한 영향을 미친다. RDC의 전체 알고리즘은 Algorithm 1에 요약되어 있다.

Experiments
- 데이터셋: CIFAR-10
- 학습 디테일: NCSN++ 아키텍처 (classifier-free guidance)
- Hyperparameters
- 최적화 step $N = 10$
- Momentum decay factor $\mu = 1$
- $\eta = 8/255$
- Step size $\gamma = \eta / N$
- Robustness 평가
- AutoAttack 사용
- $l_\infty$ norm: $\epsilon_\infty = 8 / 255$
- $l_2$ norm: $\epsilon_2 = 0.5$
1. Comparison with the state-of-the-art
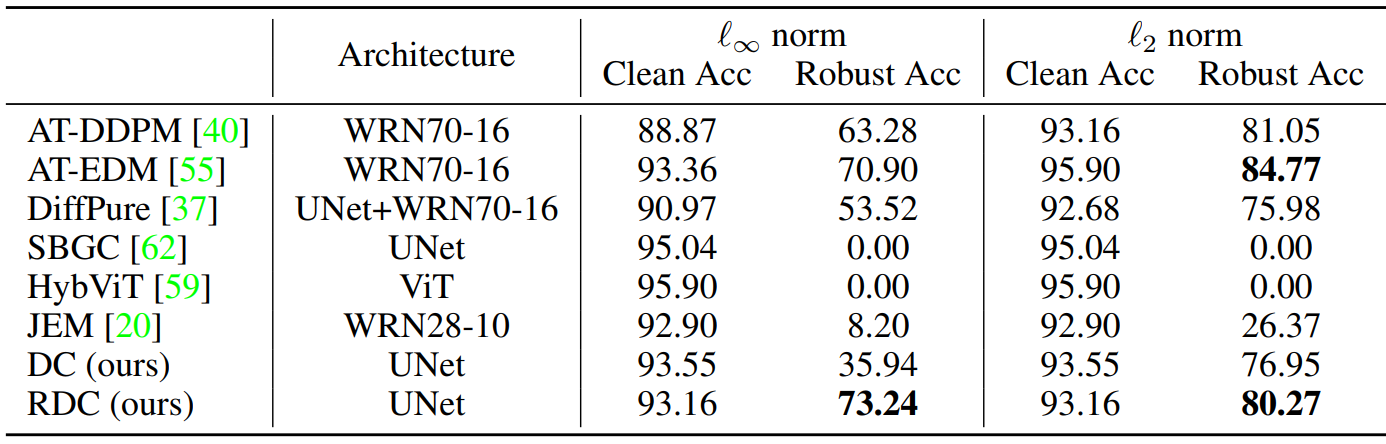
2. Defense against unseen threats
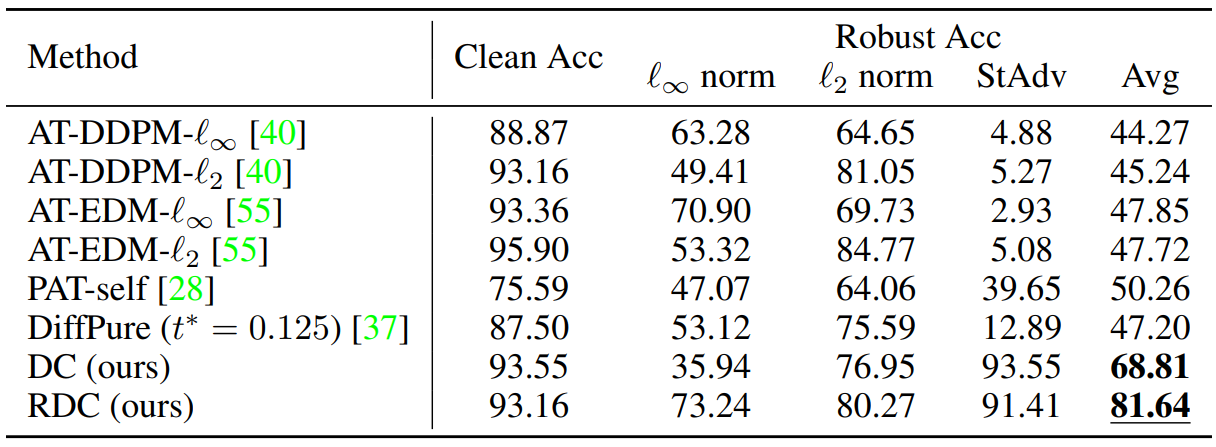
3. Evaluation of gradient obfuscation

4. Ablation studies