[논문리뷰] Relaxing Accurate Initialization Constraint for 3D Gaussian Splatting (RAIN-GS)
arXiv 2024. [Paper] [Page] [Github]
Jaewoo Jung, Jisang Han, Honggyu An, Jiwon Kang, Seonghoon Park, Seungryong Kim
Korea University
14 Mar 2024

Introduction
Novel view synthesis는 일련의 이미지가 주어지면 3D 장면의 새로운 뷰를 렌더링하는 것을 목표로 하는 task이다. NeRF는 이미지에서만 복잡한 3D 형상과 반사 효과를 캡처하는 implicit한 표현을 학습하여 이 분야에서 놀라운 성공을 거두었다. 그러나 NeRF가 MLP에 의존하면 속도가 느리고 계산 집약적인 볼륨 렌더링이 발생하여 실시간 응용이 어렵다.
최근 3D Gaussian splatting(3DGS)이 고품질 결과와 실시간 렌더링을 위한 강력한 대안으로 등장했다. NeRF의 implicit한 표현과 달리 3DGS는 explicit한 3D Gaussian을 사용하여 장면을 모델링한다. 또한 효율적인 CUDA 기반 미분 가능한 타일 rasterization 기술을 통해 학습된 3D Gaussian을 실시간으로 렌더링할 수 있다.
놀라운 결과에도 불구하고 3DGS는 Structure-from-Motion(SfM)에서 얻은 결과 대신 랜덤하게 초기화된 포인트 클라우드로 학습할 때 상당한 성능 저하를 나타낸다. 이러한 제한은 대칭, 반사 속성, 텍스처 없는 영역이 있는 장면, 사용 가능한 뷰가 제한된 장면과 같이 SfM 기술이 수렴하는 데 어려움을 겪는 시나리오에서 특히 두드러진다. 또한 초기 포인트 클라우드에 대한 3DGS의 의존성으로 인해 SfM은 외부 센서 또는 미리 calibration된 카메라를 통해 카메라 포즈를 얻을 수 있는 상황에서도 어려운 전제 조건이 된다.
본 논문에서는 “3D Gaussian splatting에서 초기 포인트 클라우드가 왜 그렇게 중요한가?”라는 자연스러운 질문에서 시작하였으며, SfM과 랜덤하게 초기화된 포인트 클라우드 간의 차이를 분석하였다. 저자들은 렌더링된 이미지의 주파수 도메인 신호를 분석하고 SfM 초기화가 실제 분포의 대략적인 근사치로 시작하는 것으로 해석될 수 있음을 발견했다. 3DGS에서 이 대략적인 근사치는 최적화 프로세스 전반에 걸쳐 후속 개선을 위한 기반 역할을 하여 Gaussian이 local minima에 빠지는 것을 방지한다.
이 분석을 바탕으로 저자들은 단순화된 1D regression task의 toy experiment를 수행하여 Gaussian이 처음부터 ground truth 분포를 강력하게 학습하도록 가이드하는 필수 요소를 식별하였다. 이 실험은 실제 분포의 대략적인 근사치(저주파 성분)를 초기에 학습하는 것이 성공적인 재구성을 위해 중요하다는 것을 보여준다. SfM 초기화와 유사하게, 처음에 학습된 대략적인 근사치는 분포의 고주파 성분을 학습할 때 guidance 역할을 한다.
이러한 관찰을 확장하여 본 논문은 Relaxing Accurate INitialization Constraint for 3D Gaussian Splatting (RAIN-GS)이라는 새로운 최적화 전략을 제안하였다. 이 전략은 분산이 큰 sparse한 Gaussian으로 시작하는 새로운 초기화 방법과 렌더링 프로세스에서의 점진적인 Gaussian low-pass filtering을 결합한다. 이 전략은 3D Gaussian이 먼저 대략적인 분포를 학습하고 나중에 나머지 고주파 성분을 강력하게 학습하도록 성공적으로 가이드한다는 것을 보여준다. 이 간단하면서도 효과적인 전략은 정규화, 학습, 또는 외부 모델 없이 랜덤하게 초기화된 포인트 클라우드에서 시작할 때의 결과를 크게 향상시켜 SfM에서 정확하게 초기화된 포인트 클라우드의 필요를 효과적으로 완화한다.
Motivation
1. SfM initialization in 3DGS
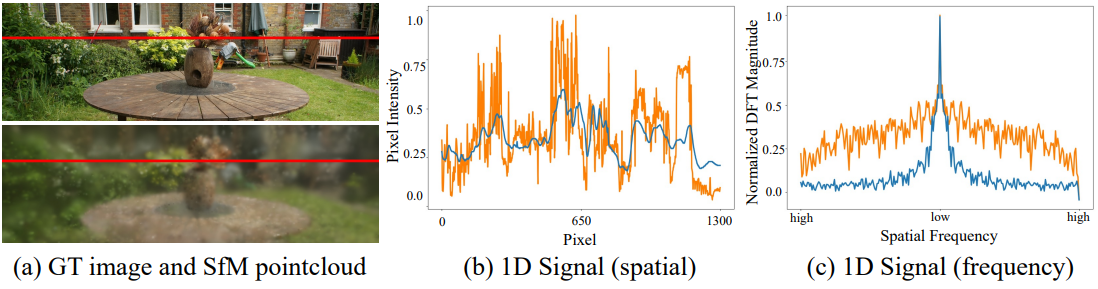
저자들은 포인트 클라우드의 다양한 초기화에 따른 3DGS의 큰 성능 격차를 이해하기 위해 먼저 SfM 포인트 클라우드를 사용하여 학습할 때의 동작을 분석하였다. SfM은 색상과 위치에 대한 대략적인 정보가 포함된 sparse한 포인트 클라우드를 제공한다. 3DGS는 이 결과를 효과적으로 활용하여 Gaussian 파라미터 $\mu_i$와 spherical harmonics (SH) 계수를 포인트 클라우드 위치와 색상으로 초기화한다. 이러한 초기화의 장점은 위 그림의 (a)에서 분명하게 드러난다. 단 10 step (전체 학습 step의 0.03%) 후에 렌더링된 결과는 이미 합리적인 품질과 실제 이미지와 유사성을 나타낸다.
저자들은 SfM 초기화의 이점을 더 자세히 조사하기 위해 푸리에 변환을 사용하여 주파수 도메인에서 렌더링된 이미지를 분석하였다. 위 그림에서는 (a)에서 빨간색으로 표시된 것처럼 실제 이미지와 렌더링된 이미지 모두에서 수평선을 랜덤하게 선택한다. 이 선을 따른 픽셀 강도 값은 (b)에 시각화되어 있으며 GT 이미지는 주황색이고 렌더링된 이미지는 파란색이다. 그런 다음 이러한 신호는 주파수 도메인으로 변환되어 (c)에 표시된다. 주파수 도메인에서의 이 분석은 SfM 초기화가 기본 분포의 대략적인 근사치를 제공한다는 것을 보여준다.
Novel view synthesis의 목표는 장면의 3D 분포를 이해하는 것이므로 실제 분포의 저주파 및 고주파 성분을 모두 모델링하는 것이 필요하다. 이를 가능하게 하기 위해 NeRF는 위치 인코딩을 활용하여 고주파 성분의 학습을 촉진한다. 그러나 고주파 성분의 지나치게 빠른 수렴은 NeRF가 저주파 성분을 탐색하는 것을 방해하여 NeRF가 고주파 아티팩트에 overfitting되도록 만든다. 이 문제를 피하기 위해 이전 연구들에서는 NeRF가 저주파 성분을 먼저 충분히 탐색하도록 가이드하는 주파수 어닐링 전략을 채택했다.
이러한 관점에서 SfM 초기화부터 시작하는 것은 이미 저주파 성분을 제공하므로 유사한 프로세스를 따르는 것으로 이해될 수 있다. 이 분석을 확장하여 랜덤하게 초기화된 포인트 클라우드로 시작할 때 강력한 학습을 활성화하려면 3DGS가 저주파 성분을 먼저 학습하도록 가이드할 수 있는 유사한 전략이 필수적이다.
2. Dense random initialization in 3DGS
본 논문은 SfM에서 초기화된 포인트 클라우드를 사용할 수 없는 상황에 대해 dense-small-variance (DSV) 랜덤 초기화 방법을 제안하였다. 카메라 bounding box 크기의 3배인 큐브 내에서 dense한 포인트 클라우드를 랜덤하게 샘플링한다. 초기 공분산은 가장 가까운 세 개의 이웃 지점까지의 평균 거리로 정의되므로 작은 분산으로 dense한 3D Gaussian을 초기화하게 된다.
저자들은 저주파 우선 학습의 중요성을 토대로 DSV 초기화가 최적화 프로세스에 어떻게 영향을 미치는지 조사하기 위해 단순화된 1D regression task에서 toy experiment를 수행하였다. 1D Gaussian을 사용하면 초기화 효과를 격리하는 제어된 환경을 제공할 수 있다. 구체적으로, 랜덤 1D 신호 $Y(x)$를 실제 분포로 모델링하기 위한 학습 가능한 파라미터로 평균 $\mu_i$와 분산 $\sigma_i^2$를 사용하여 1D Gaussian을 정의한다. $N$개의 Gaussian을 학습 가능한 가중치 $w_i$와 혼합함으로써 다음과 같이 혼합된 신호와 $Y(x)$ 사이의 L1 loss로 파라미터를 학습시킨다.
\[\begin{equation} \mathcal{L} = \sum_x \bigg\| Y(x) - \sum_{i=0}^N w_i \cdot \exp \bigg( - \frac{(x - \mu_i)^2}{2 \sigma_i^2} \bigg) \bigg\| \end{equation}\]여기서 DSV 초기화의 경우 $N = 1,000$으로 설정한다.
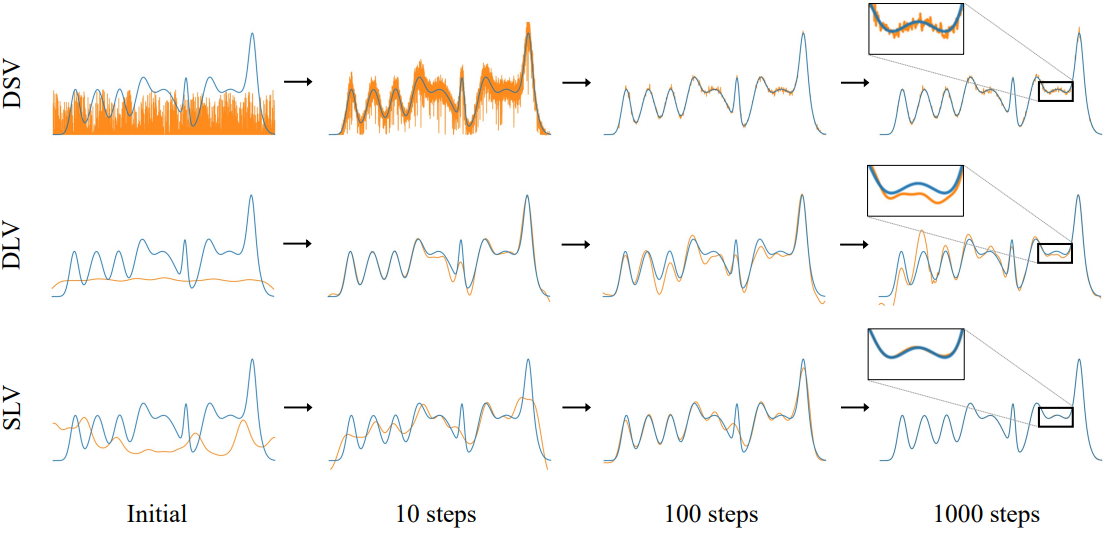
위 그림의 맨 윗줄과 같이 DSV 랜덤 초기화를 사용한 학습은 고주파에서 지나치게 빠른 수렴 경향을 나타낸다. 이는 단 10 step 후에 고주파 성분을 포착하는 모델의 능력에서 분명하게 드러난다. 그러나 이렇게 고주파에 빠르게 초점을 맞추면 최종 재구성에서 원치 않는 고주파 아티팩트가 발생한다. 저자들은 이런 현상이 dense한 Gaussian의 작은 초기 분산에서 발생한다고 가정하였다. 이는 각 Gaussian이 매우 국지적인 영역을 모델링하도록 제한하여 overfitting에 대한 민감성을 증가시킨다.
저자들은 가설을 검증하기 위해 초기 분산에 값 $s$를 추가하여 초기화를 dense-large variance (DLV)로 변경하여 실험을 반복하였다. 이 수정은 Gaussian이 더 넓은 영역에서 학습하도록 효과적으로 장려한다. 그 결과(중간 행)는 저자들의 가설을 뒷받침한다. 10 step에서 학습된 신호는 DSV 초기화와 비교할 때 저주파 성분을 우선한다는 점을 보여준다. 그러나 $w_i = 0$으로 학습된 가중치를 통해 Gaussian을 제거하는 능력이 있어도 dense한 초기화로 인해 학습된 신호에 변동이 발생하여 1,000 step 후에 수렴이 방지된다. 저주파 성분에 높은 우선순위를 두려면 더 넓은 영역(큰 분산)에서 학습하는 것이 필요하지만 dense한 초기화는 여전히 불안정성과 수렴 문제로 이어질 수 있다.
Methodology
1. Sparse-large-variance (SLV) initialization
1D toy experiment에서 입증된 것처럼 dense한 초기화의 최적화는 목표 분포를 충실하게 모델링하는 데 실패한다. 여기서 DLV는 원하지 않는 고주파 아티팩트를 생성하고 DSV는 저주파 성분을 먼저 학습하는 데 성공했지만 수렴에 실패한다.
본 논문은 두 가지 문제를 모두 해결하기 위해 sparse-large-variance (SLV) 초기화를 제안하였다. Sparsity는 최적화 전반에 걸쳐 변동을 줄이는 반면, 큰 분산은 저주파 분포에 대한 초기 집중을 보장한다. 여기서 실험은 초기 분산에 $s$를 추가하여 $N = 15$개의 Gaussian으로 반복된다. SLV 초기화는 10 step에서 저주파 성분의 높은 우선순위 지정과 1,000 step 이후 오차를 최소화한 실제 분포 모델링에 모두 성공한다.
따라서 카메라 bounding box 크기의 3배로 정의된 동일한 볼륨에서 랜덤한 점을 초기화하더라도 훨씬 더 sparse한 3D Gaussian 집합을 초기화한다. 3D Gaussian의 초기 공분산은 가장 가까운 세 이웃의 거리를 기반으로 정의되므로 sparse한 초기화는 더 큰 초기 공분산으로 이어져 각 Gaussian이 장면의 더 넓은 영역을 모델링하도록 장려한다.
$N$개의 포인트를 초기화할 때 DSV 초기화는 원래 10만보다 큰 $N$을 선택한다. 저자들의 분석에 맞춰 이 값을 낮추면 저주파 성분에 대한 초기 집중을 장려하여 고주파 아티팩트가 줄어들어 성능이 크게 향상된다. 놀랍게도 이 전략은 극도로 sparse한 초기화(ex. $N = 10$만큼 낮음)에서도 더욱 효과적이 되어 새로운 SLV 초기화 방법의 효율성을 검증한다. 아래 그림에는 다양한 초기화 방법에 대한 예시가 나와 있다.

2. Progressive Gaussian low-pass filter control
SLV 초기화 방법은 효과적이지만 여러 densification 단계 후에 3D Gaussian 수가 기하급수적으로 증가하여 DSV 초기화와 유사한 문제가 발생하는 경향이 있다. 3D Gaussian을 정규화하여 학습 초기 단계에서 저주파 성분을 충분히 탐색하기 위해 본 논문은 렌더링 단계에서 활용되는 Gaussian low-pass filter의 새로운 점진적 제어를 제안하였다.
구체적으로, 3DGS의 렌더링 단계에서 3D Gaussian $G_i$로부터 투영된 2D Gaussian $G_i^\prime$은 다음과 같이 정의된다.
\[\begin{equation} G_i^\prime (x) = \exp ( - \frac{1}{2} (x - \mu_i^\prime)^\top \Sigma_i^{\prime -1} (x - \mu_i^\prime) ) \end{equation}\]그러나 투영된 2D Gaussian을 직접 사용하면 픽셀보다 작아지면 시각적 아티팩트가 발생할 수 있다. 적어도 한 픽셀의 커버리지를 보장하기 위해 다음과 같이 공분산의 대각 성분에 작은 값을 추가하여 2D Gaussian의 스케일을 확대한다.
\[\begin{equation} G_i^\prime (x) = \exp ( - \frac{1}{2} (x - \mu_i^\prime)^\top (\Sigma_i^\prime + sI)^{-1} (x - \mu_i^\prime) ) \end{equation}\]여기서 $s = 0.3$은 미리 정의된 값이고 $I$는 단위 행렬이다. 이 프로세스는 투영된 2D Gaussian $G_i^\prime$과 Gaussian low-pass filter $h$(평균 $\mu = 0$, 분산 $\sigma^2 = 0.3$) 사이의 convolution $G_i^\prime \otimes h$로 해석될 수도 있다. 이는 앨리어싱을 방지하기 위한 필수 단계이다. Low-pass filter를 사용한 convolution 후 투영된 Gaussian $G_i^\prime$의 영역은 2D 공분산 행렬 $(\Sigma_i^\prime + sI)$의 더 큰 고유값의 3배로 정의된 반경을 갖는 원으로 근사화된다. 아래 그림은 (a)에 비해 (b)에서 투영된 Gaussian 더 넓은 영역으로 분산되는 low-pass filter의 효과를 보여준다.
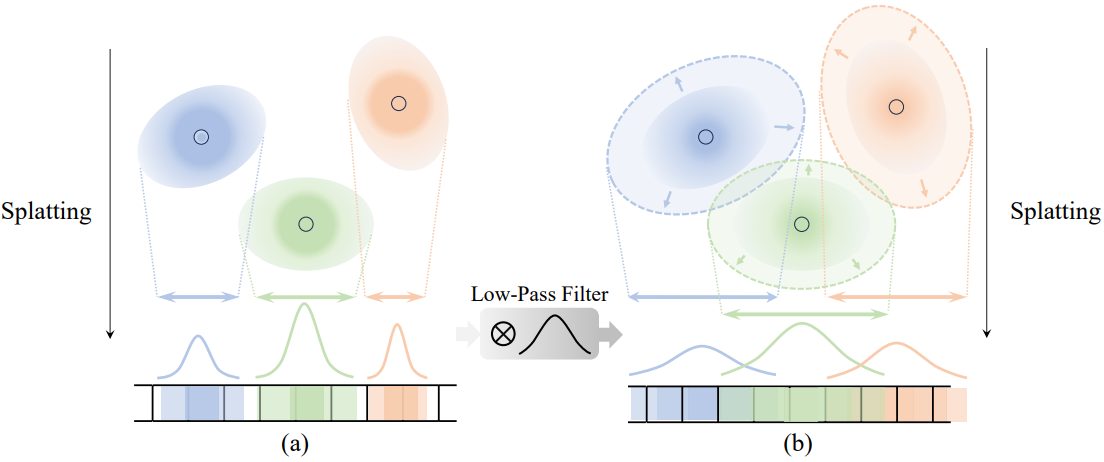
저자들은 전체 최적화 프로세스를 통해 고정된 값 $s$를 사용하는 대신 이 $s$가 화면 공간에서 각 Gaussian이 처리해야 하는 최소 영역을 보장할 수 있음을 확인했다. 더 넓은 영역에서 학습하는 것이 저주파 성분을 우선시한다는 앞의 분석을 기반으로 Gaussian을 정규화하여 학습 초기 단계에서 넓은 영역을 다루고 더 많은 로컬 영역에서 점진적으로 학습하도록 제어한다. 구체적으로, 값 $s$는 투영된 Gaussian 영역이 $9\pi s$보다 커지도록 보장하므로 $s = HW / 9 \pi N$이 되도록 $s$의 값을 정의한다. 여기서 $N$은 iteration에 따라 달라질 수 있는 Gaussian 수를 나타내고 $H$와 $W$는 각각 이미지의 높이와 너비이다. Gaussian의 수는 iteration이 진행됨에 따라 변동될 수 있지만 Gaussian이 기하급수적으로 증가하는 경향이 있으므로 이 전략을 점진적인 Gaussian low-pass filter 제어라고 부른다. SLV 랜덤 초기화와 점진적인 low-pass filter 제어를 모두 활용하는 것이 3D Gaussian이 저주파 성분을 먼저 학습하도록 강력하게 가이드하는 데 중요하다.
Experiments
- 데이터셋: Mip-NeRF360, Tanks&Temples, Deep Blending
- 구현 디테일
- 초기 Gaussian 수 $N = 10$
- $s = \min (\max (HW / 9 \pi N, 0.3), 300.0)$ (1,000 step마다 갱신)
- 최대 SH degree: 3
- 5,000 step 이후 1,000 step마다 SH degree를 증가
- Gaussian divide factor: 원래 1.6에서 1.4로 줄임
1. Qualitative and quantitative comparison
다음은 이전 방법들과 Mip-NeRF360에서 비교한 결과이다.
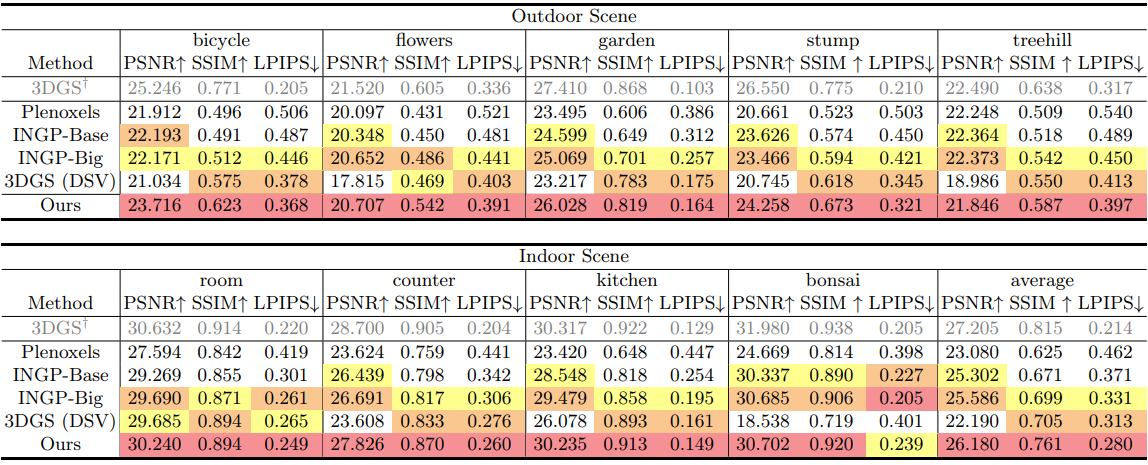

다음은 이전 방법들과 Tanks&Temples와 Deep Blending에서 비교한 결과이다.
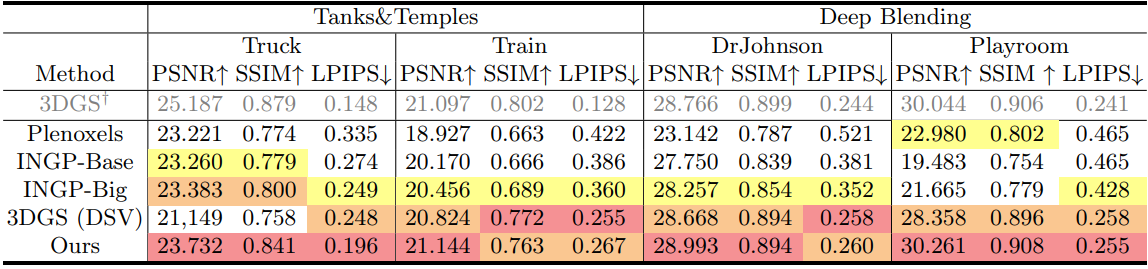

2. Ablation studies
다음은 주요 구성 요소에 대한 ablation study 결과이다.
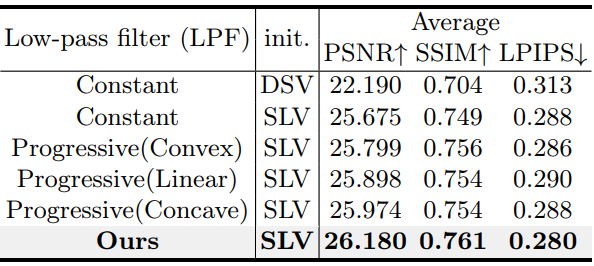
다음은 $N$에 대한 ablation study 결과이다.
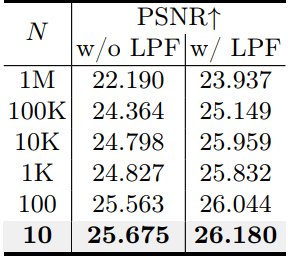
3. 3DGS in sparse view settings
다음은 sparse view setting에서의 결과이다.

