[논문리뷰] Retrieval-Augmented Generation for Knowledge-Intensive NLP Tasks
NeurIPS 2020. [Paper] [Page] [Github]
Patrick Lewis, Ethan Perez, Aleksandra Piktus, Fabio Petroni, Vladimir Karpukhin, Naman Goyal, Heinrich Küttler, Mike Lewis, Wen-tau Yih, Tim Rocktäschel, Sebastian Riedel, Douwe Kiela
Facebook AI Research | University College London | New York University
22 May 2020
Introduction
사전 학습된 언어 모델은 데이터에서 상당한 양의 지식을 학습하며, 외부 메모리에 액세스하지 않고도 implicit한 parametric memeory로 이를 수행할 수 있다. 이러한 모델들은 메모리를 쉽게 확장하거나 수정할 수 없고 예측에 대한 통찰력을 간단하게 제공할 수 없으며 “hallucination”을 유발할 수 있다. Parametric memory와 non-parametric (즉, 검색 기반) memory를 결합하는 하이브리드 모델은 지식을 직접 수정하고 확장할 수 있고 액세스한 지식을 검사하고 해석할 수 있기 때문에 이러한 문제 중 일부를 해결할 수 있다. 본 논문에서는 이러한 하이브리드 모델을 sequence-to-sequence (seq2seq) 모델에 적용하였다.
본 논문은 retrieval-augmented generation (RAG)이라고 하는 범용 fine-tuning 방법을 통해 사전 학습된 생성 모델에 non-parametric memeory를 부여하였다. 저자들은 사전 학습된 seq2seq transformer를 parametric memory로 하고, 사전 학습된 retriever로 엑세스하는 위키피디아의 dense한 벡터 인덱스를 non-parametric memory로 하여 RAG 모델을 구축하였다. 그런 다음 이러한 구성 요소들을 end-to-end로 fine-tuning하였다.
Retriever는 입력을 조건으로 latent 문서를 제공하고, seq2seq 모델은 입력과 latent 문서를 조건으로 출력을 생성한다. 저자들은 latent 문서를 top-K 근사로 marginalize하였다. 이 때, 동일한 문서가 모든 토큰을 담당한다고 가정하면 per-output basis로 marginalize하고, 서로 다른 문서가 서로 다른 토큰을 담당한다고 가정하면 per-token basis로 marginalize한다. T5나 BART와 마찬가지로 RAG는 모든 seq2seq task에서 fine-tuning할 수 있으며, generator와 retriever가 공동으로 학습된다.
Non-parametric memory를 활용하는 기존 방법들은 특정 task를 위해 처음부터 학습된다. 반면, RAG는 parametric memory와 non-parametric memeory가 모두 사전 학습되기 때문에 추가 학습 없이도 엑세스 메커니즘을 사용함으로써 지식에 접근할 수 있다.
RAG는 지식 집약적인 task에서 이점이 있으며, 이러한 task들은 외부 지식 소스에 대한 접근 없이는 합리적으로 수행할 수 없다. RAG 모델은 Natural Questions, WebQuestions, CuratedTrec에서 SOTA 결과를 달성하였으며, TriviaQA에서 특수한 목적 함수를 사용하는 최근 방법보다 훨씬 우수한 성과를 보였다. 지식 집약적 생성의 경우, MS-MARCO와 Jeopardy Quesion Generation에서 BART보다 더 사실적이고 구체적이며 다양한 응답을 생성하였다. FEVER 사실 검증의 경우, 강력한 supervision을 사용하는 SOTA 모델과 4.3% 이내의 결과를 달성하였다. 마지막으로, 저자들은 non-parametric memeory를 대체하여 세상이 변화함에 따라 모델의 지식을 업데이트할 수 있음을 보여주었다.
Methods
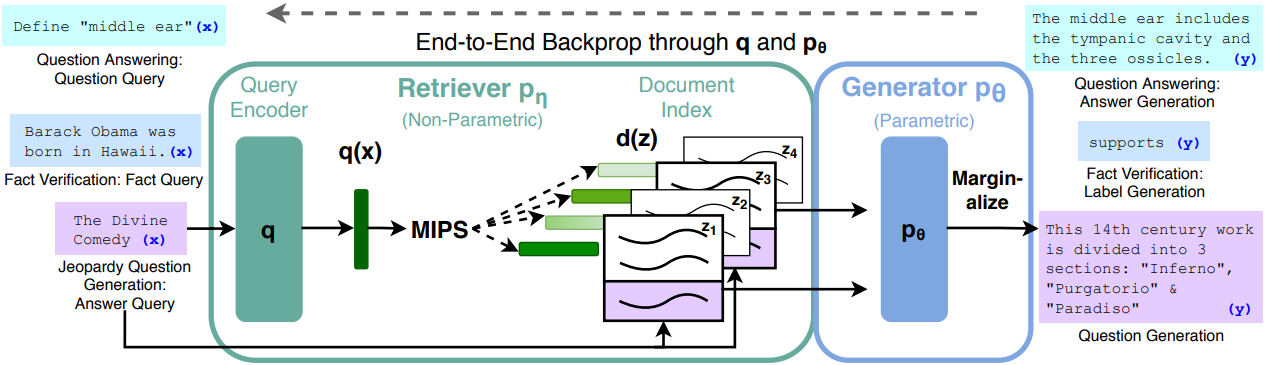
RAG 모델은 입력 시퀀스 $x$를 사용하여 텍스트 문서 $z$를 검색하고 추가 컨텍스트로 이를 사용하여 타겟 시퀀스 $y$를 생성한다. 모델은 두 가지 구성 요소를 활용한다.
- Retriever $p_\eta (z \vert x)$: 파라미터가 $\eta$이며, 주어진 쿼리 x에 대하여 텍스트 구절에 대한 분포를 반환한다.
- Generator $p_\theta (y_i \vert x, z, y_{1:i−1})$: 이전 토큰들 $y_{1:i−1}$, 원래 입력 $x$, 검색된 구절 $z$의 컨텍스트를 기반으로 현재 토큰 $y_i$를 생성한다.
Retriever와 generator를 end-to-end로 학습시키기 위해 검색된 문서를 latent variable로 취급한다. 저자들은 생성된 텍스트에 대한 분포를 생성하기 위해 latent 문서를 다른 방식으로 marginalize하는 두 가지 모델을 제안하였다.
- RAG-Sequence: 동일한 문서를 사용하여 각 대상 토큰을 예측한다.
- RAG-Token: 다른 문서를 기반으로 각 대상 토큰을 예측한다.
1. Models
RAG-Sequence
RAG-Sequence 모델은 검색된 동일한 문서를 사용하여 전체 시퀀스를 생성한다. 검색된 문서를 하나의 latent variable로 취급하여 top-K 근사를 통해 seq2seq 확률 $p(y \vert x)$를 얻는다. 구체적으로, 상위 $K$개의 문서는 retriever를 사용하여 검색되고 generator는 각 문서에 대한 출력 시퀀스 확률을 생성한 다음 이를 marginalize한다.
\[\begin{aligned} p_\textrm{RAG-Sequence} (y \vert x) &\approx \sum_{z \in \textrm{top-k}(p(\cdot \vert x))} p_\eta (z \vert x) p_\theta (y \vert x, z) \\ &= \sum_{z \in \textrm{top-k}(p(\cdot \vert x))} p_\eta (z \vert x) \prod_i^N p_\theta (y_i \vert x, z, y_{1:i-1}) \end{aligned}\]RAG-Token
RAG-Token 모델은 각 대상 토큰에 대해 다른 latent 문서를 사용하여 그에 따라 marginalize할 수 있다. 이를 통해 generator는 답변을 생성할 때 여러 문서에서 콘텐츠를 선택할 수 있다. 구체적으로, 상위 $K$개의 문서는 retriever를 사용하여 검색되고, generator는 marginalize하기 전에 각 문서에 대한 다음 출력 토큰에 대한 분포를 생성하고, 이 프로세스를 그 다음 출력 토큰에 대하여 반복한다.
\[\begin{equation} p_\textrm{RAG-Token} (y \vert x) \approx \prod_i^N \sum_{z \in \textrm{top-k}(p(\cdot \vert x))} p_\eta (z \vert x) p_\theta (y_i \vert x, z, y_{1:i-1}) \end{equation}\]RAG는 타겟 클래스를 길이가 1인 타겟 시퀀스로 간주하여 시퀀스 분류 task에 사용될 수 있으며, 이 경우 RAG-Sequence와 RAG-Token은 동등하다.
2. Retriever: DPR
Retriever \(p_\eta (z \vert x)\)는 DPR을 기반으로 한다. DPR은 bi-encoder 아키텍처를 따른다.
\[\begin{equation} p_\eta (z \vert x) \propto \exp (\mathbf{d} (z)^\top \mathbf{q} (x)) \end{equation}\]\(\mathbf{d}(z) = \textrm{BERT}_d (z)\)는 document encoder에서 생성된 dense한 표현이며, \(\mathbf{q}(x) = \textrm{BERT}_q (x)\)는 query encoder에서 생성된 query 표현이다. 두 인코더 모두 BERT-base 모델을 기반으로 한다.
가장 높은 사전 확률 $p_\eta (z \vert x)$를 갖는 $k$개의 문서 $z$인 \(\textrm{top-k} (p_\eta (\cdot \vert x))\)를 계산하는 것은 Maximum Inner Product Search (MIPS) 문제이며, 이는 대략적으로 sub-linear time 내에 풀 수 있다. DPR의 사전 학습된 bi-encoder를 사용하여 retriever를 초기화하고 문서 인덱스를 구축한다. 이 retriever는 TriviaQA 질문과 Natural Questions에 대한 답변이 포함된 문서를 검색하도록 학습되었다. 문서 인덱스를 non-parametric memory라고 한다.
3. Generator: BART
Generator $p_\theta (y_i \vert x, z, y_{1:i−1})$는 임의의 인코더-디코더를 사용하여 모델링할 수 있다. 본 논문에서는 사전 학습된 seq2seq transformer인 BART-large를 사용하였다. BART에서 생성할 때 입력 $x$와 검색된 콘텐츠 $z$는 간단히 concat되어 결합된다. BART generator의 파라미터 $\theta$를 parametric memory라고 한다.
4. Training
어떤 문서를 검색해야 하는지에 대한 직접적인 supervision 없이 retriever와 generator를 공동으로 학습시킨다. 입력/출력 쌍 $(x_j, y_j)$로 구성된 fine-tuning 데이터가 주어지면 Adam을 사용한 stochastic gradient descent을 사용하여 각 타겟의 negative marginal log-likelihood $\sum_j − \log p (y_j \vert x_j)$를 최소화한다. 학습 중에 document encoder \(\textrm{BERT}_d\)를 업데이트하는 것은 문서 인덱스를 주기적으로 업데이트해야 하므로 비용이 많이 든다. 저자들은 이 단계가 강력한 성능을 위해 필요하지 않다고 생각하고 document encoder와 문서 인덱스를 고정한 채 query encoder \(\textrm{BERT}_q\)와 BART generator만 fine-tuning한다.
5. Decoding
테스트 시에는 RAG-Sequence와 RAG-Token이 서로 다른 방법으로 $\arg \max_y p(y \vert x)$를 근사한다.
RAG-Token
RAG-Token 모델은 transition probability가 다음과 같은 표준적인 autoregressive seq2seq generator로 볼 수 있다.
\[\begin{equation} p_\theta^\prime (y_i \vert x, y_{1:i−1}) = \sum_{z \in \textrm{top-k}(p(\cdot \vert x))} p_\eta (z_i \vert x) p_\theta (y_i \vert x, z_i, y_{1:i−1}) \end{equation}\]디코딩하려면 \(p_\theta^\prime (y_i \vert x, y_{1:i−1})\)을 표준 beam search 디코더에 넣으면 된다.
RAG-Sequence
RAG-Sequence의 경우, likelihood $p(y \vert x)$는 per-token likelihood로 분리되지 않으므로 한 번의 beam search로 해결할 수 없다. 대신 각 문서 $z$에 대해 beam search를 실행하여 $p_\theta (y_i \vert x, z, y_{1:i−1})$을 사용하여 각 가설을 채점한다. 그러면 가설들의 집합 $Y$가 생성되는데, 이 중 일부는 모든 문서의 beam에 나타나지 않았을 수 있다. 가설 $y$의 확률을 추정하기 위해 beam에 $y$가 나타나지 않는 각 문서 $z$에 대해 추가 forward pass를 실행하고, generator 확률을 $p_\eta (z \vert x)$로 곱한 다음 marginal들에 대한 beam 전체의 확률을 합산한다. 이 디코딩 절차를 Thorough Decoding이라고 한다.
더 긴 출력 시퀀스의 경우 $Y$의 크기가 커져 여러 forward pass가 필요할 수 있다. 보다 효율적인 디코딩을 위해 $y$가 beam search에서 생성되지 않은 경우 $p_\theta (y \vert x, z_i) ≈ 0$로 추가 근사를 할 수 있다. 이렇게 하면 $Y$가 생성된 후 추가 forward pass를 실행할 필요가 없다. 이 디코딩 절차를 Fast Decoding이라고 한다.
Experiments
1. Open-domain Question Answering
다음은 Open-Domain QA에 대한 테스트 점수를 비교한 표이다.
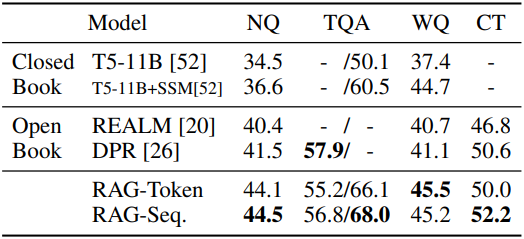
2. Generation and Classification
다음은 Jeopardy Quesion Generation, MS-MARCO (Abstractive QA), FEVER (사실 검증)에 대한 테스트 점수를 비교한 표이다.
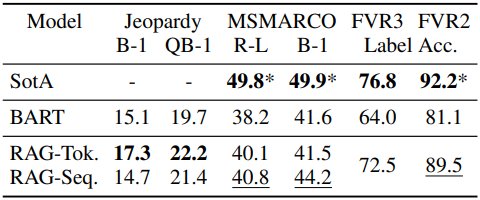
Jeopardy 문제는 종종 두 가지 별개의 정보를 담고 있으며, RAG-Token은 여러 문서의 내용을 결합한 응답을 생성할 수 있기 때문에 가장 좋은 성과를 낼 수 있다. 다음은 5개의 검색된 문서에 대하여 입력 “Hemingway”에 대해 생성된 각 토큰에 대한 RAG-Token posterior $p(z_i \vert x, y_i, y_{−i})$를 시각화한 것이다.

문서 1의 posterior는 “A Farewell to Arms”를 생성할 때 높고, 문서 2의 posterior는 “The Sun Also Rises”를 생성할 때 높다.
다음은 Jeopardy Quesion Generation과 MS-MARCO에 대한 예시이다.

다음은 Jeopardy Quesion Generation에 대한 인간 평가 결과이다.
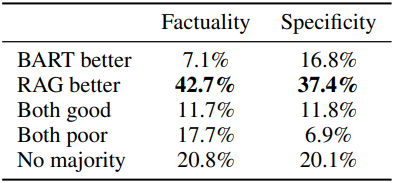
3. Additional Results
다음은 전체 tri-gram에 대한 고유 tri-gram의 비율을 비교한 표이다.
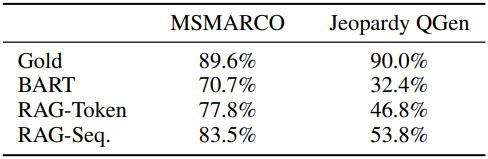
RAG-Sequence의 생성이 RAG-Token의 생성보다 더 다양하며, 둘 다 다양성을 촉진하는 디코딩이 필요 없이 BART보다 훨씬 더 다양하다는 것을 보여준다.
다음은 ablation 결과이다.
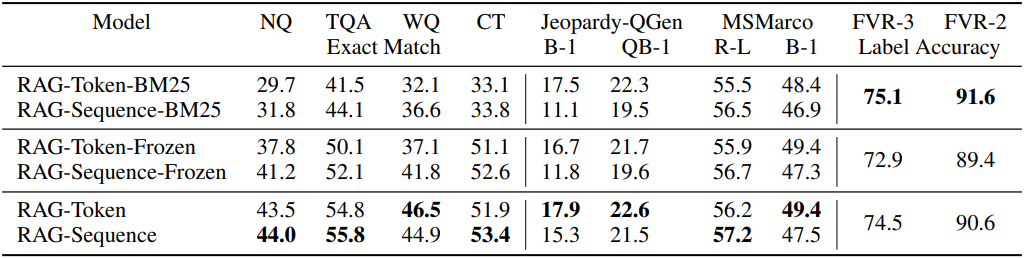
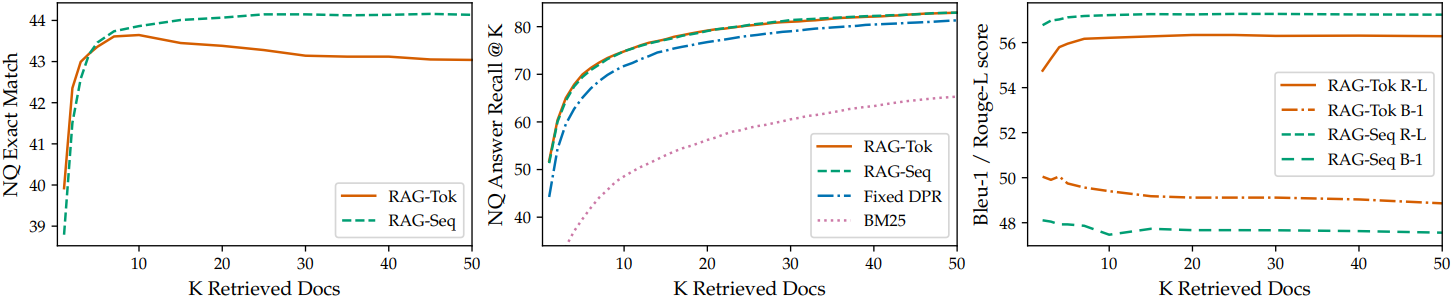
다음은 검색된 문서 수에 따른 Natural Questions (NQ) 성능을 비교한 그래프이다.