[논문리뷰] RadSplat: Radiance Field-Informed Gaussian Splatting for Robust Real-Time Rendering with 900+ FPS

3DV 2025 (Oral). [Paper] [Page]
Michael Niemeyer, Fabian Manhardt, Marie-Julie Rakotosaona, Michael Oechsle, Daniel Duckworth, Rama Gosula, Keisuke Tateno, John Bates, Dominik Kaeser, Federico Tombari
Google
20 Mar 2045

Introduction

3D Gaussian Splatting (3DGS)은 최적화 환경이 까다롭고 모델 크기가 제한적이라는 단점이 있다. Gaussian의 개수는 사전에 알려져 있지 않으며, 만족스러운 결과를 얻으려면 신중하게 조정된 병합, 분할, pruning 휴리스틱이 필요하다. 이러한 휴리스틱의 취약성은 exposure 변화, 모션 블러, 움직이는 물체와 같은 현상이 불가피한 대규모 장면에서 특히 두드러진다. Gaussian의 수가 증가함에 따라 메모리 사용량이 증가하여 렌더링 속도가 저하되고, 이는 대규모 장면의 모델 품질을 심각하게 제한한다.

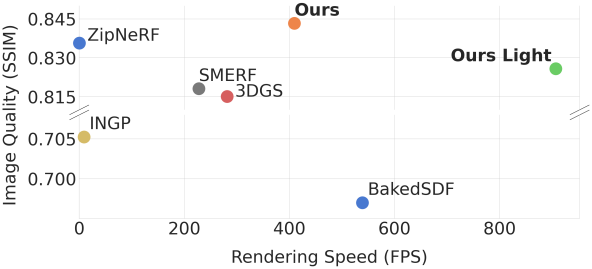
본 연구에서는 복잡한 실제 장면의 강건한 실시간 렌더링을 위한 경량 기법인 RadSplat을 제시하였다. RadSplat은 3DGS보다 더 작은 모델 크기와 더 빠른 렌더링 속도를 달성하는 동시에 재구성 품질을 크게 향상시킨다. 핵심 아이디어는 NeRF의 안정적인 최적화와 품질을 결합하여 포인트 기반 장면 표현 최적화를 위한 prior와 supervision 신호 역할을 하는 것이다. 또한, 새로운 pruning 절차와 test-time visibility 렌더링 전략을 도입하여 메모리 사용량을 크게 줄이고 품질 저하 없이 렌더링 속도를 향상시켰다.

RadSplat은 중대형 장면 모두에서 SOTA 재구성 품질을 보여주었다. PSNR은 3DGS보다 최대 1.87dB 높고, SSIM은 현재 SOTA인 Zip-NeRF를 능가한다. 동시에, 최대 FPS는 907로 3DGS보다 3.6배 이상, Zip-NeRF보다 3,000배 이상 빠르다.

Method

1. Neural Radiance Fields as a Robust Prior

실제 캡처에는 조명 및 exposure 변화나 모션 블러와 같은 효과가 포함되는 경우가 많다. 이러한 실제 환경에서 NeRF의 성공을 위해서는 NeRF in the Wild에서와 같이 Generative Latent Optimization (GLO) 임베딩 벡터를 사용하는 것이 중요하다. 더 구체적으로, 이미지별 latent 벡터는 radiance field와 함께 최적화되어 이미지 및 시점 의존적 효과를 설명할 수 있다.

\[\begin{equation} \mathcal{L}(\theta, \{\textbf{l}_i\}_{i=1}^N) = \sum_{\textbf{r}_i \in \mathcal{R}_\textrm{batch}} \| \textbf{c}_\textrm{NeRF}^{\theta, l_i} (\textbf{r}_i) - \textbf{c}_\textrm{GT} (\textbf{r}_i) \|_2^2 \end{equation}\]

(\(\{\textbf{l}_i\}_{i=1}^N\)은 GLO 벡터 집합, $N$은 입력 이미지 개수)

이를 통해 모델은 입력 이미지에서 포착된 외형 변화를 floating 아티팩트와 같은 잘못된 geometry 없이 표현할 수 있다. 테스트 시에는 이미지를 상수 latent 벡터, 일반적으로 영 벡터로 렌더링하여 안정적이고 고품질의 뷰 합성을 얻을 수 있다.

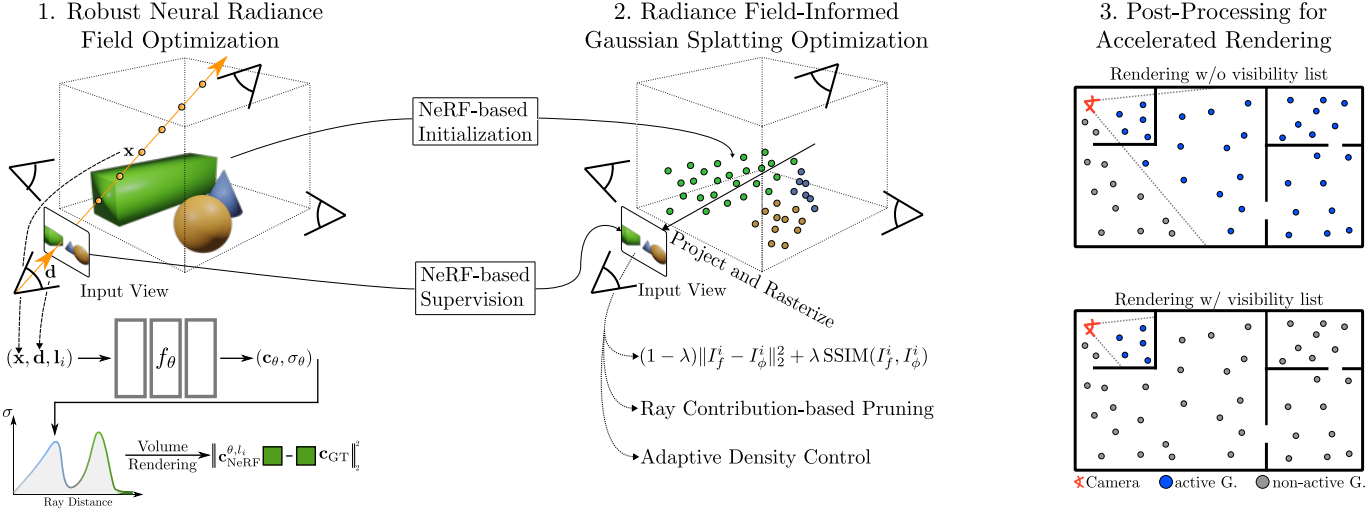
2. Radiance Field-Informed Gaussian Splatting

Radiance Field-based Initialization

Radiance field의 핵심 강점은 볼륨 렌더링 패러다임에 있다. Radiance field는 기존 표면 렌더링 기술과 달리 3D 공간에서 밀도를 자유롭게 초기화, 제거 및 변경할 수 있다. 반면, 명시적인 포인트 기반 표현은 rasterization 기반 접근 방식으로 인해 기존 geometry 예측에 대한 gradient 신호만 제공할 수 있다. 따라서 이러한 표현의 초기화는 최적화 과정에서 중요한 속성이다.

본 논문은 적절한 초기화를 위해 radiance field prior를 사용하는 것을 제안하였다. 구체적으로, 각 픽셀/광선 $\textbf{r}$에 대해 NeRF 모델의 중간 깊이 \(z_\textrm{median}\)을 누적 투과율 \(\tau_i\)가 0.5를 넘어서는 첫 샘플까지의 거리로 정의한다. 모든 픽셀/광선을 3D 공간으로 unprojection하여 초기 포인트 집합을 얻는다.

\[\begin{equation} \mathcal{P}_\textrm{init} = \{ \textbf{p}_i \}_{i \in \mathcal{K}_\textrm{ind}}, \quad \textbf{p}_i = \textbf{r}_0 (i) + \textbf{d}_{\textbf{r} (i)} \cdot z_\textrm{median} (\textbf{r}(i)) \end{equation}\]

(\(\mathcal{K}_\textrm{ind}\)는 모든 광선/픽셀 목록에 대해 무작위로 샘플링된 인덱스, \(\textbf{r}_0\)는 광선 원점, $\textbf{d}$는 정규화된 광선 방향)

중간 깊이 추정은 정확한 샘플링 지점 추정치를 사용하므로 깊이 기댓값과 같은 다른 일반적인 방법보다 성능이 더 우수하며, 모든 장면에 대해 \(\vert \mathcal{K}_\textrm{rnd} \vert\)를 100만으로 설정하면 잘 작동한다.

Spherical harmonics (SH) 계수 \(\textbf{k}_i \in \mathbb{R}^{48}\)와 3D scale \(\textbf{s}_i \in \mathbb{R}^3\)은 다음과 같이 초기화한다.

\[\begin{aligned} \textbf{k}_i &= (\textbf{k}_i^{1:3}, \textbf{k}_i^{4:48}), \quad \textbf{k}_i^{1:3} = \textbf{c}_\textrm{NeRF}(\textbf{r}(i)), \; \textbf{k}_i^{4:48} = \textbf{0} \\ \textbf{s}_i &= (s_i, s_i, s_i), \quad s_i = \min_{\textbf{p} \in \{\textbf{p} = \textbf{p}_i \vert \textbf{p} \in \mathcal{P}_\textrm{init}\}} \| \textbf{p}_i - \textbf{p} \|_2 \end{aligned}\]

불투명도 $o_i \in [0,1]$은 0.1로, rotation quaternion \(\textbf{q}_i\)는 identity rotation으로 설정된다. 따라서 각 장면에 대해 다음을 최적화한다.

\[\begin{equation} \phi = \{ (\textbf{p}_i, \textbf{k}_i, \textbf{s}_i, o_i, \textbf{q}_i) \}_{i=1}^{N_\textrm{init}} \end{equation}\]

Radiance Field-based Supervision

실제 환경에서 촬영된 이미지에 exposure 및 조명 변화가 까다로운 경우에도 radiance field가 탁월한 성능을 보이는 것으로 나타났다. 이러한 radiance field의 강점을 활용하여 데이터의 복잡성과 노이즈를 제거하여 손상되었을 가능성이 있는 입력 이미지보다 더 정제된 supervision 신호를 제공한다.

구체적으로, 모든 입력 이미지를 NeRF 모델 \(f_\theta\)와 0으로 설정된 GLO 벡터 \(\textbf{l}_\textrm{zero}\)를 사용하여 렌더링한다.

\[\begin{equation} \mathcal{I}_f = \{ I_f^j \}_{j=1}^N \quad \textrm{where} \quad I_f^j = \{ \textbf{c}_\textrm{NeRF}^{\theta, l_\textrm{zero}} (\textbf{r}_j (i)) \}_{i=1}^{H \times W} \end{equation}\]

이러한 렌더링을 사용하여 포인트 기반 표현을 학습할 수 있다.

\[\begin{equation} \mathcal{L}(\phi) = (1 - \lambda) \| I_f^i - I_\phi^i \|_2^2 + \lambda \textrm{SSIM} (I_f^i, I_\phi^i) \end{equation}\]

($i \sim \mathcal{U}$, $\lambda = 0.2$)

또 다른 실질적인 이점은 NeRF의 유연한 ray casting 덕분에 임의의 카메라 렌즈 유형을 학습할 수 있다는 것이다. 반면, 3DGS는 핀홀 카메라 모델을 가정하며, 이를 fisheye 렌즈나 더 복잡한 렌즈 유형으로 효율적으로 확장하는 방법은 불분명하다.

3. Ray Contribution-Based Pruning

3DGS 표현은 rasterization 덕분에 효율적으로 렌더링할 수 있지만, 실시간 성능을 위해서는 여전히 강력한 GPU가 필요하다. 렌더링 성능에서 가장 중요한 요소는 장면에서 렌더링해야 하는 포인트의 수이다.

Importance Score

저자들은 더 빠르게 렌더링할 수 있는 더 가벼운 표현을 얻기 위해, 장면에서 Gaussian의 개수를 줄이면서도 높은 품질을 유지하는 새로운 pruning 기법을 개발했다. 더 구체적으로, 최적화 과정에서 학습 뷰에 크게 기여하지 않는 점들을 제거하는 pruning 단계를 도입했다. 이를 위해 모든 입력 이미지의 모든 광선에 대해 Gaussian \(\textbf{p}_i\)의 광선 기여도를 집계하여 중요도 점수를 정의했다.

\[\begin{equation} h (\textbf{p}_i) = \max_{I_f \in \mathcal{I}_f, r \in I_f} \alpha_i^r \tau_i^r \end{equation}\]

(\(\alpha_i^r \tau_i^r\)은 광선 $\textbf{r}$에 대한 Gaussian \(\textbf{p}_i\)의 기여도)

이 공식은 불투명도가 아닌 정확한 광선 기여도와 평균이 아닌 최댓값을 사용하기 때문에 비슷한 방법들보다 결과가 향상되었다. max 연산자는 입력 이미지 수에 독립적이므로 다양한 유형의 장면 적용 범위에 더 강하다.

Pruning

최적화 과정에서 중요도 점수를 사용하여 장면의 전체 포인트 수를 줄이는 동시에 높은 품질을 유지한다. 더 구체적으로, 마스크 값을 다음과 같이 계산하는 pruning 단계를 추가한다.

\[\begin{equation} m_i = m (\textbf{p}_i) = \unicode{x1D7D9} (h (\textbf{p}_i) < t_\textrm{prune}), \quad t_\textrm{prune} \in [0, 1] \end{equation}\]

장면에서 마스크 값이 1인 모든 Gaussian을 제거한다. 최적화 과정 전체에 걸쳐 pruning 단계를 두 번 적용한다 (16k, 24k). Threshold \(t_\textrm{prune}\)은 장면을 표현하는 데 사용되는 포인트의 개수를 제어하는 ​​메커니즘을 제공하며, 기본 모델은 0.01, 경량 모델은 0.25를 사용한다.

4. Viewpoint-Based Visibility Filtering

본 논문의 pruning 기법은 전체 포인트 수가 적은 간결한 장면 표현을 보장한다. 고전적인 occlusion culling에서 영감을 받아, 크고 복잡한 장면으로 확장하기 위해, 새로운 시점 기반 필터링을 후처리 단계로 도입하여 품질 저하 없이 test-time 렌더링 속도를 더욱 향상시킨다.

Input Camera Clustering

먼저, 장면 공간의 의미 있는 테셀레이션을 얻기 위해 입력 카메라를 그룹화한다. 구체적으로, 입력 이미지 집합 $\mathcal{I}$에 대한 입력 카메라 위치에 대해 kmeans clustering을 실행하여 k개의 클러스터 중심 \((\textbf{x}_\textrm{cluster}^i)_{i=1}^k\)를 얻고, 입력 카메라를 각 클러스터 중심에 할당한다 (실험에서는 $k = 64$ 사용).

Visibility Filtering

다음으로, 각 클러스터 중심 \(\textbf{x}_\textrm{cluster}^j\)에 대해 할당된 모든 입력 카메라를 선택하고 이러한 시점에서 이미지를 렌더링하고 중요도 점수와 visibility indicator list를 계산한다.

\[\begin{aligned} h_j^\textrm{cluster} (\textbf{p}_i) &= \max_{I \in \mathcal{I}_c^i, r \in I} \alpha_i^r \tau_i^r \\ m_j^\textrm{cluster} (\textbf{p}_i) &= \unicode{x1D7D9} (h_j^\textrm{cluster} (\textbf{p}_i) > t_\textrm{cluster}) \end{aligned}\]

(\(\mathcal{I}_c^i\)는 클러스터 중심 \(\textbf{x}_\textrm{cluster}^i\)에 할당된 이미지 집합, \(t_\textrm{cluster} = 0.001\)은 필터링되어야 하는 포인트의 기여도 값을 제어하는 threshold)

실제로는 테스트 뷰에 대한 robustnes를 보장하기 위해 \(\mathcal{I}_c^i\)에 무작위 카메라 샘플을 추가한다. 장면 최적화 후 후처리 단계로 각 클러스터 중심의 indicator list \(m_j^\textrm{cluster}\)를 계산한다.

Visibility List-Based Rendering

임의의 시점을 렌더링하기 위해 먼저 카메라 중심 $\textbf{x}$를 가장 가까운 클러스터 중심 \(\textbf{x}_\textrm{cluster}^i\)에 할당한다. 다음으로, 해당 indicator list \(m_j^\textrm{cluster}\)를 선택하고, 활성으로 표시된 포인트만 고려하여 rasterization을 수행한다. 이를 통해 품질 저하 없이 최대 45%까지 FPS가 크게 향상된다.

Experiments

• 데이터셋: MipNeRF360, Zip-NeRF

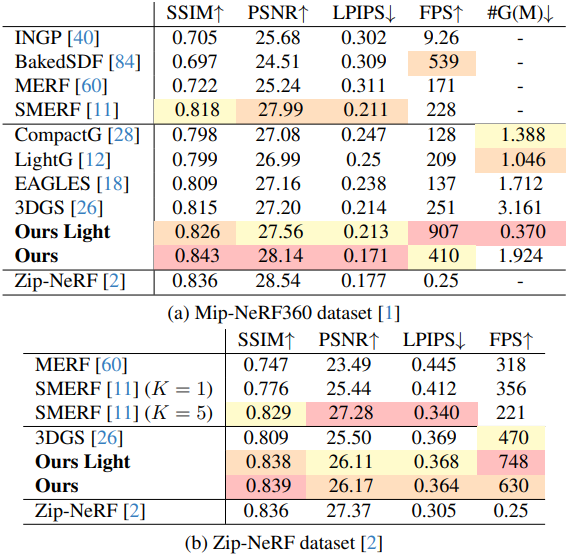
1. Real-Time View Synthesis

다음은

2. Ablation Study

다음은 ablation study 결과이다.

다음은 pruning threshold에 따른 성능을 비교한 결과이다.

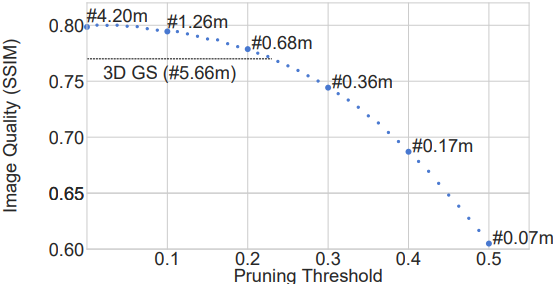
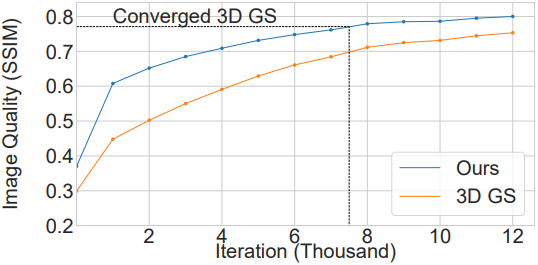
다음은 학습 과정에서의 렌더링 품질을 3DGS와 비교한 결과이다.

다음은 visibility filtering에 대한 ablation 결과이다.