[논문리뷰] Radiant Foam: Real-Time Differentiable Ray Tracing
ICCV 2025. [Paper] [Page] [Github]
Shrisudhan Govindarajan, Daniel Rebain, Kwang Moo Yi, Andrea Tagliasacchi
Fudan University | ByteDance
3 Feb 2025

Introduction
NeRF는 2D 이미지 컬렉션에서 dense한 3D 표현을 추출할 수 있게 함으로써 3D 컴퓨터 비전에 혁명을 일으켰다. 초기 NeRF는 느린 렌더링 속도에 문제가 있었지만, 그 이후로 보다 효율적인 모델과 고효율 렌더링을 가능하게 하는 모델을 distillation하는 기술을 개발되었다. 특히, 실시간 렌더링 성능은 GPU 하드웨어에서 쉽게 사용할 수 있는 rasterization 파이프라인을 활용하여 가능해졌다. 그 후 rasterization을 학습 프로세스에 통합할 것이 제안되었고, 그 결과 3D Gaussian Splatting (3DGS)이 개발되었다.
최근 3DGS에 대한 연구가 활발히 진행되고 있으며, 많은 연구가 rasterization으로 인해 발생하는 문제를 해결하려는 듯 보인다. 또한, 일부 연구에서는 3DGS와 ray tracing을 통합하여 렌더링 속도를 높이고 보다 복잡한 빛의 상호작용을 구현하기도 했다. 하지만 연구자들은 여전히 새로운 3D 표현 방식을 탐구하고 있다. 특히, 컴퓨터 그래픽스 분야에서 오랜 기간 핵심 역할을 해온 다각형 메쉬(polygonal mesh)에 대한 관심이 다시금 커지고 있다. 일부 연구에서는 메쉬를 활용하여 radiance field를 모델링하려는 흥미로운 시도를 보여주었다. 그러나 현실적으로 이러한 접근 방식이 3DGS를 대체할 만큼 강력한 radiance field 학습 표현으로 자리 잡지는 못했다.
Hardware-based view-independent cell projection 논문에서는 메쉬로 표현된 필드가 특수 하드웨어가 필요 없는 매우 효율적인 ray tracing 알고리즘을 가능하게 한다는 것을 보여주었다. 본 논문에서는 이 표현을 미분 가능하게 만들고 기본 메쉬에 대한 정제 기술을 신중하게 설계하였다. 이러한 정제를 통해 물체 표면을 정확하게 표현하면서도 빈 부분을 건너뛰어 효율적으로 렌더링할 수 있다.
본 논문의 방법인 Radiant Foam은 3DGS와 유사한 렌더링 속도와 품질을 제공하지만 NeRF와 유사한 광선 기반 학습 방식을 가지고 있다. 즉, 많은 NeRF 기술을 Radiant Foam에 완벽하게 적용할 수 있으며, 기본 형상이 메쉬로 명시적으로 표현된다는 상당한 이점이 있다. 저자들은 이 메쉬를 3D Voronoi diagram으로 parameterize하여 불연속성을 피함으로써 gradient descent를 통해 동적인 connectivity를 가진 메쉬 구조를 학습할 수 있다. 또한 적응형 해상도로 메쉬 모델을 빠르게 구성할 수 있는 coarse-to-fine 학습 방식을 제안하였다.
Method
1. Volume rendering
볼륨 렌더링은 현대의 미분 가능한 장면 재구성 방법의 주력이 되었다. 볼륨 렌더링을 사용하면 공간의 모든 지점이 해당 지점을 통과하는 광선의 색상에 지속적으로 다양한 기여를 할 수 있다. 이 기여의 효과는 occlusion을 생성하는 density field와 관찰되는 빛의 밝기를 결정하는 radiance field에 의해 제어된다. 연속적인 필드의 볼륨 렌더링은 시점과 density field, radiance field 값을 포함하여 모든 자유도에 대해 완전히 연속적이다. 이 속성은 gradient 기반 최적화에 매우 적합하다.
볼륨 렌더링은 관찰 광선의 세그먼트 \((t_\textrm{min}, t_\textrm{max})\)에 대한 적분으로 정의된다. 구체적으로 광선 $\textbf{r}$에 대한 관찰 색상 \(\textbf{c}_\textbf{r}\)은 다음과 같다.
\[\begin{aligned} \textbf{c}_\textbf{r} &= \int_{t_\textrm{min}}^{t_\textrm{max}} T(t) \cdot \sigma (\textbf{r} (t)) \cdot \textbf{c} (\textbf{r}(t)) dt \\ T(t) &= \exp \left( - \int_{t_\textrm{min}}^t \sigma (\textbf{r} (u)) du \right) \end{aligned}\]($\textbf{r}(t)$는 광선 $\textbf{r}$을 따라 거리 $t$에 있는 3D 공간의 점, $\sigma(\cdot)$는 density field, $\textbf{c}(\cdot)$는 radiance field)
Piecewise constant volumes
$\sigma (\cdot)$와 $\textbf{c} (\cdot)$가 piecewise-constant인 경우, 적분은 모든 $N$개 광선 세그먼트에 대한 합으로 표현될 수 있다.
\[\begin{aligned} \textbf{c}_\textbf{r} &= \sum_{n=1}^N T_n \cdot (1 - \exp (- \sigma_n \delta_n)) \cdot \textbf{c}_n dt \\ T(t) &= \prod_{j=1}^n \exp (- \sigma_j \delta_j) \end{aligned}\](\(\delta_n\)은 세그먼트 $n$의 길이)
이 공식은 깊이 순서대로 세그먼트를 반복하는 간단한 구현을 가능하게 한다. NeRF는 적분 형태의 볼륨 렌더링의 근사치로 위 식을 사용하며, 세그먼트는 중요도 샘플링 방식에 따라 샘플링된다.
반대로, Radiant Foam에서 이러한 형태는 정확히 동등하다. 저자들은 Hardware-based view-independent cell projection의 알고리즘을 활용하고, 메쉬 셀 내에서 field 값을 일정하게 유지하는 모델을 적용하여 위 식이 정확한 볼륨 렌더링 결과를 제공할 것을 제안하였다.
이 선택은 복잡하거나 값비싼 샘플링 방식을 피하는 데 매우 유리하지만 gradient 기반 최적화에 중요한 표현의 연속성을 방해하지 않도록 주의해야 한다. 특히, 메쉬 자체는 셀 경계와 광선의 교차점 위치에 의해 결정되는 세그먼트 길이 \(\delta_n\)을 통해서만 gradient를 받는다. 따라서 이러한 경계 교차점은 모델의 최적화 가능한 파라미터에 따라 지속적으로 변하는 것이 중요하다.
2. Differentiable mesh representation
일반적으로 메쉬는 두 그룹의 자유도, vertex 위치 $\mathcal{V}$와 셀 $\mathcal{C}$ (즉, connectivity)에 따라 결정된다. 다른 모든 파라미터가 고정되어 있다고 가정하면 vertex 위치에 대한 최적화는 일반적으로 간단하다. 광선과 셀 경계의 교차점은 vertex 위치에 따라 부드럽게 달라지기 때문이다. 표현의 connectivity $\mathcal{C}$도 최적화하려는 경우 진정한 문제가 발생한다.
The Delaunay triangulation
메쉬의 connectivity는 본질적으로 불연속적이기 때문에 gradient 기반 방법으로 직접 최적화할 수 없다. 이 문제를 피하기 위해 vertex 위치에 따라 connectivity를 정의하여 각 vertex 구성이 고유한 셀 집합에 해당하도록 할 수 있다. 이 매핑에 가장 명확한 선택은 Delaunay triangulation으로, 3D에서 4개의 vertex로 형성될 수 있는 모든 사면체 셀 \(\textbf{c}_i \in \mathcal{C}\)의 집합으로 구성되며, 해당 외접구에 다른 vertex가 포함되지 않는다. Delaunay triangulation은 일반적인 점 집합에 대해 고유하며, 잘 알려지고 효율적인 알고리즘을 사용하여 쉽게 계산할 수 있다.
Delaunay triangulation을 미분 가능한 볼륨 렌더링의 기초로 사용하려는 경우 두 가지 중요한 문제에 부딪힌다.
- Delaunay 셀의 경계가 vertex가 다른 셀의 외접구에 들어갈 때마다 불연속적인 “flip”을 겪기 때문에 메쉬 connectivity의 불연속적 특성을 완전히 피할 수 없다. 이러한 flip은 최적화에 불연속성을 도입하여 gradient descent의 수렴을 방해한다.
- 이 모델에서 사면체의 수는 고정되어 있지 않으므로 각 셀을 최적화 가능한 $\sigma$와 $\textbf{c}$ 값과 연관시키는 것이 간단하지 않다. Field의 값을 vertex와 연관시키고 셀 내에서 해당 값을 보간하여 해결할 수 있지만 볼륨 렌더링이 복잡해진다.
The Voronoi diagram
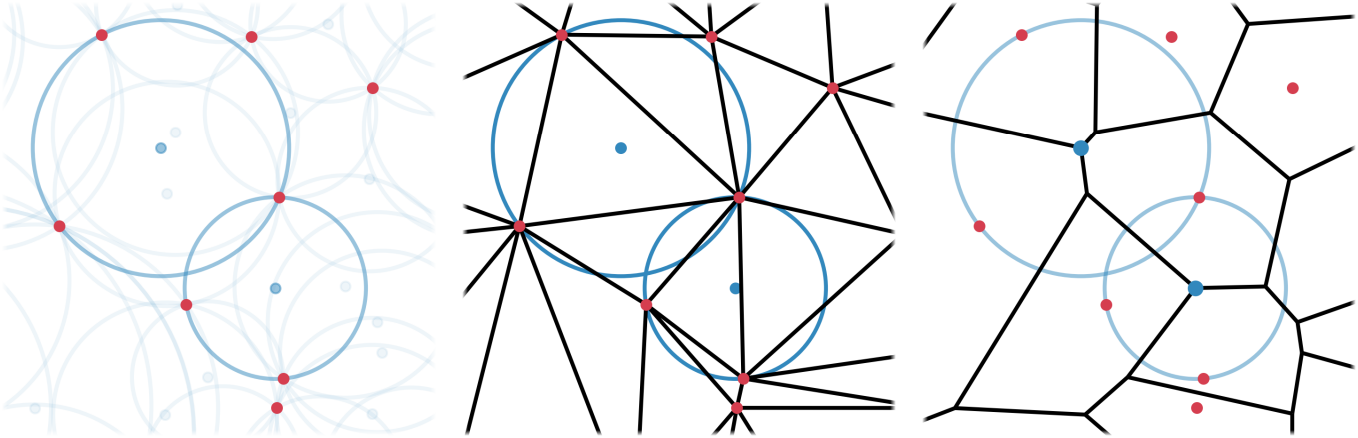
Delaunay 메쉬를 직접 사용하여 한계를 극복하기보다는 Delaunay triangulation과 duality에 있는 Voronoi diagram을 살펴보자. Voronoi diagram은 각 Delaunay 사면체의 외심에 vertex를 두어 구성된다. 공간을 볼록 다면체 셀 \(\textbf{c}_i \in \mathcal{C}\)로 분할하는데, 이 셀은 Delaunay triangulation의 vertex \(\textbf{p}_i\)가 nearest neighbor인 점들로 구성된다.
Delaunay triangulation이 최적화에서 불연속적이라면, 그 duality인 Voronoi diagram도 같은 문제를 겪지 않을까? 이 질문에 대한 답은 Voronoi diagram의 connectivity에 대한 모든 불연속적 변화가 영향을 받는 셀 면이 표면적이 0이 되는 지점과 정확히 일치한다는 사실에 있다.
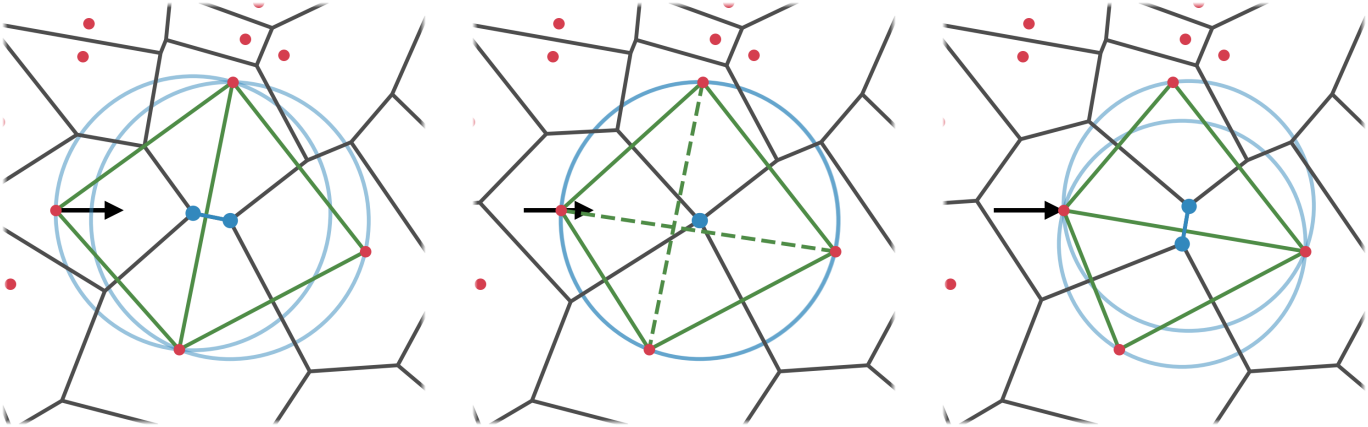
위 그림에서 초록색 선들이 Delaunay graph의 connectivity이며, vertex가 업데이트됨에 따라 connectivity가 불연속적으로 바뀌는 것을 볼 수 있다.
반면, Voronoi diagram의 경우 불연속적인 flip은 부피가 0인 영역 내에 효과적으로 숨겨지고 (파란색 선), field 표현은 vertex 위치에 대해 완전히 연속적으로 유지된다. Voronoi diagram의 셀 개수는 구성과 관계없이 일정하기 때문에, $\sigma$와 $\textbf{c}$ 값을 셀에 할당하는 과정이 단순해진다. 결과적으로, 이 모델은 학습 가능한 포인트 클라우드와 유사하게 작동하며, 3DGS의 개념과 크게 다르지 않지만, 각 포인트별 공분산 행렬이 존재하지 않는다는 차이가 있다.
Ray tracing
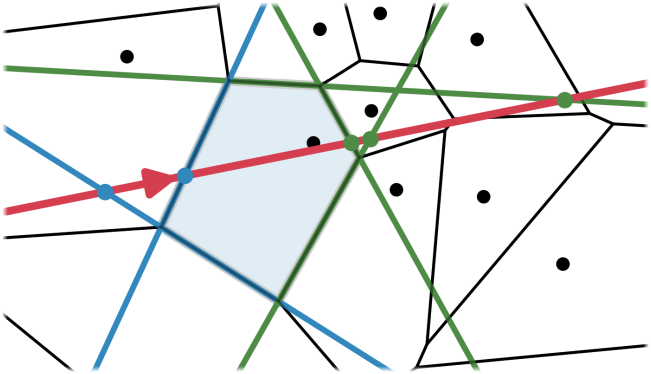
한 가지 남은 문제는 ray tracing 알고리즘이 기본적으로 사면체 셀을 가정한다는 점이다. 따라서 저자들은 알고리즘을 보다 일반적인 볼록(convex) 셀을 처리할 수 있도록 수정하였다.
Volume rendering을 하기 위해서는 광선을 따라 누적되는 셀들의 순서를 알아야 하며, 각 셀에 대한 세그먼트의 길이 \(\delta_n\)을 계산해야 한다. 즉, 어떤 셀로 광선이 들어갔을 때, 어디로 나가는 지를 계산해야 한다.
이를 위해, 현재 셀의 vertex와 인접한 vertex들에 대하여 각각 수직 이등분면을 계산하고, 각 수직 이등분면과 광선 사이의 교차점을 계산한다. 그러면, 수직 이등분면의 normal과 광선 방향 사이의 각도가 90°보다 작은 면 (위 그림에서 초록색 선) 중에서 교차점이 가장 가까운 점이 광선이 나가는 점이다. 자연스럽게 다음 셀이 특정되기 때문에 이 과정을 반복해서 다음 셀을 찾고 세그먼트의 길이 \(\delta_n\)을 계산할 수 있다.
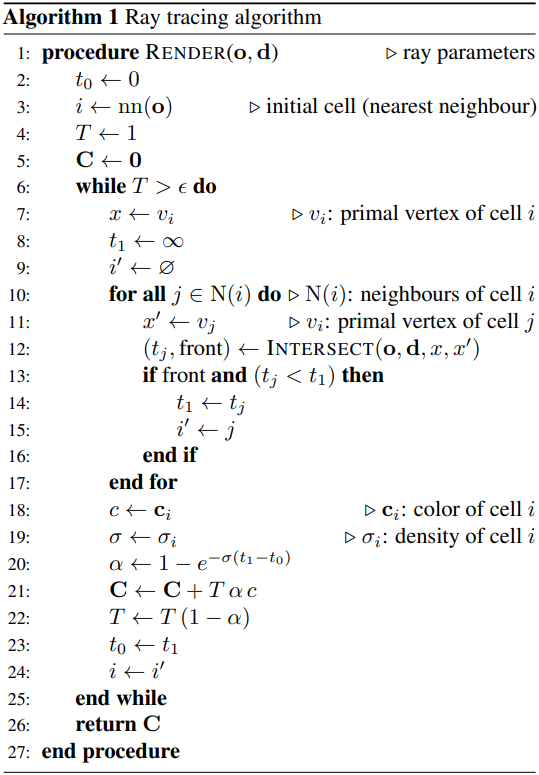
3. Optimization
3DGS와 유사하게, Voronoi 셀의 로컬한 특성은 최적화를 local minima에 더 취약하게 만든다. 우리는 유사한 전략을 따르는데, 먼저 최적화를 신중하게 초기화한 다음 Voronoi site를 적응적으로 densify하고 pruning한다. 또한 표면과 같은 밀도의 형성을 촉진하기 위해 NeRF에서 일반적으로 사용하는 distortion loss와 유사한 정규화 loss도 사용한다.
(Voronoi site: Voronoi diagram에서 셀을 나누는 기준이 되는 점)
Densification
3DGS와 유사하게, 학습을 초기화하기 위해 COLMAP에서 얻은 sparse한 포인트 클라우드로 시작한다. 학습을 통해 Voronoi site의 수와 density를 제어하기 위해 densification과 pruning 연산을 수행하여 모델이 더 디테일한 공간 영역에 표현 용량을 적응적으로 재할당할 수 있도록 한다.
Voronoi site 위치에 대한 reconstruction loss의 gradient를 사용하여 학습 신호에 underfitting한 셀을 식별할 수 있다. 따라서 이 gradient의 norm에 셀의 대략적인 반경을 곱하여 densification이 필요한 셀을 측정한다. 이 측정값에 비례하는 확률 질량 함수를 갖는 다항 분포를 샘플링하여 densification 후보를 선택한다.
Pruning
간결한 표현을 구축하기 위해 렌더링에 기여하지 않는 Voronoi diagram에서 셀을 제거한다. 그러나 단순히 빈 셀, 즉 density가 0인 셀을 삭제하는 것만으로는 충분하지 않다. Voronoi 셀의 형상은 해당 셀의 density가 0인 경우에도 인접한 사이트의 위치에 따라 결정되기 때문이다. 따라서 물체 경계를 정확하게 표현하려면 경계를 정의하는 density가 거의 0에 가까운 셀을 유지하는 것이 필수적이다.
이러한 이유로, 본 논문의 pruning 전략은 density가 매우 낮고 매우 낮은 density의 이웃으로 둘러싸인 Voronoi site를 제거한다. 이 pruning은 표면에 기여하지도 정의하지도 않는 Voronoi site를 제거하여 물체 경계의 정확성을 유지한다.
Training objectives
Mip-NeRF 360의 distortion loss와 유사하게, 광선을 따라 볼륨 렌더링 적분에 대한 기여 분포에 정규화를 적용한다. 이 추가 loss function은 density가 표면에 집중되도록 장려하고 눈에 보이는 floater 아티팩트를 줄인다. 이 loss는 다음과 같이 계산된다.
\[\begin{equation} \mathcal{L}_\textrm{quantile} = \mathbb{E}_{t_1, t_2 \sim \mathcal{U}[0, 1]} [\vert W^{-1} (t_1) - W^{-1} (t_2) \vert] \end{equation}\]($W^{-1} (\cdot)$는 광선의 볼륨 렌더링 가중치 분포의 quantile function (inverse CDF))
이 형태는 distortion loss와 동일한 효과가 있지만, 학습의 계산 비용과 메모리 사용량을 증가시키는 이중 합의 필요성을 피한다. 일반적인 L2 photometric reconstruction loss를 \(\mathcal{L}_\textrm{rgb}\)라 하면, 전반적인 loss는 다음과 같다.
\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{rgb} + \mathcal{L}_\textrm{quantile} \end{equation}\]Voronoi optimization
학습하는 동안 Voronoi 셀을 정의하는 데이터 구조를 유지한다. Vertex의 위치가 변경될 때마다 incremental Delaunay triangulation을 수행하여 adjacency를 업데이트해야 한다. 전체 구조를 모두 재구축하는 것보다는 훨씬 빠르지만, 많은 수의 vertex들에 대해서는 여전히 계산 비용이 많이 든다.
따라서 메쉬 재구축 사이에 optimizer가 여러 step을 수행할 수 있도록 한다. Densification 이후 초기에는 1:1 비율로 시작하고, 최적화가 수렴하면서 메쉬의 불연속적인 변화 빈도가 감소함에 따라 1:100까지 증가시킨다. 이러한 전략은 학습 속도와 상대적으로 정확한 메쉬 구조 유지를 균형 있게 조절하는 역할을 한다.
Experiments
- 3DGS와 마찬자기로 COLMAP의 sparse point cloud로 초기화
- 전용 ray tracing 하드웨어나 OptiX를 의존하지 않는 커스텀 CUDA 커널을 만들어 사용
- 학습 디테일
- 포인트별 위치, density, 색상 (degree 3의 SH 사용)을 최적화
- density가 $[0, \infty)$ 내에 있도록 $\beta = 10$인 softplus activation을 사용
- optimizer: Adam
- iteration: 20,000
- learning rate (cosine annealing 적용)
- 위치: $2 \times 10^{-4} \rightarrow 2 \times 10^{-6}$
- density: $1 \times 10^{-1} \rightarrow 1 \times 10^{-2}$
- SH: $5 \times 10^{-3} \rightarrow 5 \times 10^{-4}$
- 처음 5,000 iteration은 degree가 0인 SH 계수만 최적화 (warm-up)
- warm-up 후 10,000 iteration까지 densification 적용
- 마지막 2,000 iteration은 위치를 고정하고 density와 색상만 업데이트
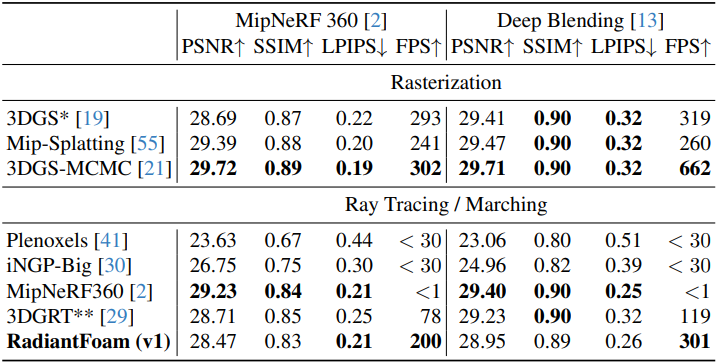
1. Quantitative results
다음은 novel view synthesis 성능을 비교한 표이다. FPS는 RTX 4090로 측정되었으며, 3DGRT만 RTX 6000 Ada로 측정되었다.
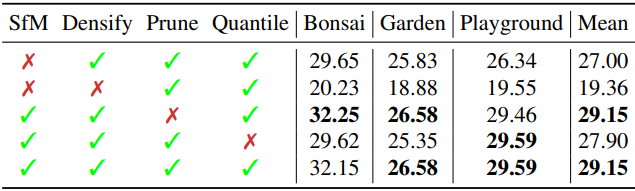
2. Ablation
다음은 ablation 결과이다.