[논문리뷰] Radiance Surfaces: Optimizing Surface Representations with a 5D Radiance Field Loss

3DV 2025 (Oral). [Paper] [Page] [Github]
Ziyi Zhang, Nicolas Roussel, Thomas Müller, Tizian Zeltner, Merlin Nimier-David, Fabrice Rousselle, Wenzel Jakob
EPFL | NVIDIA
20 Jan 2025

Introduction

표면 표현의 매력은 물체의 물리적 현실과 자연스럽게 일치한다는 점 외에도 편집, 애니메이션, 효율적인 렌더링에 적합하다는 점에 있다. 그러나 미분 가능하게 렌더링된 표면의 최적화 영역은 볼록하지 않고 local minima로 가득 차 있는 경향이 있다. 결과적으로, 현재 방법들은 복잡한 현실 세계의 장면을 처리하기에는 너무 취약한 경우가 많다.

이 문제는 volumetric 공식으로 전환함으로써 교묘하게 회피할 수 있다. Continuous한 volumetric 표현의 미분값은 평가하기 쉬울 뿐만 아니라, 더욱 매끄러운 loss 분포를 제공하여 robustness와 scalability를 향상시킨다. 그러나 이러한 개선은 추가적인 휴리스틱을 필요로 하는 더욱 복잡한 표면 추출 프로세스라는 단점이 있다.

본 논문에서는 volumetric 기법의 robustness와 수렴 속도를 유지하면서 표면을 최적화하는 간단하고 직접적인 접근법을 모색하였다. 제안하는 방법은 표면 분포를 최적화하는 간단하면서도 강력한 아이디어를 기반으로 한다. 구체적으로, 학습 사진을 장면에 projection하여 최종 light field와 표면 분포에서 발생하는 emission 사이의 차이를 최소화하는 것을 제안하였다.

결과적으로 발생하는 radiance field loss는 광선을 따라 있는 각 점을 표면 후보로 간주하고, 해당 광선의 픽셀 색상과 일치하도록 개별적으로 최적화하여 표면에 원하는 분포를 생성한다. 한 가지 이점은 광선을 따라 있는 점들이 독립적인 gradient를 받아 색상이나 밀도가 한 점에서는 증가하고 다른 점에서는 감소할 수 있다는 것이다. 이는 loss 계산 전에 광선을 따라 색상을 통합하는 volumetric 접근법과 현저히 다르다. 즉, volumetric 재구성을 사용하면 광선을 따라 있는 모든 점의 통합 색상이 너무 어둡거나 밝으면 동일한 부호의 gradient를 받아 상관 관계가 있는 조정이 이루어진다.

제안된 radiance field loss는 volumetric 재구성 방법과 매우 유사한 방정식을 도출한다. 실질적으로 이는 본 논문의 방법이 기존 volumetric 프레임워크에 쉽게 통합될 수 있음을 의미한다. 또한, 표면을 추출하기 위해 추가적인 휴리스틱을 사용하지 않고도 기존 연구의 많은 장점을 그대로 활용할 수 있음을 의미한다. Volumetric 기반 방식보다 평균 0.1dB 낮은 PSNR을 생성하면서도 거의 동일한 속도로 실행된다.

Method

1. Non-local surface perturbation

렌더링을 기하학적 구조에 따라 미분하면 작은 기하학적 섭동(perturbation)이 결과 이미지에 어떤 영향을 미치는지 알 수 있다. 그러나 이러한 미분값은 표면 자체에서만 0이 아니기 때문에 최적화에 사용될 때 수렴 문제가 발생하는 경향이 있다.

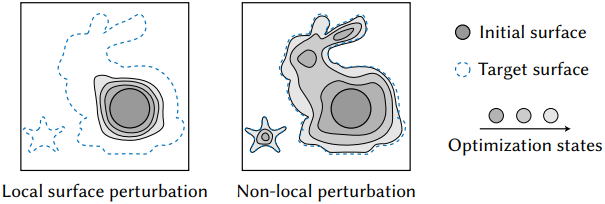
이러한 한계를 극복하기 위해, 기존 표면보다 어느 정도 떨어진 곳에 작은 표면 패치를 도입하는 효과를 고려해 보자. 이러한 수정은 렌더링된 이미지에도 영향을 미치며, 더 일반적인 non-local perturbation으로 해석될 수 있다.

이 확장된 도메인에서 표면을 최적화하면 이전에 논의된 두 가지 주요 문제가 완화된다. 업데이트가 더 이상 표면에 제한되지 않기 때문에 알고리즘은 고차원의 loss landscape에서 더 빠르고 강력한 수렴을 달성할 수 있다.

또한, 경계에서의 미분값을 추정하기 위한 복잡하고 전문적인 방법의 필요성이 제거되어 구현이 간소화되고 성능이 더욱 향상된다.

기하학적 표현

Non-local perturbation은 전체 공간을 포괄하는 표현을 필요로 한다. 이를 위해 위치 $\textbf{x}$가 점유될 discrete한 확률을 인코딩하는 occupancy field를 사용한다.

\[\begin{equation} \alpha (\textbf{x}) = \textrm{Pr} \{\textbf{x} \, \textrm{lies within an object}\} \in [0, 1] \end{equation}\]

수렴 후, 필드는 표면에서는 1에 가까운 occupancy 값을, 외부에서는 0에 가까운 occupancy 값을 가질 것으로 예상된다.

2. Radiance field loss

하나의 표면 후보

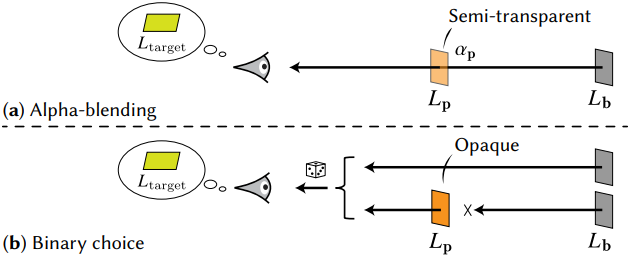
Non-local perturbation의 개념을 설명하기 위해 먼저 광선을 따라 하나의 후보 표면 패치가 존재하는 경우를 살펴보자. 위 그림은 이러한 셋업을 보여준다다. 여기서 색상이 \(L_\textbf{p}\)이고 occupancy가 \(\alpha_\textbf{p}\)인 위치 $\textbf{p}$의 후보 패치가 색상이 \(L_\textbf{b}\)인 배경보다 앞에 있다. \(L_\textbf{p}\)가 주어졌고 색상 값 \(L_\textbf{p}\)와 \(L_\textbf{b}\)는 고정되어 있다고 가정한다.

이 경우, 최적의 재구성은 간단하다. 타겟 색상 \(L_\textrm{target}\)과 관련하여 일치도가 향상되면 후보를 생성해야 하고, 그렇지 않으면 후보를 삭제해야 한다.

\(\alpha_\textbf{p}\)는 이러한 결과를 달성하는 수단을 제공한다. 그러나 이를 통합하는 방법은 여러 가지가 있다. 표준 volumetric 접근법은 \(\alpha_\textbf{p}\)를 알파 합성을 위한 불투명도로 해석하여 다음과 같은 색상 차이 $\ell (\hat{L}, L)$를 최소화한다.

\[\begin{equation} \ell (\alpha_\textbf{p} L_\textbf{p} + (1 - \alpha_\textbf{p}) L_\textbf{p}, L_\textrm{target}) \end{equation}\]

이 접근법의 근본적인 한계는 binary한 occupancy 값을 유도할 수 없다는 것이다. 최적 매칭이 \(L_\textbf{p}\)와 \(L_\textbf{b}\)의 혼합으로 주어지면, loss는 뚜렷한 표면을 형성하지 못하고 0에 도달한다. 일반적인 해결책은 이러한 동작에 페널티를 주기 위해 추가적인 loss 항을 추가하는 것이지만, 이는 원칙적인 이론적 기반이 부족하고 hyperparamter 형태로 복잡성을 가중시킨다.

대신 non-local perturbation을 이진 선택으로 해석한다. 즉, 후보 표면은 존재하거나 존재하지 않는다. 따라서 광선과 연관된 최종 색상 값은 후보 표면 \(L_\textbf{p}\) 또는 배경 표면 \(L_\textbf{b}\)의 색상 값이다. $\ell$을 통해 각 가능성의 품질을 정량화하고, 다음을 최소화하는 occupancy 값 \(\alpha_\textbf{p}\)를 구한다.

\[\begin{equation} \mathcal{L} (\textbf{p}) = \alpha_\textbf{p} \ell (L_\textbf{p}, L_\textrm{target}) + (1 - \alpha_\textbf{p}) \ell (L_\textbf{b}, L_\textrm{target}) \end{equation}\]

이 접근 방식은 색상 대신 두 표면의 loss를 혼합함으로써 대상 색상을 가장 잘 설명하는 표면을 선택한다.

여기에 제시된 단순화된 예는 후보 색상 \(L_\textbf{p}\)가 정적이라고 가정한다. 실제로 \(L_\textbf{p}\)는 최적화의 대상이 되며, 모호성을 해결하기 위해 여러 시점이 필요하다.

여러 표면 후보

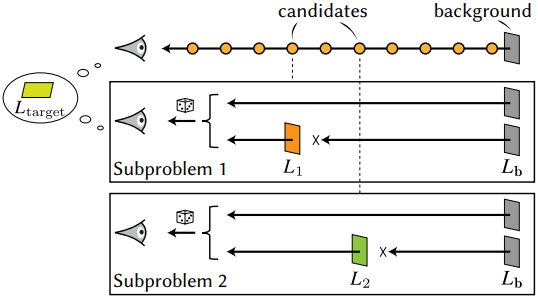
이제 loss 식을 확장하여 여러 후보를 고려하자. 이는 여러 perturbation의 효과를 동시에 평가할 수 있게 되어 수렴 속도가 빨라진다는 장점이 있다.

단일 후보 loss 식의 핵심 속성은 후보를 배경 표면에서 분리한다는 것이다 (즉, 둘 중 하나를 관찰). 여러 후보에 대한 일반화는 각 후보를 독립적인 하위 문제로 취급하여 각 loss의 합을 최소화함으로써 이 속성을 유지한다.

\[\begin{equation} \mathcal{L}_\textrm{ray} (\textbf{r}) = \sum_{i=1}^m \mathcal{L} (\textbf{p}_i) \end{equation}\]

공간-방향적인 loss

재구성 task는 큰 광선 집합 \(\{\textbf{r}_k\}_{k=1}^n\)를 따라 loss를 평가한다 ($n$은 모든 레퍼런스 이미지의 총 픽셀 수). 이는 독립적으로 고려되는 후보 표면 집합을 더욱 확장한다.

\[\begin{equation} \mathcal{L}_\textrm{total} = \sum_{k=1}^n \mathcal{L}_\textrm{ray} (\textbf{r}_k) \end{equation}\]

기존의 표면 최적화는 표면 자체에만 gradient를 전파하는 반면, \(\alpha_\textbf{p}\)와 \(L_\textbf{p}\)를 사용하면 관측된 3D 공간 전체를 포괄한다. 여러 방향에서 바라본 위치의 경우, loss는 일반적으로 방향에 따라 달라진다.

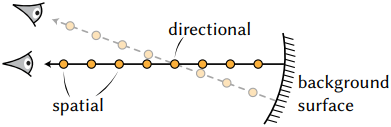
즉, $\ell$의 평가를 이미지 공간에서 장면으로 옮겨서 공간-방향적인 radiance field loss를 만들었다.

3. Stochastic background surface

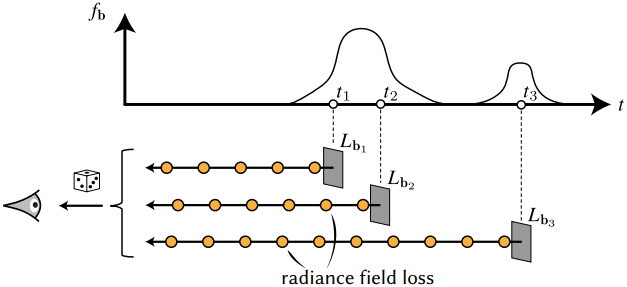
Loss function 도출을 완료하기 위해 남은 것은 배경 표면의 정의이다. 결정론적인 표면 대신, 광선별 분포 \(f_\textbf{b}\)에서 배경을 도출한다. 이를 통해 occupancy가 높은 영역에서 간헐적으로 visibility를 확보할 수 있으며, 가려진 물체를 배경으로 간주할 수 있다. 중요한 것은, 이를 통해 복잡한 위상적 변화를 명시적으로 고려하지 않고도 최적화 과정에서 복잡한 위상적 변화를 지원할 수 있다는 것이다.

분포 \(f_\textbf{b}\)의 설계는 유연하다. 한 가지 간단한 접근 방식은 occupancy가 높은 영역에서 샘플링을 우선시하는 것이다. 이러한 영역은 표면과 일치할 가능성이 더 높기 때문이다. 광선 순회 중에 occupancy를 기반으로 위치를 배경 표면으로 사용할지 여부를 확률적으로 결정한다. 이러한 순차적인 결정 과정은 free-flight distance 개념을 반영하여 free-flight 배경 분포를 형성한다.

Free-flight 분포에서 배경 표면을 샘플링할 수 있는 기대값을 계산하면 해당 집계된 local loss는 다음과 같이 도출된다.

\[\begin{equation} \mathcal{L}(\textbf{p}_i) = \left( \prod_{j=1}^{i-1} (1 - \alpha_{\textbf{p}_j}) \right) \alpha_{\textbf{p}_i} \ell (L_{\textbf{p}_i}) \end{equation}\]

이를 \(\mathcal{L}_\textrm{total}\) 식에 대입하면 radiance field loss가 도출된다.

Implementation

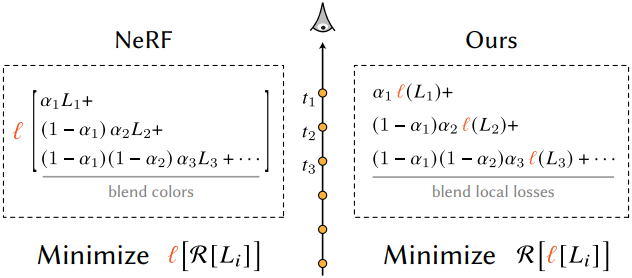
Loss function의 구현은 NeRF와 같은 표준 volumetric 재구성 방법의 색상 혼합 구조와 유사하게 구성될 수 있다. 따라서 기존 코드베이스에서 구현하기가 매우 간단하며, 이는 아래의 pseudocode 비교에서 확인할 수 있다.

또한, 이러한 유사성은 본 방법의 최적화 환경이 NeRF의 robustness를 계승하여 NeRF와 유사함을 시사한다. 그러나 NeRF의 loss function은 광선을 따라 모든 샘플을 블렌딩한 후 타겟 색상과 전체적으로 일치시키는 반면, 본 방법의 loss function은 각 샘플이 타겟 색상과 독립적으로 일치하거나 배경이 더 잘 일치할 경우 투명해지는 것을 목표로 한다. 이러한 차이점은 본 방법의 접근 방식을 표면 재구성 알고리즘으로 근본적으로 정의한다.

4. Volume relaxation

저자들은 본 방법의 휴리스틱 기반 일반화를 제안하였다. 이는 위 알고리즘과 직교하며 학습 과정에서 선택 사항이다.

표면 표현은 많은 장점을 제공하지만, 불투명 표면 가정은 특정 상황에서 본질적인 한계를 갖는다. 예를 들어, 서브픽셀 구조는 geometry로 모델링하기 어렵고, 단일 표면으로는 방향이 변하는 물질의 모양을 정확하게 표현하지 못할 수 있다. 이러한 영역에서는 volumetric 표현이 더 적합하다.

저자들의 아이디어는 대부분의 장면을 표면(loss가 낮은 영역)으로 재구성하고, 나머지 어려운 영역에만 volumetric 표현을 사용하도록 본 방법을 완화하는 것이다. 이를 위해 먼저 20,000 iteration의 학습을 통해 초기 표면 표현을 얻는다. 그런 다음, local loss가 높은 영역을 평가하여 어려운 영역을 식별한다. 이후 학습 단계에서는 표면 가정을 완화하여 이러한 영역에서 volumetric 알파 블렌딩을 허용한다.

학습 후에는 표면을 추출하는 대신, 표면 영역을 완전히 불투명한 “volume”으로 처리하여 장면을 volumetric하게 렌더링한다. NeRF로 최적화된 장면과 비교했을 때, 본 논문의 방법은 표면 영역의 컴팩트한 표현이라는 이점을 여전히 제공한다. 광선을 따라 색상을 누적할 때 투과율이 1이 되는데 필요한 샘플 수가 매우 적어 inference 속도가 빨라지고 학습 중 계산 리소스가 절감된다.

명시적으로 언급되지 않은 경우, 본 논문의 모든 결과는 volume relaxation 없이 학습되었다.

Experiments

1. Novel View Synthesis

다음은 시각적 품질을 NeRF와 비교한 결과이다.

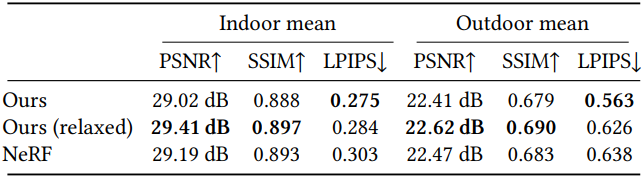
2. Geometry reconstruction

다음은 충분한 뷰에 대하여 학습된 간단한 장면의 예시이다. 학습 중에 Laplacian regularizer를 적용하면 표면이 부드러워져 최종 geometry가 더 정확해진다.

다음은 메쉬 추출 결과를 NeuS2와 비교한 결과이다.

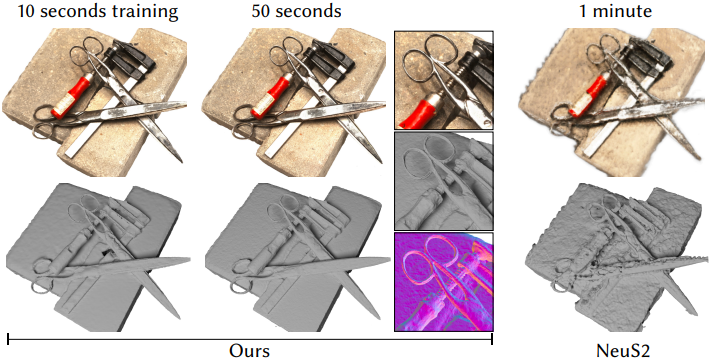
Limitations

1. View-dependent한 외형의 표면을 재구성하는 데 실패한다. Laplacian 가중치를 높이면 도움이 될 수 있지만, 기하학적 디테일 묘사가 억제된다.
2. 고주파 색상 변화는 volumetric 표현에 비해 정확하게 표현하기가 더 어렵다.