[논문리뷰] QuickSplat: Fast 3D Surface Reconstruction via Learned Gaussian Initialization
ICCV 2025. [Paper] [Page]
Yueh-Cheng Liu, Lukas Höllein, Matthias Nießner, Angela Dai
Technical University of Munich
8 May 2025

Introduction
최근 3D Gaussian Splatting (3DGS)은 멀티뷰 이미지를 입력으로 사용하여 사실적인 novel view synthesis를 달성하였다. 후속 연구들은 3DGS를 확장하여 정확한 표면 재구성도 얻었다. 그러나 이러한 방법들은 일반적으로 각 장면을 개별적으로 최적화한다. 즉, 대규모 실내 장면의 경우 30분 이상 걸릴 수 있는 gradient descent의 여러 iteration이 필요하다. 또한 표면은 관찰된 입력 이미지에서만 최적화되지만, 충분히 많은 다양한 이미지를 캡처하는 것은 큰 장면의 경우 여전히 어렵다. 따라서 결과 형상은 뷰 커버리지 또는 텍스처 정보가 적은 누락되거나 변형된 영역을 포함할 수 있다.
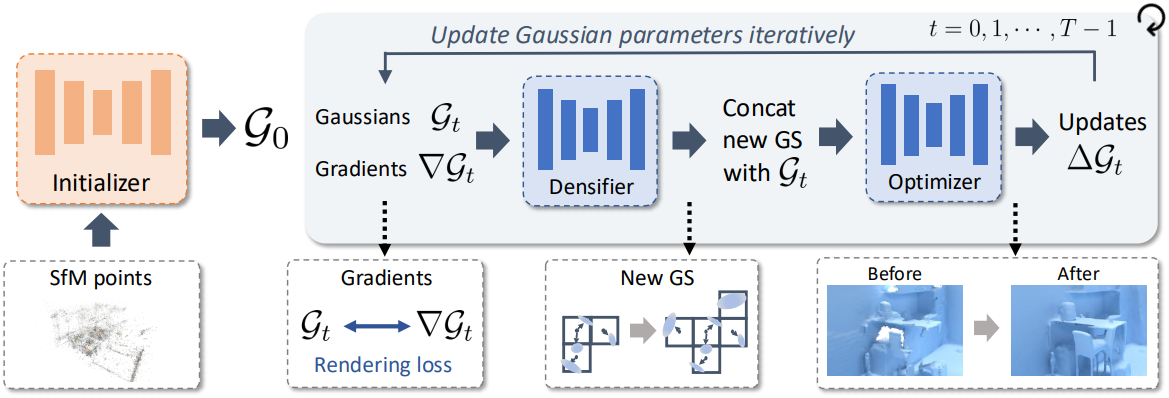
이를 위해, 3D 표면 재구성을 위한 새로운 일반화된 prior를 제안하였다. 이 방법은 2D Gaussian Splatting (2DGS) 기반 고충실도 재구성을 데이터로부터 재구성 prior를 학습하는 장점과 결합한다. 구체적으로, 최적화의 핵심 요소인 초기화, Gaussian 업데이트, 그리고 densification의 효율성을 향상시킨다. 이를 통해 장면별 최적화 시간을 획기적으로 단축할 수 있다. 또한, 본 논문에서 제안하는 prior는 고품질 실내 장면 형상을 최적화하도록 유도하여, 관측이 불충분하거나 텍스처가 없는 영역으로 인한 한계를 극복한다 (ex. 직선이 아닌 벽).
입력된 멀티뷰 이미지로부터 Gaussian 파라미터를 공동으로 생성하는 여러 sparse 3D CNN 기반 네트워크를 학습시킨다. Initializer는 입력 SfM 포인트 클라우드를 densify하여 장면의 관찰되지 않거나 텍스처가 없는 영역에 있는 큰 구멍을 완성한다. 그런 다음 새로운 Gaussian을 성장시키고 기존 Gaussian의 업데이트 벡터를 예측하는 새로운 densification-optimization 기법을 사용한다. Gradient descent optimizer와 유사하게, 이 기법을 여러 번 반복하여 Gaussian을 반복적으로 개선한다. 마지막으로, 렌더링된 depth map에서 TSDF fusion을 사용하여 수렴된 2D Gaussian들에서 표면을 추출한다. QuickSplat은 임의의 여러 뷰를 입력으로 하는 대규모 실제 실내 환경을 정확하게 재구성하며, 기존 방법보다 8배 더 빠르다.
Method
1. Surface Representation
장면 표현으로 2DGS를 채택하여 고품질 표면을 모델링할 수 있다. 구체적으로, 2D Gaussian 집합 \(\mathcal{G} = \{\textbf{g}_i\}_{i=1}^N\)을 사용하며, 각 Gaussian \(\textbf{g}_i \in \mathbb{R}^{14}\)는 3D 위치, scale, rotation, opacity, RGB diffuse color로 parameterize된다. 주어진 시점에서 장면을 렌더링하기 위해, 2DGS는 모든 Gaussian과 광선 간의 광선-splat 교차점을 계산한다. 그런 다음, 광선 $x$에 대한 픽셀 색상 $c$는 깊이 정렬된 splat 목록을 따라 알파 블렌딩을 사용하여 렌더링된다.
\[\begin{equation} c(x) = \sum_{i \in \mathcal{N}} c_i \alpha_i T_i, \quad \textrm{with} \quad T_i = \prod_{j=1}^{i-1} (1 - \alpha_j), \quad \alpha_i = o_i \textbf{g}_i^\textrm{2D}(\textbf{u}(x)) \end{equation}\]($c_i$는 광선을 따라 $i$번째 splat의 색상, $T_i$는 누적 투과율, \(\alpha_i\)는 opacity $o_i$와 교차점 $\textbf{u}(x)$에서의 2D Gaussian 값의 곱)
Gaussian은 관찰된 이미지 색상 $C$에 대한 렌더링 loss를 적용하여 최적화할 수 있다.
\[\begin{equation} \mathcal{L}_\textrm{c} (x) = 0.8 \| c(x) - C \|_1 + 0.2 (1 - \textrm{SSIM}(c(x), C)) \end{equation}\]\(\mathcal{L}_c\) 외에도 normal loss나 distortion loss와 같은 정규화 함수가 적용된다. 최적화 후, 모든 학습 뷰에서 depth map을 렌더링하고 TSDF fusion을 실행하여 메쉬 표면을 추출한다.
본 논문은 gradient descent를 사용하여 2D Gaussian들을 직접 최적화하는 대신, 신경망을 사용하여 $\mathcal{G}$를 예측하는 것을 제안하였다. 이를 위해, 그리드 구조에 2D Gaussian들을 정렬하여 예측을 용이하게 한다. 구체적으로, 장면을 크기가 \(\textbf{v}_d\)인 3D sparse voxel로 discretize하고 각 voxel에 latent feature \(\textbf{f} \in \mathbb{R}^{64}\)을 할당한다. 신경망은 이러한 sparse voxel의 feature를 예측한다. 그런 다음, 작은 MLP를 사용하여 이 feature들을 \(\textbf{v}_g\)개의 2D Gaussian으로 디코딩한다.
2. Initialization Prior
첫 번째 단계는 모든 Gaussian $\mathcal{G}$의 초기화를 만드는 것이다. 2DGS에 따라 SfM 포인트 클라우드에서 2D Gaussian을 초기화하고 그리드 구조에 맞춰 voxelize한다. 이는 연속적인 표면을 아직 표현하지 않고 많은 빈 영역을 포함하는 sparse한 Gaussian 집합을 생성한다. 따라서 기존 Gaussian 주변에 추가 Gaussian을 예측하여 표면 밀도를 높인다.
구체적으로, 추가 voxel feature를 예측하는 initializer \(\theta_I\)를 학습시킨다. SGNN에서 영감을 받은 이 네트워크는 인코더-디코더 아키텍처의 sparse 3D convolution으로 구성된다. Bottleneck에 있는 일련의 dense CNN block과 upsampling layer를 통해 sparse voxel의 밀도가 점진적으로 증가한다. Occupancy head는 voxel을 다음으로 높은 해상도에 할당해야 하는지 여부를 결정하는 threshold 역할을 한다. Sparse voxel 출력을 생성하는 SGNN과 달리, 본 논문에서는 디코더 MLP를 사용하여 voxel latent feature를 2D Gaussian으로 해석한다. 각 Gaussian 속성에 대해 서로 다른 activation function을 사용한다.
위치 \(\textbf{g}_c \in \mathbb{R}^3\)는 voxel 중심 \(\textbf{v}_c \in \mathbb{R}^3\)에 대하여 정의된다.
\[\begin{equation} \textbf{g}_c = \textbf{v}_c + R (2 \sigma (x) - 1) \end{equation}\]($R = 4 v_d$는 Gaussian이 존재할 수 있는 voxel 주위의 반지름, $\sigma$는 sigmoid function)
PixelSplat의 reparameterization trick에서 영감을 받아, opacity \(\textbf{g}_o \in \mathbb{R}\)는 마지막 upsampling layer 이후의 occupancy이다. 이를 통해 렌더링 loss가 upsampling layer로 역전파되어 마지막 업샘플링 프로세스에서 어떤 점을 유지할지 제어할 수 있다. Scale 파라미터에는 softplus 함수를, 색상에는 sigmoid 함수를 사용하며, rotation quaternion 벡터는 정규화한다.
Initializer는 여러 loss로 학습된다. 먼저, 렌더링 loss \(\mathcal{L}_\textrm{c}\)로 예측된 Gaussian의 품질을 학습시킨다. 그러나 빈 영역에 대한 신호는 제공하지 않는다. 즉, initializer는 Gaussian을 densify하고 모든 구멍을 닫아야 하지만 렌더링 loss는 빈 voxel로 backpropagation되지 않는다.
이를 위해 GT 형상에 대해 voxel grid의 occupancy도 학습시킨다. 레이저 스캔의 메쉬 형상을 포함하는 ScanNet++의 장면에서 네트워크를 학습시킨다. 이를 통해 SGNN 아키텍처의 모든 upsampling layer 전에 occupancy loss \(\mathcal{L}_\textrm{occ}\)를 계산할 수 있다. \(\mathcal{L}_\textrm{occ}\)는 각 voxel의 occupancy에 대한 binary cross-entropy loss로 계산된다. 이는 새로운 voxel을 할당해야 하는 추가 신호를 제공한다.
추가로 모든 학습 뷰에 대해 렌더링된 깊이와 메쉬의 깊이 사이의 L1 거리를 측정하는 depth loss \(\mathcal{L}_\textrm{d}\)를 계산한다. 또한, 2D Gaussian을 실제 표면과 더욱 일치시키기 위해, Gaussian normal \(\textbf{n}_g\)가 메쉬 normal \(\textbf{n}_m\)과 같아지도록 normal loss $\mathcal{L}_\textrm{n}$을 추가한다. \(\textbf{n}_g\)는 2D Gaussian에 수직인 방향으로 정의된다.
\[\begin{equation} \mathcal{L}_\textrm{n} = 1 - \textbf{n}_g^\top \textbf{n}_m \end{equation}\]Initializer 학습을 위한 전체 loss는 다음과 같다.
\[\begin{equation} \mathcal{L} (\theta_I) = \mathcal{L}_\textrm{c} + \mathcal{L}_\textrm{d} + \mathcal{L}_\textrm{occ} + 0.01 \mathcal{L}_\textrm{n} + 10 \mathcal{L}_\textrm{dist} \end{equation}\](\(\mathcal{L}_\textrm{dist}\)는 distortion loss)
3. Iterative Gaussian Optimization
Initializer는 SfM 포인트들을 입력으로 사용하여 더 밀도가 높은 Gaussian을 예측한다. 네트워크는 렌더링 loss를 고려하여 학습되지만, 입력은 색상이 있는 SfM 포인트들뿐이다. 표면 재구성을 더욱 개선하기 위해, 현재 Gaussian들의 품질에 대한 정보도 입력에 포함시키고자 한다.
구체적으로, 학습 이미지를 렌더링하고 여러 시점에 걸쳐 누적된 latent voxel feature에 대한 렌더링 loss의 gradient $\nabla \mathcal{G}$를 계산한다. 이 gradient에는 Gaussian을 어떻게 조정해야 개선될 수 있는지를 나타내는 신호가 포함되어 있다.
Optimizer
G3R에서 영감을 받아, \(\{\mathcal{G}, \nabla \mathcal{G}\}\)를 입력으로 하여 모든 voxel에 대한 업데이트를 예측하는 optimizer \(\theta_O\)를 학습시킨다.
\[\begin{equation} f_{\theta_O} (\mathcal{G}_t, \nabla \mathcal{G}_t, t) = \Delta \mathcal{G}_t \end{equation}\](\(\Delta \mathcal{G}_t\)는 모든 latent voxel feature에 대한 예측된 업데이트)
G3R과 유사하게, 이 과정을 여러 timestep $t$에 걸쳐 구성한다. 즉, \(\nabla \mathcal{G}_t\)를 반복적으로 계산하고, \(\Delta \mathcal{G}_t\)를 예측하고, 표현을 \(\mathcal{G}_{t+1} = \mathcal{G}_t + \Delta \mathcal{G}_t\)로 업데이트한다. \(\theta_O\)를 위해 sparse 3D UNet 아키텍처를 활용한다. 업데이트가 오버슈팅되지 않도록 출력을 정규화한다.
Densifier
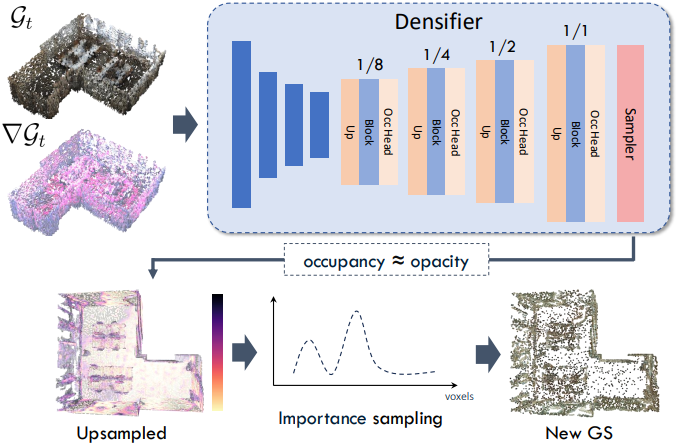
SfM 포인트 클라우드는 initializer에 의해 밀도가 높아지지만, 여전히 빈틈이 있을 수 있다. 표면 재구성의 이러한 빈틈은 \(\theta_O\)에 의해 채워지지 않을 수 있는데, 예측된 업데이트가 voxel 중심을 기준으로 Gaussian을 이동할 뿐, 새로운 voxel을 할당하지 않기 때문이다. 이러한 빈틈은 표면 재구성의 품질을 현저히 저하시킨다.
이를 위해, 자유 공간에서 추가적인 voxel feature를 예측하는 densifier 네트워크 \(\theta_D\)를 도입한다. Densifier는 initializer \(\theta_I\)의 디자인을 따르지만, $\nabla \mathcal{G}$와 $t$를 추가 입력으로 제공한다.
\[\begin{equation} f_{\theta_D} (\mathcal{G}_t, \nabla \mathcal{G}, t) = \hat{\mathcal{G}}_t \end{equation}\](\(\hat{\mathcal{G}}_t\)는 예측된 추가 voxel feature)
이를 통해 gradient가 큰 영역을 사용하여 densification이 가능한 위치를 파악할 수 있다. 또한, bottleneck에 dense block들을 사용하지 않음으로써 추가 voxel의 위치가 기존 voxel과 인접하도록 제한한다. 이렇게 하면 추가 Gaussian을 증가시켜야 하는 위치를 더 잘 제한하기 때문에 더 효과적이다.
마지막으로, 임의의 수의 새로운 Gaussian을 예측하는 대신, 학습 중에 Gaussian의 수와 메모리 사용량을 제어하기 위해 중요도 샘플링 (importance sampling)을 수행한다. 핵심 아이디어는 디코더에서 생성된 다른 후보들 중에서 성장시킬 opacity 값이 더 높은 Gaussian을 선택하는 것을 우선시하는 것이다. 왜냐하면 이 Gaussian은 표면 형상에 더 많이 기여하기 때문이다. Occupancy를 opacity로 해석함으로써, 마지막 upsampling layer 이후에 occupancy 예측에 의해 가중치가 적용된 추가 voxel을 샘플링할 수 있다.
현재 iteration에서 추가할 수 있는 voxel 수를 $n(t) = s / 2^t$로 정의한다 ($s$ = 20,000). 즉, 초기 timestep에 대해 더 densify한 다음 점차 새로운 voxel 수를 줄인다. Inference 시에는 occupancy 예측에서 상위 $n(t)$개의 복셀을 선택한다.
이 방법의 장점은 휴리스틱에 기반한 densification 전략을 설계할 필요가 없다는 것이다. Optimizer를 사용하여 densifier를 end-to-end로 학습시킴으로써, 현재 Gaussian 상태와 그 gradient를 새롭고 기여를 많이하는 Gaussian으로 매핑하는 방법을 학습시킨다.
Densification-Optimization Loop
Densification-optimization 루프에서는 \(\theta_D\)와 \(\theta_O\) 두 네트워크 모두를 활용하여 여러 timestep에 걸쳐 latent voxel feature를 성장시키고 개선한다.
- Voxel을 Gaussian 파라미터로 디코딩하고, 모든 학습 이미지를 렌더링한 후 \(\nabla \mathcal{G}_t\)를 계산한다.
- Densifier가 추가 voxel 위치 \(\hat{\mathcal{G}}_t\)를 예측한다.
- 기존 voxel feature와 새로운 voxel feature를 \(\bar{\mathcal{G}}_t = \mathcal{G}_t \cup \hat{\mathcal{G}}_t\)로 concat한다.
- 새로운 voxel의 기울기를 0으로 초기화하여 유사하게 \(\nabla \bar{\mathcal{G}}_t\)를 얻는다.
- Optimizer가 업데이트 \(\Delta \bar{\mathcal{G}}_t\)를 예측하고, \(\mathcal{G}_{t+1} = \bar{\mathcal{G}}_t + \Delta \bar{\mathcal{G}}_t\)를 얻는다.
End-to-End Training
두 번째 학습 단계에서는 densifier \(\theta_D\)와 optimizer \(\theta_O\)를 함께 학습시킨다. 이 단계에서 initializer \(\theta_I\)는 고정된다. 마찬가지로 densifier의 중간 upsampling layer에서 \(\mathcal{L}_\textrm{occ} (\theta_D)\)를 계산한다. 또한, 업데이트된 voxel feature \(\mathcal{G}_{t+1}\)을 Gaussian으로 디코딩하고 렌더링 loss를 계산한다.
\[\begin{equation} \mathcal{L}(\theta_O) = \mathcal{L}_\textrm{c} + \mathcal{L}_\textrm{d} + 10 \mathcal{L}_\textrm{dist} \end{equation}\]$T = 5$ timestep 동안 densification-optimization 루프를 실행하고 각 timestep마다 loss를 계산한다. G3R과 유사하게, 이후 timestep에 대한 loss의 gradient를 분리하여, 각 timestep을 개별적으로 최적화한다.
Experiments
- 데이터셋: ScanNet++
- 구현 디테일
- $v_d$ = 4cm, $v_g$ = 2
- initializer와 densifier는 4개의 up/downsampling layer를 사용
- optimizer는 G3R을 따라 UNet 아키텍처
- learning rate: $10^{-4}$
- $\nabla \mathcal{G}$는 100개의 학습 이미지에 대하여 계산
- RTX A6000 GPU 1개에서 3일 학습
1. Comparison to State of the Art
다음은 다른 방법들과 비교한 결과이다.

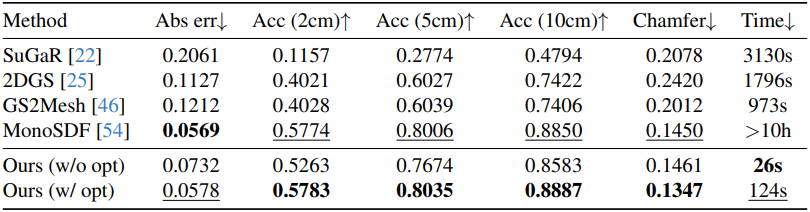
다음은 MonoSDF와 정성적으로 비교한 결과이다.

2. Ablations
다음은 ablation study 결과이다.
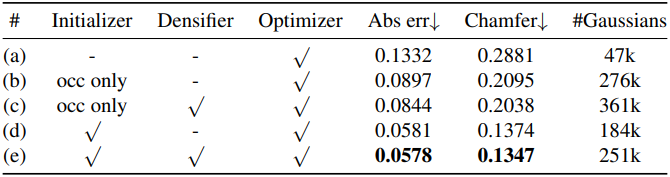

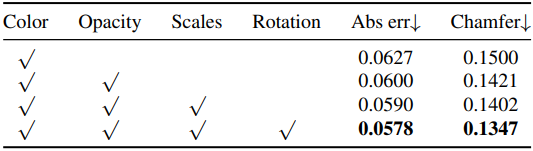
다음은 initializer 출력에 대한 ablation 결과이다.
Limitations
- 거울 반사에 어려움을 겪는다.
- 정적인 환경을 가정하기 때문에 동적 장면을 재구성할 수 없다.
- 최적화 런타임을 크게 단축했지만, 아직 실시간으로 재구성할 수 없다.