[논문리뷰] Quantile Rendering: Efficiently Embedding High-dimensional Feature on 3D Gaussian Splatting

arXiv 2025. [Paper]
Yoonwoo Jeong, Cheng Sun, Frank Wang, Minsu Cho, Jaesung Choe
NVIDIA | POSTECH
24 Dec 2025

Introduction

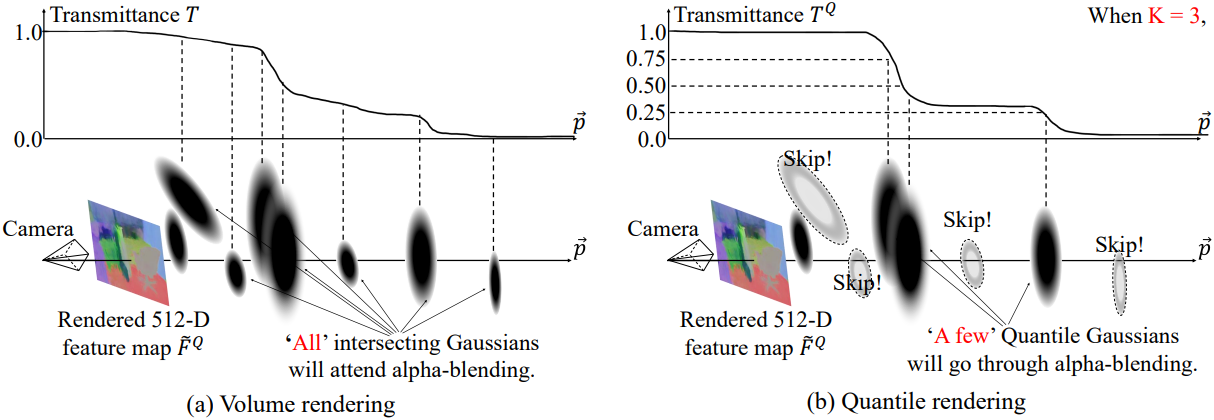
기존의 볼륨 렌더링 알고리즘은 출력에 대한 실제 기여도와 관계없이 광선과 교차하는 모든 Gaussian을 샘플링한다. RGB 렌더링의 경우 이러한 오버헤드는 감당할 수 있지만, 512차원 CLIP feature와 같은 고차원 임베딩의 경우 계산량이 과중해진다. 이 문제를 해결하기 위해 여러 논문에서 512차원 CLIP feature의 차원을 3차원 또는 6차원이나 codebook으로 압축하는 방법을 제시했다. 이러한 전략은 효과적이지만 근본적인 해결책은 아니며, 고차원 feature에 저장된 원래 정보를 손실할 가능성이 있다. 또한, 최적화된 3D Gaussian은 장면별 최적화 방식으로 인해 노이즈가 많거나 local minima를 가질 수 있다. 따라서 이러한 3D Gaussian 위에 고차원 feature 벡터를 적절하게 임베딩하는 것은 어려운 과제이다.

저자들은 모든 Gaussian이 영향력이 있는 것은 아니며, 3D Gaussian 중 일부만이 광선을 따라 고차원 feature 렌더링에 의미 있는 영향을 미친다는 가설을 세웠다. 이를 토대로 고차원 Gaussian feature를 위한 효율적인 렌더링 알고리즘인 Quantile Rendering (Q-Render)를 개발했다. Q-Render는 rasterization된 모든 3D Gaussian을 촘촘하게 누적하는 대신, 광선의 투과율 프로파일을 지배하는 소수의 Quantile Gaussian들을 적응적으로 선택하여 이러한 Quantile Gaussian만을 렌더링한다. 이러한 quantile 기반 선택은 중복 계산을 줄이고, 고차원 feature map 렌더링이 필요한 후속 task에 필요한 원본 신호를 근사화한다.

본 논문에서는 Q-Render를 3D 신경망에 통합하여 3D Gaussian을 기반으로 Gaussian feature를 예측하는 GS-Net을 구축했다. Q-Render는 2D 학습과 3D 신경망 사이의 효율적인 연결 고리 역할을 하며, 이미지 공간 loss function에서 3D 신경망의 예측값으로 backward gradient가 흐르도록 한다. 또한, 이러한 통합을 통해 Q-Render의 sparse한 샘플링 특성이 더욱 효과적으로 활용된다. 3D 신경망의 inductive bias는 공간적으로 매끄러운 Gaussian feature를 예측하는 경향이 있으므로, 각 광선을 따라 모든 Gaussian을 dense하게 샘플링할 필요가 없다. 대신, sparse하게 선택된 Quantile Gaussian만으로도 고차원 feature map을 충실하게 렌더링할 수 있으며, 렌더링 과정과 backward 계산 과정에서 발생하는 연산 오버헤드를 크게 줄일 수 있다.

Method

최적화된 3D Gaussian \(\mathcal{G} = \{\textbf{g}_i\}_{i=1}^N\)이 주어졌을 때, 3D 신경망은 $C$차원의 Gaussian feature \(\mathcal{F} = \{\textbf{f}_i\}_{i=1}^N\)을 예측한다. 본 논문에서 제시하는 Quantile Rendering을 통해, Gaussian feature는 $C$차원의 feature map으로 렌더링된다. 3D 신경망은 렌더링된 feature map과 CLIP의 비전 인코더에서 추출한 2D feature map 간의 렌더링 loss를 최소화하도록 학습된다.

1. 3D neural network

포인트 클라우드 처리를 위한 기존의 3D 신경망은 장면 규모의 3D 포인트를 효율적으로 처리하기 위해 3D 포인트를 voxelize하는 방식을 사용한다. 이러한 신경망은 흩어진 포인트들을 고유한 공간적 위치를 가진 sparse voxel grid로 변환하여, 효율성을 바탕으로 전체 3D 장면에 대한 single-pass inference를 가능하게 한다.

포인트 클라우드 처리와 달리, 연속적인 3D Gaussian으로 장면을 모델링할 경우 중첩 영역이 발생한다. 이 문제를 해결하기 위해, 본 논문에서는 3D Gaussian의 중심 위치 $\mu$를 샘플링하여 voxelization을 적용하는 SplatFormer 방식을 채택했다. 이는 일반적인 3D backbone인 Point Transformer v3 (PTv3), MinkUnet과의 호환성을 보장하기 위함이다. 이러한 모델들은 voxel feature를 예측하도록 설계되었으며, 예측된 voxel feature를 렌더링에 사용될 예측 Gaussian feature $\mathcal{F}$으로 변환하는 de-voxelization 단계를 진행한다.

2. Quantile rendering

2D foundation model의 지식을 활용하여 3D 신경망을 학습시키려면 렌더링 과정이 필수적이다. 볼륨 렌더링을 사용하면 고차원 Gaussian feature를 렌더링할 때 상당한 연산 능력이 요구될 수 있다. 이는 볼륨 렌더링이 광선을 따라 고차원 Gaussian feature $\mathcal{F}$를 반복적으로 누적하기 때문이다. $N$을 각 픽셀에 대한 Gaussian 개수, $C$를 feature 차원이라고 하면, 볼륨 렌더링의 시간 복잡도는 $\mathcal{O}(NC)$이다.

저자들은 이 문제를 해결하기 위해 quantile 기반 샘플링 전략을 도입하였다. Quantile은 sparse하면서도 대표성을 갖는 샘플링을 가능하게 한다. Quantile Rendering은 기존 볼륨 렌더링에서 신중하게 선택된 Gaussian의 분포를 부분집합으로 근사화함으로써, 대표성을 유지하면서 효율적인 렌더링을 구한다.

먼저, 3D Gaussian을 rasterization하고 splatting하여 각 픽셀 광선 $\vec{p}$에 대한 3D Gaussian 인덱스 $I$를 얻는다. 그런 다음, Q-Render는 Quantile Gaussian 샘플링, 알파 블렌딩, feature 정규화의 세 가지 하위 단계를 실행하여 각 광선을 따라 $K$개의 Quantile Gaussian을 샘플링한다 ($K$는 hyperparameter).

Quantile Gaussian 샘플링

Hyperparameter $K$가 주어졌을 때, 투과율 \(T \in \mathbb{R}_{[0,1]}\)을 각 광선에서 $K+1$개의 균등한 세그먼트로 나누고, 각 Gaussian을 통과하면서 투과율이 얼마나 변하는지 추적한다. 세그먼트 경계를 통과하면, 해당 Gaussian을 해당 구간의 Quantile Gaussian으로 결정한다.

Quantile Gaussian에 대한 알파 블렌딩

상대적으로 큰 투과율 변화를 보이는 이러한 Quantile Gaussian을 알파 블렌딩에 활용한다. 이러한 선택적 알파 블렌딩은 시간 복잡도를 $\mathcal{O}(NC)$에서 $\mathcal{O}(N+KC)$로 줄인다.

Feature 벡터 정규화

볼륨 렌더링에서 투과율 $T$는 1로 초기화되고, 이후 광선을 따라 알파 블렌딩이 진행됨에 따라 남은 투과율 $T$는 0에 가까워진다. 그러나 서브샘플링된 Gaussian에 대한 알파 블렌딩은 상대적으로 높은 투과율을 남길 수 있다. 최종 투과율 값이 0에 가까운 원래 분포를 반환하는 볼륨 렌더링을 근사화하기 위해, 누적 feature \(\tilde{\textbf{f}}^Q\)를 정규화하여 최종 투과율 $T^Q$를 강제로 0으로 설정한다.

\[\begin{equation} \tilde{\textbf{f}}^Q = \frac{\textbf{f}^Q}{1 - T^Q} \end{equation}\]

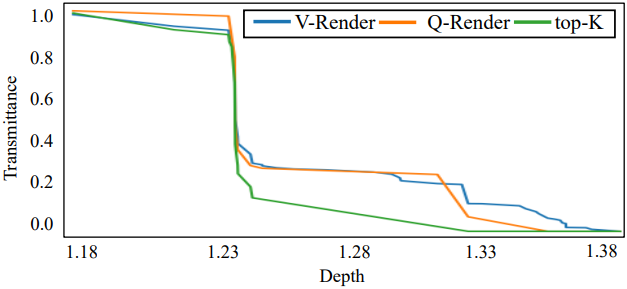
위 그림에서 볼 수 있듯이, Q-Render는 볼륨 렌더링에서 투과율 경향을 잘 근사하는 반면, top-$K$ 샘플링 전략은 다른 경향을 보인다. Q-Render는 오버헤드를 줄이면서 효율성과 정확도 모두에서 top-$K$보다 우수한 성능을 보여준다.

볼륨 렌더링에 대한 Q-Render의 근사 오차는 상한이 $\mathcal{O}(1/K)$이다.

증명)

---

카메라 광선 $t \in [0, \infty)$에 대한 볼륨 렌더링 적분 식은 다음과 같다. $$ \begin{equation} C_\textrm{vol} = \int_0^\infty c(t) \sigma (t) T(t) dt, \quad T(t) = \exp \left( - \int_0^t \sigma (s) ds \right) \end{equation} $$ 치환적분을 통해 적분 식을 투과율 $u = T(t)$에 대하여 표현할 수 있다. ($du = - \sigma (t) T(t) dt$) $$ \begin{equation} C_\textrm{vol} = \int_{u=1}^0 c(u) (-du) = \int_0^1 c(u) du \end{equation} $$ Q-Render는 투과율 도메인 $[0, 1]$을 다음과 같이 분할한다. $$ \begin{equation} 0 = u_{K+1} < u_K < \cdots < u_1 < u_0 = 1 \end{equation} $$ 각 $[u_{k-1}, u_k]$에 대해 Q-render는 투과율이 오른쪽 끝점 $u_k$과 교차하는 Gaussian을 선택한다. 따라서 알고리즘은 $u_k$에서 $c(u)$를 평가하며, 볼륨 렌더링 식에 대해 Right Riemann Sum을 정확하게 구현한다. $$ \begin{equation} C_Q^\textrm{right} = \sum_{k=1}^{K+1} c(u_k) \Delta u \end{equation} $$ $c(u)$는 미분 가능하며, 모든 $u \in [0, 1]$에 대하여 $\vert c'(u) \vert \le M$을 만족하는 $M$이 존재한다. 따라서 Right Rule error bound를 계산하면 다음과 같다. $$ \begin{equation} \vert C_\textrm{vol} - C_Q^\textrm{Right} \vert \le \frac{M (1 - 0)^2}{2(K+1)} = \frac{M}{2(K+1)} \end{equation} $$ Q-Render는 마지막에 정규화를 수행한다. ($T_Q$는 $K$개의 Quantile Gaussian을 처리하고 남은 투과율) $$ \begin{equation} \tilde{C}_Q = \frac{C_Q^\textrm{right}}{1 - T_Q} \end{equation} $$ 각 quantile이 적어도 $\Delta u$ 만큼 투과율을 제거하므로 다음이 성립한다. $$ \begin{equation} T_Q \le \Delta u = \frac{1}{K+1} \\ \frac{1}{1 - T_Q} \le \frac{1}{1 - \frac{1}{K+1}} = \frac{K+1}{K} \end{equation} $$ 정리하면 근사 오차는 다음과 같다. $$ \begin{equation} \vert C_\textrm{vol} - \tilde{C}_Q \vert \le \frac{K+1}{K} \cdot \frac{M}{2 (K+1)} = \frac{M}{2K} \end{equation} $$ 즉, 근사 오차의 상한은 $\mathcal{O}(1/K)$이다.

---

또한, 3D 신경망의 inductive bias는 공간적으로 부드러운 Gaussian feature 예측을 촉진한다. 따라서 광선을 따라 dense한 샘플링을 렌더링하는 것은 불필요해진다. Q-Render는 렌더링 및 backward pass 모두에서 계산 오버헤드를 크게 줄이면서도 높은 정확도의 feature 매핑을 수행하기에 충분하다.

3. Training loss

본 논문에서는 ScanNet 데이터셋과 LeRF-OVS 데이터셋 두 가지를 사용하여 open-vocabulary 3D semantic segmentation task에서 GS-Net의 성능을 검증하였다. 기존 연구들을 따라, CLIP 비전 인코더의 feature 벡터를 distillation 타겟으로 사용한다. 먼저 Grounded-SAM2를 사용하여 마스트 \(\{\textbf{m}\}\)을 추출하고, 해당 마스크에서 CLIP 임베딩 $\textbf{f}^\textrm{CLIP}$을 추출한다.

학습 데이터 쌍 \(\{\textbf{m}_i, \textbf{f}_i^\textrm{CLIP}\}\)이 주어졌을 때, 3D 신경망은 렌더링된 feature 벡터 \(\tilde{\textbf{f}}^Q\)와 CLIP 임베딩 \(\textbf{f}^\textrm{CLIP}\) 간의 차이를 최소화하도록 학습되며, 이는 다음과 같은 contrastive loss의 형태로 표현된다.

\[\begin{equation} \mathcal{L} = -\log \frac{\exp (\textrm{sim} (\tilde{\textbf{f}}^Q, \textbf{f}_i^\textrm{CLIP}))}{\sum_{i \ne j} \exp (\textrm{sim} (\tilde{\textbf{f}}^Q, \textbf{f}_j^\textrm{CLIP}))} \end{equation}\]

($\textrm{sim}(\cdot, \cdot)$은 cosine similarity)

Experiments

1. ScanNet dataset

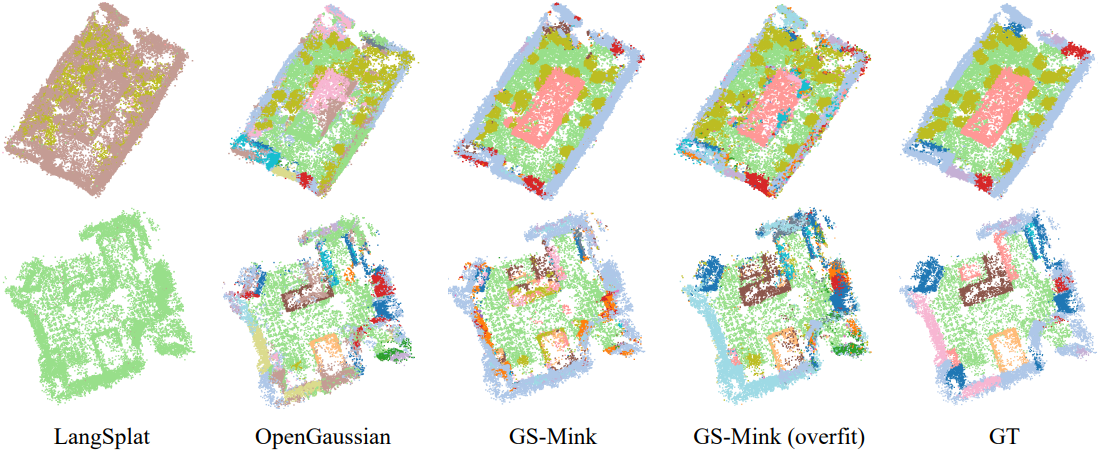
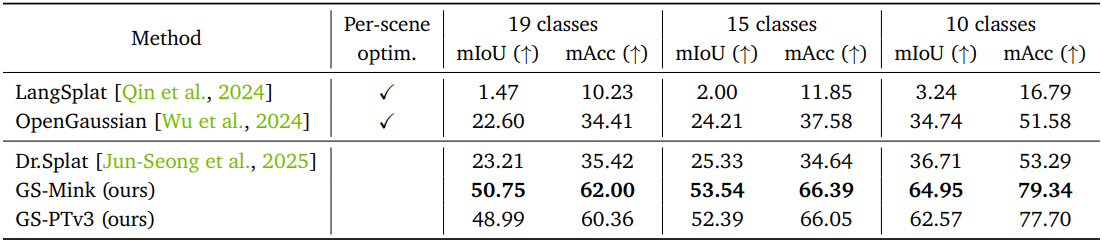
다음은 ScanNet 데이터셋에 대한 open-vocabulary 3D semantic segmentation 성능을 비교한 결과이다.

2. LeRF-OVS dataset

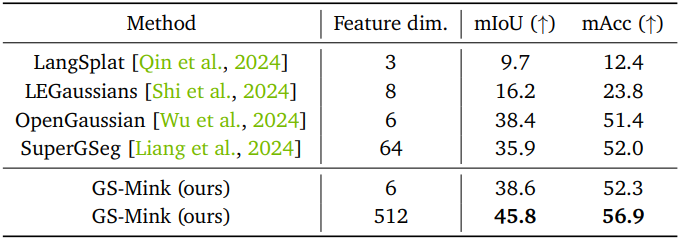
다음은 LeRF-OVS 데이터셋에 대한 open-vocabulary 3D semantic segmentation 성능을 비교한 결과이다.

3. Control experiments

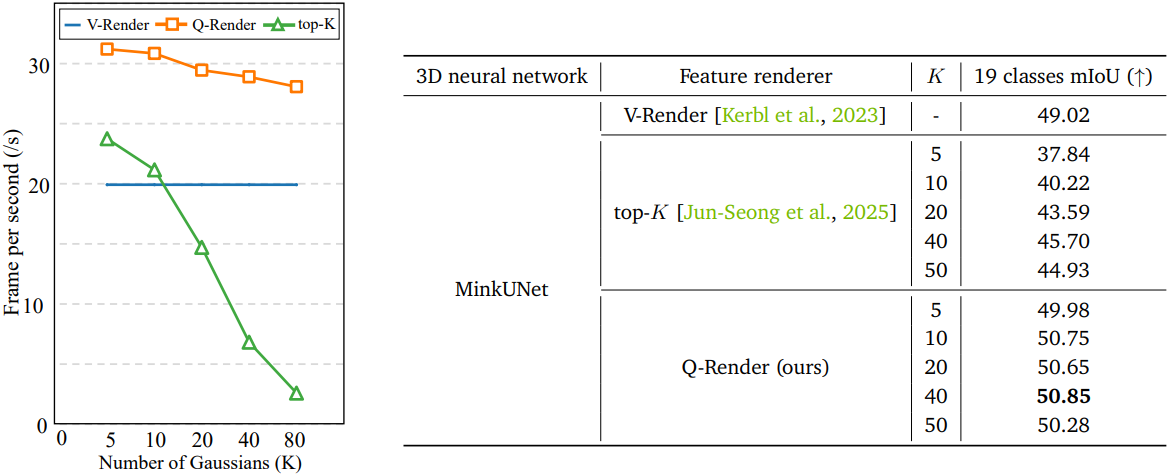
다음은 FPS와 mIoU를 렌더링에 참여한 Gaussian 수에 따라 비교한 결과이다.

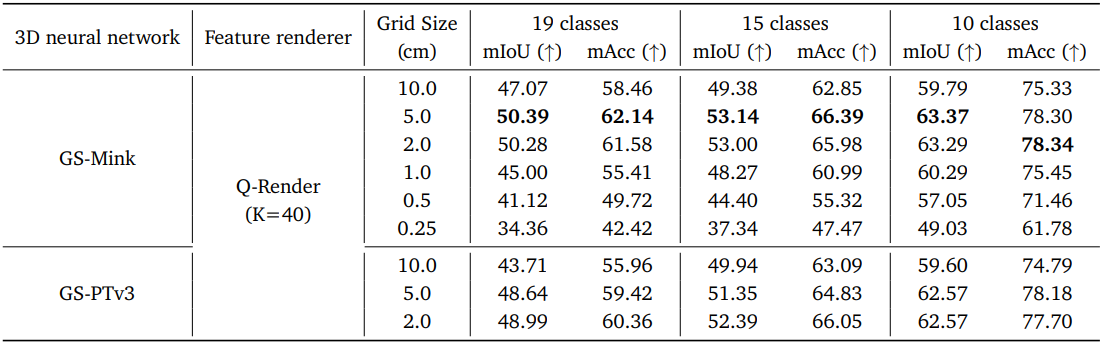
다음은 grid 크기에 대한 ablation study 결과이다.

다음은 렌더링 속도에 대한 비교 결과이다. (ScanNet scene0006_00, frame 0)

다음은 Gaussian을 de-voxelization한 결과와 de-voxelization 없이 렌더링한 결과를 비교한 예시이다.

Limitations

1. 학습에 사용한 $K$를 사용하지 않으면 성능이 크게 저하된다.
2. 3DGS가 최적화한 장면과 3D 신경망에 크게 의존한다.