[논문리뷰] Qonvolution: Towards Learning High-Frequency Signals with Queried Convolution

arXiv 2025. [Paper] [Page]
Abhinav Kumar, Tristan Aumentado-Armstrong, Lazar Valkov, Gopal Sharma, Alex Levinshtein, Radek Grzeszczuk, Suren Kumar
Samsung Research America | Samsung Research
15 Dec 2025

Introduction

고주파 신호를 학습하려는 task에는 크게 두 가지 유형이 있다. 첫 번째 유형은 novel view synthesis (NVS)로, MLP를 사용하여 신호를 직접 학습시킨다. 그러나 MLP는 대부분의 1D 및 2D 신호에 내재된 로컬 의존성을 포착하는 데 필요한 inductive bias가 부족하다. 기존 MLP 네트워크는 데이터 포인트나 픽셀을 개별적으로 처리하기 때문에 이러한 로컬 연결을 간과하는 경우가 많아 고주파 신호를 완벽하게 표현하는 데 한계가 있다.

두 번째 유형은 저주파 신호가 주어졌을 때, 2D super-resolution (SR)과 같이 저주파 신호를 CNN과 convolution하여 로컬 정보를 활용하는 방식이다. 하지만 이러한 접근 방식은 입력 query에 포함된 정보(ex. 공간 좌표)를 출력 고주파 신호 예측에 활용하지 않는 경우가 많다. CNN과 같이 로컬성을 가지는 아키텍처는 간단한 좌표 변환조차 요구하는 task에서 종종 실패한다.

기존 방법의 한계를 극복하고 이웃 의존성, 유용한 저주파 신호 및 query를 효과적으로 활용하기 위해 본 논문에서는 query 기반 convolution인 Qonvolution을 제안하였다. Qonvolution은 기본 구성 요소로서, 기존 MLP의 linear layer를 convolutional layer로 대체하고 저주파 신호와 함께 쿼리를 처리한다. 저주파 신호를 query와 convolution하는 이 접근 방식은 신경망 분야의 기존 방법론과 차별화된다.

본 논문에서는 1D regression, 2D SR, 2D residual image regression, NVS를 포함한 다양한 고주파 학습 task에서 Qonvolution Neural Network (QNN)을 평가하였다. 광범위한 실험 결과, QNN이 기존의 모든 baseline 모델보다 훨씬 우수한 성능을 일관되게 보여주었다. 특히, 3DGS을 사용하는 QNN은 까다로운 NVS task에서 Zip-NeRF 모델보다 우수한 성능을 보였으며, 학습 속도 또한 Zip-NeRF보다 빨랐다.

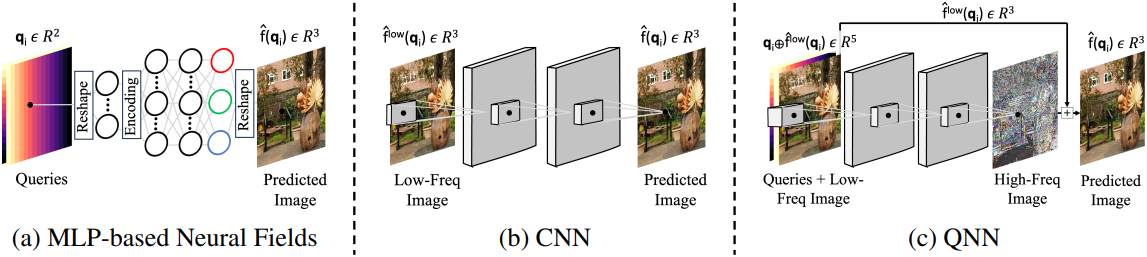
Method

\(\hat{f}^\textrm{low}\)와 \(f^\textrm{low}\)를 각각 실제 신호 $f$의 학습된 저주파 근사값과 GT 저주파 근사값이라고 하자. 이 저주파 신호는 특정 task들에서 종종 사용 가능하다. 예를 들어, NVS task는 splatting된 3DGS 이미지를 학습된 저주파 신호로 사용할 수 있으며, SR task 자체는 GT low-pass 이미지를 입력으로 사용한다.

저자들은 인접 좌표의 저주파 근사값을 제공하는 것이 유익할 것이라는 가설을 세웠다. 따라서, 주어진 query $\textbf{q}$의 이웃에 존재하는 정보, 즉 query 값과 해당 저주파 근사값을 활용하는 신경망을 설계하고자 했다. QNN은 인코딩된 입력 query의 이웃 \(\gamma(\textbf{q}_{\mathcal{N}(i)})\)와 해당 저주파 신호 \(\hat{f}_{\mathcal{N}(i)}^\textrm{low}\)를 concat한 후, 이들을 convolution하여 출력 \(\hat{f}_\theta (\textbf{q}_i)\)를 생성한다. 여기서 $\mathcal{N}(i)$는 인덱스 $i$의 이웃(자신 포함)을 나타낸다.

\[\begin{equation} \hat{f}_\theta^\textrm{QNN} (\textbf{q}_i) = \textrm{CNN} (\gamma (\textbf{q}_{\mathcal{N}(i)}) \oplus \hat{f}_{\mathcal{N}(i)}^\textrm{low}) \end{equation}\]

QNN 아키텍처의 뚜렷한 장점은 좌표별로 평가하는 대신 전체 신호에 대해 한 번만 평가하면 된다는 점이다. 하지만 단점은 NeRF에서 하나의 광선을 casting하는 것과 같이 이웃 영역이 없는 task에는 QNN을 사용할 수 없다는 것이다. 또한 QNN 아키텍처는 query 선택 및 통합에 있어 상당한 유연성을 제공하며, task에 따라 다양한 query를 추가할 수 있다.

Experiments

1. 1D Regression

다음은 1D regression에 대한 비교 결과이다.

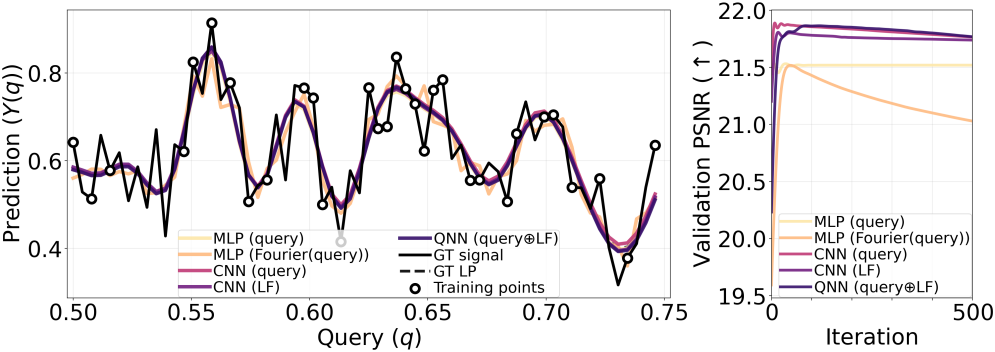
2. 2D Image Super-Resolution (SR)

다음은 2D SR에 대한 비교 결과이다.

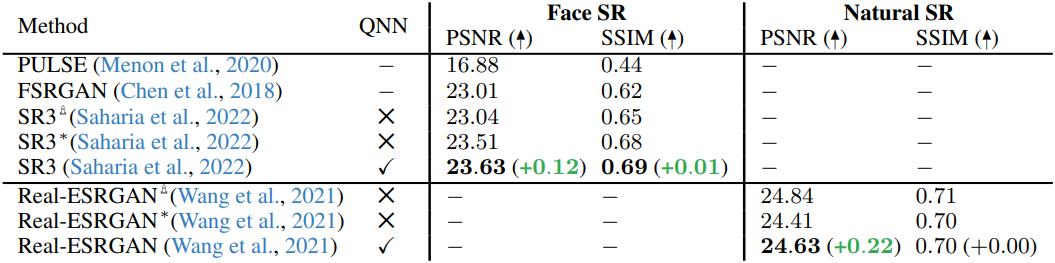
3. 2D Residual Image Regression

다음은 2D residual image regression task에 대한 비교 결과이다.

4. Novel View Synthesis (NVS)

다음은 NVS 성능을 비교한 결과이다.

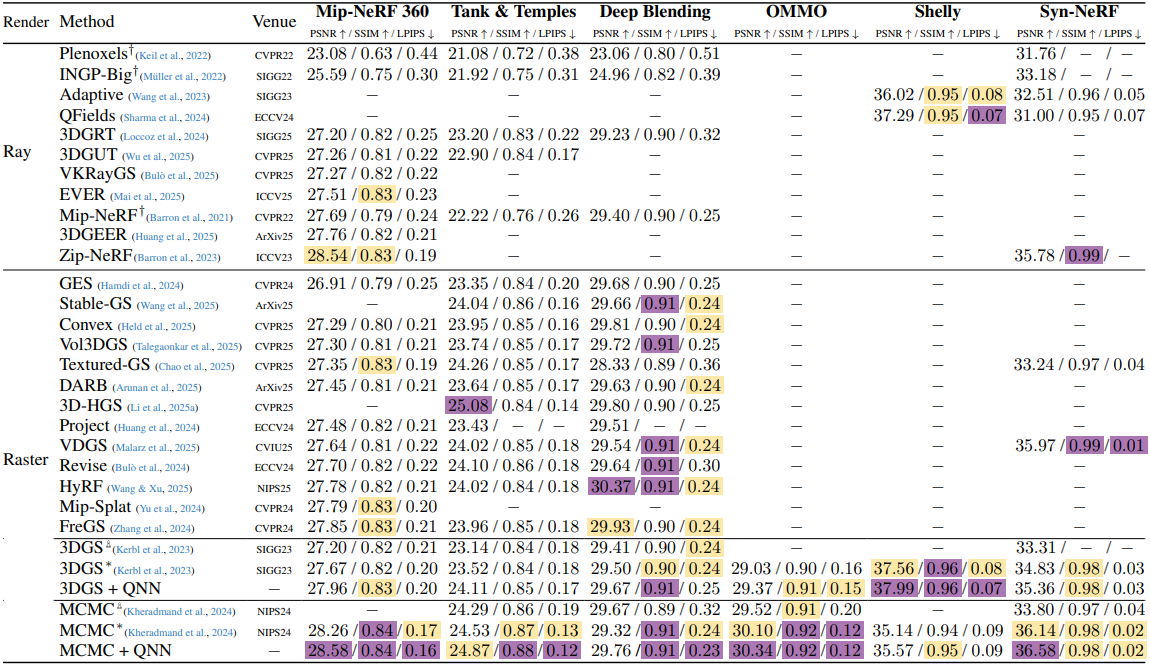
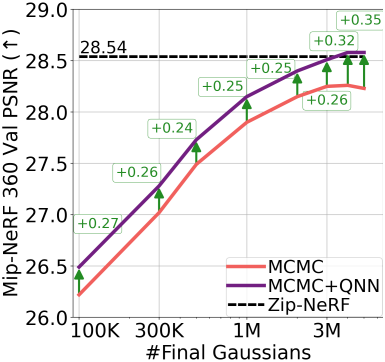
다음은 QNN의 scalability 나타낸 그래프이다. (Mip-NeRF 360)

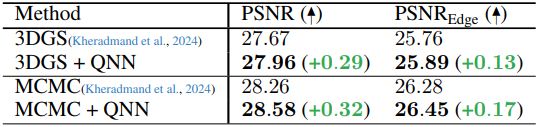
다음은 PSNR_edge를 비교한 결과이다. PSNR_edge는 Canny edge detector로 edge를 식별한 뒤, 커널 크기 3의 disk dilation을 수행하여 계산된다. (Mip-NeRF 360)

j